人教版数学八上12.2 全等三角形的判定 第3课时 “角边角”和“角角边”课件(22张ppt)
文档属性
| 名称 | 人教版数学八上12.2 全等三角形的判定 第3课时 “角边角”和“角角边”课件(22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 14:13:36 | ||
图片预览





文档简介
(共22张PPT)
12.2
全等三角形的判定
第3课时
“角边角”和“角角边
教学目标
1.了解1.探索三角形全等的“角边角”和“角角边”的条件
2.应用“角边角”和“角角边”证明两个三角形全等,进而证线段或角相等.
复习导入
1.能够
的两个三角形叫做全等三角形.
2.判定两个三角形全等方法有哪些?
边边边:
对应相等的两个三角形全等.
边角边:
和它们的
对应相等的两个三角形全等.
2.
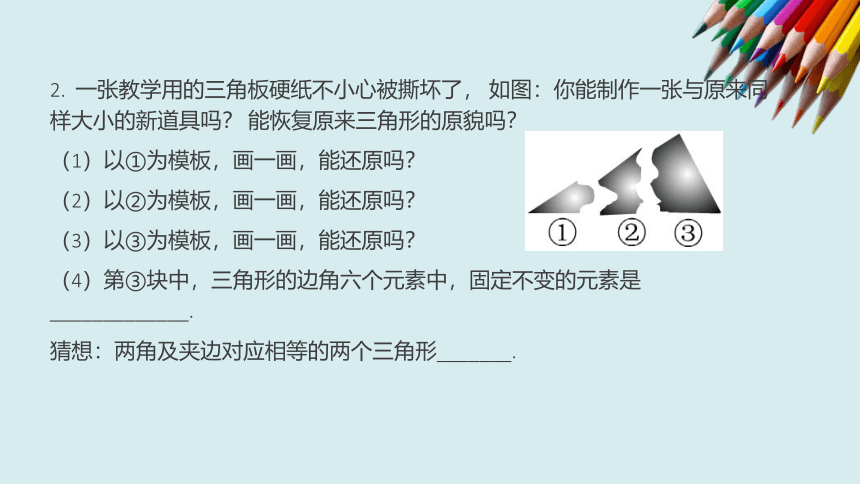
一张教学用的三角板硬纸不小心被撕坏了,
如图:你能制作一张与原来同样大小的新道具吗?
能恢复原来三角形的原貌吗?
(1)以①为模板,画一画,能还原吗?
(2)以②为模板,画一画,能还原吗?
(3)以③为模板,画一画,能还原吗?
(4)第③块中,三角形的边角六个元素中,固定不变的元素是_____________.
猜想:两角及夹边对应相等的两个三角形_______.
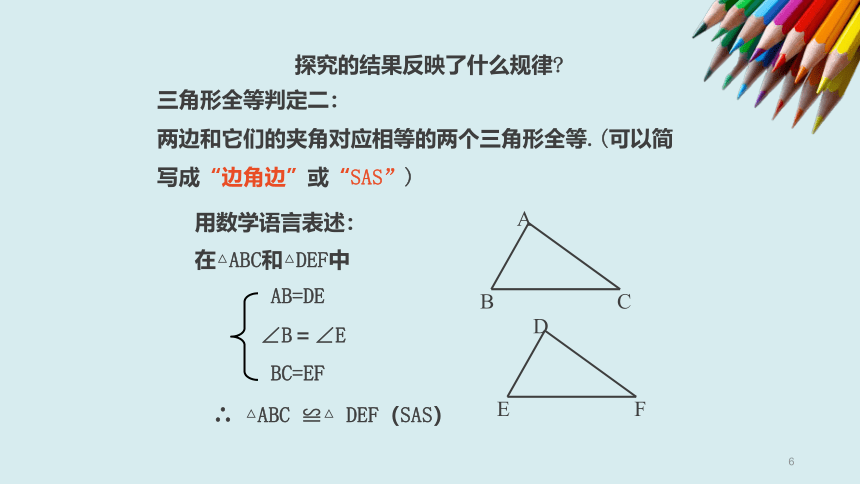
文字语言:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
∠A=∠A′
(已知),
AB=A′
B′
(已知),
∠B=∠B′
(已知),
在△ABC和△A′
B′
C′中,
∴
△ABC≌△
A′
B′
C′
(ASA).
A
B
C
A
′
B
′
C
′
“角边角”判定方法
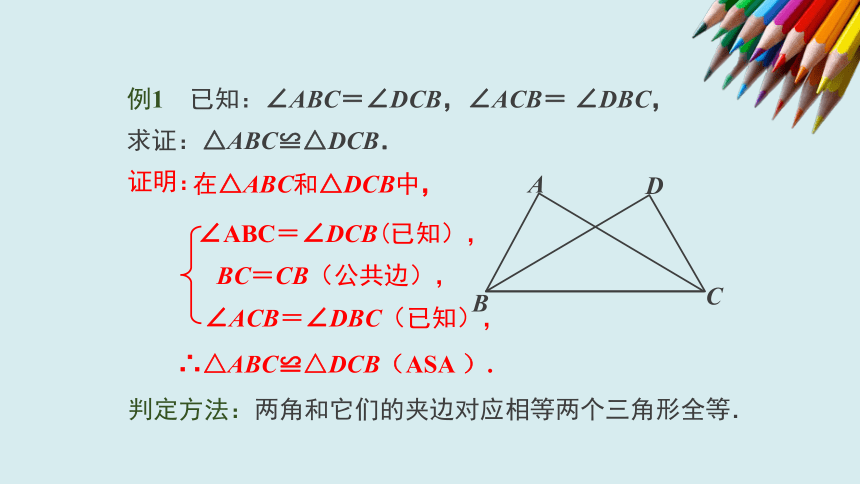
例1
已知:∠ABC=∠DCB,∠ACB=
∠DBC,
求证:△ABC≌△DCB.
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
证明:
在△ABC和△DCB中,
∴△ABC≌△DCB(ASA
).
B
C
A
D
判定方法:两角和它们的夹边对应相等两个三角形全等.
例3:在△ABC和△DEF中,∠A=∠D,∠B=
∠E,BC=EF.求证:△ABC≌△DEF.
∠B=∠E,
BC=EF,
∠C=∠F.
证明:
在△ABC中,∠A+∠B+∠C=180°.
∴△ABC≌△DEF(ASA
).
∴
∠C=180°-∠A-∠B.
同理
∠F=180°-∠D-∠E.
又
∠A=∠D,∠B=
∠E,
∴
∠C=∠F.
在△ABC和△DEF中,
1.
△ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF
,则下列补充的条件中错误的是(
)
A.AC=DF
B.BC=EF
C.∠A=∠D
D.∠C=∠F
2.
在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°
,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A.一定不全等
B.一定全等
C.不一定全等
D.以上都不对
课后练习
A
B
4.已知:如图,
AB⊥BC,AD⊥DC,∠1=∠2,
求证:AB=AD.
A
C
D
B
1
2
证明:
∵
AB⊥BC,AD⊥DC,
∴
∠
B=∠D=90
°.
在△ABC和△ADC中,
∠1=∠2
(已知),
∠
B=∠D(已证),
AC=AC
(公共边),
∴
△ABC≌△ADC(AAS),
∴AB=AD.
5.已知:如图,△ABC
≌△A′B′C′
,AD、A′
D′
分别是△ABC
和△A′B′C′的高.试说明AD=
A′D′
,并用一句话说出你的发现.
A
B
C
D
A
′
B
′
C
′
D
′
解:因为△ABC
≌△A′B′C′
,
所以AB=A'B'(全等三角形对应边相等),∠ABD=∠A'B'D'(全等三角形对应角相等).
因为AD⊥BC,A'D'⊥B'C',所以∠ADB=∠A'D'B'.
在△ABD和△A'B'D'中,
∠ADB=∠A'D'B'(已证),
∠ABD=∠A'B'D'(已证),
AB=AB(已证),
所以△ABD≌△A'B'D'.所以AD=A'D'.
A
B
C
D
A
′
B
′
C
′
D
′
全等三角形对应边上的高也相等.
课堂小结
判定三角形全等的四种方法,它们分别是:
1、边边边(SSS)
3、角边角(ASA)
4、角角边(AAS)
2、边角边(SAS)
12.2
全等三角形的判定
第3课时
“角边角”和“角角边
教学目标
1.了解1.探索三角形全等的“角边角”和“角角边”的条件
2.应用“角边角”和“角角边”证明两个三角形全等,进而证线段或角相等.
复习导入
1.能够
的两个三角形叫做全等三角形.
2.判定两个三角形全等方法有哪些?
边边边:
对应相等的两个三角形全等.
边角边:
和它们的
对应相等的两个三角形全等.
2.
一张教学用的三角板硬纸不小心被撕坏了,
如图:你能制作一张与原来同样大小的新道具吗?
能恢复原来三角形的原貌吗?
(1)以①为模板,画一画,能还原吗?
(2)以②为模板,画一画,能还原吗?
(3)以③为模板,画一画,能还原吗?
(4)第③块中,三角形的边角六个元素中,固定不变的元素是_____________.
猜想:两角及夹边对应相等的两个三角形_______.
文字语言:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
∠A=∠A′
(已知),
AB=A′
B′
(已知),
∠B=∠B′
(已知),
在△ABC和△A′
B′
C′中,
∴
△ABC≌△
A′
B′
C′
(ASA).
A
B
C
A
′
B
′
C
′
“角边角”判定方法
例1
已知:∠ABC=∠DCB,∠ACB=
∠DBC,
求证:△ABC≌△DCB.
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
证明:
在△ABC和△DCB中,
∴△ABC≌△DCB(ASA
).
B
C
A
D
判定方法:两角和它们的夹边对应相等两个三角形全等.
例3:在△ABC和△DEF中,∠A=∠D,∠B=
∠E,BC=EF.求证:△ABC≌△DEF.
∠B=∠E,
BC=EF,
∠C=∠F.
证明:
在△ABC中,∠A+∠B+∠C=180°.
∴△ABC≌△DEF(ASA
).
∴
∠C=180°-∠A-∠B.
同理
∠F=180°-∠D-∠E.
又
∠A=∠D,∠B=
∠E,
∴
∠C=∠F.
在△ABC和△DEF中,
1.
△ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF
,则下列补充的条件中错误的是(
)
A.AC=DF
B.BC=EF
C.∠A=∠D
D.∠C=∠F
2.
在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°
,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A.一定不全等
B.一定全等
C.不一定全等
D.以上都不对
课后练习
A
B
4.已知:如图,
AB⊥BC,AD⊥DC,∠1=∠2,
求证:AB=AD.
A
C
D
B
1
2
证明:
∵
AB⊥BC,AD⊥DC,
∴
∠
B=∠D=90
°.
在△ABC和△ADC中,
∠1=∠2
(已知),
∠
B=∠D(已证),
AC=AC
(公共边),
∴
△ABC≌△ADC(AAS),
∴AB=AD.
5.已知:如图,△ABC
≌△A′B′C′
,AD、A′
D′
分别是△ABC
和△A′B′C′的高.试说明AD=
A′D′
,并用一句话说出你的发现.
A
B
C
D
A
′
B
′
C
′
D
′
解:因为△ABC
≌△A′B′C′
,
所以AB=A'B'(全等三角形对应边相等),∠ABD=∠A'B'D'(全等三角形对应角相等).
因为AD⊥BC,A'D'⊥B'C',所以∠ADB=∠A'D'B'.
在△ABD和△A'B'D'中,
∠ADB=∠A'D'B'(已证),
∠ABD=∠A'B'D'(已证),
AB=AB(已证),
所以△ABD≌△A'B'D'.所以AD=A'D'.
A
B
C
D
A
′
B
′
C
′
D
′
全等三角形对应边上的高也相等.
课堂小结
判定三角形全等的四种方法,它们分别是:
1、边边边(SSS)
3、角边角(ASA)
4、角角边(AAS)
2、边角边(SAS)
