人教版 六年级数学上册3 解决问题(4) 课件(26张PPT)
文档属性
| 名称 | 人教版 六年级数学上册3 解决问题(4) 课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
2.分数除法
六年级数学上册(RJ) 教学课件
3 分数除法
3 分数除法
第7课时 解决问题(4)
1.填一填:
(1)一本书4天看完,平均每天看这本书的( );
(2)一本书每天看 ,那么,看完这本书需要( )天。
5
01
复习导入
2.说说下列问题中的等量关系式:
修一段400米长的公路,一工程队每天修40米,需要几天能修完?
工作效率×工作时间=工作总量
工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
这条道路,
如果我们一队单独修,12天能修完。
如果我们二队单独修,18天才能修完。
如果两队合修,多少天能修完?
02
探究新知
一队单独修_____天能修完;
二队单独修_____天能修完;
要求的是_______________________。
阅读与理解
这条道路到底有多长?我们应该怎么办?
12
18
两队合修多少天能修完
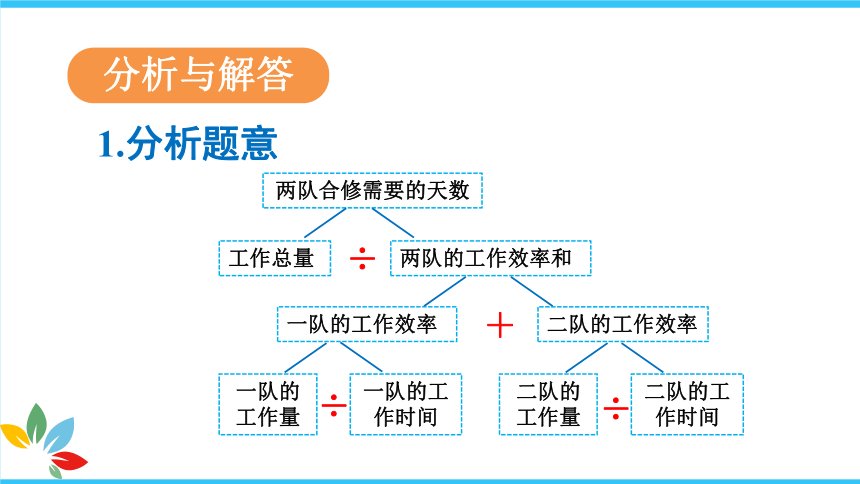
分析与解答
1.分析题意
两队合修需要的天数
两队的工作效率和
工作总量
÷
二队的工作效率
一队的工作效率
+
一队的工作时间
一队的工作量
÷
二队的工作时间
二队的工作量
÷
2.解题思路
根据“工作总量÷工作效率=工作时间”可知:两队合修的天数=这条路的总长度÷两个队每天修的长度和。
如果这条道路的长度已知,那么这个问题就可以直接解答了!
我们可以假设这条道路长18千米、36千米……
3.具体解题方法
方法一:假设这条道路的全长为18千米。
(2)二队每天修的千米数:
分步列式:
(1)一队每天修的千米数:
(3)两队合修,每天修的千米数:
(4)两队合修,需要的天数:
18÷12=1.5(km)
18÷18=1(km)
1.5+1=2.5(km)
18÷2.5=7.2(天)
方法二:假设这条道路的全长为30千米。
(2)二队每天修的千米数:
分步列式:
(1)一队每天修的千米数:
(3)两队合修,每天修的千米数:
(4)两队合修,需要的天数:
方法三:假设这条道路的全长为a千米。
列综合算式为:
方法四:假设这条道路的全长为1。
(2)二队每天修:
分步列式:
(1)一队每天修:
(3)两队合修,每天修:
(4)两队合修,需要的天数:
假设这条道路长18千米
假设这条道路长30千米
假设这条道路是1
你发现了什么?跟同学交流一下!
回顾与反思
怎样才知道以上的解决方法是否正确?
①假设这条道路长18千米,则两队总的工作效率为:
,说明计算结果正确。
②假设这条道路长30千米,则两队总的工作效率为:
,说明计算结果正确。
③假设这条道路长a千米,则两队总的工作效率为:
,说明计算结果正确。
回顾与反思
④假设这条道路长为1,则两队总的工作效率为:
,说明计算结果正确。
答:如果两队合修, 天能修完。
不管假设这条道路有多长,答案都是相同的。把道路长度假设成1更简便。
1.如果两辆车一起运,多少次能运完这批货物?(教材P43“做一做”)
【分析】
若把这批货物看作“1”,则两车的工作效率分别为 。
每次运货物的
每次运货物的
03
学以致用
=2(次)
解:由“工作时间=工作总量÷工作效率”得
答:两辆车一起运,2次能运完这批货物。
2.挖一条水渠,王伯伯每天挖整条水渠的 ,李叔叔每天挖整条水渠的 。两人合作,几天能挖完?(教材P45“练习九”第6题)
=12(天)
答:两人合作,12天能挖完。
3.甲车从A城市到B城市要行驶2小时,乙车从B城市到A城市要行驶3小时。两车同时分别从A城市和B城市出发,几小时后相遇?
(教材P45“练习九”第7题)
甲车:
要行驶2小时
乙车:
要行驶3小时
相 遇
几小时后相遇?
把总路程看成“1”
A城市
B城市
每小时行驶全程的
每小时行驶全程的
解:由“行驶时间=总路程÷速度和”得
(小时)
答:两车同时分别从A城市和B城市出发, 小时后相遇。
4.现在两队合种,5天能种完吗?
(教材P45“练习九”第9题)
每天的工作量是
每天的工作量是
把总数看成“1”
解:由“工作时间=工作总量÷工作效率”得
(天)
答:两队合种,5天能种完。
用分数除法解决工程类实际问题
用分数除法解决工程类实际问题的方法与用整数解决工程类实际问题的解题方法相同,所用的数量关系式也相同:“工作效率×工作时间=工作总量”、“工作总量÷工作效率=工作时间”、“工作总量÷工作时间=工作效率”。
用分数解决工程类实际问题时,把工作总量假设成“1”,用单位时间内完成工作总量的几分之一来表示工作效率。
04
课堂小结
2.分数除法
六年级数学上册(RJ) 教学课件
3 分数除法
3 分数除法
第7课时 解决问题(4)
1.填一填:
(1)一本书4天看完,平均每天看这本书的( );
(2)一本书每天看 ,那么,看完这本书需要( )天。
5
01
复习导入
2.说说下列问题中的等量关系式:
修一段400米长的公路,一工程队每天修40米,需要几天能修完?
工作效率×工作时间=工作总量
工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
这条道路,
如果我们一队单独修,12天能修完。
如果我们二队单独修,18天才能修完。
如果两队合修,多少天能修完?
02
探究新知
一队单独修_____天能修完;
二队单独修_____天能修完;
要求的是_______________________。
阅读与理解
这条道路到底有多长?我们应该怎么办?
12
18
两队合修多少天能修完
分析与解答
1.分析题意
两队合修需要的天数
两队的工作效率和
工作总量
÷
二队的工作效率
一队的工作效率
+
一队的工作时间
一队的工作量
÷
二队的工作时间
二队的工作量
÷
2.解题思路
根据“工作总量÷工作效率=工作时间”可知:两队合修的天数=这条路的总长度÷两个队每天修的长度和。
如果这条道路的长度已知,那么这个问题就可以直接解答了!
我们可以假设这条道路长18千米、36千米……
3.具体解题方法
方法一:假设这条道路的全长为18千米。
(2)二队每天修的千米数:
分步列式:
(1)一队每天修的千米数:
(3)两队合修,每天修的千米数:
(4)两队合修,需要的天数:
18÷12=1.5(km)
18÷18=1(km)
1.5+1=2.5(km)
18÷2.5=7.2(天)
方法二:假设这条道路的全长为30千米。
(2)二队每天修的千米数:
分步列式:
(1)一队每天修的千米数:
(3)两队合修,每天修的千米数:
(4)两队合修,需要的天数:
方法三:假设这条道路的全长为a千米。
列综合算式为:
方法四:假设这条道路的全长为1。
(2)二队每天修:
分步列式:
(1)一队每天修:
(3)两队合修,每天修:
(4)两队合修,需要的天数:
假设这条道路长18千米
假设这条道路长30千米
假设这条道路是1
你发现了什么?跟同学交流一下!
回顾与反思
怎样才知道以上的解决方法是否正确?
①假设这条道路长18千米,则两队总的工作效率为:
,说明计算结果正确。
②假设这条道路长30千米,则两队总的工作效率为:
,说明计算结果正确。
③假设这条道路长a千米,则两队总的工作效率为:
,说明计算结果正确。
回顾与反思
④假设这条道路长为1,则两队总的工作效率为:
,说明计算结果正确。
答:如果两队合修, 天能修完。
不管假设这条道路有多长,答案都是相同的。把道路长度假设成1更简便。
1.如果两辆车一起运,多少次能运完这批货物?(教材P43“做一做”)
【分析】
若把这批货物看作“1”,则两车的工作效率分别为 。
每次运货物的
每次运货物的
03
学以致用
=2(次)
解:由“工作时间=工作总量÷工作效率”得
答:两辆车一起运,2次能运完这批货物。
2.挖一条水渠,王伯伯每天挖整条水渠的 ,李叔叔每天挖整条水渠的 。两人合作,几天能挖完?(教材P45“练习九”第6题)
=12(天)
答:两人合作,12天能挖完。
3.甲车从A城市到B城市要行驶2小时,乙车从B城市到A城市要行驶3小时。两车同时分别从A城市和B城市出发,几小时后相遇?
(教材P45“练习九”第7题)
甲车:
要行驶2小时
乙车:
要行驶3小时
相 遇
几小时后相遇?
把总路程看成“1”
A城市
B城市
每小时行驶全程的
每小时行驶全程的
解:由“行驶时间=总路程÷速度和”得
(小时)
答:两车同时分别从A城市和B城市出发, 小时后相遇。
4.现在两队合种,5天能种完吗?
(教材P45“练习九”第9题)
每天的工作量是
每天的工作量是
把总数看成“1”
解:由“工作时间=工作总量÷工作效率”得
(天)
答:两队合种,5天能种完。
用分数除法解决工程类实际问题
用分数除法解决工程类实际问题的方法与用整数解决工程类实际问题的解题方法相同,所用的数量关系式也相同:“工作效率×工作时间=工作总量”、“工作总量÷工作效率=工作时间”、“工作总量÷工作时间=工作效率”。
用分数解决工程类实际问题时,把工作总量假设成“1”,用单位时间内完成工作总量的几分之一来表示工作效率。
04
课堂小结
