人教版 六年级数学上册3分数除法整理和复习 课件(29张PPT)
文档属性
| 名称 | 人教版 六年级数学上册3分数除法整理和复习 课件(29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
整理和复习
六年级数学上册(RJ) 教学课件
3 分数除法
3 分数除法
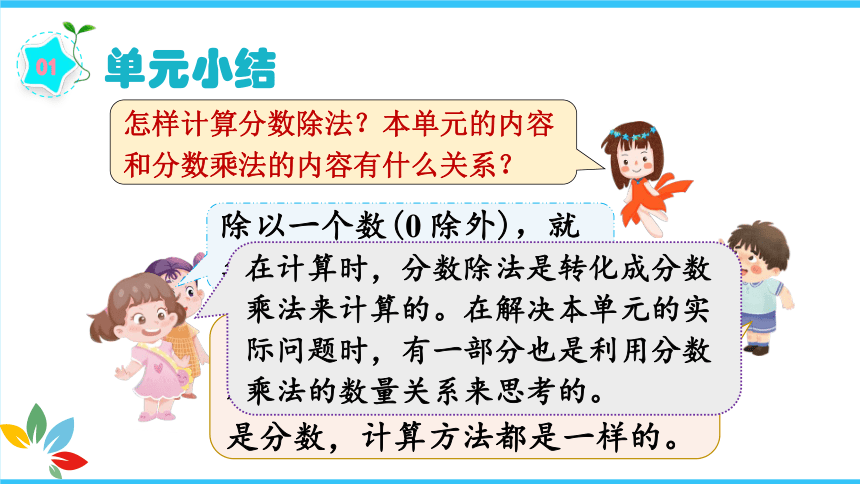
怎样计算分数除法?本单元的内容和分数乘法的内容有什么关系?
除以一个数(0 除外),就等于乘这个数的倒数。
整数可以看成分母是1的分数,所以不管被除数、除数是整数还是分数,计算方法都是一样的。
在计算时,分数除法是转化成分数乘法来计算的。在解决本单元的实际问题时,有一部分也是利用分数乘法的数量关系来思考的。
01
单元小结
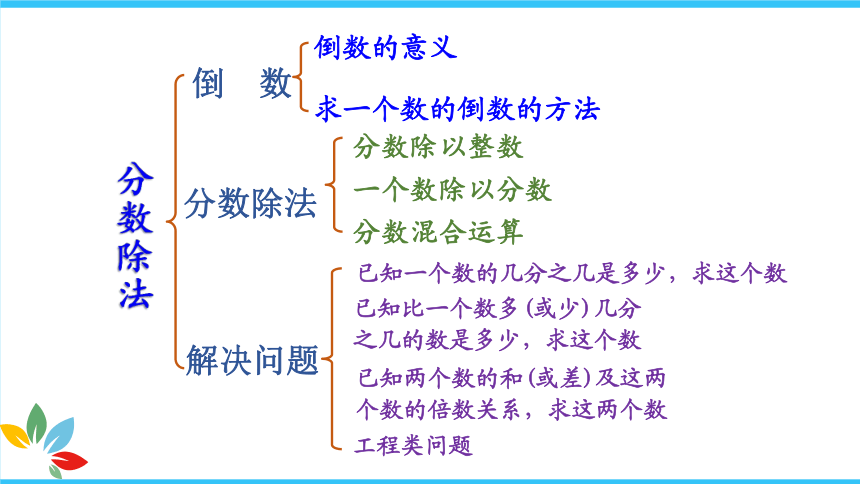
已知一个数的几分之几是多少,求这个数
已知比一个数多(或少)几分之几的数是多少,求这个数
工程类问题
分数除法
倒 数
解决问题
倒数的意义
求一个数的倒数的方法
分数除以整数
分数除法
一个数除以分数
分数混合运算
已知两个数的和(或差)及这两个数的倍数关系,求这两个数
乘积是1的两个数互为倒数。求一个数的倒数就是交换分子和分母的位置(1的倒数是1,0没有倒数)。
倒数的认识
的倒数是_____;
的倒数是_____;
1的倒数是_____;
0没有倒数。
1
02
知识梳理
一个数(可以是整数、分数,也可以是小数)除以一个不等于0的分数,等于这个数乘以分数的倒数。
分数除法
分数四则混合运算顺序
1.分数四则混合运算的顺序和整数四则混合运算的顺序相同。
3.有括号的,先算括号里面的,再算括号外面的。
2.在没有括号的算式里,先算乘除后算加减,从左到右依次计算。
用分数除法解决问题
1
已知一个数的几分之几是多少,求这个数
(1)方程法:
找出单位“1”的量(未知)→找出题中的等量关系→设单位为“1”的量为x,列出方程并解答;
(2)算术法:
找出单位“1”的量(未知)→用“已知量÷已知量占单位“1”的几分之几”。
2
已知比一个数多(或少)几分之几的数是多少,求这个数
根据题中的等量关系“单位‘1’的量×(1±几分之几)=已知量”或“单位‘1’的量±单位‘1’的量×几分之几=已知量”,设单位“1”的量为x,列方程解答。
3
已知两个数的和(或差)及这两个数的倍数关系,求这两个数
(1)设其中一个数为x,根据两个数的倍数关系,用含有未知数x 的式子表示另外一个数;
(2)根据“两个数的和(或差)等于已知量”列方程;
(3)解方程求出x的值,根据两个数的关系求出另外一个数。
4
用分数除法解决工程类问题
用分数除法解决工程类实际问题的方法与用整数解决工程类实际问题的解题方法相同,所用的数量关系式也相同:“工作效率×工作时间=工作总量”、“工作总量÷工作效率=工作时间”、“工作总量÷工作时间=工作效率”。
用分数解决工程类实际问题时,把工作总量假设成“1”,用单位时间内完成工作总量的几分之一来表示工作效率。
1.计算下面各题。(教材P46“整理和复习”第1题)
03
综合训练
2.(1)张大爷养了200只鹅,鹅的只数是鸭的 。养了多少只鸭?
(教材P46“整理和复习”第2题)
200只鹅
鹅的只数是鸭的
养了?只鸭
解:设养了x只鸭。由题意,得
答:养了500只鸭。
200只鹅
鹅的只数是鸭的
养了?只鸭
(2)张大爷养了200只鹅,鹅的只数比鸭少
。养了多少只鸭?
?只
鹅
鸭
鹅的只数比鸭少 ,表示鹅的只数只有鸭的只数的 。
200只
鹅的只数比鸭少
解:设养了y只鸭。由题意,得
答:养了500只鸭。
?只
鹅
鸭
200只
鹅的只数比鸭少
(3)张大爷养的鹅和鸭共有700只,其中鹅的只数是鸭的 。鹅和鸭各有多少只?
【分析】题目中的等量关系式有:
鹅的只数+鸭的只数=700只
鹅的只数=鸭的只数×
m=500
解:设鸭有m只,则鹅有 只。
由题意,得
鹅的只数是 (只)。
答:鸭有500只,则鹅有200只。
3.判断对错,对的画“√”,错的画“×”。
(教材P47“练习十”第1题)
(1)两个分数相除,商一定大于被除数。 ( )
(2)如果 ,b就是a的3倍。 ( )
(3)如果 ,那么a=3,b=5。 ( )
×
√
×
(1)当除数是假分数时,如 ,商小于被除数。
(3)当a=6,b=10时,如 。
4.冰融化成水后,水的体积是冰的体积的 。现有一块冰,融化成水以后的体积是27dm3,这块冰的体积是多少立方分米?
(教材P47“练习十”第3题)
?立方分米
水的体积
冰的体积
27dm3
水的体积是冰的体积的
解:设这块冰的体积是x立方分米。由题意,得
答:这块冰的体积是30立方分米。
?立方分米
水的体积
冰的体积
27dm3
水的体积是冰的体积的
单独的一个数不能成为倒数,倒数是相互依存的一对数。
【错解分析】
倒数是相互依存的,不能单独的说某个数是倒数,因此这句话是错误的,应该说
互为倒数。
04
易错辨析
判断: 是倒数, 也是倒数。 ( )
1
√
下列关于 的计算,正确的是( C )
2
B.
A.
C.
【错解分析】
此题错在没有掌握分数除法的计算方法。A选项错在用分数的分母除以整数了;C选项错在将被除数的分子、分母互换了位置。所以此题的正解为B选项。
分数除以一个不等于0的整数,等于分数乘以这个数的倒数。
一条水渠长3.3 m,甲单独修要5小时完成,乙单独修要6小时完成。两人合作,几小时可以修完?
3
答:两人合作,9小时可以修完。
【错解分析】
此题错在工作量与工作效率不匹配。根据水渠长3.3 m和甲、乙两人单独修完所用的时间求甲、乙两人的工作效率时,应该是3.3÷5和3.3÷6,而不是 。反过来,如果用 表示甲、乙两人的工作效率,那么所对应的工作总量应该是1。
【正解】
答:两人合作, 小时可以修完。
一条水渠长3.3 m,甲单独修要5小时完成,乙单独修要6小时完成。两人合作,几小时可以修完?
3
本单元结束了,你有什么收获?
1.知道了倒数的概念以及会求一个数的倒数。
2.会计算分数除法。
04
畅所欲言
3.会利用分数除法来解决实际问题。
整理和复习
六年级数学上册(RJ) 教学课件
3 分数除法
3 分数除法
怎样计算分数除法?本单元的内容和分数乘法的内容有什么关系?
除以一个数(0 除外),就等于乘这个数的倒数。
整数可以看成分母是1的分数,所以不管被除数、除数是整数还是分数,计算方法都是一样的。
在计算时,分数除法是转化成分数乘法来计算的。在解决本单元的实际问题时,有一部分也是利用分数乘法的数量关系来思考的。
01
单元小结
已知一个数的几分之几是多少,求这个数
已知比一个数多(或少)几分之几的数是多少,求这个数
工程类问题
分数除法
倒 数
解决问题
倒数的意义
求一个数的倒数的方法
分数除以整数
分数除法
一个数除以分数
分数混合运算
已知两个数的和(或差)及这两个数的倍数关系,求这两个数
乘积是1的两个数互为倒数。求一个数的倒数就是交换分子和分母的位置(1的倒数是1,0没有倒数)。
倒数的认识
的倒数是_____;
的倒数是_____;
1的倒数是_____;
0没有倒数。
1
02
知识梳理
一个数(可以是整数、分数,也可以是小数)除以一个不等于0的分数,等于这个数乘以分数的倒数。
分数除法
分数四则混合运算顺序
1.分数四则混合运算的顺序和整数四则混合运算的顺序相同。
3.有括号的,先算括号里面的,再算括号外面的。
2.在没有括号的算式里,先算乘除后算加减,从左到右依次计算。
用分数除法解决问题
1
已知一个数的几分之几是多少,求这个数
(1)方程法:
找出单位“1”的量(未知)→找出题中的等量关系→设单位为“1”的量为x,列出方程并解答;
(2)算术法:
找出单位“1”的量(未知)→用“已知量÷已知量占单位“1”的几分之几”。
2
已知比一个数多(或少)几分之几的数是多少,求这个数
根据题中的等量关系“单位‘1’的量×(1±几分之几)=已知量”或“单位‘1’的量±单位‘1’的量×几分之几=已知量”,设单位“1”的量为x,列方程解答。
3
已知两个数的和(或差)及这两个数的倍数关系,求这两个数
(1)设其中一个数为x,根据两个数的倍数关系,用含有未知数x 的式子表示另外一个数;
(2)根据“两个数的和(或差)等于已知量”列方程;
(3)解方程求出x的值,根据两个数的关系求出另外一个数。
4
用分数除法解决工程类问题
用分数除法解决工程类实际问题的方法与用整数解决工程类实际问题的解题方法相同,所用的数量关系式也相同:“工作效率×工作时间=工作总量”、“工作总量÷工作效率=工作时间”、“工作总量÷工作时间=工作效率”。
用分数解决工程类实际问题时,把工作总量假设成“1”,用单位时间内完成工作总量的几分之一来表示工作效率。
1.计算下面各题。(教材P46“整理和复习”第1题)
03
综合训练
2.(1)张大爷养了200只鹅,鹅的只数是鸭的 。养了多少只鸭?
(教材P46“整理和复习”第2题)
200只鹅
鹅的只数是鸭的
养了?只鸭
解:设养了x只鸭。由题意,得
答:养了500只鸭。
200只鹅
鹅的只数是鸭的
养了?只鸭
(2)张大爷养了200只鹅,鹅的只数比鸭少
。养了多少只鸭?
?只
鹅
鸭
鹅的只数比鸭少 ,表示鹅的只数只有鸭的只数的 。
200只
鹅的只数比鸭少
解:设养了y只鸭。由题意,得
答:养了500只鸭。
?只
鹅
鸭
200只
鹅的只数比鸭少
(3)张大爷养的鹅和鸭共有700只,其中鹅的只数是鸭的 。鹅和鸭各有多少只?
【分析】题目中的等量关系式有:
鹅的只数+鸭的只数=700只
鹅的只数=鸭的只数×
m=500
解:设鸭有m只,则鹅有 只。
由题意,得
鹅的只数是 (只)。
答:鸭有500只,则鹅有200只。
3.判断对错,对的画“√”,错的画“×”。
(教材P47“练习十”第1题)
(1)两个分数相除,商一定大于被除数。 ( )
(2)如果 ,b就是a的3倍。 ( )
(3)如果 ,那么a=3,b=5。 ( )
×
√
×
(1)当除数是假分数时,如 ,商小于被除数。
(3)当a=6,b=10时,如 。
4.冰融化成水后,水的体积是冰的体积的 。现有一块冰,融化成水以后的体积是27dm3,这块冰的体积是多少立方分米?
(教材P47“练习十”第3题)
?立方分米
水的体积
冰的体积
27dm3
水的体积是冰的体积的
解:设这块冰的体积是x立方分米。由题意,得
答:这块冰的体积是30立方分米。
?立方分米
水的体积
冰的体积
27dm3
水的体积是冰的体积的
单独的一个数不能成为倒数,倒数是相互依存的一对数。
【错解分析】
倒数是相互依存的,不能单独的说某个数是倒数,因此这句话是错误的,应该说
互为倒数。
04
易错辨析
判断: 是倒数, 也是倒数。 ( )
1
√
下列关于 的计算,正确的是( C )
2
B.
A.
C.
【错解分析】
此题错在没有掌握分数除法的计算方法。A选项错在用分数的分母除以整数了;C选项错在将被除数的分子、分母互换了位置。所以此题的正解为B选项。
分数除以一个不等于0的整数,等于分数乘以这个数的倒数。
一条水渠长3.3 m,甲单独修要5小时完成,乙单独修要6小时完成。两人合作,几小时可以修完?
3
答:两人合作,9小时可以修完。
【错解分析】
此题错在工作量与工作效率不匹配。根据水渠长3.3 m和甲、乙两人单独修完所用的时间求甲、乙两人的工作效率时,应该是3.3÷5和3.3÷6,而不是 。反过来,如果用 表示甲、乙两人的工作效率,那么所对应的工作总量应该是1。
【正解】
答:两人合作, 小时可以修完。
一条水渠长3.3 m,甲单独修要5小时完成,乙单独修要6小时完成。两人合作,几小时可以修完?
3
本单元结束了,你有什么收获?
1.知道了倒数的概念以及会求一个数的倒数。
2.会计算分数除法。
04
畅所欲言
3.会利用分数除法来解决实际问题。
