22.3 实际问题与二次函数 同步训练 2021-2022学年人教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 22.3 实际问题与二次函数 同步训练 2021-2022学年人教版九年级数学上册(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 464.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 18:27:11 | ||
图片预览




文档简介
人教版
九年级数学上册
22.3
实际问题与二次函数
同步训练
一、选择题
1.
某种服装的销售利润y(万元)与销售数量x(万件)之间满足函数解析式y=-2x2+4x+5,则利润的( )
A.最大值为5万元
B.最大值为7万元
C.最小值为5万元
D.最小值为7万元
2.
某企业生产季节性产品,当产品无利润时,企业自动停产,经过调研,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=-n2+12n-11,则企业停产的月份为( )
A.1月和11月
B.1月、11月和12月
C.1月
D.1月至11月
3.
某广场有一喷水池,水从地面喷出,以水平地面为x轴,出水点为原点,建立如图所示的平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米
B.3米
C.2米
D.1米
4.
如图,利用一个直角墙角修建一个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD的总长为12
m,则该梯形储料场ABCD的最大面积是( )
A.18
m2
B.18
m2
C.24
m2
D.
m2
5.
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.有下列结论:
①小球在空中经过的路程是40
m;②小球抛出3秒后,速度越来越快;
③小球抛出3秒时速度为0;④小球的高度h=30
m时,t=1.5
s.
其中正确的是( )
A.①④
B.①②
C.②③④
D.②③
6.
如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数解析式是y=-x2+x+,则该运动员此次掷铅球的成绩是( )
A.6
m
B.12
m
C.8
m
D.10
m
7.
如图,在△ABC中,∠C=90°,AB=10
cm,BC=8
cm,点P从点A沿AC向点C以1
cm/s的速度运动,同时点Q从点C沿CB向点B以2
cm/s的速度运动(点Q运动到点B时,两点同时停止运动),在运动过程中,四边形PABQ的面积的最小值为
( )
A.19
cm2
B.16
cm2
C.15
cm2
D.12
cm2
8.
在羽毛球比赛中,羽毛球的运动路线可以看作是抛物线y=-x2+bx+c的一部分(如图),其中出球点B离地面点O的距离是1
m,球落地点A到点O的距离是4
m,那么这条抛物线的解析式是( )
A.y=-x2+x+1
B.y=-x2+x-1
C.y=-x2-x+1
D.y=-x2-x-1
二、填空题
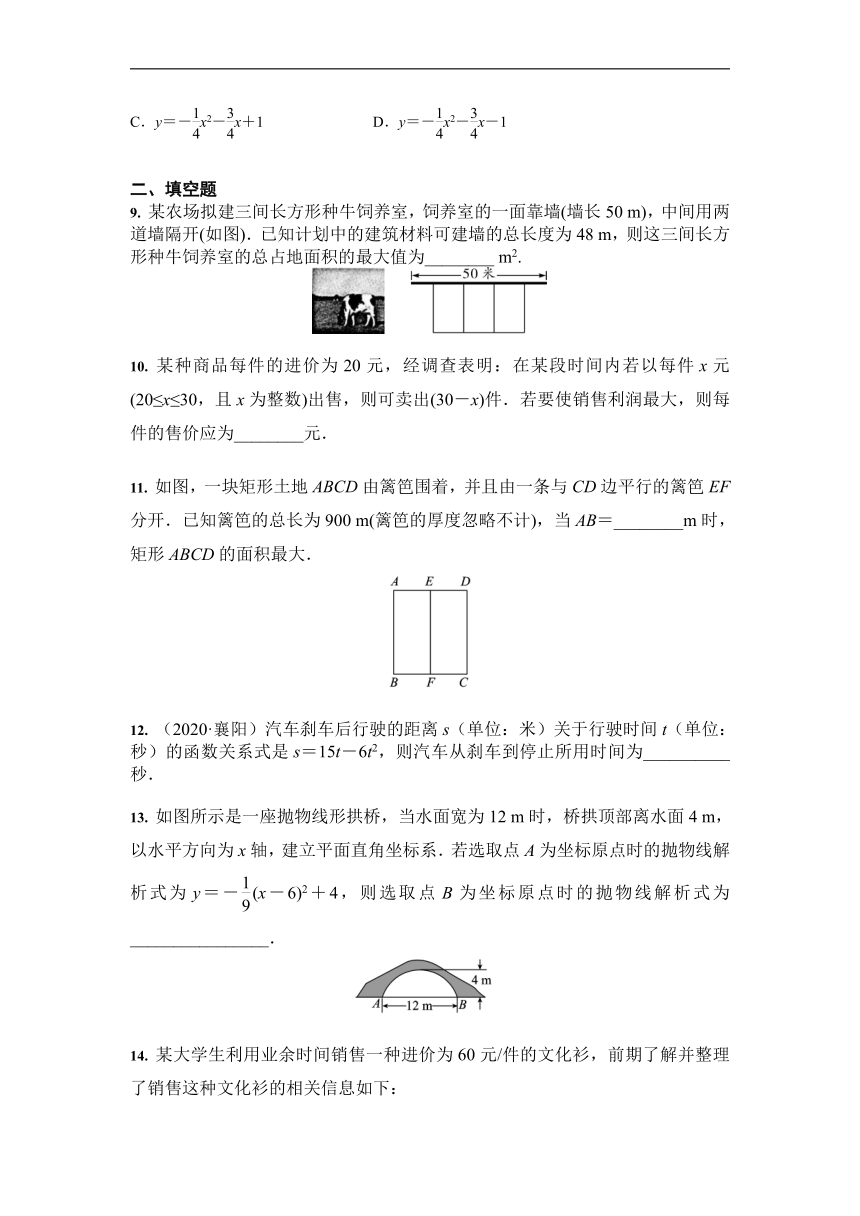
9.
某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长50
m),中间用两道墙隔开(如图).已知计划中的建筑材料可建墙的总长度为48
m,则这三间长方形种牛饲养室的总占地面积的最大值为________
m2.
10.
某种商品每件的进价为20元,经调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,则可卖出(30-x)件.若要使销售利润最大,则每件的售价应为________元.
11.
如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900
m(篱笆的厚度忽略不计),当AB=________m时,矩形ABCD的面积最大.
12.
(2020·襄阳)汽车刹车后行驶的距离s(单位:米)关于行驶时间t(单位:秒)的函数关系式是s=15t-6t2,则汽车从刹车到停止所用时间为__________秒.
13.
如图所示是一座抛物线形拱桥,当水面宽为12
m时,桥拱顶部离水面4
m,以水平方向为x轴,建立平面直角坐标系.若选取点A为坐标原点时的抛物线解析式为y=-(x-6)2+4,则选取点B为坐标原点时的抛物线解析式为________________.
14.
某大学生利用业余时间销售一种进价为60元/件的文化衫,前期了解并整理了销售这种文化衫的相关信息如下:
(1)月销量y(件)与售价x(元/件)的关系满足y=-2x+400;
(2)工商部门限制售价x满足70≤x≤150(计算月利润时不考虑其他成本).
给出下列结论:
①这种文化衫的月销量最小为100件;
②这种文化衫的月销量最大为260件;
③销售这种文化衫的月利润最小为2600元;
④销售这种文化衫的月利润最大为9000元.
其中正确的是________.(把所有正确结论的序号都填上)
15.
某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t·
为正整数)的增大而增大,a的取值范围应为________.
16.
竖直上抛的小球离地高度是它运动时间的二次函数.小军相隔1秒依次竖直向上抛出两个小球.假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度.第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t=________.
三、解答题
17.
旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的运营规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入-管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
18.
已知一条双向公路隧道,其横断面由抛物线和矩形ABCD的三边组成,隧道的最大高度为4.9米,AB=10米,BC=2.4米,现把隧道横断面放在如图所示的平面直角坐标系中,有一辆高为4米,宽为2米的装有集装箱的汽车要通过该隧道,如果不考虑其他因素,汽车的右侧至少离开隧道石壁多少米才不至于碰到隧道顶部?
19.
(2019?湘潭)某政府工作报告中强调,2019年着重推进乡村振兴战略,做优做响湘莲等特色农产品品牌.小亮调查了一家湘潭特产店两种湘莲礼盒一个月的销售情况,A种湘莲礼盒进价72元/盒,售价120元/盒,B种湘莲礼盒进价40元/盒,售价80元/盒,这两种湘莲礼盒这个月平均每天的销售总额为2800元,平均每天的总利润为1280元.
(1)求该店平均每天销售这两种湘莲礼盒各多少盒?
(2)小亮调査发现,种湘莲礼盒售价每降3元可多卖1盒.若种湘莲礼盒的售价和销量不变,当种湘莲礼盒降价多少元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是多少元?
20.
如图,排球运动员王亮站在点O处练习发球,将球从点O正上方2
m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与点O的水平距离为9
m,高度为2.43
m,球场的边界距点O的水平距离为18
m.
(1)当h=2.6时,
①求y关于x的函数解析式(不要求写出自变量x的取值范围);
②球能否越过球网?球会不会出界?请说明理由;
③若排球运动员张明站在另外半场的点M(m,0),且张明原地起跳接球的最大高度为2.4
m.若张明因接球的高度不够而失球,求m的取值范围.
(2)若球一定能越过球网,又不出边界,求h的取值范围.
人教版
九年级数学上册
22.3
实际问题与二次函数
同步训练-答案
一、选择题
1.
【答案】B
2.
【答案】B [解析]
由题意知,利润y和月份n之间的函数关系式为y=-n2+12n-11,
∴y=-(n-6)2+25,
当n=1时,y=0;
当n=11时,y=0;
当n=12时,y<0.
故停产的月份是1月、11月和12月.
故选B.
3.
【答案】A [解析]
y=-(x2-4x+4)+4=-(x-2)2+4,∴水喷出的最大高度是4米.
4.
【答案】C [解析]
如图,过点C作CE⊥AB于点E,
则四边形ADCE为矩形,∠DCE=∠CEB=90°,
则∠BCE=∠BCD-∠DCE=30°.
设CD=AE=x
m,则BC=(12-x)m.
在Rt△CBE中,∵∠CEB=90°,∠BCE=30°,
∴BE=BC=(6-x)m,
∴AD=CE==(6
-x)m,AB=AE+BE=x+6-x=(x+6)m,
∴梯形ABCD的面积=(CD+AB)·CE
=(x+x+6)·(6
-x)
=-x2+3
x+18
=-(x-4)2+24
.
∴当x=4时,S最大=24
.
即CD的长为4
m时,梯形储料场ABCD的面积最大为24
m2.故选C.
5.
【答案】D [解析]
①由图象知小球在空中达到的最大高度是40
m,故①错误;
②小球抛出3秒后,速度越来越快,故②正确;
③∵小球抛出3秒时达到最高点,∴速度为0,故③正确;
④设函数解析式为h=a(t-3)2+40,
把O(0,0)代入得0=a(0-3)2+40.
解得a=-,
∴函数解析式为h=-(t-3)2+40.
把h=30代入解析式,得30=-(t-3)2+40,
解得t=4.5或t=1.5,
∴小球的高度h=30
m时,t=1.5
s或4.5
s,故④错误.故选D.
6.
【答案】D [解析]
把y=0代入y=-x2+x+,得-x2+x+=0,
解得x1=10,x2=-2.又∵x>0,∴x=10.
故选D.
7.
【答案】C [解析]
在Rt△ABC中,∠C=90°,AB=10
cm,BC=8
cm,
∴AC==6
cm.
设运动时间为t
s(0cm,
∴S四边形PABQ=S△ABC-S△CPQ=AC·BC-PC·CQ=×6×8-(6-t)×2t=t2-6t+24=(t-3)2+15,
∴当t=3时,四边形PABQ的面积取得最小值,最小值为15
cm2.
故选C.
8.
【答案】A [解析]
A,B两点的坐标分别为(4,0),(0,1),把(4,0),(0,1)分别代入y=-x2+bx+c,求出b,c的值即可.
二、填空题
9.
【答案】144 【解析】∵围墙的总长为50
m,设3间饲养室合计长x
m,则饲养室的宽=
m,∴总占地面积为y=x·=-x2+12x(0<x<48),由y=-x2+12x=-(x-24)2+144,∵x=24在0<x<48范围内,a=-<0,∴在0<x≤24范围内,y随x的增大而增大,∴x=24时,y取得最大值,y最大=144
m2.
10.
【答案】25 [解析]
设利润为w元,则w=(x-20)(30-x)=-(x-25)2+25.
∵20≤x≤30,
∴当x=25时,二次函数有最大值25.
11.
【答案】150 [解析]
设AB=x
m,则AB=EF=CD=x
m,所以AD=BC=(900-3x)m.设矩形ABCD的面积为y
m2,则y=x·(900-3x)=-x2+450x(0<x<300).由于二次项系数小于0,所以y有最大值,且当x=-=-=150时,函数y取得最大值.
故当AB=150
m矩形ABCD的面积最大.
12.
【答案】2.5.
【解析】令s=0,得15t-6t2=0,解得t1=2.5,t2=0(不合题意,舍去),故答案为2.5.
13.
【答案】y=-(x+6)2+4
14.
【答案】①②③ [解析]
由题意知,当70≤x≤150时,y=-2x+400,
∵-2<0,∴y随x的增大而减小,
∴当x=150时,y取得最小值,最小值为100,故①正确;
当x=70时,y取得最大值,最大值为260,故②正确;
设销售这种文化衫的月利润为W元,
则W=(x-60)(-2x+400)=-2(x-130)2+9800,
∵70≤x≤150,
∴当x=70时,W取得最小值,最小值为-2(70-130)2+9800=2600,故③正确;
当x=130时,W取得最大值,最大值为9800,故④错误.
故答案为①②③.
15.
【答案】016.
【答案】1.6
秒 【解析】本题主要考查了二次函数的对称性问题.由题意可知,各自抛出后1.1秒时到达相同最大离地高度,即到达二次函数图象的顶点处,故此二次函数图象的对称轴为t=1.1;由于两次抛小球的时间间隔为1秒,所以当第一个小球和第二个小球到达相同高度时,则这两个小球必分居对称轴左右两侧,由于高度相同,则在该时间节点上,两小球对应时间到对称轴距离相同.
故该距离为0.5秒,
所以此时第一个小球抛出后t=1.1+0.5=1.6秒时与第二个小球的离地高度相同.
三、解答题
17.
【答案】
解:(1)由题意知,若观光车能全部租出,则0由50x-1100>0,(2分)
解得x>22,(3分)
又∵x是5的倍数,
∴每辆车的日租金至少应为25元.(5分)
(2)设每天的净收入为y元,
当0∵y1随x的增大而增大,
∴当x=100时,y1的最大值为50×100-1100=3900;(8分)
当x>100时,y2=(50-)x-1100=-x2+70x-1100=-(x-175)2+5025.(9分)
∴当x=175时,y2的最大值是5025,
∵5025>3900,
∴当每辆车的日租金为175元时,每天的净收入最多是5025元.(10分)
18.
【答案】
解:由题意,知AB=10米,BC=2.4米,
∴C(10,0),B(10,-2.4),A(0,-2.4).
由题意,知抛物线的顶点坐标为(5,2.5).
设抛物线的解析式为y=a(x-5)2+2.5.
将(10,0)代入解析式,
得0=a(10-5)2+2.5,
解得a=-,
∴y=-(x-5)2+2.5=-x2+x.
此公路为双向公路,当汽车高为4米时,在抛物线隧道中对应的纵坐标y=4-2.4=1.6,
由1.6=-x2+x,
解得x1=2,x2=8.
故汽车要通过隧道,其右侧至少要离开隧道石壁2米才不至于碰到隧道顶部.
19.
【答案】
(1)根据题意,可设平均每天销售礼盒盒,种礼盒为盒,
则有,解得,
故该店平均每天销售礼盒10盒,种礼盒为20盒.
(2)设A种湘莲礼盒降价元/盒,利润为元,依题意
总利润,
化简得,
∵,
∴当时,取得最大值为1307,
故当种湘莲礼盒降价9元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是1307元.
20.
【答案】
解:(1)①把x=0,y=2及h=2.6代入y=a(x-6)2+h,得2=a(0-6)2+2.6,
∴a=-,
∴y=-(x-6)2+2.6.
②球能越过球网,球会出界.理由如下:
由①知y=-(x-6)2+2.6,
当x=9时,y=-×(9-6)2+2.6=2.45>2.43,
∴球能越过球网.
当x=18时,y=-×(18-6)2+2.6=0.2>0,∴球会出界.
③若运动员张明原地起跳到最大高度时刚好接到球,此时-(m-6)2+2.6=2.4,
解得m1=6+2
,m2=6-2
.
∵张明接球高度不够,∴6-2
<m<6+2
.∵张明在另外半场,
∴m的取值范围为9<m<6+2
.
(2)将x=0,y=2代入y=a(x-6)2+h,得a=.
当x=9时,y=(9-6)2+h=>2.43;①
当x=18时,y=(18-6)2+h=8-3h≤0.②
由①②,得h≥.
九年级数学上册
22.3
实际问题与二次函数
同步训练
一、选择题
1.
某种服装的销售利润y(万元)与销售数量x(万件)之间满足函数解析式y=-2x2+4x+5,则利润的( )
A.最大值为5万元
B.最大值为7万元
C.最小值为5万元
D.最小值为7万元
2.
某企业生产季节性产品,当产品无利润时,企业自动停产,经过调研,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=-n2+12n-11,则企业停产的月份为( )
A.1月和11月
B.1月、11月和12月
C.1月
D.1月至11月
3.
某广场有一喷水池,水从地面喷出,以水平地面为x轴,出水点为原点,建立如图所示的平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米
B.3米
C.2米
D.1米
4.
如图,利用一个直角墙角修建一个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD的总长为12
m,则该梯形储料场ABCD的最大面积是( )
A.18
m2
B.18
m2
C.24
m2
D.
m2
5.
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.有下列结论:
①小球在空中经过的路程是40
m;②小球抛出3秒后,速度越来越快;
③小球抛出3秒时速度为0;④小球的高度h=30
m时,t=1.5
s.
其中正确的是( )
A.①④
B.①②
C.②③④
D.②③
6.
如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数解析式是y=-x2+x+,则该运动员此次掷铅球的成绩是( )
A.6
m
B.12
m
C.8
m
D.10
m
7.
如图,在△ABC中,∠C=90°,AB=10
cm,BC=8
cm,点P从点A沿AC向点C以1
cm/s的速度运动,同时点Q从点C沿CB向点B以2
cm/s的速度运动(点Q运动到点B时,两点同时停止运动),在运动过程中,四边形PABQ的面积的最小值为
( )
A.19
cm2
B.16
cm2
C.15
cm2
D.12
cm2
8.
在羽毛球比赛中,羽毛球的运动路线可以看作是抛物线y=-x2+bx+c的一部分(如图),其中出球点B离地面点O的距离是1
m,球落地点A到点O的距离是4
m,那么这条抛物线的解析式是( )
A.y=-x2+x+1
B.y=-x2+x-1
C.y=-x2-x+1
D.y=-x2-x-1
二、填空题
9.
某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长50
m),中间用两道墙隔开(如图).已知计划中的建筑材料可建墙的总长度为48
m,则这三间长方形种牛饲养室的总占地面积的最大值为________
m2.
10.
某种商品每件的进价为20元,经调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,则可卖出(30-x)件.若要使销售利润最大,则每件的售价应为________元.
11.
如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900
m(篱笆的厚度忽略不计),当AB=________m时,矩形ABCD的面积最大.
12.
(2020·襄阳)汽车刹车后行驶的距离s(单位:米)关于行驶时间t(单位:秒)的函数关系式是s=15t-6t2,则汽车从刹车到停止所用时间为__________秒.
13.
如图所示是一座抛物线形拱桥,当水面宽为12
m时,桥拱顶部离水面4
m,以水平方向为x轴,建立平面直角坐标系.若选取点A为坐标原点时的抛物线解析式为y=-(x-6)2+4,则选取点B为坐标原点时的抛物线解析式为________________.
14.
某大学生利用业余时间销售一种进价为60元/件的文化衫,前期了解并整理了销售这种文化衫的相关信息如下:
(1)月销量y(件)与售价x(元/件)的关系满足y=-2x+400;
(2)工商部门限制售价x满足70≤x≤150(计算月利润时不考虑其他成本).
给出下列结论:
①这种文化衫的月销量最小为100件;
②这种文化衫的月销量最大为260件;
③销售这种文化衫的月利润最小为2600元;
④销售这种文化衫的月利润最大为9000元.
其中正确的是________.(把所有正确结论的序号都填上)
15.
某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t·
为正整数)的增大而增大,a的取值范围应为________.
16.
竖直上抛的小球离地高度是它运动时间的二次函数.小军相隔1秒依次竖直向上抛出两个小球.假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度.第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t=________.
三、解答题
17.
旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的运营规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入-管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
18.
已知一条双向公路隧道,其横断面由抛物线和矩形ABCD的三边组成,隧道的最大高度为4.9米,AB=10米,BC=2.4米,现把隧道横断面放在如图所示的平面直角坐标系中,有一辆高为4米,宽为2米的装有集装箱的汽车要通过该隧道,如果不考虑其他因素,汽车的右侧至少离开隧道石壁多少米才不至于碰到隧道顶部?
19.
(2019?湘潭)某政府工作报告中强调,2019年着重推进乡村振兴战略,做优做响湘莲等特色农产品品牌.小亮调查了一家湘潭特产店两种湘莲礼盒一个月的销售情况,A种湘莲礼盒进价72元/盒,售价120元/盒,B种湘莲礼盒进价40元/盒,售价80元/盒,这两种湘莲礼盒这个月平均每天的销售总额为2800元,平均每天的总利润为1280元.
(1)求该店平均每天销售这两种湘莲礼盒各多少盒?
(2)小亮调査发现,种湘莲礼盒售价每降3元可多卖1盒.若种湘莲礼盒的售价和销量不变,当种湘莲礼盒降价多少元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是多少元?
20.
如图,排球运动员王亮站在点O处练习发球,将球从点O正上方2
m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与点O的水平距离为9
m,高度为2.43
m,球场的边界距点O的水平距离为18
m.
(1)当h=2.6时,
①求y关于x的函数解析式(不要求写出自变量x的取值范围);
②球能否越过球网?球会不会出界?请说明理由;
③若排球运动员张明站在另外半场的点M(m,0),且张明原地起跳接球的最大高度为2.4
m.若张明因接球的高度不够而失球,求m的取值范围.
(2)若球一定能越过球网,又不出边界,求h的取值范围.
人教版
九年级数学上册
22.3
实际问题与二次函数
同步训练-答案
一、选择题
1.
【答案】B
2.
【答案】B [解析]
由题意知,利润y和月份n之间的函数关系式为y=-n2+12n-11,
∴y=-(n-6)2+25,
当n=1时,y=0;
当n=11时,y=0;
当n=12时,y<0.
故停产的月份是1月、11月和12月.
故选B.
3.
【答案】A [解析]
y=-(x2-4x+4)+4=-(x-2)2+4,∴水喷出的最大高度是4米.
4.
【答案】C [解析]
如图,过点C作CE⊥AB于点E,
则四边形ADCE为矩形,∠DCE=∠CEB=90°,
则∠BCE=∠BCD-∠DCE=30°.
设CD=AE=x
m,则BC=(12-x)m.
在Rt△CBE中,∵∠CEB=90°,∠BCE=30°,
∴BE=BC=(6-x)m,
∴AD=CE==(6
-x)m,AB=AE+BE=x+6-x=(x+6)m,
∴梯形ABCD的面积=(CD+AB)·CE
=(x+x+6)·(6
-x)
=-x2+3
x+18
=-(x-4)2+24
.
∴当x=4时,S最大=24
.
即CD的长为4
m时,梯形储料场ABCD的面积最大为24
m2.故选C.
5.
【答案】D [解析]
①由图象知小球在空中达到的最大高度是40
m,故①错误;
②小球抛出3秒后,速度越来越快,故②正确;
③∵小球抛出3秒时达到最高点,∴速度为0,故③正确;
④设函数解析式为h=a(t-3)2+40,
把O(0,0)代入得0=a(0-3)2+40.
解得a=-,
∴函数解析式为h=-(t-3)2+40.
把h=30代入解析式,得30=-(t-3)2+40,
解得t=4.5或t=1.5,
∴小球的高度h=30
m时,t=1.5
s或4.5
s,故④错误.故选D.
6.
【答案】D [解析]
把y=0代入y=-x2+x+,得-x2+x+=0,
解得x1=10,x2=-2.又∵x>0,∴x=10.
故选D.
7.
【答案】C [解析]
在Rt△ABC中,∠C=90°,AB=10
cm,BC=8
cm,
∴AC==6
cm.
设运动时间为t
s(0
∴S四边形PABQ=S△ABC-S△CPQ=AC·BC-PC·CQ=×6×8-(6-t)×2t=t2-6t+24=(t-3)2+15,
∴当t=3时,四边形PABQ的面积取得最小值,最小值为15
cm2.
故选C.
8.
【答案】A [解析]
A,B两点的坐标分别为(4,0),(0,1),把(4,0),(0,1)分别代入y=-x2+bx+c,求出b,c的值即可.
二、填空题
9.
【答案】144 【解析】∵围墙的总长为50
m,设3间饲养室合计长x
m,则饲养室的宽=
m,∴总占地面积为y=x·=-x2+12x(0<x<48),由y=-x2+12x=-(x-24)2+144,∵x=24在0<x<48范围内,a=-<0,∴在0<x≤24范围内,y随x的增大而增大,∴x=24时,y取得最大值,y最大=144
m2.
10.
【答案】25 [解析]
设利润为w元,则w=(x-20)(30-x)=-(x-25)2+25.
∵20≤x≤30,
∴当x=25时,二次函数有最大值25.
11.
【答案】150 [解析]
设AB=x
m,则AB=EF=CD=x
m,所以AD=BC=(900-3x)m.设矩形ABCD的面积为y
m2,则y=x·(900-3x)=-x2+450x(0<x<300).由于二次项系数小于0,所以y有最大值,且当x=-=-=150时,函数y取得最大值.
故当AB=150
m矩形ABCD的面积最大.
12.
【答案】2.5.
【解析】令s=0,得15t-6t2=0,解得t1=2.5,t2=0(不合题意,舍去),故答案为2.5.
13.
【答案】y=-(x+6)2+4
14.
【答案】①②③ [解析]
由题意知,当70≤x≤150时,y=-2x+400,
∵-2<0,∴y随x的增大而减小,
∴当x=150时,y取得最小值,最小值为100,故①正确;
当x=70时,y取得最大值,最大值为260,故②正确;
设销售这种文化衫的月利润为W元,
则W=(x-60)(-2x+400)=-2(x-130)2+9800,
∵70≤x≤150,
∴当x=70时,W取得最小值,最小值为-2(70-130)2+9800=2600,故③正确;
当x=130时,W取得最大值,最大值为9800,故④错误.
故答案为①②③.
15.
【答案】0
【答案】1.6
秒 【解析】本题主要考查了二次函数的对称性问题.由题意可知,各自抛出后1.1秒时到达相同最大离地高度,即到达二次函数图象的顶点处,故此二次函数图象的对称轴为t=1.1;由于两次抛小球的时间间隔为1秒,所以当第一个小球和第二个小球到达相同高度时,则这两个小球必分居对称轴左右两侧,由于高度相同,则在该时间节点上,两小球对应时间到对称轴距离相同.
故该距离为0.5秒,
所以此时第一个小球抛出后t=1.1+0.5=1.6秒时与第二个小球的离地高度相同.
三、解答题
17.
【答案】
解:(1)由题意知,若观光车能全部租出,则0
解得x>22,(3分)
又∵x是5的倍数,
∴每辆车的日租金至少应为25元.(5分)
(2)设每天的净收入为y元,
当0
∴当x=100时,y1的最大值为50×100-1100=3900;(8分)
当x>100时,y2=(50-)x-1100=-x2+70x-1100=-(x-175)2+5025.(9分)
∴当x=175时,y2的最大值是5025,
∵5025>3900,
∴当每辆车的日租金为175元时,每天的净收入最多是5025元.(10分)
18.
【答案】
解:由题意,知AB=10米,BC=2.4米,
∴C(10,0),B(10,-2.4),A(0,-2.4).
由题意,知抛物线的顶点坐标为(5,2.5).
设抛物线的解析式为y=a(x-5)2+2.5.
将(10,0)代入解析式,
得0=a(10-5)2+2.5,
解得a=-,
∴y=-(x-5)2+2.5=-x2+x.
此公路为双向公路,当汽车高为4米时,在抛物线隧道中对应的纵坐标y=4-2.4=1.6,
由1.6=-x2+x,
解得x1=2,x2=8.
故汽车要通过隧道,其右侧至少要离开隧道石壁2米才不至于碰到隧道顶部.
19.
【答案】
(1)根据题意,可设平均每天销售礼盒盒,种礼盒为盒,
则有,解得,
故该店平均每天销售礼盒10盒,种礼盒为20盒.
(2)设A种湘莲礼盒降价元/盒,利润为元,依题意
总利润,
化简得,
∵,
∴当时,取得最大值为1307,
故当种湘莲礼盒降价9元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是1307元.
20.
【答案】
解:(1)①把x=0,y=2及h=2.6代入y=a(x-6)2+h,得2=a(0-6)2+2.6,
∴a=-,
∴y=-(x-6)2+2.6.
②球能越过球网,球会出界.理由如下:
由①知y=-(x-6)2+2.6,
当x=9时,y=-×(9-6)2+2.6=2.45>2.43,
∴球能越过球网.
当x=18时,y=-×(18-6)2+2.6=0.2>0,∴球会出界.
③若运动员张明原地起跳到最大高度时刚好接到球,此时-(m-6)2+2.6=2.4,
解得m1=6+2
,m2=6-2
.
∵张明接球高度不够,∴6-2
<m<6+2
.∵张明在另外半场,
∴m的取值范围为9<m<6+2
.
(2)将x=0,y=2代入y=a(x-6)2+h,得a=.
当x=9时,y=(9-6)2+h=>2.43;①
当x=18时,y=(18-6)2+h=8-3h≤0.②
由①②,得h≥.
同课章节目录
