苏科版七年级数学上册6.3 余角、补角、对顶角_(2) 课件(12张PPT)
文档属性
| 名称 | 苏科版七年级数学上册6.3 余角、补角、对顶角_(2) 课件(12张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 556.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 00:00:00 | ||
图片预览




文档简介
(共12张PPT)
余角、补角、对顶角
观察与思考
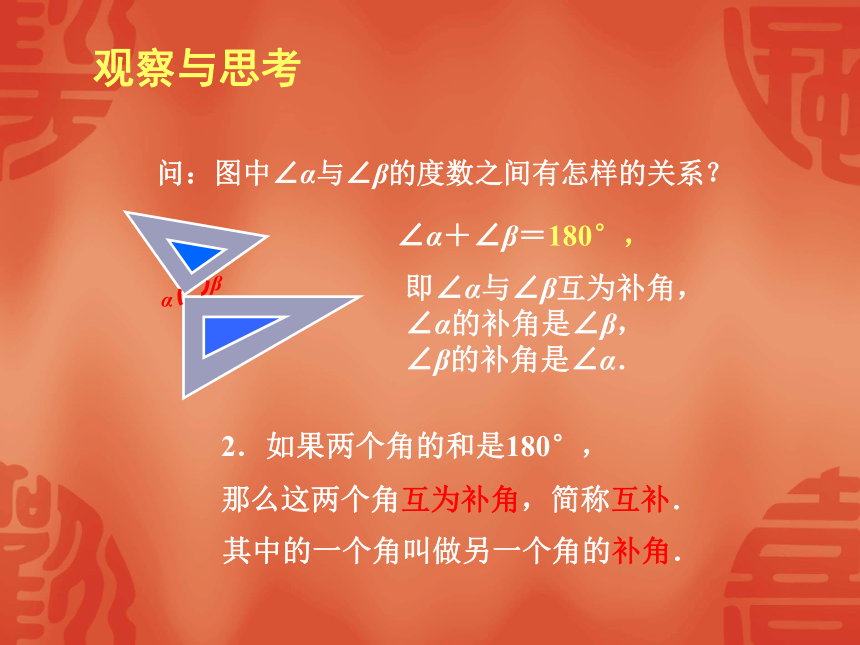
问:图中∠α与∠β的度数之间有怎样的关系?
α
β
1.如果两个角的和是90°,
那么这两个角互为余角,简称互余.
其中的一个角叫做另一个角的余角.
即∠α与∠β互为余角,
∠α的余角是∠β,
∠β的余角是∠α.
∠α+∠β=90°,
问:图中∠α与∠β的度数之间有怎样的关系?
观察与思考
α
β
2.如果两个角的和是180°,
那么这两个角互为补角,简称互补.
其中的一个角叫做另一个角的补角.
即∠α与∠β互为补角,
∠α的补角是∠β,
∠β的补角是∠α.
∠α+∠β=180°,
做一做
∠α的度数
∠α的余角
∠α的补角
(0<n<90)
想一想:同一个角的补角与它的余角之间有怎样的数量关系?
40°
130°
45°
135°
60°
30°
(90-n)
°
(180-n)
°
同一个角的补角与它的余角相差900.
做一做
A组
B组
C组
(1)对A组中的每一个角,在B组中找出它的补角,并用线连接;
(2)B组中有哪些角的余角在C组中?分别找出这些角,并用线连接.
思考:怎样的角有余角、怎样的角有补角?
练一练
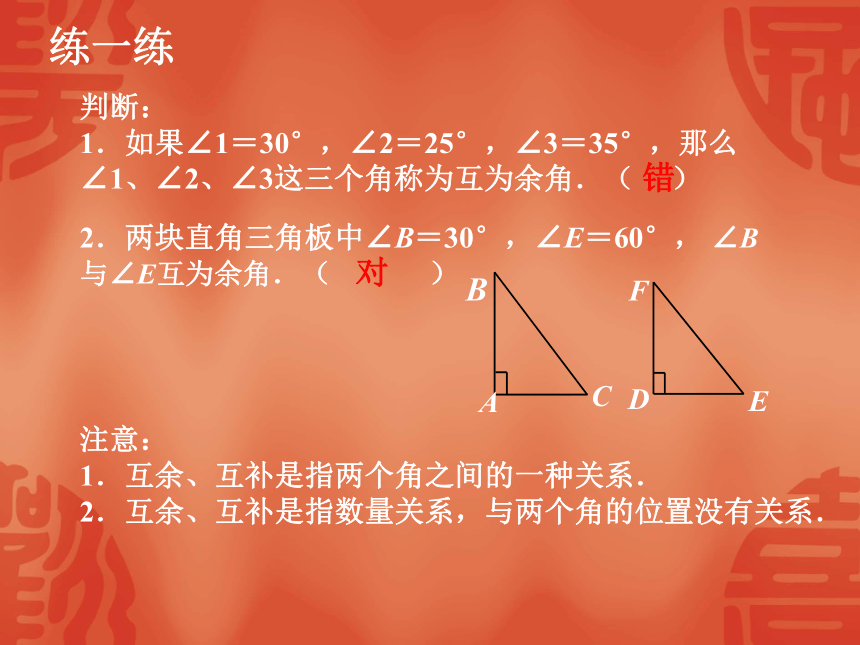
判断:
1.如果∠1=30°,∠2=25°,∠3=35°,那么∠1、∠2、∠3这三个角称为互为余角.(
)
错
2.两块直角三角板中∠B=30°,∠E=60°,
∠B与∠E互为余角.(
)
对
B
A
C
F
D
E
注意:
1.互余、互补是指两个角之间的一种关系.
2.互余、互补是指数量关系,与两个角的位置没有关系.
例1
如图,如果∠1与∠
2互为余角,
∠1与∠3互为余角,那么∠2与∠3相等吗?为什么?
解:
∠2与∠3相等.
因为∠1与∠
2互为余角,
∠1与∠3互为余角,
所以
∠
2=
90
°-∠1,
∠3=
90
°-∠1,
所以∠2=∠3.
同角(或等角)的余角相等;
如图,如果∠α与∠β互为补角,∠
α与∠γ互为补角,那么∠
β与∠
γ相等吗?为什么?
解:
∠β与∠γ相等.
因为∠α与∠
β互为补角,
∠α与∠γ互补,
所以
∠β=
180
°-∠α
,∠γ=
180
°-∠α
所以∠β
=∠γ.
同角(或等角)的补角相等.
思考:
练一练
1.如图1,∠AOC=900,∠BOD=900,则∠1与∠3的关系是_____,其理由是__________________________.
相等
同角的余角相等
2.如图2,∠1+∠2=1800,∠3+∠4=1800,
若∠1=∠3,则∠2与∠4的关系是_______,
其理由是_________________.
相等
等角的补角相等
1
2
3
A
B
C
D
O
图1
1
2
3
4
图2
已知∠α与∠β互为补角,且∠β比∠α大30°,求∠α、∠β的度数
.
解:根据题意,可得∠β=∠α+30°,
因为∠α与∠β互为补角,所以∠α+∠β=180°,
即∠α+(∠α+30°)=180°,
所以∠α=75°,∠β=75°+30°=105°.
互为余角
互为补角
图形
数量关系
性
质
1
2
∠1+∠2=90°
同角(或等角)的余角相等
1
2
∠1+∠2=180°
同角(或等角)的补角相等
知识总结:
能力总结:
1.学习了余角、补角、对顶角的概念及其性质;
2.经历“观察——猜想——说理”的认知过程,发展了对图形的观察能力和有条理的表达能力.
3.体会到数学知识在日常生活中的作用.
余角、补角、对顶角
观察与思考
问:图中∠α与∠β的度数之间有怎样的关系?
α
β
1.如果两个角的和是90°,
那么这两个角互为余角,简称互余.
其中的一个角叫做另一个角的余角.
即∠α与∠β互为余角,
∠α的余角是∠β,
∠β的余角是∠α.
∠α+∠β=90°,
问:图中∠α与∠β的度数之间有怎样的关系?
观察与思考
α
β
2.如果两个角的和是180°,
那么这两个角互为补角,简称互补.
其中的一个角叫做另一个角的补角.
即∠α与∠β互为补角,
∠α的补角是∠β,
∠β的补角是∠α.
∠α+∠β=180°,
做一做
∠α的度数
∠α的余角
∠α的补角
(0<n<90)
想一想:同一个角的补角与它的余角之间有怎样的数量关系?
40°
130°
45°
135°
60°
30°
(90-n)
°
(180-n)
°
同一个角的补角与它的余角相差900.
做一做
A组
B组
C组
(1)对A组中的每一个角,在B组中找出它的补角,并用线连接;
(2)B组中有哪些角的余角在C组中?分别找出这些角,并用线连接.
思考:怎样的角有余角、怎样的角有补角?
练一练
判断:
1.如果∠1=30°,∠2=25°,∠3=35°,那么∠1、∠2、∠3这三个角称为互为余角.(
)
错
2.两块直角三角板中∠B=30°,∠E=60°,
∠B与∠E互为余角.(
)
对
B
A
C
F
D
E
注意:
1.互余、互补是指两个角之间的一种关系.
2.互余、互补是指数量关系,与两个角的位置没有关系.
例1
如图,如果∠1与∠
2互为余角,
∠1与∠3互为余角,那么∠2与∠3相等吗?为什么?
解:
∠2与∠3相等.
因为∠1与∠
2互为余角,
∠1与∠3互为余角,
所以
∠
2=
90
°-∠1,
∠3=
90
°-∠1,
所以∠2=∠3.
同角(或等角)的余角相等;
如图,如果∠α与∠β互为补角,∠
α与∠γ互为补角,那么∠
β与∠
γ相等吗?为什么?
解:
∠β与∠γ相等.
因为∠α与∠
β互为补角,
∠α与∠γ互补,
所以
∠β=
180
°-∠α
,∠γ=
180
°-∠α
所以∠β
=∠γ.
同角(或等角)的补角相等.
思考:
练一练
1.如图1,∠AOC=900,∠BOD=900,则∠1与∠3的关系是_____,其理由是__________________________.
相等
同角的余角相等
2.如图2,∠1+∠2=1800,∠3+∠4=1800,
若∠1=∠3,则∠2与∠4的关系是_______,
其理由是_________________.
相等
等角的补角相等
1
2
3
A
B
C
D
O
图1
1
2
3
4
图2
已知∠α与∠β互为补角,且∠β比∠α大30°,求∠α、∠β的度数
.
解:根据题意,可得∠β=∠α+30°,
因为∠α与∠β互为补角,所以∠α+∠β=180°,
即∠α+(∠α+30°)=180°,
所以∠α=75°,∠β=75°+30°=105°.
互为余角
互为补角
图形
数量关系
性
质
1
2
∠1+∠2=90°
同角(或等角)的余角相等
1
2
∠1+∠2=180°
同角(或等角)的补角相等
知识总结:
能力总结:
1.学习了余角、补角、对顶角的概念及其性质;
2.经历“观察——猜想——说理”的认知过程,发展了对图形的观察能力和有条理的表达能力.
3.体会到数学知识在日常生活中的作用.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
