苏科版七年级数学上册第2章 有理数 复习 课件(33张PPT)
文档属性
| 名称 | 苏科版七年级数学上册第2章 有理数 复习 课件(33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 844.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 00:00:00 | ||
图片预览









文档简介
(共33张PPT)
第2章
有理数
复习课件
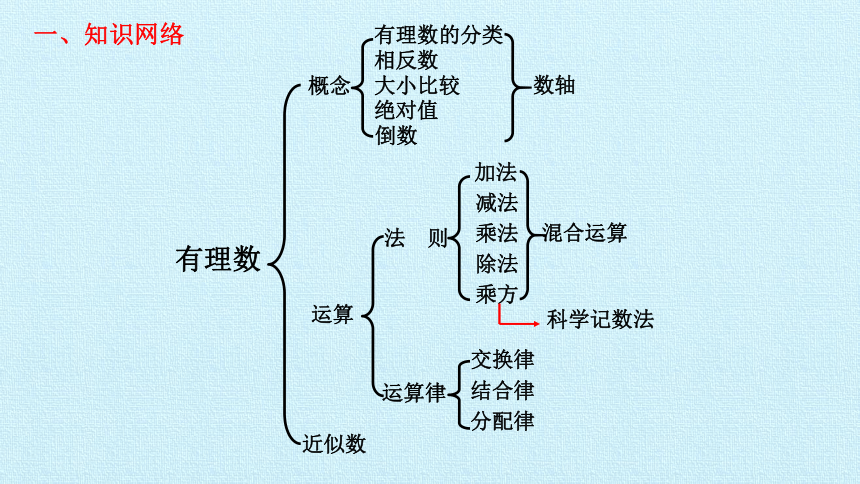
一、知识网络
有理数
概念
运算
有理数的分类
相反数
大小比较
法
则
运算律
数轴
近似数
绝对值
倒数
加法
减法
乘法
除法
乘方
混合运算
交换律
科学记数法
结合律
分配律
1.正数、负数
2.有理数
3.数轴
4.相反数
5.倒数
6.有理数的绝对值
7.有理数大小的比较
8.科学记数法、近似数
一、有理数的基本概念
有理数总复习
二、有理数的运算
加、减、乘、除、乘方运算
一、有理数的基本概念
负数:
在正数前面加“—”的数;
0既不是正数,也不是负数。
1.正数:大于零的数叫正数
在同一问题中,正数与负数分别表示相反意义的数量。
1.水位上升0.5米记为+0.5米,
水位下降1.5米记为_______,
水位不升不降记为______,
水位上升-2米表示__________。
2.-a一定是负数吗?
3.一袋面粉的质量标记为“25±0.25”,则下列面粉中合格的有(
)
A.24.70千克
B.25.30千克
C.25.51千克
D.24.80千克
-1.5
0
下降2米
D
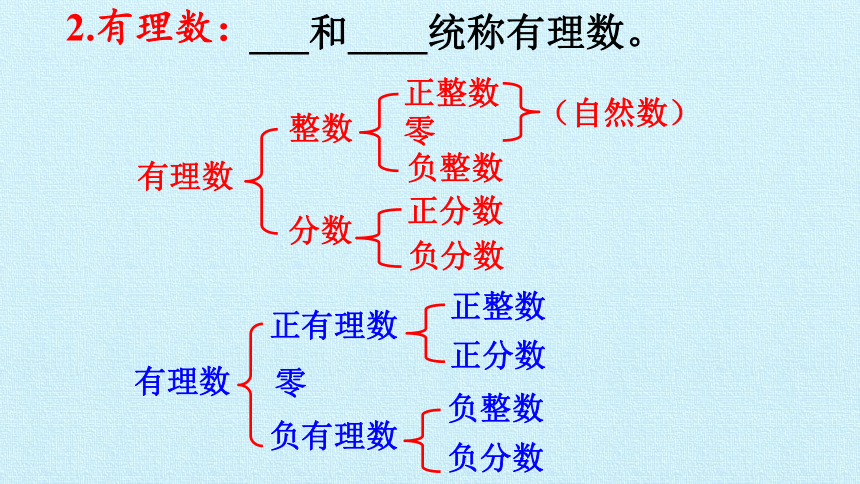
2.有理数:
___和____统称有理数。
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
(自然数)
把下列各数填在相应的集合中:
正数集合:{
…}
负数集合:{
…}
整数集合:{
…}
负分数集合:{
…}
有理数集合:{
…}
27,-14,0
1.判断下列说法是否正确。
一个有理数不是整数就是分数;
(
)
一个有理数不是正数就是负数;
(
)
一个整数不是正的就是负的;
(
)
一个分数不是正的就是负的
(
)
?
?
?
?
2.最大的正整数
最小的正整数
最大的负整数
最小的负整数
最小的自然数
最小的非负数
最大的有理数、最小的有理数、最大的整数、最小的整数都不存在。
不存在
1
-1
不存在
0
0
3.下列说法错误的是(
)
(A)自然数一定是有理数(B)自然数一定是整数
(C)自然数一定是非负数(D)整数一定是自然数
D
3.数轴:
规定了原点、正方向和单位长度的直线
1)在数轴上表示的两个数,右边的数总比左边的数大;
2)正数都大于0,负数都小于0;正数大于一切负数;
-3
–2
–1
0
1
2
3
4
3)所有有理数都可以用数轴上的点表示。
数轴上的点与其所表示的数一一对应。
4)数轴上两点之间的距离等于这两点所表示的两数的差的绝对值。
1.在数轴上,原点及原点左边所表示的数是( )
A整数 B负数 C非负数 D非正数
2.下列语句中正确的是( )
A数轴上的点只能表示整数
B数轴上的点只能表示分数
C数轴上的点只能表示有理数
D所有有理数都可以用数轴上的点表示出来
D
D
3.+3表示的点与-2表示的点距离是____个单位。
5
4.与原点的距离为3个单位的点有__个,是________
2
-3和+3
5.与+3表示的点距离2000个单位的点有___个,
他们分别表示的有理数是______和______。
2
2003
-1997
6.数轴上A距原点2个单位长度,A向左移动3个单位长度,再向右移动1个单位长度后,A表示_________。
0或-4
7.数轴上将B向右移动3个单位长度,再向左移动5个单位长度,终点表示0,那么B表示________。
2
8.已知有理数a、b、c在数轴上的位置如图,化简:
|a|-|a+b|+|c-a|+|b+c|
b
a
0
c
-a
-48或80
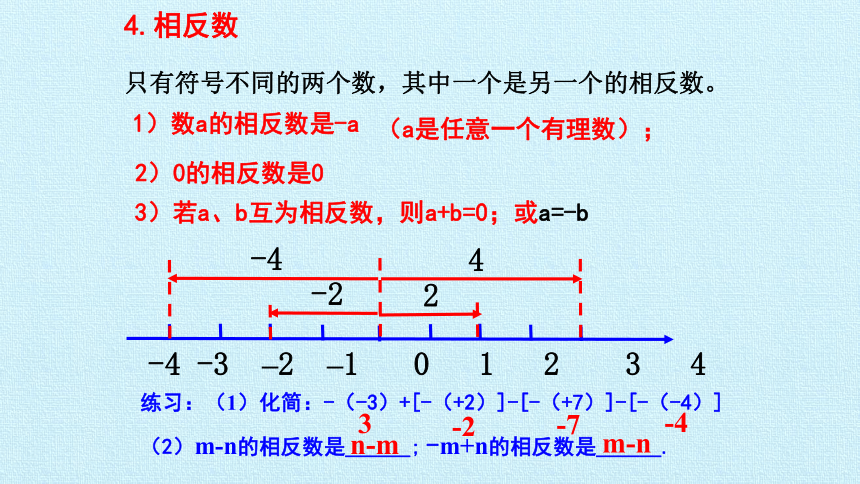
4.相反数
只有符号不同的两个数,其中一个是另一个的相反数。
1)数a的相反数是-a
2)0的相反数是0
-4
-3
–2
–1
0
1
2
3
4
-2
2
-4
4
3)若a、b互为相反数,则a+b=0;或a=-b
(a是任意一个有理数);
练习:(1)化简:-(-3)+[-(+2)]-[-(+7)]-[-(-4)]
(2)m-n的相反数是______;
-m+n的相反数是______.
3
-2
-7
-4
n-m
m-n
乘积是1的两个数互为倒数。
1)a的倒数是
(a≠0);
3)若a与b互为倒数,则ab=1
2)0没有倒数;
5.倒数
1.下列各数,哪两个数互为倒数?
8,
,-1,+(-8),1,
2.a、b互为相反数且都不为0,则
的值(
)A、-1 B、0 C、1 D、2
3.如果两个有理数的和除以它们的积,所得的商是零,那么这两个有理数(
)A.互为相反数,但不等于零
B.互为倒数
C.有一个等于零
D.都等于零
4.下列各式中,是互为倒数的是(
)
A、a-b和b-a
B、(-1)×(-1)和-(1÷1)
C、1÷m和m÷1
D、2÷6和
B
A
C
6.绝对值
当a≥0时,|a|=a
当a≤0时,|a|=-a
不要忽略=“0”
几何意义:|a|----在数轴上表示数a的点到原点的距离
|a-b|-----在数轴上表示数a的点到表示数b的点的距离
性质|a|≥0
1)绝对值小于2的整数有________。
2)绝对值等于它本身的数有___________。
3)绝对值不大于3的负整数有__________。
4)数a和b的绝对值分别为2和5,且在数轴上表示a的点在表示b的点左侧,则b的值为
。
0,±1
零和正数
-1,-2,-3
5
练习:
(1)任何数的绝对值都是_____数
(2)若a=b,则|a|___|b|
(3)若a+b=0,则|a|___|b|
(4)若|a|=|b|,则a、b的关系是_________
(5)若|a|+a=0,则a_____
(6)若|-a|=a,则a_____
(7)若|x|=2,则x=_____
(8)绝对值大于3而不大于6的整数有______
(9)|x-2|=1,则x=_______
(10)
非负
=
±2
≥0
≤0
相等或者互为相反数
=
1或3
-1或3
±4,±5,±6
1、若(x-1)2+|y+4|=0,则3x+5y=______
2、若|a-3|+|3a-4b|=0,则-2a+8b=____
3、若|3-?|+|4-?|=_______
12
非负数性质的应用
两个非负数之和为零,则这两个非负数都是零
4、如果
,求
的值。
5、对于任何有理数a,下列各式中一定为负数的是(
)
(A)-(-3+a)
(B)-a
(C)-|a+1|(D)-a2-1
6、已知|x|=3,|y|=2,且x-1或-5
-17
1
9
D
0
5
7、当a=
时,5-a2有最大值为
。
7.利用绝对值比较有理数的大小
两个负数比较大小,绝对值大的数小
即若a<0,b<0,且|a|>|b|,则a<
<
<
B
8.科学记数法和近似数
把一个绝对值大于10的数N写成a×10n的形式,其中,1≤|a|<10,n等于N的整数位数减1
3.02×105
1)下列各数用科学计数法表示:
163010000
13亿
-35048.2
2)4.2×104
有_______个整数位
3)下列各数各精确到哪一位?
0.045
12500
2.06万
4)0.34628精确到百分位_________
5)862700精确到千位________
精确到万位是________
6)1.45×105
1.6301×108
1.3×109
-3.50482×104
5
千分位
个位
百位
千位
0.35
8.63×105
1.5×105
二、有理数的运算律
1)加法交换律
a+b=b+a
2)加法结合律
(a+b)+c=a+(b+c)
3)乘法交换律
ab=ba
4)乘法结合律
(ab)c=a(bc)
5)分配律
a(b+c)=ab+ac
有理数运算
有理数的加法
a>0,b>0,则a+b>0且|a+b|=|a|+|b|
即a+b=|a|+|b|
a<0,b<0,则a+b<0且|a+b|=|a|+|b|
即a+b=-(|a|+|b|)
a>0,b<0,|a|>|b|,则a+b>0且|a+b|=|a|-|b|
即a+b=|a|-|b|
a>0,b<0,|a|<|b|,则a+b<0且|a+b|=|b|-|a|
即a+b=-(|b|-|a|)
有理数的减法进制a-b=a+(-b)
大数减小数,差为正;
小数减大数,差为负。
注意带有绝对值符号的题目的简算
加减法可以统一成加法
1.把下式写成省略加号的和的形式,并把它读出来
(-3)+(-8)-(-6)+(-7)
解:原式=(-3)+(-8)+(+6)+(-7)
=-3-8+6-7
读作:-3,-8,+6,-7的和或负3减8加6减7
加法四结合
1.凑整结合法
2.同号结合法
3.两个相反数结合法
4.同分母或易通分的分数结合法
解
题
技
能
1或-6
1.5.6+(-0.9)+4.4+(-8.1)+(-1)
3.(+7)-(-15)+(-12)-(+7)
4.1-4+7-10+13-16+19-22
6.1+2-3-4+5+6-7-8+……+2001+2002-2003-2004
7.|2x+5|=7,则x=________
0
-4
3
-12
0
-2004
有理数的乘除法
0×a=0
若a>0,b>0,则ab>0;若a<0,b<0,则ab>0
若a>0,b<0,则ab<0;若a<0,b>0,则ab<0
(b≠0)
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,都得0
①几个不等于0的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正
②几个数相乘,有一个因数为0,积就为0
两数相除,同号得正,异号得负,并把绝对值相除;
0除以任何一个不等于0的数,都得0
除以一个不为零的数等于乘以
这个数的倒数
例1、计算:
(1)-150+250;
(2)-15+(-23);
(3)-5-65;
(4)-26-(-15);
(5)-6×(-16);
(6)
;
(7)8÷(-16);
(8)
;
100
-38
-70
-11
96
-9
-1/2
75/2
例2、判断下列计算是否正确,如果不正确,请改正。
(1)-22=(-2)2=-(-22)
(2)
(3)-13-3=-10
(4)-17+3=-20
×
×
×
×
-13-3=-16
(-2)2=-(-22)
-17+3=-14
(5)6÷(2+3)=6÷2+6÷3
(6)(2+3)÷6=2÷6+3÷6
(7)
(8)
×
√
×
×
6÷(2+3)=1.2
例4、计算:(1)(-0.02)×(-20)×(-5)×4.5;
(2)
(3)
(4)
例3、计算:(1)-2-|-3|;
(2)|-2-(-3)|
(5)-66×4-(-2.5)÷(-0.1);
(6)
;
(7)(-2)2×5-(-2)3÷4;
(8)-(3-5)+32×(1-3)
-5
1
-9
39/5
5.3
3
-289
-258
22
-16
解题技能
乘法三结合
1、积为整数结合
2、两个倒数结合
3、能约分的结合
-7
-10/7
-4
分配律
分配律反着用
分配律计算技巧
真假分配律
×
√
-29
3
4.58
-1
256
-179.25
有理数的乘方
①求n个相同因数的积的运算,叫做乘方
②正数的任何次幂都是_____;
负数的奇次幂是_____,
负数的偶次幂是_____
幂
指数
底数
a·a·a····
·a
n个
=
正数
负数
正数
1.(-1)2n
=
(-1)2n+1
=
-1n
=
(-1)n
=
(-a)2n
=
(-a)2n+1=
若a>0,则-a
n
____0;若a>0,则(-a)n
的符号是什么?(1)a2___0
(-a)3=______
(-a)4=_____
(2)a2=4,则a=_____;
(-a)2=4,则a=_____
±2
±2
≥
-a3
a4
1
-1
-1
当n为奇数时-1当n为偶数时1
<
2.平方是它本身的数有__________
3.立方是它本身的数有__________
4.某种细胞每过30分钟便由1个分裂成2个。经过5小时后一个细胞可以分裂成_____个细胞。
5.比较大小
0,1
0,1,-1
1024
6.2×32和(2×3)2有什么区别?各等于什么?
7.32和23有什么区别?各等于什么?
8.-34和(-3)4有什么区别?各等于什么?
9.
10.若0<a<1,则
之间的大小关系为(
)
A.
B.
C.
D.不能确定大小
有理数的混合运算顺序:先乘方,再乘除,最后加减。有括号,先算括号里面的;同级运算,应从左往右运。
做题时注意先观察题目整体特点,能简算的简算。
达标计算:
(3)
(4)
(5)
1.某一出租车一天下午以鼓楼为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下:+9、3、5、+4、8、+6、3、6、4、+10
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
2.已知:
互为相反数
求:
的值
达标试题:
星期
一
二
三
四
五
六
每股涨跌
+4
+4.5
-1
-2.5
-6
+2
3.小红爸爸上星期六买进某公司股票1000股,每股27元,上表为本周内每日该股票的涨跌情况。(单位:元)
(1)通过上表你认为星期三收盘时,每股是多少?
(2)本周内每股最高是多少?最低是多少元?
(3)已知小红爸爸买进股票时付了1.5‰的手续费,卖出时还需付成交额1.5‰的手续费和1‰的交易税,如果小红爸爸在星期六收盘时将全部股票卖出,你对他的收益情况怎样评价?
解:(1)27+4+4.5+(-1)=34.5
(2)27+4+4.5=35.5;27+4+4.5+(-1)+(-2.5)+(-6)+2=28.
(3)28×1000-[28×1000×﹙1.5‰+1‰﹚+27×1000×﹙1+1.5‰﹚]=28000-[70+27000+40.5]=28000-27110.5=889.5
答:(1)每股是34.5元
(2)每股最高是35.5元,最低是28元。
(3)星期六收盘时将全部股票卖出,盈利889.5元。
谢
谢
第2章
有理数
复习课件
一、知识网络
有理数
概念
运算
有理数的分类
相反数
大小比较
法
则
运算律
数轴
近似数
绝对值
倒数
加法
减法
乘法
除法
乘方
混合运算
交换律
科学记数法
结合律
分配律
1.正数、负数
2.有理数
3.数轴
4.相反数
5.倒数
6.有理数的绝对值
7.有理数大小的比较
8.科学记数法、近似数
一、有理数的基本概念
有理数总复习
二、有理数的运算
加、减、乘、除、乘方运算
一、有理数的基本概念
负数:
在正数前面加“—”的数;
0既不是正数,也不是负数。
1.正数:大于零的数叫正数
在同一问题中,正数与负数分别表示相反意义的数量。
1.水位上升0.5米记为+0.5米,
水位下降1.5米记为_______,
水位不升不降记为______,
水位上升-2米表示__________。
2.-a一定是负数吗?
3.一袋面粉的质量标记为“25±0.25”,则下列面粉中合格的有(
)
A.24.70千克
B.25.30千克
C.25.51千克
D.24.80千克
-1.5
0
下降2米
D
2.有理数:
___和____统称有理数。
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
(自然数)
把下列各数填在相应的集合中:
正数集合:{
…}
负数集合:{
…}
整数集合:{
…}
负分数集合:{
…}
有理数集合:{
…}
27,-14,0
1.判断下列说法是否正确。
一个有理数不是整数就是分数;
(
)
一个有理数不是正数就是负数;
(
)
一个整数不是正的就是负的;
(
)
一个分数不是正的就是负的
(
)
?
?
?
?
2.最大的正整数
最小的正整数
最大的负整数
最小的负整数
最小的自然数
最小的非负数
最大的有理数、最小的有理数、最大的整数、最小的整数都不存在。
不存在
1
-1
不存在
0
0
3.下列说法错误的是(
)
(A)自然数一定是有理数(B)自然数一定是整数
(C)自然数一定是非负数(D)整数一定是自然数
D
3.数轴:
规定了原点、正方向和单位长度的直线
1)在数轴上表示的两个数,右边的数总比左边的数大;
2)正数都大于0,负数都小于0;正数大于一切负数;
-3
–2
–1
0
1
2
3
4
3)所有有理数都可以用数轴上的点表示。
数轴上的点与其所表示的数一一对应。
4)数轴上两点之间的距离等于这两点所表示的两数的差的绝对值。
1.在数轴上,原点及原点左边所表示的数是( )
A整数 B负数 C非负数 D非正数
2.下列语句中正确的是( )
A数轴上的点只能表示整数
B数轴上的点只能表示分数
C数轴上的点只能表示有理数
D所有有理数都可以用数轴上的点表示出来
D
D
3.+3表示的点与-2表示的点距离是____个单位。
5
4.与原点的距离为3个单位的点有__个,是________
2
-3和+3
5.与+3表示的点距离2000个单位的点有___个,
他们分别表示的有理数是______和______。
2
2003
-1997
6.数轴上A距原点2个单位长度,A向左移动3个单位长度,再向右移动1个单位长度后,A表示_________。
0或-4
7.数轴上将B向右移动3个单位长度,再向左移动5个单位长度,终点表示0,那么B表示________。
2
8.已知有理数a、b、c在数轴上的位置如图,化简:
|a|-|a+b|+|c-a|+|b+c|
b
a
0
c
-a
-48或80
4.相反数
只有符号不同的两个数,其中一个是另一个的相反数。
1)数a的相反数是-a
2)0的相反数是0
-4
-3
–2
–1
0
1
2
3
4
-2
2
-4
4
3)若a、b互为相反数,则a+b=0;或a=-b
(a是任意一个有理数);
练习:(1)化简:-(-3)+[-(+2)]-[-(+7)]-[-(-4)]
(2)m-n的相反数是______;
-m+n的相反数是______.
3
-2
-7
-4
n-m
m-n
乘积是1的两个数互为倒数。
1)a的倒数是
(a≠0);
3)若a与b互为倒数,则ab=1
2)0没有倒数;
5.倒数
1.下列各数,哪两个数互为倒数?
8,
,-1,+(-8),1,
2.a、b互为相反数且都不为0,则
的值(
)A、-1 B、0 C、1 D、2
3.如果两个有理数的和除以它们的积,所得的商是零,那么这两个有理数(
)A.互为相反数,但不等于零
B.互为倒数
C.有一个等于零
D.都等于零
4.下列各式中,是互为倒数的是(
)
A、a-b和b-a
B、(-1)×(-1)和-(1÷1)
C、1÷m和m÷1
D、2÷6和
B
A
C
6.绝对值
当a≥0时,|a|=a
当a≤0时,|a|=-a
不要忽略=“0”
几何意义:|a|----在数轴上表示数a的点到原点的距离
|a-b|-----在数轴上表示数a的点到表示数b的点的距离
性质|a|≥0
1)绝对值小于2的整数有________。
2)绝对值等于它本身的数有___________。
3)绝对值不大于3的负整数有__________。
4)数a和b的绝对值分别为2和5,且在数轴上表示a的点在表示b的点左侧,则b的值为
。
0,±1
零和正数
-1,-2,-3
5
练习:
(1)任何数的绝对值都是_____数
(2)若a=b,则|a|___|b|
(3)若a+b=0,则|a|___|b|
(4)若|a|=|b|,则a、b的关系是_________
(5)若|a|+a=0,则a_____
(6)若|-a|=a,则a_____
(7)若|x|=2,则x=_____
(8)绝对值大于3而不大于6的整数有______
(9)|x-2|=1,则x=_______
(10)
非负
=
±2
≥0
≤0
相等或者互为相反数
=
1或3
-1或3
±4,±5,±6
1、若(x-1)2+|y+4|=0,则3x+5y=______
2、若|a-3|+|3a-4b|=0,则-2a+8b=____
3、若|3-?|+|4-?|=_______
12
非负数性质的应用
两个非负数之和为零,则这两个非负数都是零
4、如果
,求
的值。
5、对于任何有理数a,下列各式中一定为负数的是(
)
(A)-(-3+a)
(B)-a
(C)-|a+1|(D)-a2-1
6、已知|x|=3,|y|=2,且x
-17
1
9
D
0
5
7、当a=
时,5-a2有最大值为
。
7.利用绝对值比较有理数的大小
两个负数比较大小,绝对值大的数小
即若a<0,b<0,且|a|>|b|,则a
<
<
B
8.科学记数法和近似数
把一个绝对值大于10的数N写成a×10n的形式,其中,1≤|a|<10,n等于N的整数位数减1
3.02×105
1)下列各数用科学计数法表示:
163010000
13亿
-35048.2
2)4.2×104
有_______个整数位
3)下列各数各精确到哪一位?
0.045
12500
2.06万
4)0.34628精确到百分位_________
5)862700精确到千位________
精确到万位是________
6)1.45×105
1.6301×108
1.3×109
-3.50482×104
5
千分位
个位
百位
千位
0.35
8.63×105
1.5×105
二、有理数的运算律
1)加法交换律
a+b=b+a
2)加法结合律
(a+b)+c=a+(b+c)
3)乘法交换律
ab=ba
4)乘法结合律
(ab)c=a(bc)
5)分配律
a(b+c)=ab+ac
有理数运算
有理数的加法
a>0,b>0,则a+b>0且|a+b|=|a|+|b|
即a+b=|a|+|b|
a<0,b<0,则a+b<0且|a+b|=|a|+|b|
即a+b=-(|a|+|b|)
a>0,b<0,|a|>|b|,则a+b>0且|a+b|=|a|-|b|
即a+b=|a|-|b|
a>0,b<0,|a|<|b|,则a+b<0且|a+b|=|b|-|a|
即a+b=-(|b|-|a|)
有理数的减法进制a-b=a+(-b)
大数减小数,差为正;
小数减大数,差为负。
注意带有绝对值符号的题目的简算
加减法可以统一成加法
1.把下式写成省略加号的和的形式,并把它读出来
(-3)+(-8)-(-6)+(-7)
解:原式=(-3)+(-8)+(+6)+(-7)
=-3-8+6-7
读作:-3,-8,+6,-7的和或负3减8加6减7
加法四结合
1.凑整结合法
2.同号结合法
3.两个相反数结合法
4.同分母或易通分的分数结合法
解
题
技
能
1或-6
1.5.6+(-0.9)+4.4+(-8.1)+(-1)
3.(+7)-(-15)+(-12)-(+7)
4.1-4+7-10+13-16+19-22
6.1+2-3-4+5+6-7-8+……+2001+2002-2003-2004
7.|2x+5|=7,则x=________
0
-4
3
-12
0
-2004
有理数的乘除法
0×a=0
若a>0,b>0,则ab>0;若a<0,b<0,则ab>0
若a>0,b<0,则ab<0;若a<0,b>0,则ab<0
(b≠0)
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,都得0
①几个不等于0的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正
②几个数相乘,有一个因数为0,积就为0
两数相除,同号得正,异号得负,并把绝对值相除;
0除以任何一个不等于0的数,都得0
除以一个不为零的数等于乘以
这个数的倒数
例1、计算:
(1)-150+250;
(2)-15+(-23);
(3)-5-65;
(4)-26-(-15);
(5)-6×(-16);
(6)
;
(7)8÷(-16);
(8)
;
100
-38
-70
-11
96
-9
-1/2
75/2
例2、判断下列计算是否正确,如果不正确,请改正。
(1)-22=(-2)2=-(-22)
(2)
(3)-13-3=-10
(4)-17+3=-20
×
×
×
×
-13-3=-16
(-2)2=-(-22)
-17+3=-14
(5)6÷(2+3)=6÷2+6÷3
(6)(2+3)÷6=2÷6+3÷6
(7)
(8)
×
√
×
×
6÷(2+3)=1.2
例4、计算:(1)(-0.02)×(-20)×(-5)×4.5;
(2)
(3)
(4)
例3、计算:(1)-2-|-3|;
(2)|-2-(-3)|
(5)-66×4-(-2.5)÷(-0.1);
(6)
;
(7)(-2)2×5-(-2)3÷4;
(8)-(3-5)+32×(1-3)
-5
1
-9
39/5
5.3
3
-289
-258
22
-16
解题技能
乘法三结合
1、积为整数结合
2、两个倒数结合
3、能约分的结合
-7
-10/7
-4
分配律
分配律反着用
分配律计算技巧
真假分配律
×
√
-29
3
4.58
-1
256
-179.25
有理数的乘方
①求n个相同因数的积的运算,叫做乘方
②正数的任何次幂都是_____;
负数的奇次幂是_____,
负数的偶次幂是_____
幂
指数
底数
a·a·a····
·a
n个
=
正数
负数
正数
1.(-1)2n
=
(-1)2n+1
=
-1n
=
(-1)n
=
(-a)2n
=
(-a)2n+1=
若a>0,则-a
n
____0;若a>0,则(-a)n
的符号是什么?(1)a2___0
(-a)3=______
(-a)4=_____
(2)a2=4,则a=_____;
(-a)2=4,则a=_____
±2
±2
≥
-a3
a4
1
-1
-1
当n为奇数时-1当n为偶数时1
<
2.平方是它本身的数有__________
3.立方是它本身的数有__________
4.某种细胞每过30分钟便由1个分裂成2个。经过5小时后一个细胞可以分裂成_____个细胞。
5.比较大小
0,1
0,1,-1
1024
6.2×32和(2×3)2有什么区别?各等于什么?
7.32和23有什么区别?各等于什么?
8.-34和(-3)4有什么区别?各等于什么?
9.
10.若0<a<1,则
之间的大小关系为(
)
A.
B.
C.
D.不能确定大小
有理数的混合运算顺序:先乘方,再乘除,最后加减。有括号,先算括号里面的;同级运算,应从左往右运。
做题时注意先观察题目整体特点,能简算的简算。
达标计算:
(3)
(4)
(5)
1.某一出租车一天下午以鼓楼为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下:+9、3、5、+4、8、+6、3、6、4、+10
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
2.已知:
互为相反数
求:
的值
达标试题:
星期
一
二
三
四
五
六
每股涨跌
+4
+4.5
-1
-2.5
-6
+2
3.小红爸爸上星期六买进某公司股票1000股,每股27元,上表为本周内每日该股票的涨跌情况。(单位:元)
(1)通过上表你认为星期三收盘时,每股是多少?
(2)本周内每股最高是多少?最低是多少元?
(3)已知小红爸爸买进股票时付了1.5‰的手续费,卖出时还需付成交额1.5‰的手续费和1‰的交易税,如果小红爸爸在星期六收盘时将全部股票卖出,你对他的收益情况怎样评价?
解:(1)27+4+4.5+(-1)=34.5
(2)27+4+4.5=35.5;27+4+4.5+(-1)+(-2.5)+(-6)+2=28.
(3)28×1000-[28×1000×﹙1.5‰+1‰﹚+27×1000×﹙1+1.5‰﹚]=28000-[70+27000+40.5]=28000-27110.5=889.5
答:(1)每股是34.5元
(2)每股最高是35.5元,最低是28元。
(3)星期六收盘时将全部股票卖出,盈利889.5元。
谢
谢
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
