2.1.1倾斜角与斜率(共19张PPT)
文档属性
| 名称 | 2.1.1倾斜角与斜率(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
2.1.1 直线的倾斜角与斜率
第二章 直线和圆的方程
学习目标
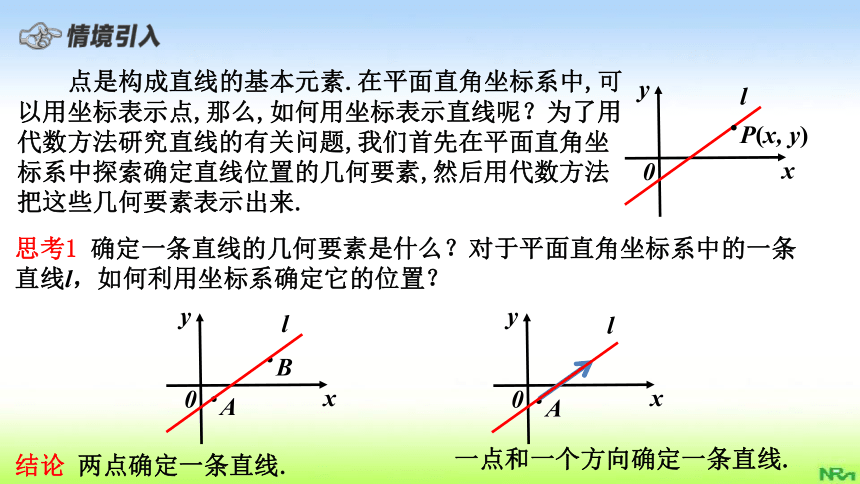
点是构成直线的基本元素.在平面直角坐标系中,可以用坐标表示点,那么,如何用坐标表示直线呢?为了用代数方法研究直线的有关问题,我们首先在平面直角坐标系中探索确定直线位置的几何要素,然后用代数方法把这些几何要素表示出来.
0
x
y
l
.P(x,
y)
思考1
确定一条直线的几何要素是什么?对于平面直角坐标系中的一条直线l,如何利用坐标系确定它的位置?
0
x
y
.A
0
x
y
.A
.B
l
l
结论
两点确定一条直线.
一点和一个方向确定一条直线.
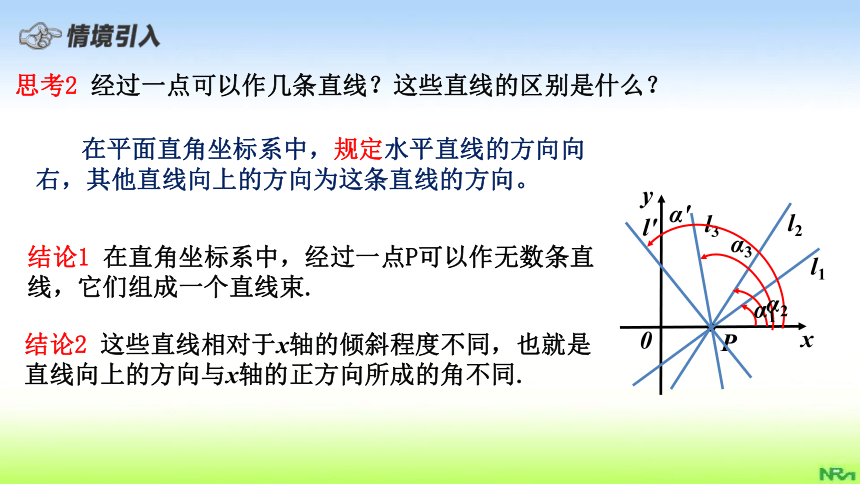
思考2
经过一点可以作几条直线?这些直线的区别是什么?
l2
0
x
y
.P
l1
l3
l'
α3
α'
α2
α1
结论1
在直角坐标系中,经过一点P可以作无数条直线,它们组成一个直线束.
结论2
这些直线相对于x轴的倾斜程度不同,也就是直线向上的方向与x轴的正方向所成的角不同.
在平面直角坐标系中,规定水平直线的方向向右,其他直线向上的方向为这条直线的方向。
新知探究
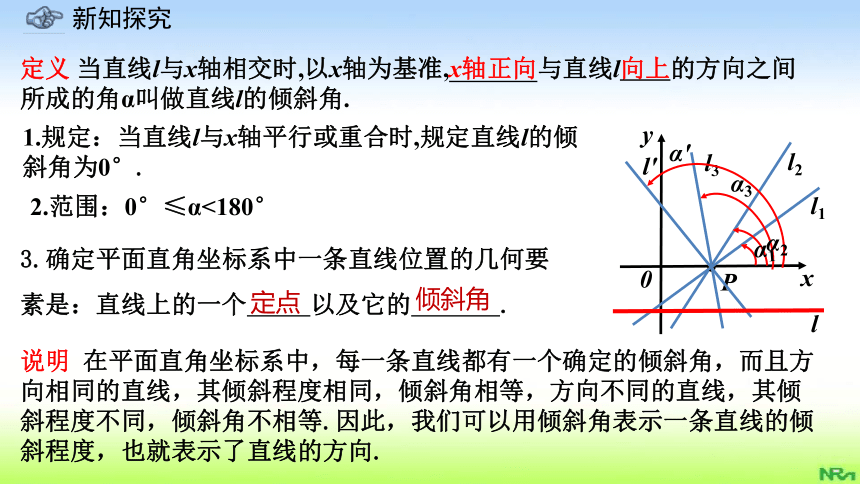
定义
当直线l与x轴相交时,以x轴为基准,x轴正向与直线l向上的方向之间所成的角α叫做直线l的倾斜角.
l2
0
x
y
.P
l1
l3
l'
α3
α'
α2
α1
l
1.规定:当直线l与x轴平行或重合时,规定直线l的倾斜角为0°.
2.范围:0°≤α<180°
3.确定平面直角坐标系中一条直线位置的几何要素是:直线上的一个
以及它的
.
定点
倾斜角
说明
在平面直角坐标系中,每一条直线都有一个确定的倾斜角,而且方向相同的直线,其倾斜程度相同,倾斜角相等,方向不同的直线,其倾斜程度不同,倾斜角不相等.因此,我们可以用倾斜角表示一条直线的倾斜程度,也就表示了直线的方向.
1.下列图中表示直线倾斜角为( )
C
3.直线x=1的倾斜角α=
.
小试牛刀
90°
2.给出下列命题:
①任何一条直线都有唯一的倾斜角;
②若α是直线l的倾斜角,且sinα=
,则α=450
;
③倾斜角为00的直线只有一条,即x轴;
④一条直线的倾斜角可以为-300.其中真命题的序号是_____.
①
思考1
在平面直角坐标系中,设直线l的倾斜角为.已知直线l经过O(0,0),P(,1),O,P的坐标有什么关系?
新知探究
设P1(x1,y1),
P2(x2,y2)(其中x1≠x2),是直线l上的两点.由两点确定一条直线可知,直线l由点P1,
P2唯一确定.所以,可以推断,直线l的倾斜角与两点P1,
P2的坐标有内在联系.
0
x
y
.
P1(x1,y1)
.
P2(x2,y2)
l
0
x
y
.
.
P(,1)
l
α
tan
思考2
在平面直角坐标系中,设直线l的倾斜角为.
如果直线l经过P1(-1,1),P2(,0),P1,
P2的坐标又有什么关系?
0
x
y
.
P1(-1,1)
l
.
P2(,0)
α
α
P
tan
思考3
在平面直角坐标系中,设直线l的倾斜角为.
如果直线l经过两点P1(x1,y1),p2(x2,y2),(x1x2),那么与P1,
P2的坐标又有怎样的关系?
tan
tan
结论:直线l的倾斜角为直线l上的两点P1(x1,y1),
p2(x2,y2)(x1x2)
的坐标有如下关系:
tan
0
x
y
.
P1(x1,y1)
.
P2(x2,y2)
l
成立,tan
思考4
如果直线l经过两点P1(x1,y1),
P2(x2,y2),x1x2
,当直线l
与x轴平行或重合时,上述式子还成立吗?为什么?
新知探究
定义
把一条直线的倾斜角的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即
k=tan
()
90°
0
(0,+∞)
(-∞,0)
说明1.斜率与倾斜角的对应关系
2.用斜率可以表示直线的倾斜程度,进而表示直线的方向.
新知探究
定义
把一条直线的倾斜角的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即
k=tan
()
如果直线l过两点P1(x1,y1),
P2(x2,y2),(x1x2),那么直线l的斜率公式
k
(x1x2)
点睛:1.运用公式的前提是x1≠x2,即直线不与x轴垂直.
2.斜率公式与P1,P2在直线上的位置无关,在直线上任取两点,得到的斜率是相同的.
3.需注意公式中横、纵坐标之差的顺序,也可以写成
即下标的顺序一致.
思考6
当直线l
与y轴平行或重合时,上述公式还成立吗?为什么?
0
x
y
.
P1(x1,y1)
.
P2(x2,y2)
l
不成立,当时,式子没有意义
无关
思考5
已知直线上两点A(a1,a1),
B(b2,b2),运用上述公式计算直线AB的斜率,与A,
B两点的顺序有关吗?
小试牛刀
√
×
×
×
450
D
新知探究
思考
直线的方向向量与斜率之间有什么关系?
结论1
若直线l的斜率为k,它的一个方向向量的坐标为(x,y)则
k
结论2
若直线l的斜率为k,则它的一个方向向量的坐标为(1,k).
0
x
y
.
P1(x1,y1)
.
P2(x2,y2)
l
典例解析
例1
如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
点拨
应用斜率公式时应先判定两定点的横坐标是否相等,若相等,直线垂直于x轴,斜率不存在;若不相等,再代入斜率公式求解;若含有参数,常常需要进行分类讨论.
1.若直线l经过第二、第四象限,则直线l的倾斜角范围是( )
A.0°≤α<90°
B.90°≤α<180°
C.90°<α<180°
D.0°<α<180°
当堂检测
3.过点P(-2,m),Q(m,4)的直线的斜率为1,那么m的值为( )
A.1或4
B.4
C.1或3
D.1
C
A
D
课堂小结
1、直线的倾斜角的定义
2、直线的斜率的定义
3、过两点的斜率公式
当直线
l
与x轴相交时,
我们取x轴作为基准,
x轴正向与直线
l
向上
方向之间所成的角α
叫做直线
l
的倾斜角.
一条直线的倾斜角 的正切值叫做这条
直线的斜率.
4、
直线的方向向量与斜率之间的关系
k
2.1.1 直线的倾斜角与斜率
第二章 直线和圆的方程
学习目标
点是构成直线的基本元素.在平面直角坐标系中,可以用坐标表示点,那么,如何用坐标表示直线呢?为了用代数方法研究直线的有关问题,我们首先在平面直角坐标系中探索确定直线位置的几何要素,然后用代数方法把这些几何要素表示出来.
0
x
y
l
.P(x,
y)
思考1
确定一条直线的几何要素是什么?对于平面直角坐标系中的一条直线l,如何利用坐标系确定它的位置?
0
x
y
.A
0
x
y
.A
.B
l
l
结论
两点确定一条直线.
一点和一个方向确定一条直线.
思考2
经过一点可以作几条直线?这些直线的区别是什么?
l2
0
x
y
.P
l1
l3
l'
α3
α'
α2
α1
结论1
在直角坐标系中,经过一点P可以作无数条直线,它们组成一个直线束.
结论2
这些直线相对于x轴的倾斜程度不同,也就是直线向上的方向与x轴的正方向所成的角不同.
在平面直角坐标系中,规定水平直线的方向向右,其他直线向上的方向为这条直线的方向。
新知探究
定义
当直线l与x轴相交时,以x轴为基准,x轴正向与直线l向上的方向之间所成的角α叫做直线l的倾斜角.
l2
0
x
y
.P
l1
l3
l'
α3
α'
α2
α1
l
1.规定:当直线l与x轴平行或重合时,规定直线l的倾斜角为0°.
2.范围:0°≤α<180°
3.确定平面直角坐标系中一条直线位置的几何要素是:直线上的一个
以及它的
.
定点
倾斜角
说明
在平面直角坐标系中,每一条直线都有一个确定的倾斜角,而且方向相同的直线,其倾斜程度相同,倾斜角相等,方向不同的直线,其倾斜程度不同,倾斜角不相等.因此,我们可以用倾斜角表示一条直线的倾斜程度,也就表示了直线的方向.
1.下列图中表示直线倾斜角为( )
C
3.直线x=1的倾斜角α=
.
小试牛刀
90°
2.给出下列命题:
①任何一条直线都有唯一的倾斜角;
②若α是直线l的倾斜角,且sinα=
,则α=450
;
③倾斜角为00的直线只有一条,即x轴;
④一条直线的倾斜角可以为-300.其中真命题的序号是_____.
①
思考1
在平面直角坐标系中,设直线l的倾斜角为.已知直线l经过O(0,0),P(,1),O,P的坐标有什么关系?
新知探究
设P1(x1,y1),
P2(x2,y2)(其中x1≠x2),是直线l上的两点.由两点确定一条直线可知,直线l由点P1,
P2唯一确定.所以,可以推断,直线l的倾斜角与两点P1,
P2的坐标有内在联系.
0
x
y
.
P1(x1,y1)
.
P2(x2,y2)
l
0
x
y
.
.
P(,1)
l
α
tan
思考2
在平面直角坐标系中,设直线l的倾斜角为.
如果直线l经过P1(-1,1),P2(,0),P1,
P2的坐标又有什么关系?
0
x
y
.
P1(-1,1)
l
.
P2(,0)
α
α
P
tan
思考3
在平面直角坐标系中,设直线l的倾斜角为.
如果直线l经过两点P1(x1,y1),p2(x2,y2),(x1x2),那么与P1,
P2的坐标又有怎样的关系?
tan
tan
结论:直线l的倾斜角为直线l上的两点P1(x1,y1),
p2(x2,y2)(x1x2)
的坐标有如下关系:
tan
0
x
y
.
P1(x1,y1)
.
P2(x2,y2)
l
成立,tan
思考4
如果直线l经过两点P1(x1,y1),
P2(x2,y2),x1x2
,当直线l
与x轴平行或重合时,上述式子还成立吗?为什么?
新知探究
定义
把一条直线的倾斜角的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即
k=tan
()
90°
0
(0,+∞)
(-∞,0)
说明1.斜率与倾斜角的对应关系
2.用斜率可以表示直线的倾斜程度,进而表示直线的方向.
新知探究
定义
把一条直线的倾斜角的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即
k=tan
()
如果直线l过两点P1(x1,y1),
P2(x2,y2),(x1x2),那么直线l的斜率公式
k
(x1x2)
点睛:1.运用公式的前提是x1≠x2,即直线不与x轴垂直.
2.斜率公式与P1,P2在直线上的位置无关,在直线上任取两点,得到的斜率是相同的.
3.需注意公式中横、纵坐标之差的顺序,也可以写成
即下标的顺序一致.
思考6
当直线l
与y轴平行或重合时,上述公式还成立吗?为什么?
0
x
y
.
P1(x1,y1)
.
P2(x2,y2)
l
不成立,当时,式子没有意义
无关
思考5
已知直线上两点A(a1,a1),
B(b2,b2),运用上述公式计算直线AB的斜率,与A,
B两点的顺序有关吗?
小试牛刀
√
×
×
×
450
D
新知探究
思考
直线的方向向量与斜率之间有什么关系?
结论1
若直线l的斜率为k,它的一个方向向量的坐标为(x,y)则
k
结论2
若直线l的斜率为k,则它的一个方向向量的坐标为(1,k).
0
x
y
.
P1(x1,y1)
.
P2(x2,y2)
l
典例解析
例1
如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
点拨
应用斜率公式时应先判定两定点的横坐标是否相等,若相等,直线垂直于x轴,斜率不存在;若不相等,再代入斜率公式求解;若含有参数,常常需要进行分类讨论.
1.若直线l经过第二、第四象限,则直线l的倾斜角范围是( )
A.0°≤α<90°
B.90°≤α<180°
C.90°<α<180°
D.0°<α<180°
当堂检测
3.过点P(-2,m),Q(m,4)的直线的斜率为1,那么m的值为( )
A.1或4
B.4
C.1或3
D.1
C
A
D
课堂小结
1、直线的倾斜角的定义
2、直线的斜率的定义
3、过两点的斜率公式
当直线
l
与x轴相交时,
我们取x轴作为基准,
x轴正向与直线
l
向上
方向之间所成的角α
叫做直线
l
的倾斜角.
一条直线的倾斜角 的正切值叫做这条
直线的斜率.
4、
直线的方向向量与斜率之间的关系
k
