人教版 六年级数学上册8运用数形结合探索规律 课件(22张PPT)
文档属性
| 名称 | 人教版 六年级数学上册8运用数形结合探索规律 课件(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
第1课时 运用数形结合探索规律
六年级数学上册(RJ) 教学课件
8 数学广角—数与形
8 数学广角—数与形
……
1.夜市路边的一排彩灯按下面的规律排列。
按上面彩灯的规律,你能算出第2020盏灯是什么颜色吗?
2020÷(2+3+4)=224(组)……4(盏)
答:第2020盏灯是黄色。
01
复习导入
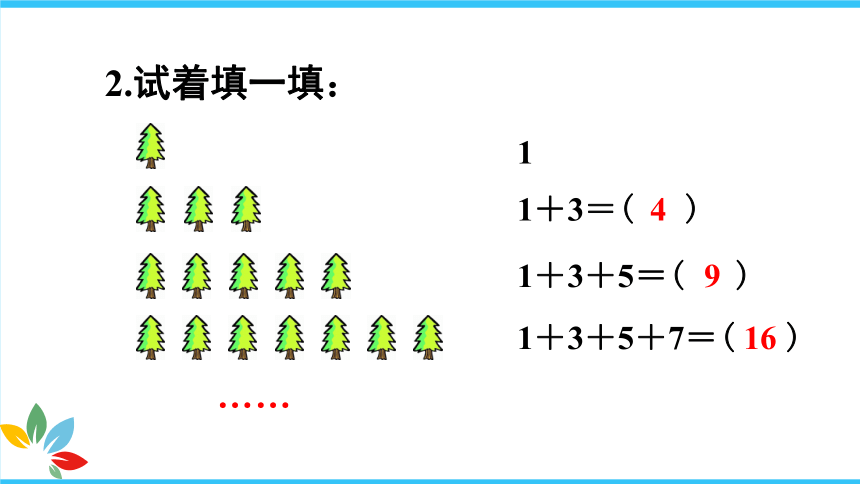
2.试着填一填:
……
1
1+3=( )
1+3+5=( )
1+3+5+7=( )
4
9
16
1=( )2
1+3=( )2
1+3+5=( )2
1+3+5+7=( )2
1
2
3
4
02
探究新知
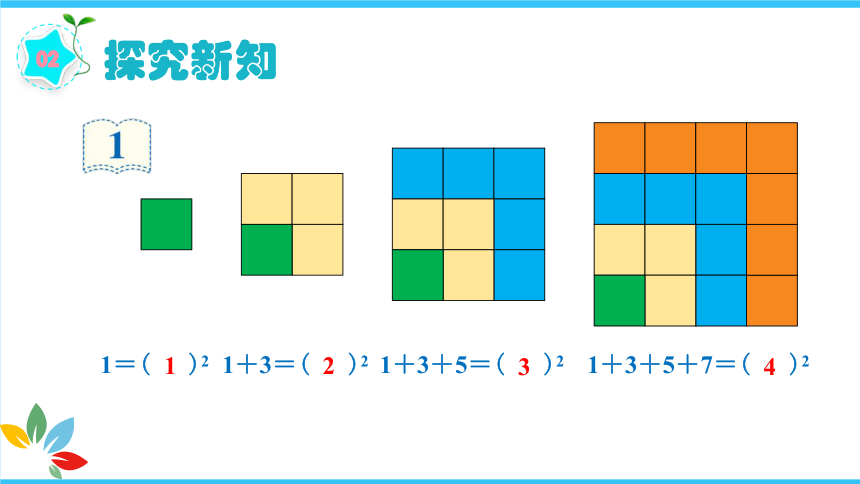
观察一下,上面的图和下面的算式有什么关系?
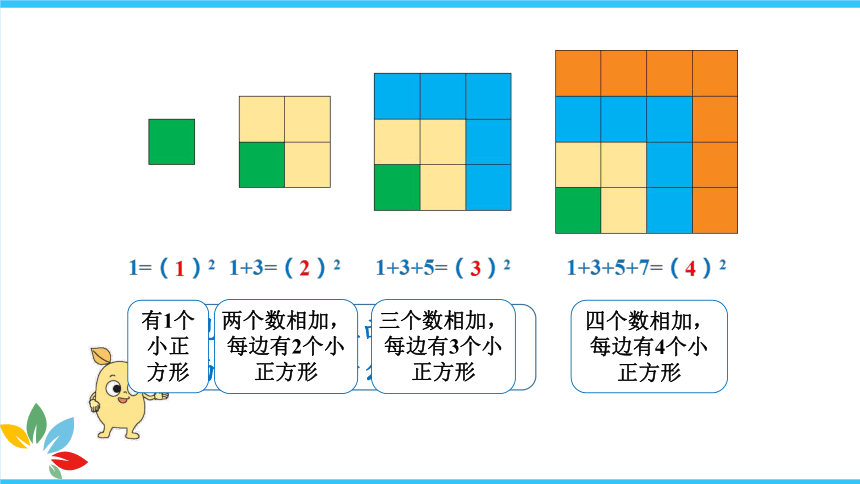
有1个小正方形
两个数相加,每边有2个小正方形
三个数相加,每边有3个小正方形
四个数相加,每边有4个小正方形
1=( )2
1
1+3=( )2
2
1+3+5=( )2
3
1+3+5+7=( )2
4
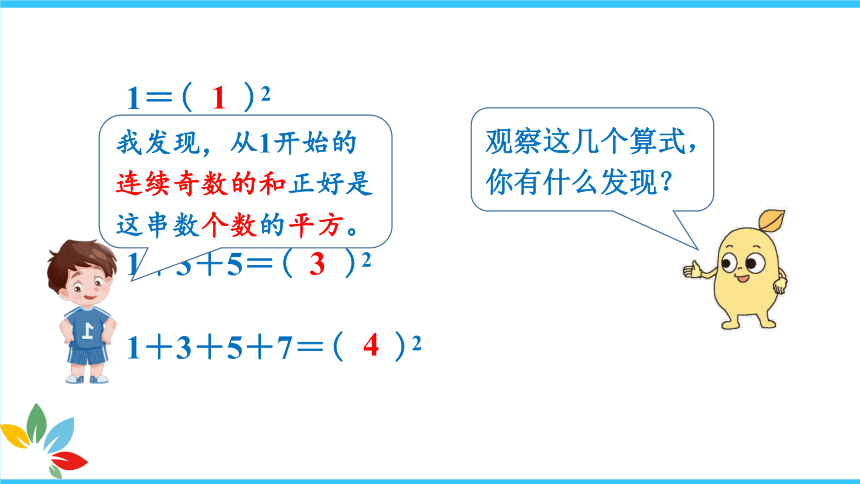
观察这几个算式,你有什么发现?
我发现,从1开始的连续奇数的和正好是这串数个数的平方。
我发现:算式左边的加数是每个正方形图左下角的小正方形和其他 “ ”图形中所包含的小正方形个数之和,正好等于每个正方形图中每列小正方形个数的平方。
你能利用规律直接写一写吗?如果有困难,可以画图来帮助。
1+3+5+7=( )2
1+3+5+7+9+11+13=( )2
____________________________ = 92
4
7
1+3+5+7+9+11+13+15+17
1 2 3 4 5 6 7
总结规律
1= 12 1+3= 22 1+3+5= 32 1+3+5+7= 42
1.加数都是从1开始连续奇数相加的。
2.和都能写成一个数的平方,我们称这样的数为平方数或正方形数。
3.第n个算式有n个加数,和是n的平方。
1+3+5+7+5+3+1=( )
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
1.请根据例1的结论算一算。
(教材P108“做一做”第1题)
25
85
4个奇数
42
32
+
3个奇数
7个奇数
72
62
+
6个奇数
03
学以致用
2.下面每个图中各有多少个红色小正方形和多少个蓝色小正方形?
(教材P108“做一做”第2题)
照这样接着画下去,第6个图形有多少个红色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
红色: 1 2 3 4
蓝色: 8 10 12 14
第6个图形中有:6个红色小正方形,18个蓝色小正方形;
第10个图形中有:10个红色小正方形,26个蓝色小正方形;
道理:
任意两个相邻的图中,红色相差1个,蓝色相差2个。
红色: 1 2 3 4
蓝色: 8 10 12 14
3.下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释这其中的道理吗?(教材P109“练习二十二”第1题)
32-1 =8 52-32 =16 72-52 =24
32-1 =8 52-32 =16 72-52 =24
3行3列
共8个
5行5列
共16个
7行7列
共24个
外圈:小正方形个数
内圈:小正方形行、列数
1行1列
3行3列
5行5列
外圈行(列)数的平方-内圈行(列)数的平方=外圈小正方形的个数
第5个图形:
所以第5个图形最外圈有40个小正方形。
11行11列共40个小正方形
外圈:
9行9列
内圈:
112
92
-
= 40
15
21
28
4.(教材P109“练习二十二”第2题)
请你根据上面图形与数的规律接着画一画,填一填。
第10个数是55。
如果不画,这样排列下去,第10个数是多少?
提示:
第1个数是1,对应的圆片数是1个;
第2个数是3,对应的圆片数是1+2=3(个);
第3个数是6,对应的圆片数是1+2+3=6(个);
第4个数是10,对应的圆片数是1+2+3+4=10(个);
……
第n个数就是从1加到n,即1+2+3+4+……+n= (个)。
1
3
4
6
9
9
16
12
5.下面每个三角形图各是由多少个小三角形组成的?如果小三角形的边长为1,每个三角形图的周长分别是多少?每个三角形图包含小三角形的个数与这个三角形图的周长之间有什么样的关系?(教材P110“练习二十二”第3题)
04
课堂小结
总结规律
从1开始的连续奇数的和正好是这列数个数的平方。
第1课时 运用数形结合探索规律
六年级数学上册(RJ) 教学课件
8 数学广角—数与形
8 数学广角—数与形
……
1.夜市路边的一排彩灯按下面的规律排列。
按上面彩灯的规律,你能算出第2020盏灯是什么颜色吗?
2020÷(2+3+4)=224(组)……4(盏)
答:第2020盏灯是黄色。
01
复习导入
2.试着填一填:
……
1
1+3=( )
1+3+5=( )
1+3+5+7=( )
4
9
16
1=( )2
1+3=( )2
1+3+5=( )2
1+3+5+7=( )2
1
2
3
4
02
探究新知
观察一下,上面的图和下面的算式有什么关系?
有1个小正方形
两个数相加,每边有2个小正方形
三个数相加,每边有3个小正方形
四个数相加,每边有4个小正方形
1=( )2
1
1+3=( )2
2
1+3+5=( )2
3
1+3+5+7=( )2
4
观察这几个算式,你有什么发现?
我发现,从1开始的连续奇数的和正好是这串数个数的平方。
我发现:算式左边的加数是每个正方形图左下角的小正方形和其他 “ ”图形中所包含的小正方形个数之和,正好等于每个正方形图中每列小正方形个数的平方。
你能利用规律直接写一写吗?如果有困难,可以画图来帮助。
1+3+5+7=( )2
1+3+5+7+9+11+13=( )2
____________________________ = 92
4
7
1+3+5+7+9+11+13+15+17
1 2 3 4 5 6 7
总结规律
1= 12 1+3= 22 1+3+5= 32 1+3+5+7= 42
1.加数都是从1开始连续奇数相加的。
2.和都能写成一个数的平方,我们称这样的数为平方数或正方形数。
3.第n个算式有n个加数,和是n的平方。
1+3+5+7+5+3+1=( )
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
1.请根据例1的结论算一算。
(教材P108“做一做”第1题)
25
85
4个奇数
42
32
+
3个奇数
7个奇数
72
62
+
6个奇数
03
学以致用
2.下面每个图中各有多少个红色小正方形和多少个蓝色小正方形?
(教材P108“做一做”第2题)
照这样接着画下去,第6个图形有多少个红色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
红色: 1 2 3 4
蓝色: 8 10 12 14
第6个图形中有:6个红色小正方形,18个蓝色小正方形;
第10个图形中有:10个红色小正方形,26个蓝色小正方形;
道理:
任意两个相邻的图中,红色相差1个,蓝色相差2个。
红色: 1 2 3 4
蓝色: 8 10 12 14
3.下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释这其中的道理吗?(教材P109“练习二十二”第1题)
32-1 =8 52-32 =16 72-52 =24
32-1 =8 52-32 =16 72-52 =24
3行3列
共8个
5行5列
共16个
7行7列
共24个
外圈:小正方形个数
内圈:小正方形行、列数
1行1列
3行3列
5行5列
外圈行(列)数的平方-内圈行(列)数的平方=外圈小正方形的个数
第5个图形:
所以第5个图形最外圈有40个小正方形。
11行11列共40个小正方形
外圈:
9行9列
内圈:
112
92
-
= 40
15
21
28
4.(教材P109“练习二十二”第2题)
请你根据上面图形与数的规律接着画一画,填一填。
第10个数是55。
如果不画,这样排列下去,第10个数是多少?
提示:
第1个数是1,对应的圆片数是1个;
第2个数是3,对应的圆片数是1+2=3(个);
第3个数是6,对应的圆片数是1+2+3=6(个);
第4个数是10,对应的圆片数是1+2+3+4=10(个);
……
第n个数就是从1加到n,即1+2+3+4+……+n= (个)。
1
3
4
6
9
9
16
12
5.下面每个三角形图各是由多少个小三角形组成的?如果小三角形的边长为1,每个三角形图的周长分别是多少?每个三角形图包含小三角形的个数与这个三角形图的周长之间有什么样的关系?(教材P110“练习二十二”第3题)
04
课堂小结
总结规律
从1开始的连续奇数的和正好是这列数个数的平方。
