人教版 六年级数学上册9 总复习 比和百分数课件(30张PPT)
文档属性
| 名称 | 人教版 六年级数学上册9 总复习 比和百分数课件(30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 14:50:25 | ||
图片预览






文档简介
(共29张PPT)
第2课时 比和百分数
六年级数学上册(RJ) 教学课件
9 总复习
9 总复习
今天这节课就对这些知识进行系统复习。
01
复习导入
你还记得我们都学习了哪些有关比和百分数的知识吗?
学习了比和百分数的意义、比的基本性质及其应用、百分数的读写法等。
比
比和分数、除法的关系
比的意义
两个数相除,又叫做两个数的比。
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
比的基本性质
各部分
名称
比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。
02
知识回顾
百分数
读百分数时,先读百分数中的分母:“%”读作“百分之……”,再读分子。
百分数的读法
百分数的意义
表示两个数之间的倍数关系,后面不能写单位名称。
百分数的写法
通常不写成分数形式,在原来的分子后面加上百分号“%”。
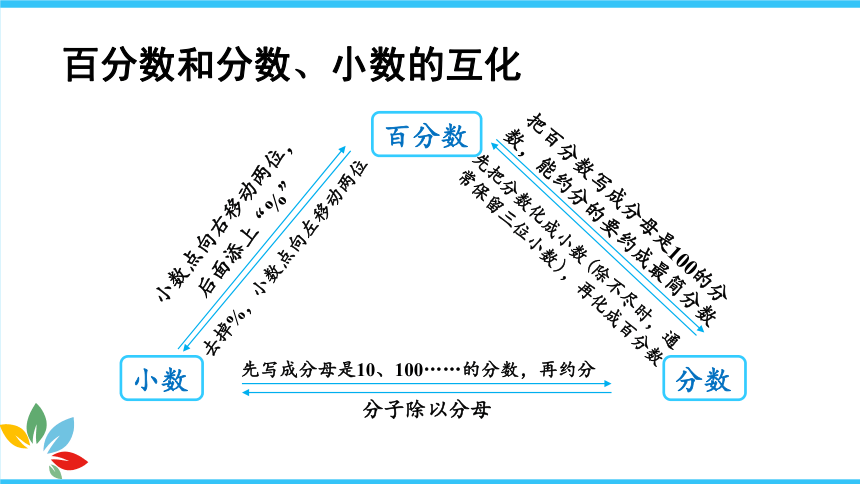
百分数和分数、小数的互化
百分数和分数、小数的互化
小数
分数
百分数
小数点向右移动两位,后面添上“%”
去掉%,小数点向左移动两位
把百分数写成分母是100的分数,能约分的要约成最简分数
先把分数化成小数(除不尽时,通常保留三位小数),再化成百分数
先写成分母是10、100……的分数,再约分
分子除以分母
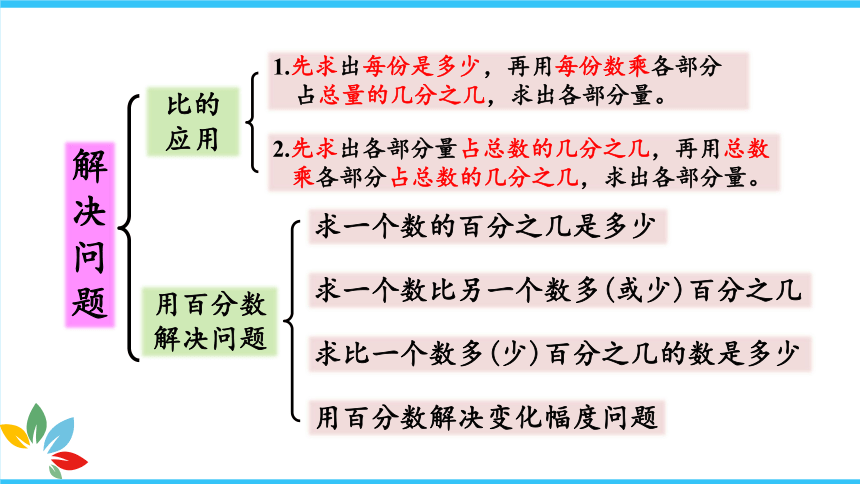
解决问题
比的应用
1.先求出每份是多少,再用每份数乘各部分占总量的几分之几,求出各部分量。
用百分数解决问题
求一个数的百分之几是多少
求一个数比另一个数多(或少)百分之几
用百分数解决变化幅度问题
求比一个数多(少)百分之几的数是多少
2.先求出各部分量占总数的几分之几,再用总数乘各部分占总数的几分之几,求出各部分量。
1.说一说比与分数、除法有什么关系,指出下面每个比的前项、后项,并求出比值。(课本P113“总复习”第2题)
03
实战演练
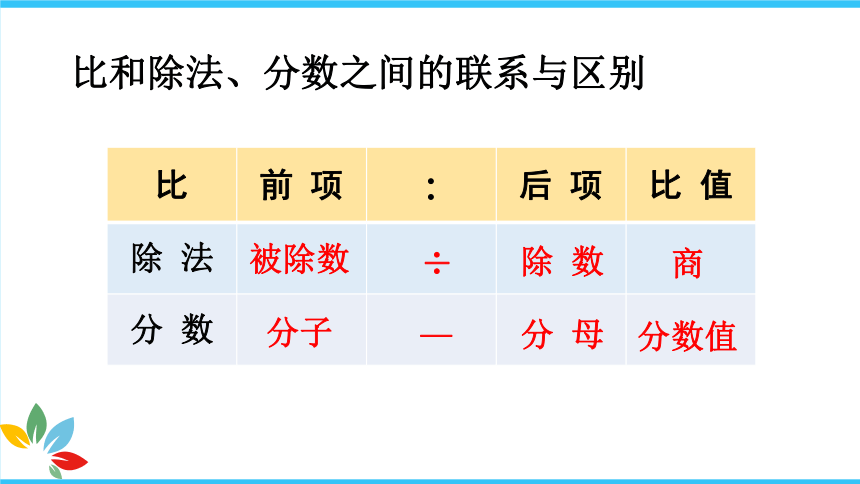
比和除法、分数之间的联系与区别
比 前 项 : 后 项 比 值
除 法
分 数
被除数
分子
÷
—
除 数
分 母
商
分数值
2:5的前项是2,后项是5。
0.6:0.3的前项是0.6,后项是0.3。
0.6÷0.3=2
2.把下面各比化成最简单的整数比。
(课本P115“练习二十三”第3题)
3.回答下列问题。你认为在解决有关分数、比和百分数的实际问题时,最关键的是什么?(课本P113“总复习”第3题)
(1)一件衬衣原价125元,现在降价 。现在售价是多少元?
现价=原价×
(元)
答:现在售价是100元。
(2)一件衬衣降价 后,售价为100元。这件衬衣原价是多少元?
原价=现价÷
(元)
答:这件衬衣原价是125元。
(3)一件衬衣原价125元,现在降价20%。现在售价是多少元?
现价=原价×(1-20%)
125×(1-20%)=100(元)
答:现在售价100元。
(4)一件衬衣降价20%后,售价为100元。这件衬衣原价是多少元?
原价=现价÷(1-20%)
100÷(1-20%)=125(元)
答:这件衬衣原价是125元。
答:这双皮鞋售价是180元。
(5)一件衬衣售价为100元,一条长裤的价格是这件衬衣的150%,这条长裤的价钱又是一双皮鞋的 。这双皮鞋售价是多少元?
一条长裤的价格=一件衬衣的价格×150%
(元)
一双皮鞋的价格=一条长裤的价格÷
答:这条长裤的售价是150元。
(6)一件衬衣售价为100元,一条长裤的价钱和这件衬衣的价钱之比是3:2。这条长裤的售价是多少元?
(元)
一条长裤的价钱=一件衬衣的价钱×
在解决有关分数、比和百分数的实际问题时,最关键的是确定单位“1”的量,并明确单位“1”的量是已知还是未知的。
4.(1)五年级同学收集了165个易拉罐,六年级同学比五年级多收集了 。六年级收集了多少个易拉罐?
(课本P116“练习二十三”第8题)
答:六年级收集了195个易拉罐。
(个)
六年级同学收集的个数=五年级同学收集的个数×
(2)四年级比六年级少收集了 ,四年级收集了多少个易拉罐?
答:四年级收集了130个易拉罐。
(个)
四年级同学收集的个数=六年级同学收集的个数×
比:
①意义:两个数相除叫做两个数的比。
②各部分名称:比号前面的数叫做比的前项,比号
后面的数叫做比的后项。比的前项
除以后项所得的商,叫做比值。
③和分数、除法的关系:
④基本性质:比的前项和后项同时乘或除以相同的
数(0除外),比值不变。
04
深化记忆
百分数:
①意义:表示一个数是另一个数的百分之几,
后面不能写单位名称。
②读法:读百分数时,先读百分数中的分母:
“%”读作“百分之…”,再读分子。
③写法:通常不写成分数形式,在原来的分子
后面加上百分号“%”。
④百分数和分数、小数的互化
小数
分数
百分数
小数点向右移动两位,后面添上“%”
去掉%,小数点向左移动两位
把百分数写成分母是100的分数,能约分的要约成最简分数
先把分数化成小数(除不尽时,通常保留三位小数),再化成百分数
先写成分母是10、100……的分数,再约分
分子除以分母
百分数和分数、小数的互化
按比分配问题的解题方法:
方法一:
先求出每份是多少,再用每份数乘各部分
占总量的几分之几,求出各部分量。
方法二:
先求出各部分量占总数的几分之几,再用
总数乘各部分占总数的几分之几,求出各部分
量。
用百分数解决问题:
求一个数的百分之几是多少:
“求一个数的百分之几是多少”的解题方
法与“求一个数的几分之几是多少”的解题方
法相同,都是用乘法计算,即都是先找到单位
“1”的量,然后用这个单位“1”的量乘百分
之几。
求一个数比另一个数多(或少)百分之几:
“求一个数比另一个数多(或少)百分之几,与求
一个数比另一个数多(或少)几分之几的解题方法相同,
只是把分数换成了百分数。
1.可以先求多(或少)的部分,再求多(或少)的部分
是另一个数的百分之几:多(或少)的量÷单位 “1”的量
=多(或少)的百分之几;
2.也可以先求一个数是另外一个数的百分之几,再
求比另外一个数多(或少)百分之几。
求比一个数多(或少)百分之几的数
是多少:
方法一:先找出表示单位“1”的量,然后
求出多(或少)的具体数量,再与单位“1”的量
相加(或减);
方法二:先找出表示单位“1”的量,然后
求出单位“1”的量与多(或少)的量所对应的百
分比的和(或差),再用单位“1”的量乘这个和
(或差)。
用百分数解决变化幅度问题:
在解答“已知一个数量的两次增减变化幅度,即
先减少(或增加)百分之几,再增加(或减少)百分之几,
求最后变化幅度”的问题时,可以用假设法,把单位
“1”设为一个具体的数量或“1”来解答。
按1来解答时,最后的变化幅度为“[ 1-1×(1-
减少幅度)×(1+增加幅度)]÷1 ”或“[1- 1×(1+
增加幅度)×(1-减少幅度)]÷1”所得的百分数。
第2课时 比和百分数
六年级数学上册(RJ) 教学课件
9 总复习
9 总复习
今天这节课就对这些知识进行系统复习。
01
复习导入
你还记得我们都学习了哪些有关比和百分数的知识吗?
学习了比和百分数的意义、比的基本性质及其应用、百分数的读写法等。
比
比和分数、除法的关系
比的意义
两个数相除,又叫做两个数的比。
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
比的基本性质
各部分
名称
比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。
02
知识回顾
百分数
读百分数时,先读百分数中的分母:“%”读作“百分之……”,再读分子。
百分数的读法
百分数的意义
表示两个数之间的倍数关系,后面不能写单位名称。
百分数的写法
通常不写成分数形式,在原来的分子后面加上百分号“%”。
百分数和分数、小数的互化
百分数和分数、小数的互化
小数
分数
百分数
小数点向右移动两位,后面添上“%”
去掉%,小数点向左移动两位
把百分数写成分母是100的分数,能约分的要约成最简分数
先把分数化成小数(除不尽时,通常保留三位小数),再化成百分数
先写成分母是10、100……的分数,再约分
分子除以分母
解决问题
比的应用
1.先求出每份是多少,再用每份数乘各部分占总量的几分之几,求出各部分量。
用百分数解决问题
求一个数的百分之几是多少
求一个数比另一个数多(或少)百分之几
用百分数解决变化幅度问题
求比一个数多(少)百分之几的数是多少
2.先求出各部分量占总数的几分之几,再用总数乘各部分占总数的几分之几,求出各部分量。
1.说一说比与分数、除法有什么关系,指出下面每个比的前项、后项,并求出比值。(课本P113“总复习”第2题)
03
实战演练
比和除法、分数之间的联系与区别
比 前 项 : 后 项 比 值
除 法
分 数
被除数
分子
÷
—
除 数
分 母
商
分数值
2:5的前项是2,后项是5。
0.6:0.3的前项是0.6,后项是0.3。
0.6÷0.3=2
2.把下面各比化成最简单的整数比。
(课本P115“练习二十三”第3题)
3.回答下列问题。你认为在解决有关分数、比和百分数的实际问题时,最关键的是什么?(课本P113“总复习”第3题)
(1)一件衬衣原价125元,现在降价 。现在售价是多少元?
现价=原价×
(元)
答:现在售价是100元。
(2)一件衬衣降价 后,售价为100元。这件衬衣原价是多少元?
原价=现价÷
(元)
答:这件衬衣原价是125元。
(3)一件衬衣原价125元,现在降价20%。现在售价是多少元?
现价=原价×(1-20%)
125×(1-20%)=100(元)
答:现在售价100元。
(4)一件衬衣降价20%后,售价为100元。这件衬衣原价是多少元?
原价=现价÷(1-20%)
100÷(1-20%)=125(元)
答:这件衬衣原价是125元。
答:这双皮鞋售价是180元。
(5)一件衬衣售价为100元,一条长裤的价格是这件衬衣的150%,这条长裤的价钱又是一双皮鞋的 。这双皮鞋售价是多少元?
一条长裤的价格=一件衬衣的价格×150%
(元)
一双皮鞋的价格=一条长裤的价格÷
答:这条长裤的售价是150元。
(6)一件衬衣售价为100元,一条长裤的价钱和这件衬衣的价钱之比是3:2。这条长裤的售价是多少元?
(元)
一条长裤的价钱=一件衬衣的价钱×
在解决有关分数、比和百分数的实际问题时,最关键的是确定单位“1”的量,并明确单位“1”的量是已知还是未知的。
4.(1)五年级同学收集了165个易拉罐,六年级同学比五年级多收集了 。六年级收集了多少个易拉罐?
(课本P116“练习二十三”第8题)
答:六年级收集了195个易拉罐。
(个)
六年级同学收集的个数=五年级同学收集的个数×
(2)四年级比六年级少收集了 ,四年级收集了多少个易拉罐?
答:四年级收集了130个易拉罐。
(个)
四年级同学收集的个数=六年级同学收集的个数×
比:
①意义:两个数相除叫做两个数的比。
②各部分名称:比号前面的数叫做比的前项,比号
后面的数叫做比的后项。比的前项
除以后项所得的商,叫做比值。
③和分数、除法的关系:
④基本性质:比的前项和后项同时乘或除以相同的
数(0除外),比值不变。
04
深化记忆
百分数:
①意义:表示一个数是另一个数的百分之几,
后面不能写单位名称。
②读法:读百分数时,先读百分数中的分母:
“%”读作“百分之…”,再读分子。
③写法:通常不写成分数形式,在原来的分子
后面加上百分号“%”。
④百分数和分数、小数的互化
小数
分数
百分数
小数点向右移动两位,后面添上“%”
去掉%,小数点向左移动两位
把百分数写成分母是100的分数,能约分的要约成最简分数
先把分数化成小数(除不尽时,通常保留三位小数),再化成百分数
先写成分母是10、100……的分数,再约分
分子除以分母
百分数和分数、小数的互化
按比分配问题的解题方法:
方法一:
先求出每份是多少,再用每份数乘各部分
占总量的几分之几,求出各部分量。
方法二:
先求出各部分量占总数的几分之几,再用
总数乘各部分占总数的几分之几,求出各部分
量。
用百分数解决问题:
求一个数的百分之几是多少:
“求一个数的百分之几是多少”的解题方
法与“求一个数的几分之几是多少”的解题方
法相同,都是用乘法计算,即都是先找到单位
“1”的量,然后用这个单位“1”的量乘百分
之几。
求一个数比另一个数多(或少)百分之几:
“求一个数比另一个数多(或少)百分之几,与求
一个数比另一个数多(或少)几分之几的解题方法相同,
只是把分数换成了百分数。
1.可以先求多(或少)的部分,再求多(或少)的部分
是另一个数的百分之几:多(或少)的量÷单位 “1”的量
=多(或少)的百分之几;
2.也可以先求一个数是另外一个数的百分之几,再
求比另外一个数多(或少)百分之几。
求比一个数多(或少)百分之几的数
是多少:
方法一:先找出表示单位“1”的量,然后
求出多(或少)的具体数量,再与单位“1”的量
相加(或减);
方法二:先找出表示单位“1”的量,然后
求出单位“1”的量与多(或少)的量所对应的百
分比的和(或差),再用单位“1”的量乘这个和
(或差)。
用百分数解决变化幅度问题:
在解答“已知一个数量的两次增减变化幅度,即
先减少(或增加)百分之几,再增加(或减少)百分之几,
求最后变化幅度”的问题时,可以用假设法,把单位
“1”设为一个具体的数量或“1”来解答。
按1来解答时,最后的变化幅度为“[ 1-1×(1-
减少幅度)×(1+增加幅度)]÷1 ”或“[1- 1×(1+
增加幅度)×(1-减少幅度)]÷1”所得的百分数。
