2.5三角函数的应用 同步专题提升训练 2021-2022学年鲁教版(五四制)九年级数学上册(word版含答案)
文档属性
| 名称 | 2.5三角函数的应用 同步专题提升训练 2021-2022学年鲁教版(五四制)九年级数学上册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 440.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 08:25:59 | ||
图片预览

文档简介
2021-2022学年鲁教版九年级数学上册《2.5三角函数的应用》同步专题提升训练(附答案)
一、选择题
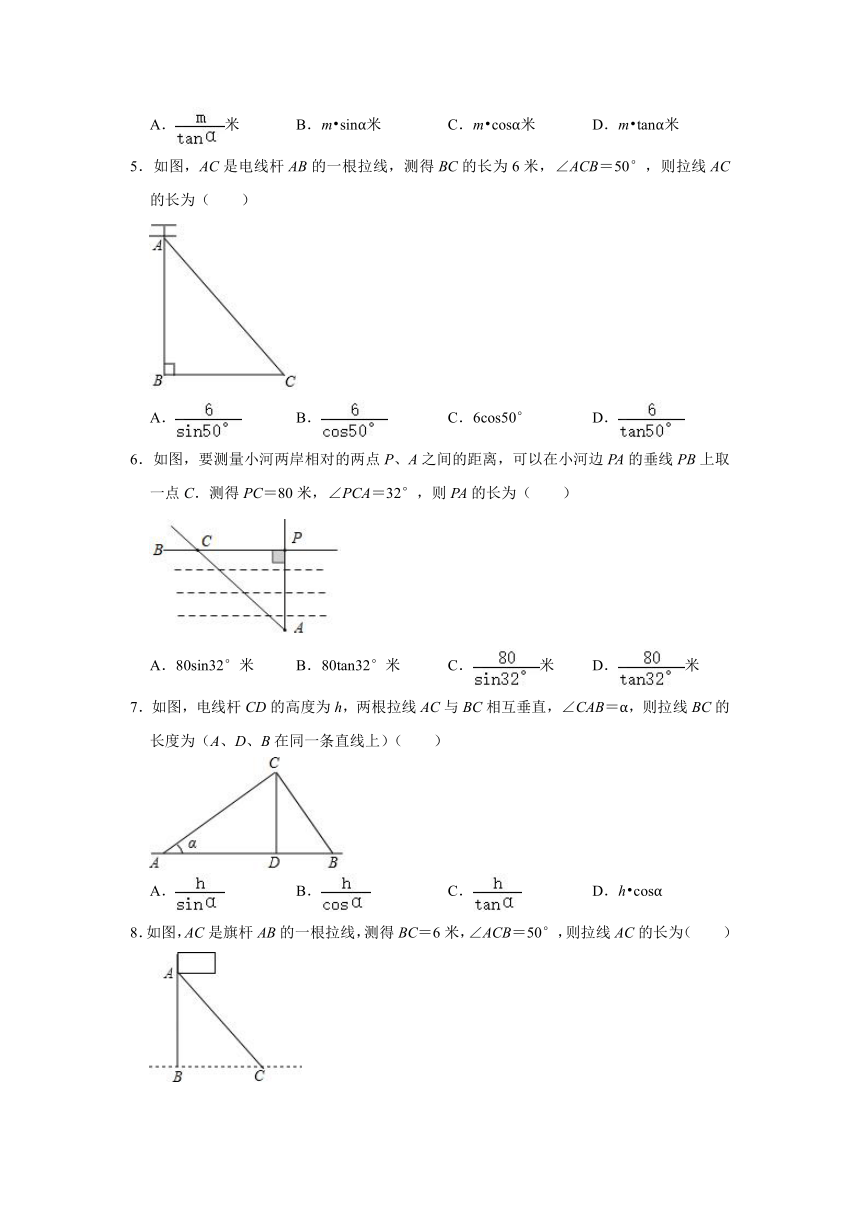
1.如图,小明利用一个锐角是30°的三角板测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度是( )
A.(15+)m
B.5m
C.15m
D.(5+)m
2.如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.30sinα米
B.米
C.30cosα米
D.米
3.如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为β,已知sinα=cosβ=,则梯子顶端上升了( )
A.1米
B.1.5米
C.2米
D.2.5米
4.如图,为了测量河两岸A、B两点间的距离,只需在与AB垂直方向的点C处测得垂线段AC=m米,若∠ACB=α,那么AB等于( )
A.米
B.m?sinα米
C.m?cosα米
D.m?tanα米
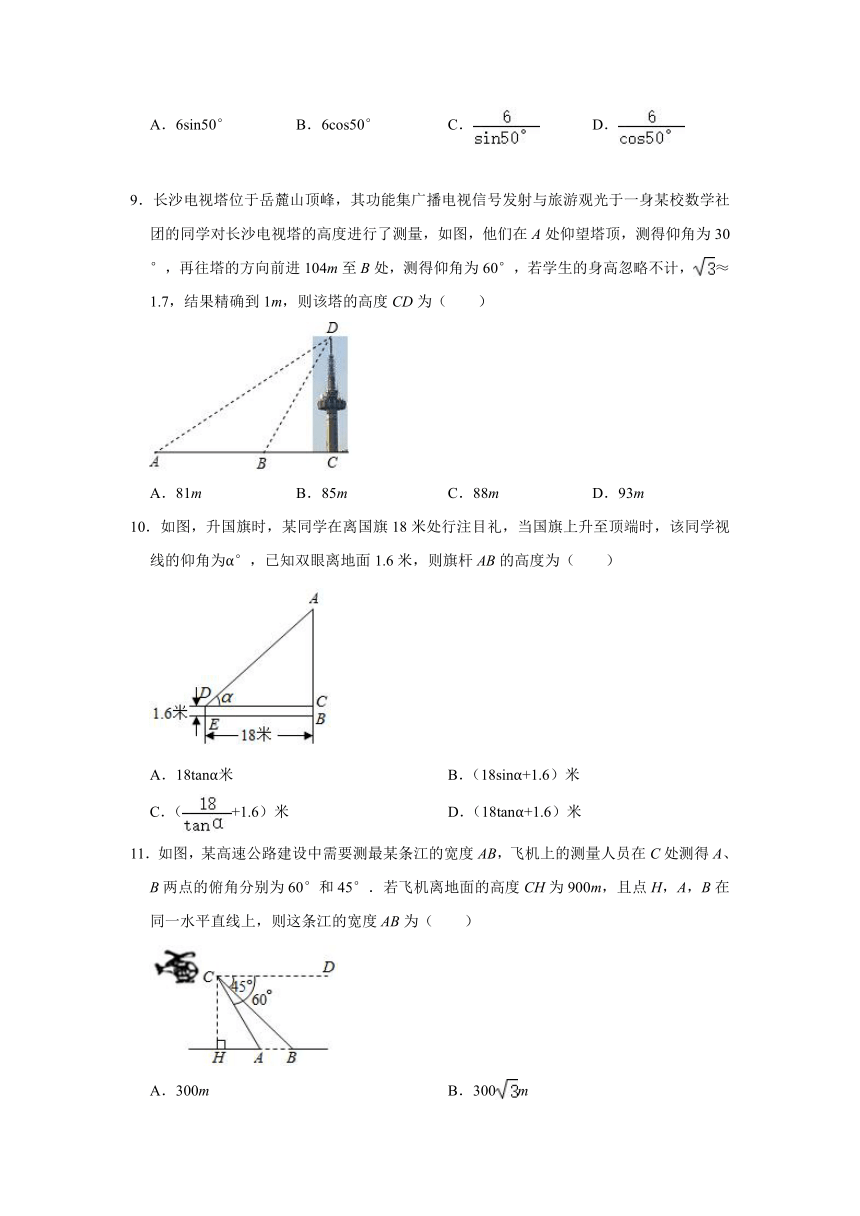
5.如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
A.
B.
C.6cos50°
D.
6.如图,要测量小河两岸相对的两点P、A之间的距离,可以在小河边PA的垂线PB上取一点C.测得PC=80米,∠PCA=32°,则PA的长为( )
A.80sin32°米
B.80tan32°米
C.米
D.米
7.如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)( )
A.
B.
C.
D.h?cosα
8.如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )
A.6sin50°
B.6cos50°
C.
D.
9.长沙电视塔位于岳麓山顶峰,其功能集广播电视信号发射与旅游观光于一身某校数学社团的同学对长沙电视塔的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往塔的方向前进104m至B处,测得仰角为60°,若学生的身高忽略不计,≈1.7,结果精确到1m,则该塔的高度CD为( )
A.81m
B.85m
C.88m
D.93m
10.如图,升国旗时,某同学在离国旗18米处行注目礼,当国旗上升至顶端时,该同学视线的仰角为α°,已知双眼离地面1.6米,则旗杆AB的高度为( )
A.18tanα米
B.(18sinα+1.6)米
C.(+1.6)米
D.(18tanα+1.6)米
11.如图,某高速公路建设中需要测最某条江的宽度AB,飞机上的测量人员在C处测得A、B两点的俯角分别为60°和45°.若飞机离地面的高度CH为900m,且点H,A,B在同一水平直线上,则这条江的宽度AB为( )
A.300m
B.300m
C.(900+300)m
D.(900﹣300)m
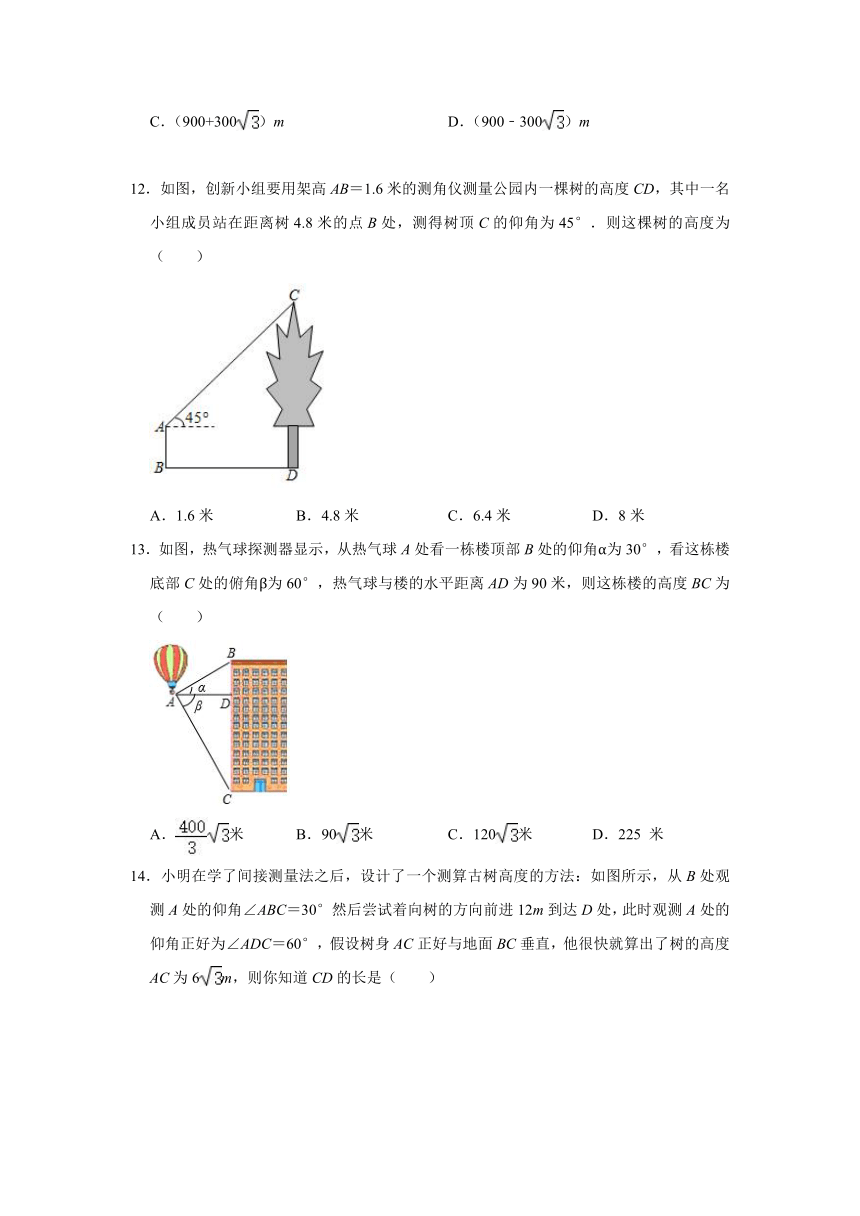
12.如图,创新小组要用架高AB=1.6米的测角仪测量公园内一棵树的高度CD,其中一名小组成员站在距离树4.8米的点B处,测得树顶C的仰角为45°.则这棵树的高度为( )
A.1.6米
B.4.8米
C.6.4米
D.8米
13.如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角α为30°,看这栋楼底部C处的俯角β为60°,热气球与楼的水平距离AD为90米,则这栋楼的高度BC为( )
A.米
B.90米
C.120米
D.225
米
14.小明在学了间接测量法之后,设计了一个测算古树高度的方法:如图所示,从B处观测A处的仰角∠ABC=30°然后尝试着向树的方向前进12m到达D处,此时观测A处的仰角正好为∠ADC=60°,假设树身AC正好与地面BC垂直,他很快就算出了树的高度AC为6m,则你知道CD的长是( )
A.4
B.5
C.6
D.12
15.如图,小明想测量数学楼DE的高度.他从距教学楼底部E点水平距离为30米的A点处出发.沿坡度的i=1:2.4的斜坡AB行走了13米,到达二楼水平平台的B处,继续行驶5米到达水平平台的C处,从C处观察教学楼顶端D的仰角为53°(点A、B、C、D、E均在同一平面内).则教学楼DE的高度约为( )(参考数据:sin53°≈0.8,cos53°≈0.6.tan53°≈)
A.22.1米
B.22.3米
C.17.1米
D.17.3米
16.“五一”期间,小明和妈妈到某景区游玩,小明想利用所学的数学知识,估测景区里的观景塔DE的高度.他从点D处的观景塔出来走到点A处.沿着斜坡AB从A点走了8米到达B点,此时回望观景塔,更显气势宏伟.在B点观察到观景塔顶端的仰角为45°且AB⊥BE,再往前走到C处,观察到观景塔顶端的仰角30°,测得BC之间的水平距离BC=10米,则观景塔的高度DE约为( )米.(=1.41,=1.73)
A.14
B.15
C.19
D.20
二、填空题
17.小明用一块含有60°(∠DAE=60°)的直角三角尺测量校园内某棵树的高度,示意图如图所示,若小明的眼睛与地面之间的垂直高度AB为1.62m,小明与树之间的水平距离BC为4m,则这棵树的高度约为
m.(结果精确到0.1m,参考数据:≈1.73)
18.如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度约为
m(结果精确到1m,≈1.7).
19.如图.AB和CD两幢楼在同一水平面上.楼AB高30米.从楼AB的顶部A测得楼CD的底部C的俯角为30°,顶部D的仰角为45°.则楼CD的高度是
米(取1.732,用四舍五入法将结果取整数).
20.已知在离地面30米的高楼窗台A处测得地面花坛中心标志物C的俯角为60°,那么这一标志物C离此栋楼房的地面距离BC为
米.
三、解答题
21.如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.(参考数据:tan31°≈0.6,tan50°≈1.2)
(1)求B,C两点间的距离(结果精确到1m);
(2)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
22.为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途经C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:≈1.41,≈1.73)
23.如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:,且AB=26米.
(1)求坡顶与地面的距离BE的长.
(2)为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33).
24.如图,小李从西边山脚的点A走了300m后到达山顶C,已知∠A=30°,东边山坡的坡度tanB=.
(1)求山顶C离地面的高度.
(2)求B、C的距离.
25.放风筝是大家喜爱的一种运动.星期天的上午小明(A)和小丽(B)在振羽广场的水平地面上放风筝,结果风筝在空中D处纠缠在一起,如图所示.此时,小明的风筝线AD与水平线的夹角为30°,小丽的风筝线BD与水平线的夹角为60°,小明与小丽之间的距离AB为20米.已知点
A、B、C在同一条直线上,∠ACD=90°,求点D到地面的距离DC为多少米?(本题中风筝线均视为线段,,结果精确到0.1米)
参考答案
1.解:由题意可得,四边形ABCD是矩形,BC=15m,AB=1.5m,
∴BC=AD=15m,AB=CD=1.5m,
在Rt△ADE中,∠EAD=30°,AD=15m,
∴DE=AD?tan∠EAD=15×=5(m),
∴CE=CD+DE=(5+1.5)(m).
故选:D.
2.解:由图可知,在△ABC中,AC⊥BC,
∴sinα==,
∴BC=30sinα米.
故选:A.
3.解:如图所示,
在Rt△ABC中,AC=sinα×AB==6(米);
在Rt△DEC中,DC=cosβ×DE==6(米),EC===8(米);
∴AE=EC﹣AC=8﹣6=2(米).
故选:C.
4.解:∵BA⊥AC,
∴∠BAC=90°,
∵AC=m米,∠ACB=α,
∴tanα=,
∴AB=m?tanα,
故选:D.
5.解:∵∠ABC=90°,∠ACB=60°,BC=6m,
∴cos50°==,
∴AC=.
故选:B.
6.解:由题意得:∠APC=90°,
在Rt△APC中,PC=80米,∠PCA=32°,
∵tan∠PCA=,
∴PA=PC?tan∠PCA=80tan32°(米);
故选:B.
7.解:∵∠CAD+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠CAD=∠BCD,
在Rt△BCD中,∵cos∠BCD=,
∴BC==,
故选:B.
8.解:∵BC=6米,∠ACB=50°,
∴拉线AC的长为=,
故选:D.
9.解:根据题意得:∠A=30°,∠DBC=60°,DC⊥AC,
∴∠ADB=∠DBC﹣∠A=30°,
∴∠ADB=∠A=30°,
∴BD=AB=104m,
∴CD=BD?sin60°=104×=52≈88(m),
解法二:根据AC=CD,BCCD,然后长度一减得到AB,再根据AB为104,可求CD.
故选:C.
10.解:由题意知,BE=18米,DE=1.6米,
四边形DEBC为矩形,BC=DE=1.6米,CD=BE=18米,
在Rt△ADC中,
∵tan∠α=,
∴AC=18tanα,
∴AB=AC+BC=(18tanα+1.6)米,
故选:D.
11.解:由图可得,
∠CHA=90°,∠HCA=30°,∠HCB=45°,
∵CH=900m,
∴HA=CH?tan30°=900×=300(m),HB=CH?tan45°=900×1=900(m),
∴AB=HB﹣HA=(900﹣300)(m),
故选:D.
12.解:如图,过点A作AE⊥CD,垂足为E.则四边形ABDE是矩形,DE=AB=1.6米,AE=BD=4.8米,
在Rt△ACE中,AE=4.8米,∠CAE=45°,
∴CE=AE=4.8米.
∴CD=CE+DE=4.8+1.6=6.4(米).
故树的高度约为6.4米.故选:C.
13.解:由题意可得,
α=30°,β=60°,AD=90米,∠ADC=∠ADB=90°,
∴在Rt△ADB中,α=30°,AD=90米,
∴tanα=,
∴BD=30(米),
在Rt△ADC中,β=60°,AD=90米,
∴tanβ=,
∴CD=90(米),
∴BC=BD+CD=30+90=120(米),
即这栋楼的高度BC是120米.
故选:C.
14.解:∵∠ADC=60°,∠ABC=30°,
∴∠DAB=60°﹣30°=30°,
∴AD=DB=12m,
在Rt△ACD中,
∴CD=AD=6m;
∴CD的长是6m;
故选:C.
15.解:过点B作BM⊥AE于点M,延长BC交DE于N,
∵斜坡AB的坡度(或坡比)i=1:2.4,AB=13米,
∴设BM=x(米),则AM=2.4x(米).
在Rt△ABM中,
∵AM2+BM2=AB2,即x2+(2.4x)2=132,解得x=5,
∴BM=5米,AM=12米,
∴ME=30﹣12=18(米),
∴CN=18﹣5=13(米).
在Rt△CDN中,
∵∠DCN=53°,
∴DN=CN?tan53°≈13×=(米),
∵四边形BMEN是矩形,
∴EN=BM=5(米),
∴DE=EN+DN=5+=22.3(米).
故选:B.
16.解:作BF⊥DE于F,AH⊥BF于H,
∵∠EBF=45°,
∴∠ABH=45°,
∴AH=BH=8×=4,
在Rt△ECF中,tan∠ECF=,
则CF=EF,
在Rt△EBF中,∠EBF=45°,
∴BF=EF,
由题意得,EF﹣EF=10,
解得,EF=5+5,
则DE=EF+DF=5+5+4≈19,
故选:C.
17.解:∵AB⊥BC,DC⊥BC,AD∥BC,
∴四边形ABCD是矩形,
∵BC=4m,AB=1.62m,
∴AD=BC=4m,DC=AB=1.62m,
在Rt△ACD中,
∵∠CAD=30°,AD=4m,
∴CD=AD?tan60°=4×=4(m),
∴CE=ED+DC=4+1.62≈8.5(m)
答:这棵树的高度约为8.5m.
故答案为:8.5.
18.解:如图,过A作AE⊥CD于E,
则AB=CE,
在△ACE中,∵∠AEC=90°,∠CAE=30°,EC=AB=21米,
∴AC=21×2=42(米),
∴AE===21≈35.7(米),
在Rt△ADE中,∵∠AED=90°,∠DAE=45°,
∴AE=DE=35.7米,
∴乙楼DC=CE+ED=21+35.7=56.7≈57(米).
答:乙楼的高约为57米.
19.解:如图,过点A作AE⊥DC于点E,
则四边形ABCE是矩形,
∴CE=AB=30米,
∴AE==30(米),
∵∠D=∠DAE=45°,
∴DE=AE=30(米),
∴CD=CE+DE=30+30≈82(米),
答:楼CD的高度为约82米.
故答案为:82.
20.解:根据题意得到AB=30米,∠BAC=30°,
∵AB⊥BC,
∴BC=AB?tan30°=30×=10米,
∴标志物C离此栋楼房的地面距离BC为10米,
故答案为10.
21.解:(1)在Rt△ACD
中,,
∴,
在Rt△ABD
中,,
∴.
∴BC=BD﹣CD=20(m);
∴B,C
两点间的距离为BD﹣CD=20(m);
(2)此轿车的速度,
所以此轿车在该路段没有超速.
22.解:(1)过点C作AB的垂线CD,垂足为D,
∵AB⊥CD,sin30°=,BC=80千米,
∴CD=BC?sin30°=80×(千米),
AC=(千米),
AC+BC=80+40(千米),
答:开通隧道前,汽车从A地到B地要走80+40千米;
(2)∵cos30°=,BC=80(千米),
∴BD=BC?cos30°=80×(千米),
∵tan45°=,CD=40(千米),
∴AD=(千米),
∴AB=AD+BD=40+40≈40+40×1.73=109.2(千米),
∴汽车从A地到B地比原来少走多少路程为:(AC+BC)﹣AB=136.4﹣109.2=27.2(千米).
答:汽车从A地到B地比原来少走的路程为27.2千米.
23.解:(1)设AE=5x米,
∵斜坡AB的坡比为i=1:,
∴BE=12x米,
由勾股定理得,AE2+BE2=AB2,即(5x)2+(12x)2=262,
解得,x=2,
∴BE=12x=24(米);
(2)过点F作FG⊥AD于G,
则四边形FGEB为矩形,
∴FG=BE=24米,BF=GE,
在Rt△AFG中,∠FAG=53°,
∴AG=≈≈18.0(米),
由(1)可知,AE=10米,
∴BF=GE=AG﹣AE≈8(米),
答:BF至少是8米.
24.解:(1)过点C作CD⊥AB于D,
在Rt△ACD中,∠A=30°,AC=300m,
∴CD=AC=150(m),
答:山顶C离地面的高度为150m;
(2)在Rt△BCD中,tanB=,
∴=,即=,
解得,BD=200(m),
由勾股定理得,BC==250(m),
答:B、C的距离为250m.
25.解:如图所示:∵∠DAB=30°,∠DBC=60°,
∴∠ADB=∠DBC﹣∠DAB=30°,
∴∠DAB=∠ADB,
∴BD=BA=20m,
在Rt△DBC中,∠BCD=90°,
∠DBC=60°,BD=20m,
∴DC=BDsin∠DBC
=20×sin60°
=20×
=17.32
≈17.3(米),
答:点D到地面的距离DC约17.3米.
一、选择题
1.如图,小明利用一个锐角是30°的三角板测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度是( )
A.(15+)m
B.5m
C.15m
D.(5+)m
2.如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.30sinα米
B.米
C.30cosα米
D.米
3.如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为β,已知sinα=cosβ=,则梯子顶端上升了( )
A.1米
B.1.5米
C.2米
D.2.5米
4.如图,为了测量河两岸A、B两点间的距离,只需在与AB垂直方向的点C处测得垂线段AC=m米,若∠ACB=α,那么AB等于( )
A.米
B.m?sinα米
C.m?cosα米
D.m?tanα米
5.如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
A.
B.
C.6cos50°
D.
6.如图,要测量小河两岸相对的两点P、A之间的距离,可以在小河边PA的垂线PB上取一点C.测得PC=80米,∠PCA=32°,则PA的长为( )
A.80sin32°米
B.80tan32°米
C.米
D.米
7.如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)( )
A.
B.
C.
D.h?cosα
8.如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )
A.6sin50°
B.6cos50°
C.
D.
9.长沙电视塔位于岳麓山顶峰,其功能集广播电视信号发射与旅游观光于一身某校数学社团的同学对长沙电视塔的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往塔的方向前进104m至B处,测得仰角为60°,若学生的身高忽略不计,≈1.7,结果精确到1m,则该塔的高度CD为( )
A.81m
B.85m
C.88m
D.93m
10.如图,升国旗时,某同学在离国旗18米处行注目礼,当国旗上升至顶端时,该同学视线的仰角为α°,已知双眼离地面1.6米,则旗杆AB的高度为( )
A.18tanα米
B.(18sinα+1.6)米
C.(+1.6)米
D.(18tanα+1.6)米
11.如图,某高速公路建设中需要测最某条江的宽度AB,飞机上的测量人员在C处测得A、B两点的俯角分别为60°和45°.若飞机离地面的高度CH为900m,且点H,A,B在同一水平直线上,则这条江的宽度AB为( )
A.300m
B.300m
C.(900+300)m
D.(900﹣300)m
12.如图,创新小组要用架高AB=1.6米的测角仪测量公园内一棵树的高度CD,其中一名小组成员站在距离树4.8米的点B处,测得树顶C的仰角为45°.则这棵树的高度为( )
A.1.6米
B.4.8米
C.6.4米
D.8米
13.如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角α为30°,看这栋楼底部C处的俯角β为60°,热气球与楼的水平距离AD为90米,则这栋楼的高度BC为( )
A.米
B.90米
C.120米
D.225
米
14.小明在学了间接测量法之后,设计了一个测算古树高度的方法:如图所示,从B处观测A处的仰角∠ABC=30°然后尝试着向树的方向前进12m到达D处,此时观测A处的仰角正好为∠ADC=60°,假设树身AC正好与地面BC垂直,他很快就算出了树的高度AC为6m,则你知道CD的长是( )
A.4
B.5
C.6
D.12
15.如图,小明想测量数学楼DE的高度.他从距教学楼底部E点水平距离为30米的A点处出发.沿坡度的i=1:2.4的斜坡AB行走了13米,到达二楼水平平台的B处,继续行驶5米到达水平平台的C处,从C处观察教学楼顶端D的仰角为53°(点A、B、C、D、E均在同一平面内).则教学楼DE的高度约为( )(参考数据:sin53°≈0.8,cos53°≈0.6.tan53°≈)
A.22.1米
B.22.3米
C.17.1米
D.17.3米
16.“五一”期间,小明和妈妈到某景区游玩,小明想利用所学的数学知识,估测景区里的观景塔DE的高度.他从点D处的观景塔出来走到点A处.沿着斜坡AB从A点走了8米到达B点,此时回望观景塔,更显气势宏伟.在B点观察到观景塔顶端的仰角为45°且AB⊥BE,再往前走到C处,观察到观景塔顶端的仰角30°,测得BC之间的水平距离BC=10米,则观景塔的高度DE约为( )米.(=1.41,=1.73)
A.14
B.15
C.19
D.20
二、填空题
17.小明用一块含有60°(∠DAE=60°)的直角三角尺测量校园内某棵树的高度,示意图如图所示,若小明的眼睛与地面之间的垂直高度AB为1.62m,小明与树之间的水平距离BC为4m,则这棵树的高度约为
m.(结果精确到0.1m,参考数据:≈1.73)
18.如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度约为
m(结果精确到1m,≈1.7).
19.如图.AB和CD两幢楼在同一水平面上.楼AB高30米.从楼AB的顶部A测得楼CD的底部C的俯角为30°,顶部D的仰角为45°.则楼CD的高度是
米(取1.732,用四舍五入法将结果取整数).
20.已知在离地面30米的高楼窗台A处测得地面花坛中心标志物C的俯角为60°,那么这一标志物C离此栋楼房的地面距离BC为
米.
三、解答题
21.如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.(参考数据:tan31°≈0.6,tan50°≈1.2)
(1)求B,C两点间的距离(结果精确到1m);
(2)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
22.为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途经C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:≈1.41,≈1.73)
23.如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:,且AB=26米.
(1)求坡顶与地面的距离BE的长.
(2)为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33).
24.如图,小李从西边山脚的点A走了300m后到达山顶C,已知∠A=30°,东边山坡的坡度tanB=.
(1)求山顶C离地面的高度.
(2)求B、C的距离.
25.放风筝是大家喜爱的一种运动.星期天的上午小明(A)和小丽(B)在振羽广场的水平地面上放风筝,结果风筝在空中D处纠缠在一起,如图所示.此时,小明的风筝线AD与水平线的夹角为30°,小丽的风筝线BD与水平线的夹角为60°,小明与小丽之间的距离AB为20米.已知点
A、B、C在同一条直线上,∠ACD=90°,求点D到地面的距离DC为多少米?(本题中风筝线均视为线段,,结果精确到0.1米)
参考答案
1.解:由题意可得,四边形ABCD是矩形,BC=15m,AB=1.5m,
∴BC=AD=15m,AB=CD=1.5m,
在Rt△ADE中,∠EAD=30°,AD=15m,
∴DE=AD?tan∠EAD=15×=5(m),
∴CE=CD+DE=(5+1.5)(m).
故选:D.
2.解:由图可知,在△ABC中,AC⊥BC,
∴sinα==,
∴BC=30sinα米.
故选:A.
3.解:如图所示,
在Rt△ABC中,AC=sinα×AB==6(米);
在Rt△DEC中,DC=cosβ×DE==6(米),EC===8(米);
∴AE=EC﹣AC=8﹣6=2(米).
故选:C.
4.解:∵BA⊥AC,
∴∠BAC=90°,
∵AC=m米,∠ACB=α,
∴tanα=,
∴AB=m?tanα,
故选:D.
5.解:∵∠ABC=90°,∠ACB=60°,BC=6m,
∴cos50°==,
∴AC=.
故选:B.
6.解:由题意得:∠APC=90°,
在Rt△APC中,PC=80米,∠PCA=32°,
∵tan∠PCA=,
∴PA=PC?tan∠PCA=80tan32°(米);
故选:B.
7.解:∵∠CAD+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠CAD=∠BCD,
在Rt△BCD中,∵cos∠BCD=,
∴BC==,
故选:B.
8.解:∵BC=6米,∠ACB=50°,
∴拉线AC的长为=,
故选:D.
9.解:根据题意得:∠A=30°,∠DBC=60°,DC⊥AC,
∴∠ADB=∠DBC﹣∠A=30°,
∴∠ADB=∠A=30°,
∴BD=AB=104m,
∴CD=BD?sin60°=104×=52≈88(m),
解法二:根据AC=CD,BCCD,然后长度一减得到AB,再根据AB为104,可求CD.
故选:C.
10.解:由题意知,BE=18米,DE=1.6米,
四边形DEBC为矩形,BC=DE=1.6米,CD=BE=18米,
在Rt△ADC中,
∵tan∠α=,
∴AC=18tanα,
∴AB=AC+BC=(18tanα+1.6)米,
故选:D.
11.解:由图可得,
∠CHA=90°,∠HCA=30°,∠HCB=45°,
∵CH=900m,
∴HA=CH?tan30°=900×=300(m),HB=CH?tan45°=900×1=900(m),
∴AB=HB﹣HA=(900﹣300)(m),
故选:D.
12.解:如图,过点A作AE⊥CD,垂足为E.则四边形ABDE是矩形,DE=AB=1.6米,AE=BD=4.8米,
在Rt△ACE中,AE=4.8米,∠CAE=45°,
∴CE=AE=4.8米.
∴CD=CE+DE=4.8+1.6=6.4(米).
故树的高度约为6.4米.故选:C.
13.解:由题意可得,
α=30°,β=60°,AD=90米,∠ADC=∠ADB=90°,
∴在Rt△ADB中,α=30°,AD=90米,
∴tanα=,
∴BD=30(米),
在Rt△ADC中,β=60°,AD=90米,
∴tanβ=,
∴CD=90(米),
∴BC=BD+CD=30+90=120(米),
即这栋楼的高度BC是120米.
故选:C.
14.解:∵∠ADC=60°,∠ABC=30°,
∴∠DAB=60°﹣30°=30°,
∴AD=DB=12m,
在Rt△ACD中,
∴CD=AD=6m;
∴CD的长是6m;
故选:C.
15.解:过点B作BM⊥AE于点M,延长BC交DE于N,
∵斜坡AB的坡度(或坡比)i=1:2.4,AB=13米,
∴设BM=x(米),则AM=2.4x(米).
在Rt△ABM中,
∵AM2+BM2=AB2,即x2+(2.4x)2=132,解得x=5,
∴BM=5米,AM=12米,
∴ME=30﹣12=18(米),
∴CN=18﹣5=13(米).
在Rt△CDN中,
∵∠DCN=53°,
∴DN=CN?tan53°≈13×=(米),
∵四边形BMEN是矩形,
∴EN=BM=5(米),
∴DE=EN+DN=5+=22.3(米).
故选:B.
16.解:作BF⊥DE于F,AH⊥BF于H,
∵∠EBF=45°,
∴∠ABH=45°,
∴AH=BH=8×=4,
在Rt△ECF中,tan∠ECF=,
则CF=EF,
在Rt△EBF中,∠EBF=45°,
∴BF=EF,
由题意得,EF﹣EF=10,
解得,EF=5+5,
则DE=EF+DF=5+5+4≈19,
故选:C.
17.解:∵AB⊥BC,DC⊥BC,AD∥BC,
∴四边形ABCD是矩形,
∵BC=4m,AB=1.62m,
∴AD=BC=4m,DC=AB=1.62m,
在Rt△ACD中,
∵∠CAD=30°,AD=4m,
∴CD=AD?tan60°=4×=4(m),
∴CE=ED+DC=4+1.62≈8.5(m)
答:这棵树的高度约为8.5m.
故答案为:8.5.
18.解:如图,过A作AE⊥CD于E,
则AB=CE,
在△ACE中,∵∠AEC=90°,∠CAE=30°,EC=AB=21米,
∴AC=21×2=42(米),
∴AE===21≈35.7(米),
在Rt△ADE中,∵∠AED=90°,∠DAE=45°,
∴AE=DE=35.7米,
∴乙楼DC=CE+ED=21+35.7=56.7≈57(米).
答:乙楼的高约为57米.
19.解:如图,过点A作AE⊥DC于点E,
则四边形ABCE是矩形,
∴CE=AB=30米,
∴AE==30(米),
∵∠D=∠DAE=45°,
∴DE=AE=30(米),
∴CD=CE+DE=30+30≈82(米),
答:楼CD的高度为约82米.
故答案为:82.
20.解:根据题意得到AB=30米,∠BAC=30°,
∵AB⊥BC,
∴BC=AB?tan30°=30×=10米,
∴标志物C离此栋楼房的地面距离BC为10米,
故答案为10.
21.解:(1)在Rt△ACD
中,,
∴,
在Rt△ABD
中,,
∴.
∴BC=BD﹣CD=20(m);
∴B,C
两点间的距离为BD﹣CD=20(m);
(2)此轿车的速度,
所以此轿车在该路段没有超速.
22.解:(1)过点C作AB的垂线CD,垂足为D,
∵AB⊥CD,sin30°=,BC=80千米,
∴CD=BC?sin30°=80×(千米),
AC=(千米),
AC+BC=80+40(千米),
答:开通隧道前,汽车从A地到B地要走80+40千米;
(2)∵cos30°=,BC=80(千米),
∴BD=BC?cos30°=80×(千米),
∵tan45°=,CD=40(千米),
∴AD=(千米),
∴AB=AD+BD=40+40≈40+40×1.73=109.2(千米),
∴汽车从A地到B地比原来少走多少路程为:(AC+BC)﹣AB=136.4﹣109.2=27.2(千米).
答:汽车从A地到B地比原来少走的路程为27.2千米.
23.解:(1)设AE=5x米,
∵斜坡AB的坡比为i=1:,
∴BE=12x米,
由勾股定理得,AE2+BE2=AB2,即(5x)2+(12x)2=262,
解得,x=2,
∴BE=12x=24(米);
(2)过点F作FG⊥AD于G,
则四边形FGEB为矩形,
∴FG=BE=24米,BF=GE,
在Rt△AFG中,∠FAG=53°,
∴AG=≈≈18.0(米),
由(1)可知,AE=10米,
∴BF=GE=AG﹣AE≈8(米),
答:BF至少是8米.
24.解:(1)过点C作CD⊥AB于D,
在Rt△ACD中,∠A=30°,AC=300m,
∴CD=AC=150(m),
答:山顶C离地面的高度为150m;
(2)在Rt△BCD中,tanB=,
∴=,即=,
解得,BD=200(m),
由勾股定理得,BC==250(m),
答:B、C的距离为250m.
25.解:如图所示:∵∠DAB=30°,∠DBC=60°,
∴∠ADB=∠DBC﹣∠DAB=30°,
∴∠DAB=∠ADB,
∴BD=BA=20m,
在Rt△DBC中,∠BCD=90°,
∠DBC=60°,BD=20m,
∴DC=BDsin∠DBC
=20×sin60°
=20×
=17.32
≈17.3(米),
答:点D到地面的距离DC约17.3米.
