2021-2022学年鲁教版七年级数学上册 第一章 三角形题型专练(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版七年级数学上册 第一章 三角形题型专练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 769.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 22:00:47 | ||
图片预览


文档简介
2021-2022学年数学鲁教版七年级上册第一章三角形题型专练
一、选择题
1.下面是一位同学用三根木棒拼成的图形,其中是三角形的是(
)
A.
B.
C.
D.
2.下列图形是全等形的是(
)
A.
B.
C.
D.
3.已知三角形的两边长分别是3和7,则此三角形的第三边长可能是(
)
A.4
B.8
C.10
D.12
4.如图所示,,,,,,则等于(
)
A.120°
B.125°
C.130°
D.135°
5.若一个三角形的三个内角的度数之比为,则这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰二角形
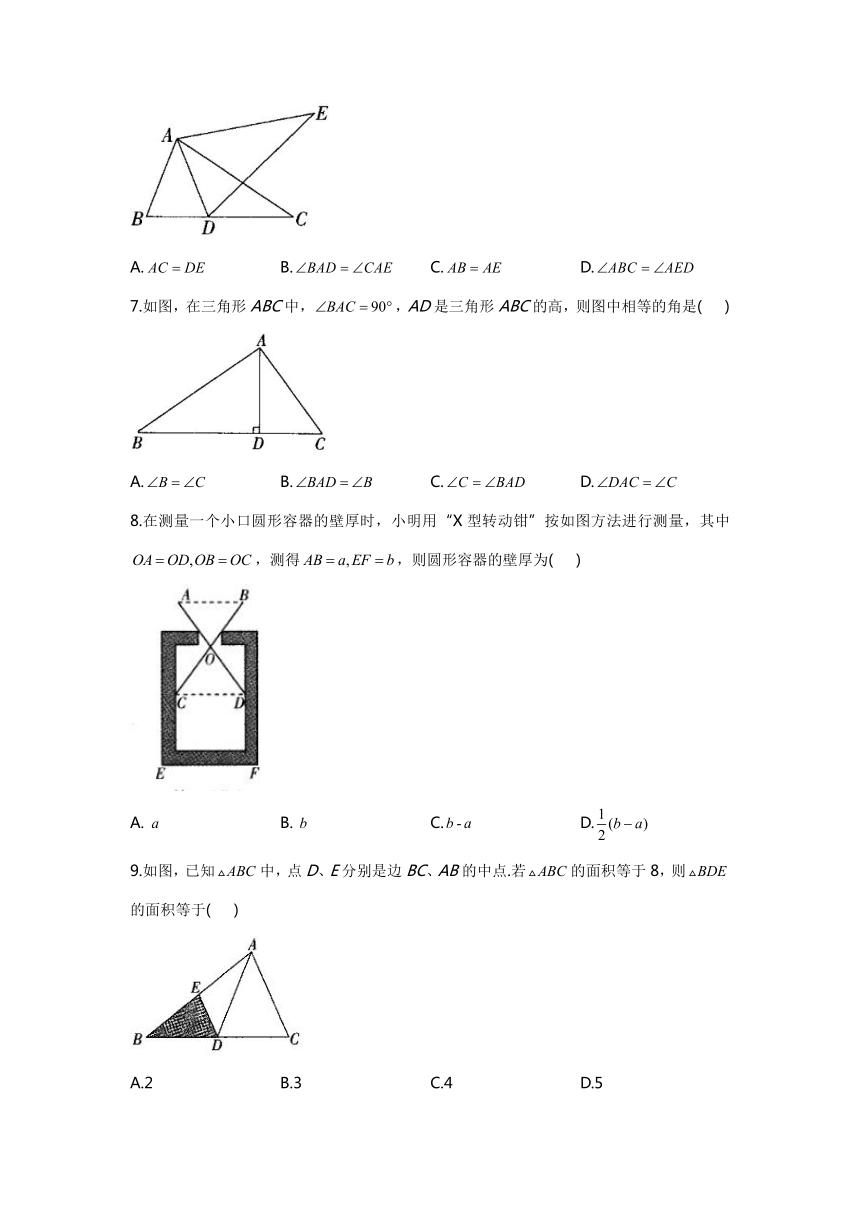
6.如图,若,则下列结论中一定成立的是(
)
A.
B.
C.
D.
7.如图,在三角形ABC中,,AD是三角形ABC的高,则图中相等的角是(
)
A.
B.
C.
D.
8.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中,测得,则圆形容器的壁厚为(
)
A.
B.
C.
D.
9.如图,已知中,点D、E分别是边BC、AB的中点.若的面积等于8,则的面积等于(
)
A.2
B.3
C.4
D.5
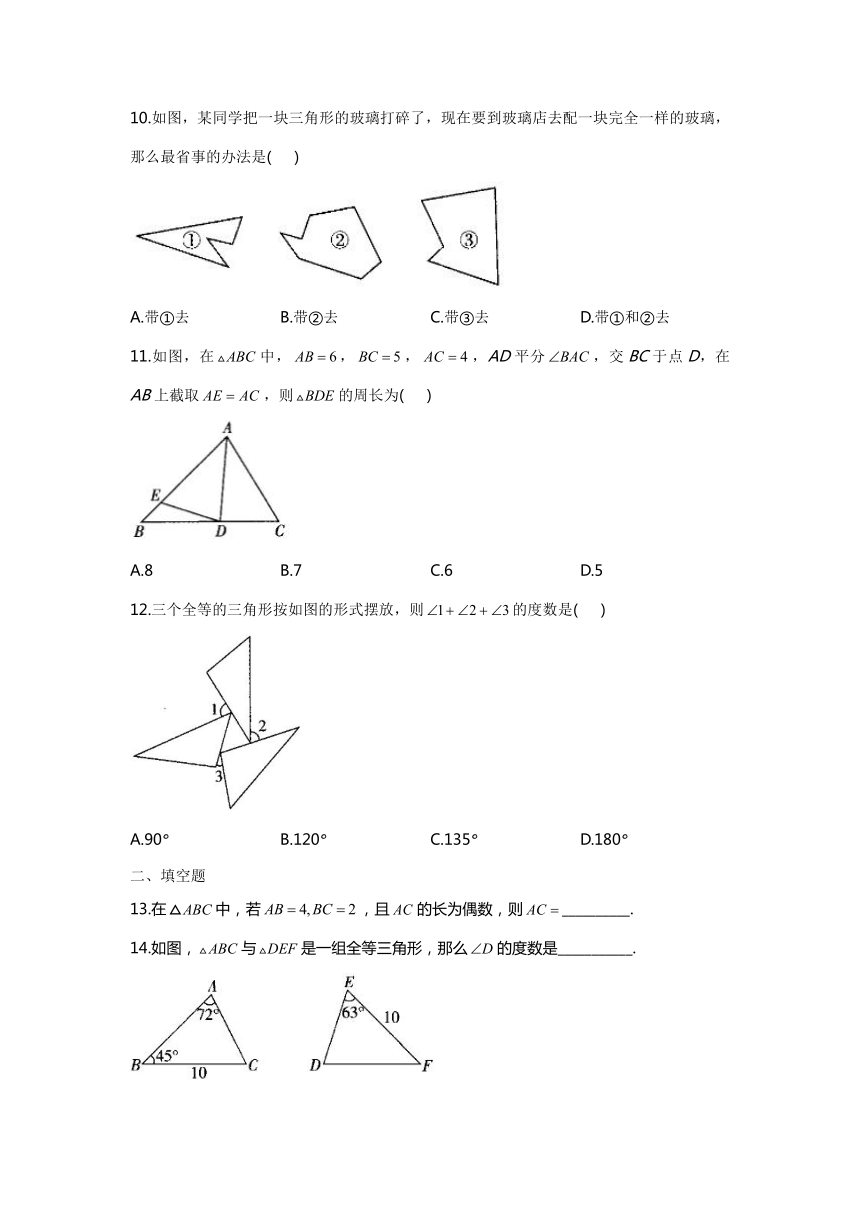
10.如图,某同学把一块三角形的玻璃打碎了,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是(
)
A.带①去
B.带②去
C.带③去
D.带①和②去
11.如图,在中,,,,AD平分,交BC于点D,在AB上截取,则的周长为(
)
A.8
B.7
C.6
D.5
12.三个全等的三角形按如图的形式摆放,则的度数是(
)
A.90°
B.120°
C.135°
D.180°
二、填空题
13.在中,若,且的长为偶数,则__________.
14.如图,与是一组全等三角形,那么的度数是___________.
15.把一副三角尺按如图所示方式放置,则图中钝角的度数是__________.
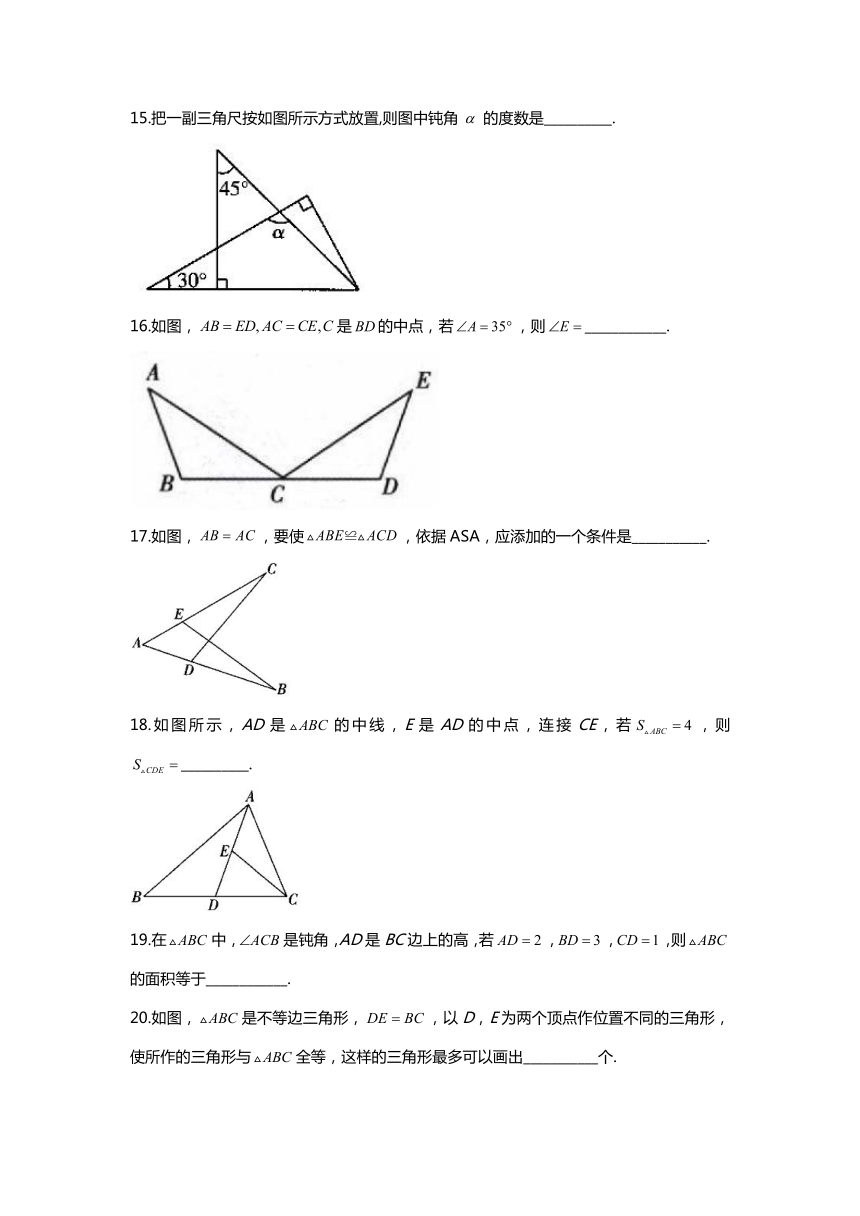
16.如图,是的中点,若,则____________.
17.如图,,要使,依据ASA,应添加的一个条件是___________.
18.如图所示,AD是的中线,E是AD的中点,连接CE,若,则__________.
19.在中,是钝角,AD是BC边上的高,若,,,则的面积等于____________.
20.如图,是不等边三角形,,以D,E为两个顶点作位置不同的三角形,使所作的三角形与全等,这样的三角形最多可以画出___________个.
21.如图,点D,C,A在同一条直线上.在中,,若,则的度数为____________.
22.如图,已知,添加下列条件中的一个:①,②,③.其中不能确定的是___________.(只填序号)
23.如图,,
,添加一个条件____________________,使得.
24.如图,已知,.给出下列条件:①;②;③;④.其中能使的条件为______________.(注:把你认为正确的序号都填上)
三、解答题
25.下图是两个全等的五边形,,,指出它们的对应顶点、对应边与对应角,并说出图中标的a,b,c,e,所表示的值.
26.如图,已知点B,C,D,E在同一条直线上,,,.求证:.
27如图,某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20m有一树C,继续前行20m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处时停止行走;
④测得DE的长为5米.
根据他们的做法,回答下列问题:
(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
28.如图,在中,AD是BC边上的高,AE是的平分线,,,求的度数.
29.已知一个等腰三角形的周长是36cm,其中一边长为8cm,求另外两边的长.
30.如图,,其中点A,B,C,D在一条直线上.
(1)若,,求的度数;
(2)若cm,cm,求AB的长.
31.如图,AC是四边形ABCD的对角线,,点E、F分别在AB、BC上,,,连接EF.
(1)求证:;
(2)若,,求的度数.
32.如图,在中(),,BC边上的中线AD把的周长分成60和40两部分,求AC和AB的长.
答案以及解析
1.答案:D
解析:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形,由此可知A,B,C不是三角形,D是三角形.故选D.
2.答案:D
解析:能够完全重合的两个图形叫做全等形.结合选项,知只有D项中的两个图形能够完全重合.故选D.
3.答案:B
解析:设第三边长为x,则由三角形三边关系得,即,故选B.
4.答案:B
解析:,,,,.,.故选B.
5.答案:A
解析:三角形三个内角的度数之比为,三个内角分别是,,.所以该三角形是锐角三角形.
6.答案:B
解析:,,,,,
,即.故B中结论正确,故选B.
7.答案:C
解析:AD是三角形ABC的高,,,,,,,故选C.
8.答案:D
解析:在△AOB和△DOC中,所以(SAS),所以,因为,所以圆形容器的壁厚为.故选D.
9.答案:A
解析:D是边BC的中点,的面积等于8,,E是边AB的中点,,故选A.
10.答案:C
解析:第①块仅保留了原三角形的一个角和部分边,不符合任何一种判定两个三角形全等的条件;第②块仅保留了原三角形的部分边,所以不符合任何一种判定两个三角形全等的条件;第③块不但保留了原三角形的两个角,还保留了其中一条边,所以符合用ASA判定两个三角形全等的条件,所以应该拿③去.故选C.
11.答案:B
解析:AD平分,.在和中,,,,,的周长为.故选B.
12.答案:D
解析:如图所示,.三个三角形是全等的,
.又,,的度数是180°.故选D.
1.3答案:4
解析:根据题意,得,即,又的长是偶数,所以.
14.答案:72°
解析:与是一组全等三角形,且,与是对应角,,,故答案为72°.
15答案:105°
解析:由三角形内角和定理,得.
16.答案:35°
解析:∵是的中点,∴.在和中,,∴,∴.
17.答案:
解析:应添加,在和中,,.
18.答案:1
解析:AD是的中线,,E是AD的中点,.
19.答案:2
解析:如图.,,,又AD是BC边上的高,,的面积.
20.答案:4
解析:如图,可以作出这样的三角形4个.
21.答案:20°
解析:,.,,,.
22.答案:②
解析:若添加①,则可由“AAS”判定;若添加②,则不能判定;若添加③,则可由“SAS”判定.
23.答案:(或或或)
解析:因为,所以.因为,所以.当添加或时,可根据“AAS”判定;当添加或时,可根据“ASA"判定.
24.答案:①③④
解析:,,即,又,要判定,需添加的条件为①;③;④.故填①③④.
25.答案:对应顶点:A和G,E和F,D和J,C和I,B和H;
对应边:AB和GH,AE和GF,ED和FJ,DC和JI,BC和HI;
对应角:和,和,和,和,和.
两个五边形全等,
,,,,.
26.答案:证明:,,即.
在和中,,
.
27.答案:(1)河宽AB是5米.
(2)由题意知,在和中,,
,.
故河宽AB就是测得的DE的长,因此他们的做法是正确的.
28.答案:AD是BC边上的高,,
,
,
,
AE是的平分线,
,
.
29.答案:若腰长为8cm,则底边长为(cm),此时,不能构成三角形,即这个等腰三角形的腰长不能为8cm.
若底边长为8cm,则腰长为(cm),
此时能构成三角形,所以这个等腰三角形的底边长为8cm,两腰长都是14cm,
即另外两边的长都是14cm.
综上可知,该等腰三角形的另外两边的长都为14cm.
30.答案:(1),.
,
,
.
(2),,
,即.
cm,cm,
(cm),
cm.
31.答案:(1)证明:在和中,
,
,
.
(2),,
,
,
.
32.答案:AD是BC边上的中线,,
设,,则,
,.
分为两种情况:
①,,则,,
解得,,即,;
②,,则,,
解得,,即,,,
由于,故不符合三角形的三边关系.
综上所述,,.
一、选择题
1.下面是一位同学用三根木棒拼成的图形,其中是三角形的是(
)
A.
B.
C.
D.
2.下列图形是全等形的是(
)
A.
B.
C.
D.
3.已知三角形的两边长分别是3和7,则此三角形的第三边长可能是(
)
A.4
B.8
C.10
D.12
4.如图所示,,,,,,则等于(
)
A.120°
B.125°
C.130°
D.135°
5.若一个三角形的三个内角的度数之比为,则这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰二角形
6.如图,若,则下列结论中一定成立的是(
)
A.
B.
C.
D.
7.如图,在三角形ABC中,,AD是三角形ABC的高,则图中相等的角是(
)
A.
B.
C.
D.
8.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中,测得,则圆形容器的壁厚为(
)
A.
B.
C.
D.
9.如图,已知中,点D、E分别是边BC、AB的中点.若的面积等于8,则的面积等于(
)
A.2
B.3
C.4
D.5
10.如图,某同学把一块三角形的玻璃打碎了,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是(
)
A.带①去
B.带②去
C.带③去
D.带①和②去
11.如图,在中,,,,AD平分,交BC于点D,在AB上截取,则的周长为(
)
A.8
B.7
C.6
D.5
12.三个全等的三角形按如图的形式摆放,则的度数是(
)
A.90°
B.120°
C.135°
D.180°
二、填空题
13.在中,若,且的长为偶数,则__________.
14.如图,与是一组全等三角形,那么的度数是___________.
15.把一副三角尺按如图所示方式放置,则图中钝角的度数是__________.
16.如图,是的中点,若,则____________.
17.如图,,要使,依据ASA,应添加的一个条件是___________.
18.如图所示,AD是的中线,E是AD的中点,连接CE,若,则__________.
19.在中,是钝角,AD是BC边上的高,若,,,则的面积等于____________.
20.如图,是不等边三角形,,以D,E为两个顶点作位置不同的三角形,使所作的三角形与全等,这样的三角形最多可以画出___________个.
21.如图,点D,C,A在同一条直线上.在中,,若,则的度数为____________.
22.如图,已知,添加下列条件中的一个:①,②,③.其中不能确定的是___________.(只填序号)
23.如图,,
,添加一个条件____________________,使得.
24.如图,已知,.给出下列条件:①;②;③;④.其中能使的条件为______________.(注:把你认为正确的序号都填上)
三、解答题
25.下图是两个全等的五边形,,,指出它们的对应顶点、对应边与对应角,并说出图中标的a,b,c,e,所表示的值.
26.如图,已知点B,C,D,E在同一条直线上,,,.求证:.
27如图,某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20m有一树C,继续前行20m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处时停止行走;
④测得DE的长为5米.
根据他们的做法,回答下列问题:
(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
28.如图,在中,AD是BC边上的高,AE是的平分线,,,求的度数.
29.已知一个等腰三角形的周长是36cm,其中一边长为8cm,求另外两边的长.
30.如图,,其中点A,B,C,D在一条直线上.
(1)若,,求的度数;
(2)若cm,cm,求AB的长.
31.如图,AC是四边形ABCD的对角线,,点E、F分别在AB、BC上,,,连接EF.
(1)求证:;
(2)若,,求的度数.
32.如图,在中(),,BC边上的中线AD把的周长分成60和40两部分,求AC和AB的长.
答案以及解析
1.答案:D
解析:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形,由此可知A,B,C不是三角形,D是三角形.故选D.
2.答案:D
解析:能够完全重合的两个图形叫做全等形.结合选项,知只有D项中的两个图形能够完全重合.故选D.
3.答案:B
解析:设第三边长为x,则由三角形三边关系得,即,故选B.
4.答案:B
解析:,,,,.,.故选B.
5.答案:A
解析:三角形三个内角的度数之比为,三个内角分别是,,.所以该三角形是锐角三角形.
6.答案:B
解析:,,,,,
,即.故B中结论正确,故选B.
7.答案:C
解析:AD是三角形ABC的高,,,,,,,故选C.
8.答案:D
解析:在△AOB和△DOC中,所以(SAS),所以,因为,所以圆形容器的壁厚为.故选D.
9.答案:A
解析:D是边BC的中点,的面积等于8,,E是边AB的中点,,故选A.
10.答案:C
解析:第①块仅保留了原三角形的一个角和部分边,不符合任何一种判定两个三角形全等的条件;第②块仅保留了原三角形的部分边,所以不符合任何一种判定两个三角形全等的条件;第③块不但保留了原三角形的两个角,还保留了其中一条边,所以符合用ASA判定两个三角形全等的条件,所以应该拿③去.故选C.
11.答案:B
解析:AD平分,.在和中,,,,,的周长为.故选B.
12.答案:D
解析:如图所示,.三个三角形是全等的,
.又,,的度数是180°.故选D.
1.3答案:4
解析:根据题意,得,即,又的长是偶数,所以.
14.答案:72°
解析:与是一组全等三角形,且,与是对应角,,,故答案为72°.
15答案:105°
解析:由三角形内角和定理,得.
16.答案:35°
解析:∵是的中点,∴.在和中,,∴,∴.
17.答案:
解析:应添加,在和中,,.
18.答案:1
解析:AD是的中线,,E是AD的中点,.
19.答案:2
解析:如图.,,,又AD是BC边上的高,,的面积.
20.答案:4
解析:如图,可以作出这样的三角形4个.
21.答案:20°
解析:,.,,,.
22.答案:②
解析:若添加①,则可由“AAS”判定;若添加②,则不能判定;若添加③,则可由“SAS”判定.
23.答案:(或或或)
解析:因为,所以.因为,所以.当添加或时,可根据“AAS”判定;当添加或时,可根据“ASA"判定.
24.答案:①③④
解析:,,即,又,要判定,需添加的条件为①;③;④.故填①③④.
25.答案:对应顶点:A和G,E和F,D和J,C和I,B和H;
对应边:AB和GH,AE和GF,ED和FJ,DC和JI,BC和HI;
对应角:和,和,和,和,和.
两个五边形全等,
,,,,.
26.答案:证明:,,即.
在和中,,
.
27.答案:(1)河宽AB是5米.
(2)由题意知,在和中,,
,.
故河宽AB就是测得的DE的长,因此他们的做法是正确的.
28.答案:AD是BC边上的高,,
,
,
,
AE是的平分线,
,
.
29.答案:若腰长为8cm,则底边长为(cm),此时,不能构成三角形,即这个等腰三角形的腰长不能为8cm.
若底边长为8cm,则腰长为(cm),
此时能构成三角形,所以这个等腰三角形的底边长为8cm,两腰长都是14cm,
即另外两边的长都是14cm.
综上可知,该等腰三角形的另外两边的长都为14cm.
30.答案:(1),.
,
,
.
(2),,
,即.
cm,cm,
(cm),
cm.
31.答案:(1)证明:在和中,
,
,
.
(2),,
,
,
.
32.答案:AD是BC边上的中线,,
设,,则,
,.
分为两种情况:
①,,则,,
解得,,即,;
②,,则,,
解得,,即,,,
由于,故不符合三角形的三边关系.
综上所述,,.
