沪教版(上海)高二数学上册 雪花曲线的初步研究 课件(共16张PPT)
文档属性
| 名称 | 沪教版(上海)高二数学上册 雪花曲线的初步研究 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
雪花曲线的初步研究
探究与实践
01
雪花曲线的制作
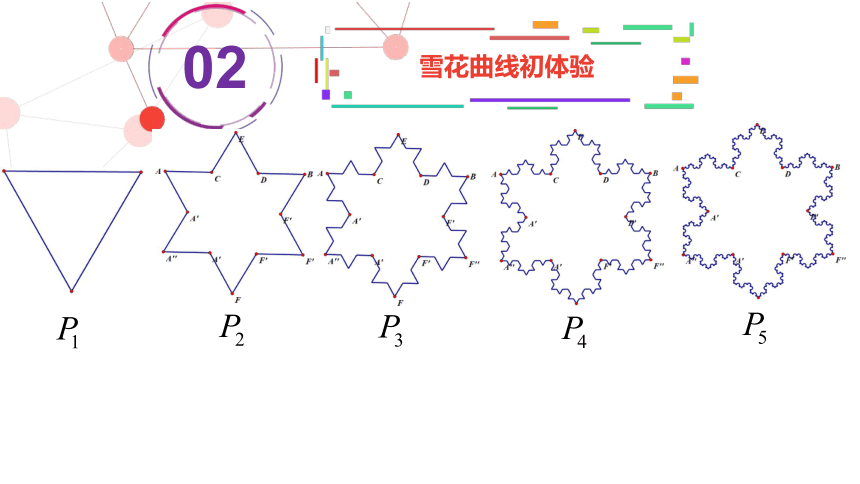
给出一个正三角形(记为P1),然后把三角形的每一条边三等分,以居中的一条线段为边向外作正三角形,并把居中的线段去掉(记为P2)
。
在P2的基础上,重复第一步的操作,生成新对象P3
再按上述方法无限次继续下去,所得到的曲线称为
科克雪花曲线(koch
snowflake)
02
雪花曲线初体验
03
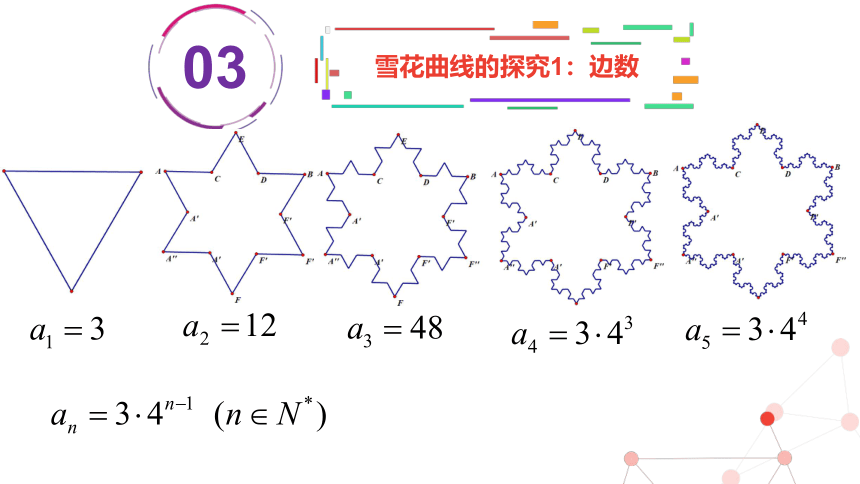
雪花曲线的探究1:边数
03
雪花曲线的探究2:边长
03
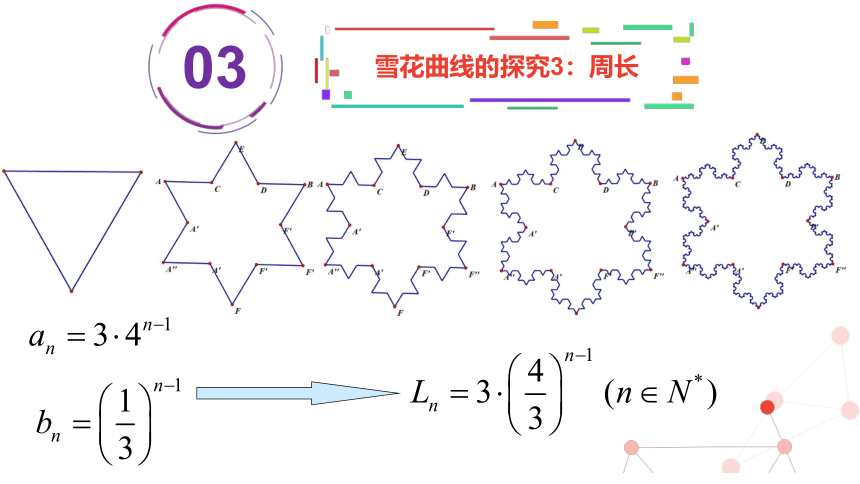
雪花曲线的探究3:周长
03
雪花曲线的探究4:面积
03
雪花曲线的探究4:面积
03
雪花曲线的探究5:性质
1.雪花曲线是一条边数无穷多,到处是尖端,不光滑的、连续封闭曲线。
2.雪花曲线的周长是无穷大,而它所围成的面积是有限的。
研究结论:
04
雪花曲线的探究拓展
把对象的细微部分放大后,其结构看起来仍与原先的一样,即图形的每一部分都和它本身的形状相似,这一相似特性叫做自相似性。
部分与整体存在自相似性的形状叫做分形
05
雪花曲线的探究变式
给出一个正三角形(记为P1),然后把三角形的每一条边三等分,以居中的一条线段为边向内作正三角形,并把居中的线段去掉(记为P2)
。
在P2的基础上,重复第一步的操作,生成新对象P3
再按上述方法无限次继续下去,所得到的曲线称为
反雪花曲线
05
反雪花曲线的探究
我们可以对反雪花曲线的哪些问题展开研究?
小 结
探究方法
研究流程
雪花曲线
周长无限
面积有限
数列基础知识
解决实际问题
分析资料
提出问题
解决问题
06
课后思考问题1
1.本节课我们看到确实存在着“边长”无限增大而面积有极限的图形,那么是否存在面积无限增大而周长是有极限的图形呢?
2.对雪花曲线的研究变式中,更改了等边三角形的方向,得到了反雪花曲线,同学们还能从其它角度对雪花曲线进行变式研究创造出属于自己的独一无二的雪花吗?(参考材料雪花曲线的变式小视频)
06
课后思考问题2
波兰著名的数学家谢尔宾斯基构造了几个典型的例子,常被称为“谢尔宾斯基三角形”
“谢尔宾斯基地毯”
“谢尔宾斯基海绵”
“谢尔宾斯基墓垛”,请大家查找资料,了解这些图形,并选择其中一个进行研究、探索。
Thanks
for
watching
雪花曲线的初步研究
探究与实践
01
雪花曲线的制作
给出一个正三角形(记为P1),然后把三角形的每一条边三等分,以居中的一条线段为边向外作正三角形,并把居中的线段去掉(记为P2)
。
在P2的基础上,重复第一步的操作,生成新对象P3
再按上述方法无限次继续下去,所得到的曲线称为
科克雪花曲线(koch
snowflake)
02
雪花曲线初体验
03
雪花曲线的探究1:边数
03
雪花曲线的探究2:边长
03
雪花曲线的探究3:周长
03
雪花曲线的探究4:面积
03
雪花曲线的探究4:面积
03
雪花曲线的探究5:性质
1.雪花曲线是一条边数无穷多,到处是尖端,不光滑的、连续封闭曲线。
2.雪花曲线的周长是无穷大,而它所围成的面积是有限的。
研究结论:
04
雪花曲线的探究拓展
把对象的细微部分放大后,其结构看起来仍与原先的一样,即图形的每一部分都和它本身的形状相似,这一相似特性叫做自相似性。
部分与整体存在自相似性的形状叫做分形
05
雪花曲线的探究变式
给出一个正三角形(记为P1),然后把三角形的每一条边三等分,以居中的一条线段为边向内作正三角形,并把居中的线段去掉(记为P2)
。
在P2的基础上,重复第一步的操作,生成新对象P3
再按上述方法无限次继续下去,所得到的曲线称为
反雪花曲线
05
反雪花曲线的探究
我们可以对反雪花曲线的哪些问题展开研究?
小 结
探究方法
研究流程
雪花曲线
周长无限
面积有限
数列基础知识
解决实际问题
分析资料
提出问题
解决问题
06
课后思考问题1
1.本节课我们看到确实存在着“边长”无限增大而面积有极限的图形,那么是否存在面积无限增大而周长是有极限的图形呢?
2.对雪花曲线的研究变式中,更改了等边三角形的方向,得到了反雪花曲线,同学们还能从其它角度对雪花曲线进行变式研究创造出属于自己的独一无二的雪花吗?(参考材料雪花曲线的变式小视频)
06
课后思考问题2
波兰著名的数学家谢尔宾斯基构造了几个典型的例子,常被称为“谢尔宾斯基三角形”
“谢尔宾斯基地毯”
“谢尔宾斯基海绵”
“谢尔宾斯基墓垛”,请大家查找资料,了解这些图形,并选择其中一个进行研究、探索。
Thanks
for
watching
