沪教版(上海)高二数学上册 10.1 算法的概念_4 课件(共25张PPT)
文档属性
| 名称 | 沪教版(上海)高二数学上册 10.1 算法的概念_4 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 11:48:20 | ||
图片预览







文档简介
(共25张PPT)
普通高中课程标准数学3(必修)
书
山
有
路
勤
为
径,学
海
无
崖
苦
作
舟
少
小
不
学
习,老
来
徒
伤
悲
成功=艰苦的劳动+正确的方法+少谈空话
天才就是百分之一的灵感,百分之九十九的汗水!
天
才
在
于
勤
奋,努
力
才
能
成
功!
勤劳的孩子展望未来,
但懒惰的孩子享受现在!!!
什
么
也
不
问
的
人
什
么
也
学
不
到
!!!
怀
天
下
,
求
真
知
,
学
做
人
算法的概念
算法初步
一、复习引入
算法作为一个名词,在中学教科书中并没有出现过,我们在基础教育阶段还没有接触算法概念。但是我们却从小学就开始接触算法,熟悉许多问题的算法。如,做四则运算要先乘除后加减,从里往外脱括弧,竖式笔算等都是算法,至于乘法口诀、珠算口诀更是算法的具体体现。广义地说,算法就是做某一件事的步骤或程序。菜谱是做菜肴的算法,洗衣机的使用说明书是操作洗衣机的算法,歌谱是一首歌曲的算法。在数学中,主要研究计算机能实现的算法,即按照某种机械程序步骤一定可以得到结果的解决问题的程序。(古代的计算工具:算筹与算盘.
20世纪最伟大的发明:计算机,计算机是强大的实现各种算法的工具。)
一、复习引入
要把大象装冰箱,分几步?哈哈
问:
2、现有九枚硬币,有一枚略重,你能用天平(不用砝码)将其找出来吗?设计一种最有效的方法,解决这一问题。
S1:把九枚硬币平均分成三份,取其中两份放天平上称,若平衡则重的在剩下的一份里,若不平衡则在重的一份里;
S2:在重的一份里取两枚放天平的两边,若平衡则剩下的一枚就是所找的,若不平衡则重的那枚就是所要找的。
二、提出问题
二、提出问题
3.一个农夫带着一只狼、一头山羊和一篮蔬菜要过河,但只有一条小船。乘船时,农夫只能带一样东西。当农夫在场的时候,这三样东西相安无事,一旦农夫不在,狼会吃羊,羊会吃菜。请设计一个方案,使农夫能安全地将这三样东西带过河。
S1:农夫带羊过河;
S2:农夫独自回来;
S3:农夫带狼过河;
S4:农夫带羊回来;
S5:农夫带蔬菜过河;
S6:农夫独自回来;
S7:农夫带羊过河。
算法通常指可以用来解决的某一类问题的步骤或程序,这些步骤或程序必须是明确的和有效的,而且能够在有限步之内完成的。
三、概念形成
概念1.算法(algorithm)
一般来说,“用算法解决问题”
可以利用计算机帮助完成。
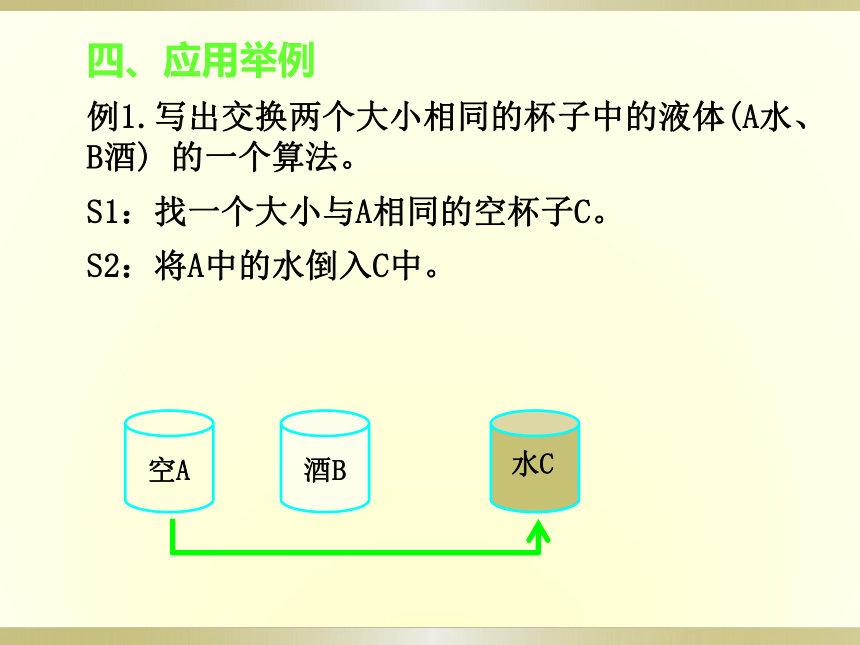
四、应用举例
例1.写出交换两个大小相同的杯子中的液体(A水、
B酒)
的一个算法。
S1:找一个大小与A相同的空杯子C。
酒B
空C
水A
四、应用举例
例1.写出交换两个大小相同的杯子中的液体(A水、
B酒)
的一个算法。
S1:找一个大小与A相同的空杯子C。
S2:将A中的水倒入C中。
酒B
水C
空A
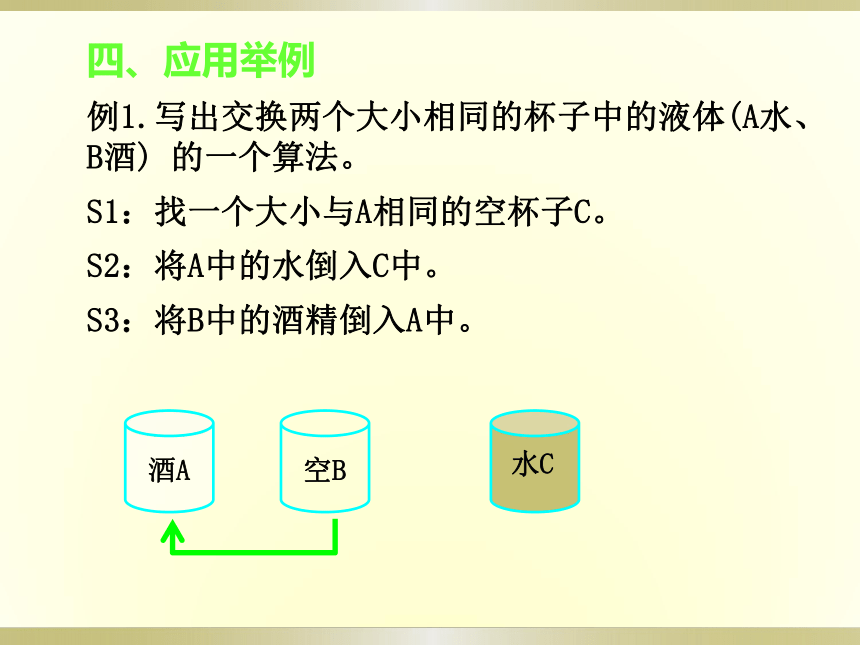
四、应用举例
例1.写出交换两个大小相同的杯子中的液体(A水、
B酒)
的一个算法。
S1:找一个大小与A相同的空杯子C。
S2:将A中的水倒入C中。
S3:将B中的酒精倒入A中。
空B
水C
酒A
四、应用举例
例1.写出交换两个大小相同的杯子中的液体(A水、
B酒)
的一个算法。
S1:找一个大小与A相同的空杯子C。
S4:将C中的水倒入B中,结束。
S2:将A中的水倒入C中。
S3:将B中的酒精倒入A中。
水B
空C
酒A
四、应用举例
例2.写出求一元二次方程ax2+bx+c=0的根的算法.
S1:计算Δ=b2-4ac.
S2:判断,如果Δ<0,则原方程无实数解;否则(Δ≥0)时,
S3:输出x1,
x2或无实数解的信息.
例3.解二元一次方程组
分析:解二元一次方程组的主要思想是消元的思想,有代入消元和加减消元两种消元的方法,下面用加减消元法写出它的求解过程
解:S1:②
-
①×2,得:
5y=3;
③
S2:解③得
S3:将
代入①,得
S4:结论:
本题的算法是由加减消元法求解的,这个算法也适合一般的二元一次方程组的解法。
四、应用举例
加减消元法解二元一次方程组的算法(利用计算机)
S2:解
得
③
S3:将
代入①,
得
S1:
得
②
-
①
③
四、应用举例
四、应用举例
例4.(1)设计一个算法判断7是否为质数。
S1:用2除7,得到余数1。因为余数不为0,所以2不能整除7。
S2:用3除7,得到余数1。因为余数不为0,所以3不能整除7。
S3:用4除7,得到余数3。因为余数不为0,所以4不能整除7。
S4:用5除7,得到余数2。因为余数不为0,所以5不能整除7。
S5:用6除7,得到余数1。因为余数不为0,所以6不能整除7。因此,7是质数。
四、应用举例
例4.(2)设计一个算法判断35是否为质数。
S1:用2除35,得到余数1。因为余数不为0,所以2不能整除35。
S2:用3除35,得到余数2。因为余数不为0,所以3不能整除35。
S3:用4除35,得到余数3。因为余数不为0,所以4不能整除7。
S4:用5除35,得到余数0。因为余数为0,所以5能整除35。因此,35不是质数。
四、应用举例
例4.(3)设计一个算法判断整数n(n>2)是否为质数。
S1:给定大于2的整数n。
S2:令i=2。
S3:用i除n,得余数r。
S4:判断“r=0”是否成立,若成立,则n不是质数,结束算法;否则,将i+1后返回第三步。
四、应用举例
在数学中,现代意义上的
“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.
2.算法的要求:
(1)写出的算法,必须能解决一类问题(例如解任意一个二元一次方程组),并且能重复使用;
(2)算法过程要能一步一步执行,每一步执行的操作,必须确切,不能含混不清,而且在有限步之内完成后能得出结果。
1.算法定义的理解:
四、应用举例
3.算法的基本特征:
明确性:算法对每一个步骤都有确切的,能有效执行且得到确定结果的,不能模棱两可。
顺序与正确性:算法从初始步骤开始,分为若干明确的步骤,每一步都只能有一个确定的继任者,只有执行完前一步才能进入到后一步,并且每一步都确定无误后,才能解决问题。
有限性:算法应由有限步组成,至少对某些输入,算法应在有限多步内结束,并给出计算结果。
不唯一性:求解某一个问题的解法不一定是唯一的,对于同一个问题可以有不同的解法。
四、应用举例
算法2:
S1:取n=100;
S3:输出运算结果。
S2:计算
点评:算法1繁琐,步骤较多;算法2简单,步骤较少。找出好的算法是我们的追求目标。
例5、给出求1+2+3+……+99+100的一个算法。
算法1:
S2:使S=1,i=2;
S3:使S的值变为S+i,i的值增加1;
S4:若i>100,则输出S,否则转到S3;
S1:给出两变量S,i;
四、应用举例
例6.用二分法设计一个求方程
的近似正根的算法,精确度0.005。
算法分析:回顾二分法解方程的过程,假设所求近似根与精确解的差的绝对值不超过0.005,则不难设计出以下步骤:
S1:令f(x)=x2-2,因为f(1)<0,f(2)>0,所以设a=1,b=2。
S2:令m=
,
判断f(m)是否为0。若是0,则m为所求;若否,则继续判断f(a)·f(m)大于0还是小于0
。
S3:若f(a)·f(m)
>0,则令a=m;否则,令b=m
。
S4:判断
|a-b|<0.005是否成立?若是,则a或b(或任意值)为满足条件的近似根;若否,则返回S2。
评析:实际上,上述步骤就是在求
的近似值。
例7.现有有限个实数,怎样从中找出最大值?
S1:先假定这些实数中的第一个数为“最大值”。
S2:将这些实数中的下一个数与“最大值”比较,如果它大于此“最大值”,这时就假定“最大值”是这个实数。
S3:如果还有其他实数,重复S2。
S4:一直到没有可比的数为止,这时假定的“最大值”就是这有限个实数的最大值。
四、应用举例
例8.应用Scilab计算指令解方程组:(体会计算机的应用)
四、应用举例
五、课堂练习
思考
?
课本第7页,练习A,1,2,3,4
2.算法的特点:思路简单清晰,叙述复杂,步骤繁琐,计算量大,完全依靠人力难以完成。而这些恰恰就是计算机的特长,它能不厌其烦地完成枯燥的、重复的繁琐的工作。正因为这些,现代算法的作用之一就是使计算机代替人完成某些工作,这也是我们学习算法的重要原因之一。
六、课堂总结
1.知识结构
算法的概念
算法的步骤
算法的特点
算法
六、课堂总结
3.设计算法的注意事项:
(1)认真分析问题,联系解决此问题的一般数学方法;
(2)综合考虑此类问题中可能涉及的各种情况;
(3)借助有关的变量或参数对算法加以表达;
(4)将解决问题的过程划分为若干个步骤;
(5)然后用简练的语言将各个步骤表示出来。
普通高中课程标准数学3(必修)
书
山
有
路
勤
为
径,学
海
无
崖
苦
作
舟
少
小
不
学
习,老
来
徒
伤
悲
成功=艰苦的劳动+正确的方法+少谈空话
天才就是百分之一的灵感,百分之九十九的汗水!
天
才
在
于
勤
奋,努
力
才
能
成
功!
勤劳的孩子展望未来,
但懒惰的孩子享受现在!!!
什
么
也
不
问
的
人
什
么
也
学
不
到
!!!
怀
天
下
,
求
真
知
,
学
做
人
算法的概念
算法初步
一、复习引入
算法作为一个名词,在中学教科书中并没有出现过,我们在基础教育阶段还没有接触算法概念。但是我们却从小学就开始接触算法,熟悉许多问题的算法。如,做四则运算要先乘除后加减,从里往外脱括弧,竖式笔算等都是算法,至于乘法口诀、珠算口诀更是算法的具体体现。广义地说,算法就是做某一件事的步骤或程序。菜谱是做菜肴的算法,洗衣机的使用说明书是操作洗衣机的算法,歌谱是一首歌曲的算法。在数学中,主要研究计算机能实现的算法,即按照某种机械程序步骤一定可以得到结果的解决问题的程序。(古代的计算工具:算筹与算盘.
20世纪最伟大的发明:计算机,计算机是强大的实现各种算法的工具。)
一、复习引入
要把大象装冰箱,分几步?哈哈
问:
2、现有九枚硬币,有一枚略重,你能用天平(不用砝码)将其找出来吗?设计一种最有效的方法,解决这一问题。
S1:把九枚硬币平均分成三份,取其中两份放天平上称,若平衡则重的在剩下的一份里,若不平衡则在重的一份里;
S2:在重的一份里取两枚放天平的两边,若平衡则剩下的一枚就是所找的,若不平衡则重的那枚就是所要找的。
二、提出问题
二、提出问题
3.一个农夫带着一只狼、一头山羊和一篮蔬菜要过河,但只有一条小船。乘船时,农夫只能带一样东西。当农夫在场的时候,这三样东西相安无事,一旦农夫不在,狼会吃羊,羊会吃菜。请设计一个方案,使农夫能安全地将这三样东西带过河。
S1:农夫带羊过河;
S2:农夫独自回来;
S3:农夫带狼过河;
S4:农夫带羊回来;
S5:农夫带蔬菜过河;
S6:农夫独自回来;
S7:农夫带羊过河。
算法通常指可以用来解决的某一类问题的步骤或程序,这些步骤或程序必须是明确的和有效的,而且能够在有限步之内完成的。
三、概念形成
概念1.算法(algorithm)
一般来说,“用算法解决问题”
可以利用计算机帮助完成。
四、应用举例
例1.写出交换两个大小相同的杯子中的液体(A水、
B酒)
的一个算法。
S1:找一个大小与A相同的空杯子C。
酒B
空C
水A
四、应用举例
例1.写出交换两个大小相同的杯子中的液体(A水、
B酒)
的一个算法。
S1:找一个大小与A相同的空杯子C。
S2:将A中的水倒入C中。
酒B
水C
空A
四、应用举例
例1.写出交换两个大小相同的杯子中的液体(A水、
B酒)
的一个算法。
S1:找一个大小与A相同的空杯子C。
S2:将A中的水倒入C中。
S3:将B中的酒精倒入A中。
空B
水C
酒A
四、应用举例
例1.写出交换两个大小相同的杯子中的液体(A水、
B酒)
的一个算法。
S1:找一个大小与A相同的空杯子C。
S4:将C中的水倒入B中,结束。
S2:将A中的水倒入C中。
S3:将B中的酒精倒入A中。
水B
空C
酒A
四、应用举例
例2.写出求一元二次方程ax2+bx+c=0的根的算法.
S1:计算Δ=b2-4ac.
S2:判断,如果Δ<0,则原方程无实数解;否则(Δ≥0)时,
S3:输出x1,
x2或无实数解的信息.
例3.解二元一次方程组
分析:解二元一次方程组的主要思想是消元的思想,有代入消元和加减消元两种消元的方法,下面用加减消元法写出它的求解过程
解:S1:②
-
①×2,得:
5y=3;
③
S2:解③得
S3:将
代入①,得
S4:结论:
本题的算法是由加减消元法求解的,这个算法也适合一般的二元一次方程组的解法。
四、应用举例
加减消元法解二元一次方程组的算法(利用计算机)
S2:解
得
③
S3:将
代入①,
得
S1:
得
②
-
①
③
四、应用举例
四、应用举例
例4.(1)设计一个算法判断7是否为质数。
S1:用2除7,得到余数1。因为余数不为0,所以2不能整除7。
S2:用3除7,得到余数1。因为余数不为0,所以3不能整除7。
S3:用4除7,得到余数3。因为余数不为0,所以4不能整除7。
S4:用5除7,得到余数2。因为余数不为0,所以5不能整除7。
S5:用6除7,得到余数1。因为余数不为0,所以6不能整除7。因此,7是质数。
四、应用举例
例4.(2)设计一个算法判断35是否为质数。
S1:用2除35,得到余数1。因为余数不为0,所以2不能整除35。
S2:用3除35,得到余数2。因为余数不为0,所以3不能整除35。
S3:用4除35,得到余数3。因为余数不为0,所以4不能整除7。
S4:用5除35,得到余数0。因为余数为0,所以5能整除35。因此,35不是质数。
四、应用举例
例4.(3)设计一个算法判断整数n(n>2)是否为质数。
S1:给定大于2的整数n。
S2:令i=2。
S3:用i除n,得余数r。
S4:判断“r=0”是否成立,若成立,则n不是质数,结束算法;否则,将i+1后返回第三步。
四、应用举例
在数学中,现代意义上的
“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.
2.算法的要求:
(1)写出的算法,必须能解决一类问题(例如解任意一个二元一次方程组),并且能重复使用;
(2)算法过程要能一步一步执行,每一步执行的操作,必须确切,不能含混不清,而且在有限步之内完成后能得出结果。
1.算法定义的理解:
四、应用举例
3.算法的基本特征:
明确性:算法对每一个步骤都有确切的,能有效执行且得到确定结果的,不能模棱两可。
顺序与正确性:算法从初始步骤开始,分为若干明确的步骤,每一步都只能有一个确定的继任者,只有执行完前一步才能进入到后一步,并且每一步都确定无误后,才能解决问题。
有限性:算法应由有限步组成,至少对某些输入,算法应在有限多步内结束,并给出计算结果。
不唯一性:求解某一个问题的解法不一定是唯一的,对于同一个问题可以有不同的解法。
四、应用举例
算法2:
S1:取n=100;
S3:输出运算结果。
S2:计算
点评:算法1繁琐,步骤较多;算法2简单,步骤较少。找出好的算法是我们的追求目标。
例5、给出求1+2+3+……+99+100的一个算法。
算法1:
S2:使S=1,i=2;
S3:使S的值变为S+i,i的值增加1;
S4:若i>100,则输出S,否则转到S3;
S1:给出两变量S,i;
四、应用举例
例6.用二分法设计一个求方程
的近似正根的算法,精确度0.005。
算法分析:回顾二分法解方程的过程,假设所求近似根与精确解的差的绝对值不超过0.005,则不难设计出以下步骤:
S1:令f(x)=x2-2,因为f(1)<0,f(2)>0,所以设a=1,b=2。
S2:令m=
,
判断f(m)是否为0。若是0,则m为所求;若否,则继续判断f(a)·f(m)大于0还是小于0
。
S3:若f(a)·f(m)
>0,则令a=m;否则,令b=m
。
S4:判断
|a-b|<0.005是否成立?若是,则a或b(或任意值)为满足条件的近似根;若否,则返回S2。
评析:实际上,上述步骤就是在求
的近似值。
例7.现有有限个实数,怎样从中找出最大值?
S1:先假定这些实数中的第一个数为“最大值”。
S2:将这些实数中的下一个数与“最大值”比较,如果它大于此“最大值”,这时就假定“最大值”是这个实数。
S3:如果还有其他实数,重复S2。
S4:一直到没有可比的数为止,这时假定的“最大值”就是这有限个实数的最大值。
四、应用举例
例8.应用Scilab计算指令解方程组:(体会计算机的应用)
四、应用举例
五、课堂练习
思考
?
课本第7页,练习A,1,2,3,4
2.算法的特点:思路简单清晰,叙述复杂,步骤繁琐,计算量大,完全依靠人力难以完成。而这些恰恰就是计算机的特长,它能不厌其烦地完成枯燥的、重复的繁琐的工作。正因为这些,现代算法的作用之一就是使计算机代替人完成某些工作,这也是我们学习算法的重要原因之一。
六、课堂总结
1.知识结构
算法的概念
算法的步骤
算法的特点
算法
六、课堂总结
3.设计算法的注意事项:
(1)认真分析问题,联系解决此问题的一般数学方法;
(2)综合考虑此类问题中可能涉及的各种情况;
(3)借助有关的变量或参数对算法加以表达;
(4)将解决问题的过程划分为若干个步骤;
(5)然后用简练的语言将各个步骤表示出来。
