沪教版(上海)高二数学上册 9.2 矩阵的运算_ 课件(共19张PPT)
文档属性
| 名称 | 沪教版(上海)高二数学上册 9.2 矩阵的运算_ 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 836.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 00:00:00 | ||
图片预览




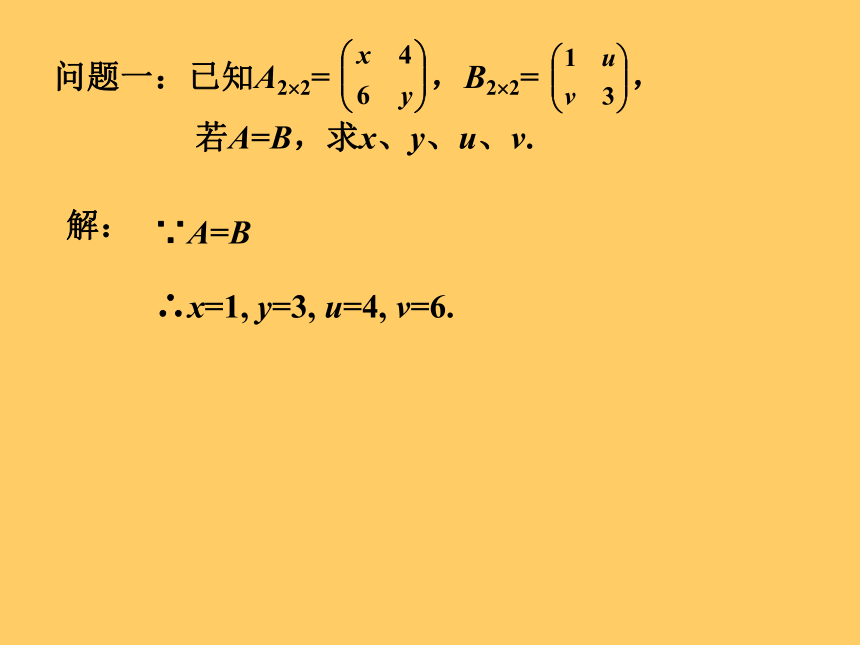

文档简介
(共19张PPT)
矩阵的运算
为了公平合理真实地反映学生在校学习情况,将平时成绩的30%,期中考试的30%,期末考试的40%相加生成学期总评记入学生学习档案。有甲、乙、丙三位同学的语文、数学、英语三门功课的期中、期末成绩如下表所示:
语文
数学
英语
平时
期中
期末
平时
期中
期末
平时
期中
期末
甲
80
70
75
90
80
85
70
80
75
乙
90
70
80
80
80
75
80
90
85
丙
60
80
70
80
90
95
90
80
85
(1)如何用矩阵表示三位同学各科在平时、
期中、期末的成绩?
(2)如何得到这三位同学在平时、期中、期末时,
语文、数学、英语三门课的总成绩?
(3)如何得到这三位同学在期中、期末各科成绩
的增幅?
(4)如何求三位同学的总评成绩?
若矩阵A和矩阵B的行数与列数分别相等,则A和B叫做同阶矩阵。
若A=(aij)和B=(bij)是同阶矩阵,且矩阵A中每一个元素与矩阵B中相同位置的元素都相等,即aij=bij,则称两矩阵相等,记做A=B。
我们把m行n列矩阵的第i行第j列元素用圆括号括起来表示矩阵,记为A=(aij)
1.
可用A=(aij)表示矩阵
2.
同阶矩阵
3.
矩阵的相等
问题一:已知A2?2=
,B2?2=
,
若A=B,求x、y、u、v.
解:
∴x=1,
y=3,
u=4,
v=6.
∵A=B
1.
矩阵的和与差
记作:A+B
上述运算叫做矩阵的加法(减法).
(相减cij=aij?bij)
当两个矩阵A,B的行数和列数分别相等时,
将它们对应位置上的元素相加
i=1,2,…,m;j=1,2,…,n
cij=aij+bij
所得到的矩阵cij称为矩阵A,B的和
(差),
(A-B)
语文
数学
英语
平时
期中
期末
平时
期中
期末
平时
期中
期末
甲
80
70
75
90
80
85
70
80
75
乙
90
70
80
80
80
75
80
90
85
丙
60
80
70
80
90
95
90
80
85
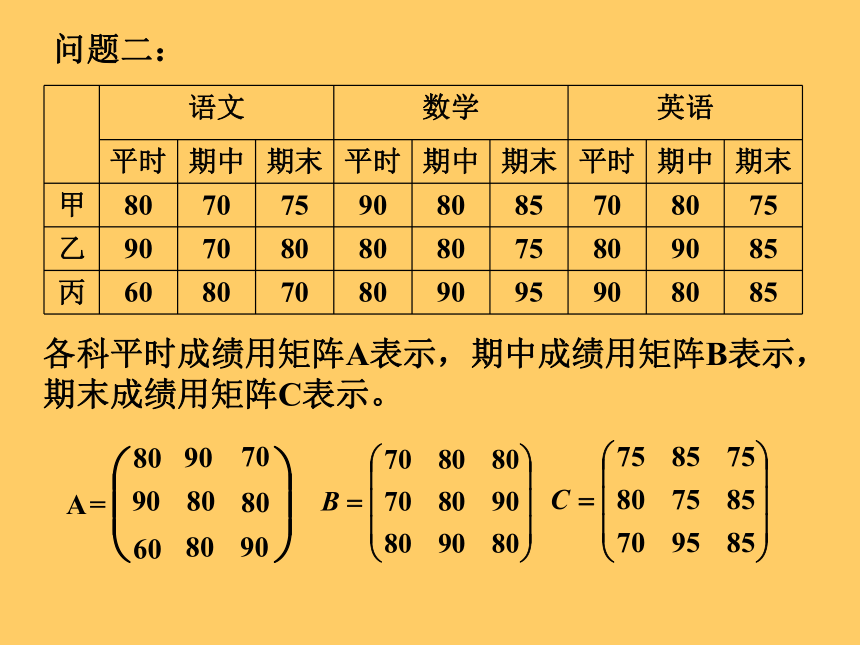
各科平时成绩用矩阵A表示,期中成绩用矩阵B表示,
期末成绩用矩阵C表示。
A
=
80
90
70
90
80
80
60
80
90
问题二:
平时、期中、期末总成绩用矩阵D表示,期中、期末成绩的增幅用矩阵E表示,求矩阵D和E。
D
=
225
255
225
240
235
255
210
265
255
E
=
5
5
-5
10
-5
-5
-10
5
5
甲同学在期末考试中,
语文和数学成绩都有提高,
英语成绩有所下降。
A+B+C
=
C?B
=
3.
由实数的加法有交换律和结合律,
可类比得到同阶矩阵的加法满足:
A+B=B+A
加法的交换律
(A+B)+C=A+(B+C)
加法的结合律
1.
只有同阶矩阵的加、减才有意义;
两同阶矩阵的加、减是它们对应位置的元素
相加减;
设k为任意实数,把矩阵A的所有元素与k相乘
得到的矩阵叫做矩阵A与实数k的乘积矩阵.
记作:kA
(kA=(kaij))
2.
数与矩阵的积
问题三:(1)计算甲、乙、丙三位同学平时、期中、
期末各科平均成绩对应的矩阵F。
D
=
225
255
225
240
235
255
210
265
255
A+B+C
=
=
=
A
=
80
90
70
90
80
80
60
80
90
F=
(2)求三位同学的学期总评对应的矩阵G
A
=
80
90
70
90
80
80
60
80
90
由平时成绩的30%,期中考试的30%,期末考试的40%
相加生成学期总评成绩。
=
0.3?80+0.3?70+0.4?75
75
90?0.3+80?0.3+85?0.4
85
75
78
75
70
89
85
G=
数与矩阵的乘法满足:
1.
分配律
k(A+B)=kA+kB
(k+l)A=kA+lA
结合律
(kl)A=k(lA)=l(kA)
2.
移项法则
A+B=C?A=C?B或B=C?A
加法与减法的互化
A?B=A+(?1)B
(1)将二元一次方程组
用矩阵的
运算来表示;
(2)讨论方程组存在唯一解的条件。
解:(1)原方程组可以表示为:
(2)当向量
与
不平行时,
问题4:已知二元一次方程组
由平面向量分解定理知,存在唯一实数
x,y,使
,即
方程组有唯一解。
当向量
与
平行时,
对任意的x,y,
都与
或
平行,
,则方程组有无穷多解;
,则方程组无解。
已知
,
,
且A+2X=B,求X。
解:
由A+2X=B
?
X=
=
2.
两个同为m行n列的矩阵加减运算,
是其对应位置的元素相加减。
3.
数与矩阵相乘,是数与其每个元素相乘。
4.
由矩阵的加减法、数乘的定义决定了实数
加减法和乘法的运算律仍适合于矩阵。
两个同阶矩阵对应位置上的元素相同,
则说这两个矩阵相等。
1、思考题:统计你家今年第二季度水、电、煤气使用情况:
月份
用水(m3)
排水(m3)
电(千瓦时)
煤气(m3)
4月
5月
6月
单价(元)
1.03
0.90
0.61
1.05
用矩阵运算求:
(1)按月计算去第二季度4、5、6月份水、电、煤气的开支费用;
(2)分别计算第二季度水、电、煤气的开支费用;
(3)计算第二季度水、电、煤气总开支费用。
2、选做题:已知4A+2B=
,
A?B=
,
(1)求A和B;(2)求7A+5B.
矩阵的运算
为了公平合理真实地反映学生在校学习情况,将平时成绩的30%,期中考试的30%,期末考试的40%相加生成学期总评记入学生学习档案。有甲、乙、丙三位同学的语文、数学、英语三门功课的期中、期末成绩如下表所示:
语文
数学
英语
平时
期中
期末
平时
期中
期末
平时
期中
期末
甲
80
70
75
90
80
85
70
80
75
乙
90
70
80
80
80
75
80
90
85
丙
60
80
70
80
90
95
90
80
85
(1)如何用矩阵表示三位同学各科在平时、
期中、期末的成绩?
(2)如何得到这三位同学在平时、期中、期末时,
语文、数学、英语三门课的总成绩?
(3)如何得到这三位同学在期中、期末各科成绩
的增幅?
(4)如何求三位同学的总评成绩?
若矩阵A和矩阵B的行数与列数分别相等,则A和B叫做同阶矩阵。
若A=(aij)和B=(bij)是同阶矩阵,且矩阵A中每一个元素与矩阵B中相同位置的元素都相等,即aij=bij,则称两矩阵相等,记做A=B。
我们把m行n列矩阵的第i行第j列元素用圆括号括起来表示矩阵,记为A=(aij)
1.
可用A=(aij)表示矩阵
2.
同阶矩阵
3.
矩阵的相等
问题一:已知A2?2=
,B2?2=
,
若A=B,求x、y、u、v.
解:
∴x=1,
y=3,
u=4,
v=6.
∵A=B
1.
矩阵的和与差
记作:A+B
上述运算叫做矩阵的加法(减法).
(相减cij=aij?bij)
当两个矩阵A,B的行数和列数分别相等时,
将它们对应位置上的元素相加
i=1,2,…,m;j=1,2,…,n
cij=aij+bij
所得到的矩阵cij称为矩阵A,B的和
(差),
(A-B)
语文
数学
英语
平时
期中
期末
平时
期中
期末
平时
期中
期末
甲
80
70
75
90
80
85
70
80
75
乙
90
70
80
80
80
75
80
90
85
丙
60
80
70
80
90
95
90
80
85
各科平时成绩用矩阵A表示,期中成绩用矩阵B表示,
期末成绩用矩阵C表示。
A
=
80
90
70
90
80
80
60
80
90
问题二:
平时、期中、期末总成绩用矩阵D表示,期中、期末成绩的增幅用矩阵E表示,求矩阵D和E。
D
=
225
255
225
240
235
255
210
265
255
E
=
5
5
-5
10
-5
-5
-10
5
5
甲同学在期末考试中,
语文和数学成绩都有提高,
英语成绩有所下降。
A+B+C
=
C?B
=
3.
由实数的加法有交换律和结合律,
可类比得到同阶矩阵的加法满足:
A+B=B+A
加法的交换律
(A+B)+C=A+(B+C)
加法的结合律
1.
只有同阶矩阵的加、减才有意义;
两同阶矩阵的加、减是它们对应位置的元素
相加减;
设k为任意实数,把矩阵A的所有元素与k相乘
得到的矩阵叫做矩阵A与实数k的乘积矩阵.
记作:kA
(kA=(kaij))
2.
数与矩阵的积
问题三:(1)计算甲、乙、丙三位同学平时、期中、
期末各科平均成绩对应的矩阵F。
D
=
225
255
225
240
235
255
210
265
255
A+B+C
=
=
=
A
=
80
90
70
90
80
80
60
80
90
F=
(2)求三位同学的学期总评对应的矩阵G
A
=
80
90
70
90
80
80
60
80
90
由平时成绩的30%,期中考试的30%,期末考试的40%
相加生成学期总评成绩。
=
0.3?80+0.3?70+0.4?75
75
90?0.3+80?0.3+85?0.4
85
75
78
75
70
89
85
G=
数与矩阵的乘法满足:
1.
分配律
k(A+B)=kA+kB
(k+l)A=kA+lA
结合律
(kl)A=k(lA)=l(kA)
2.
移项法则
A+B=C?A=C?B或B=C?A
加法与减法的互化
A?B=A+(?1)B
(1)将二元一次方程组
用矩阵的
运算来表示;
(2)讨论方程组存在唯一解的条件。
解:(1)原方程组可以表示为:
(2)当向量
与
不平行时,
问题4:已知二元一次方程组
由平面向量分解定理知,存在唯一实数
x,y,使
,即
方程组有唯一解。
当向量
与
平行时,
对任意的x,y,
都与
或
平行,
,则方程组有无穷多解;
,则方程组无解。
已知
,
,
且A+2X=B,求X。
解:
由A+2X=B
?
X=
=
2.
两个同为m行n列的矩阵加减运算,
是其对应位置的元素相加减。
3.
数与矩阵相乘,是数与其每个元素相乘。
4.
由矩阵的加减法、数乘的定义决定了实数
加减法和乘法的运算律仍适合于矩阵。
两个同阶矩阵对应位置上的元素相同,
则说这两个矩阵相等。
1、思考题:统计你家今年第二季度水、电、煤气使用情况:
月份
用水(m3)
排水(m3)
电(千瓦时)
煤气(m3)
4月
5月
6月
单价(元)
1.03
0.90
0.61
1.05
用矩阵运算求:
(1)按月计算去第二季度4、5、6月份水、电、煤气的开支费用;
(2)分别计算第二季度水、电、煤气的开支费用;
(3)计算第二季度水、电、煤气总开支费用。
2、选做题:已知4A+2B=
,
A?B=
,
(1)求A和B;(2)求7A+5B.
