沪教版(上海)高二数学上册 第7章 数列与数学归纳法 复习 课件(共63张PPT)
文档属性
| 名称 | 沪教版(上海)高二数学上册 第7章 数列与数学归纳法 复习 课件(共63张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 00:00:00 | ||
图片预览











文档简介
(共63张PPT)
第7章
数列与数学归纳法
复习课件
题型探究
知识梳理
内容索引
当堂训练
知识梳理
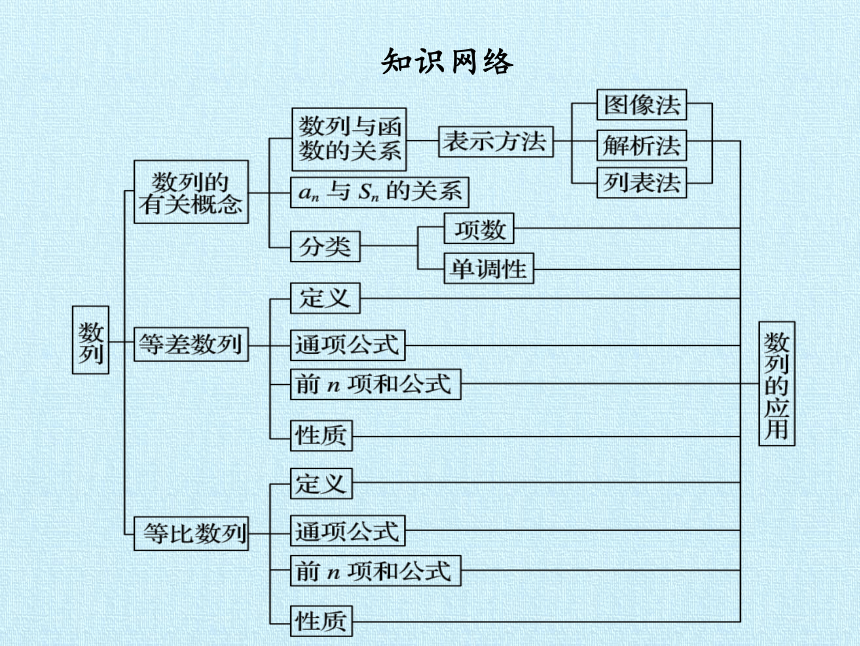
知识网络
对比归纳等差数列和等比数列的基本概念和公式
?
等差数列
等比数列
定义
如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫作等差数列,这个常数叫作等差数列的公差,公差通常用字母d表示
如果一个数列从第2项起,每一项与它的前一项的比等于同一常数,那么这个数列叫作等比数列,这个常数叫作等比数列的公比,公比通常用字母q表示(q≠0)
递推公式
an+1-an=d
=q
中项
由三个数a,A,b组成的等差数列可以看成最简单的等差数列。这时A叫作a与b的等差中项,并且A=
如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项,且G=
通项公式
an=a1+(n-1)d
an=a1qn-1
前n项和公式
q≠1时,Sn=
=
,q=1时,Sn=na1
性质
am,an的关系
am-an=(m-n)d
=qm-n
m,n,s,t∈N+,m+n=s+t
am+an=as+at
aman=asat
{kn}是等差数列,且kn∈N+
{
}是等差数列
{
}是等比数列
n=2k-1,k∈N+
S2k-1=(2k-1)·ak
a1a2·…·a2k-1=
判
断
方
法
利用定义
an+1-an是同一常数
是同一常数
利用中项
an+an+2=2an+1
anan+2=
利用通项公式
an=pn+q,其中p、q为常数
an=abn(a≠0,b≠0)
利用前n项和公式
Sn=an2+bn
(a,b为常数)
Sn=A(qn-1),其中A≠0,q≠0且q≠1或Sn=np(p为非零常数)
数学归纳法:对于某些与自然数n有关的命题常常采用下面的方法来证明它的正确性:
先证明当n取第一个值n0时命题成立;然后假设当n=k
(k?N
,k≥n0)时命题成立,证明当n=k+1时命题也成立这种证明方法就叫做数学归纳法
数学归纳法的基本思想:
即先验证使结论有意义的最小的正整数n0,如果当n=n0时,命题成立,再假设当n=k(k≥n0,k∈N
)时,命题成立(这时命题是否成立不是确定的)。根据这个假设,如能推出当n=k+1时,命题也成立,那么就可以递推出对所有不小于n0的正整数n0+1,n0+2,…,命题都成立。
数列极限的描述性定义
读作
“n
趋向于无穷大时,
的极限等于A
”
一般地,在n无限增大的变化过程中,如果
无穷数列
中的项
无限趋近于一个常数A,
那么A叫做数列
的极限,或叫做数列
收敛于A。
(即
无限趋近于0)
记作
(C
是常数)
常用的数列极限
数列极限的运算性质:
前提
无穷等比数列的各项和
首项为a1?0,
公比为?q??1的无穷等比数列的前n项和为Sn,
当n??时Sn的极限,
称为无穷等比数列的各项和。
并用符号S表示,
即:
对于一个m项的有穷数列{an}(n?1,2,……,m),
我们也可以定义其各项和,
即定义为:
对于有穷数列而言,
各项和总是存在的。
题型探究
类型一 方程思想求解数列问题
例1 设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和。已知S3=7,且a1+3,3a2,a3+4构成等差数列。
(1)求数列{an}的通项;
解答
故数列{an}的通项为an=2n-1。
(2)令bn=ln
a3n+1,n=1,2,…,求数列{bn}的前n项和Tn。
解答
由于bn=ln
a3n+1,n=1,2,…,
由(1)得a3n+1=23n,∴bn=ln
23n=3nln
2。
又bn+1-bn=3ln
2,∴{bn}是等差数列,
反思与感悟
在等差数列和等比数列中,通项公式an和前n项和公式Sn共涉及五个量:a1,an,n,q(d),Sn,其中首项a1和公比q(公差d)为基本量,“知三求二”是指将已知条件转换成关于a1,an,n,q(d),Sn的方程组,通过方程的思想解出需要的量。
跟踪训练1 记等差数列
的前n项和为Sn,设S3=12,且2a1,a2,a3
+1成等比数列,求Sn。
解答
类型二 转化与化归思想求解数列问题
例1 在数列{an}中,Sn+1=4an+2,a1=1。
(1)
设cn=
,求证数列{cn}是等差数列;
证明
由Sn+1=4an+2,
①
则当n≥2,n∈N+时,有Sn=4an-1+2
②
①-②得an+1=4an-4an-1
方法一 对an+1=4an-4an-1两边同除以2n+1,得
即cn+1+cn-1=2cn,
∴数列{cn}是等差数列。
由Sn+1=4an+2,得a1+a2=4a1+2,则a2=3a1+2=5,
方法二 ∵an+1-2an=2an-4an-1=2(an-2an-1),
令bn=an+1-2an
则{bn}是以a2-2a1=4a1+2-a1-2a1=3为首项,2为公比的等比数列,
∴bn=3·2n-1
(2)
求数列{an}的通项公式及前n项和的公式。
解答
设Sn=(3-1)·2-1+(3×2-1)·20+…+(3n-1)·2n-2,
∴2Sn=(3-1)·20+(3×2-1)·21+…+(3n-1)·2n-1,
故Sn=2Sn-Sn
=-(3-1)·2-1-3(20+21+…+2n-2)+(3n-1)·2n-1
=-1+3+(3n-4)·2n-1
=2+(3n-4)·2n-1
∴
数列{an}的通项公式为an=(3n-1)·2n-2,前n项和公式为Sn=2+(3n-4)·2n-1,n∈N+。
反思与感悟
由递推公式求通项公式,要求掌握的方法有两种,一种求法是先找出数列的前几项,通过观察、归纳得出,然后证明;另一种是通过变形转化为等差数列或等比数列,再用公式求出。
跟踪训练1 设数列{an}的前n项和为Sn,已知a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N+)。
(1)求a2,a3的值;
∵a1+2a2+3a3+…+nan
=(n-1)Sn+2n(n∈N+),
∴当n=1时,a1=2×1=2;
当n=2时,a1+2a2=(a1+a2)+4,∴a2=4;
当n=3时,a1+2a2+3a3=2(a1+a2+a3)+6,∴a3=8。
解答
(2)求证:数列{Sn+2}是等比数列。
证明
∵a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N
),
①
∴当n≥2时,a1+2a2+3a3+…+(n-1)an-1
=(n-2)Sn-1+2(n-1)。
②
①-②得nan=(n-1)Sn-(n-2)Sn-1+2
=n(Sn-Sn-1)-Sn+2Sn-1+2
=nan-Sn+2Sn-1+2。
∴-Sn+2Sn-1+2=0,即Sn=2Sn-1+2,
∴Sn+2=2(Sn-1+2)。
∵S1+2=4≠0,∴Sn-1+2≠0,
∴
=2,
故{Sn+2}是以4为首项,2为公比的等比数列。
类型三 函数思想求解数列问题
命题角度1 借助函数性质解数列问题
例1 已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别是一个等比数列的第2项、第3项、第4项。
(1)求数列{an}的通项公式;
解答
由题意得(a1+d)(a1+13d)=(a1+4d)2,
整理得2a1d=d2。∵d>0,∴d=2。
∵a1=1。∴an=2n-1
(n∈N+)。
(2)设bn=
(n∈N+),Sn=b1+b2+…+bn,是否存在t,使得对任意的n均有Sn>
总成立?若存在,求出最大的整数t;若不存在,请说明理由。
解答
∴数列{Sn}是递增的。
又∵t∈Z,∴适合条件的t的最大值为8。
反思与感悟
数列是一种特殊的函数,在求解数列问题时,若涉及参数取值范围,最值问题或单调性时,均可考虑采用函数的性质及研究方法指导解题。值得注意的是数列定义域是正整数集或{1,2,3,…,n},这一特殊性对问题结果可能造成影响。
跟踪训练1 已知首项为
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N+),且S3+a3,S5+a5,S4+a4成等差数列。
(1)求数列{an}的通项公式;
解答
设等比数列{an}的公比为q,
因为S3+a3,S5+a5,S4+a4成等差数列,
所以S5+a5-S3-a3=S4+a4-S5-a5,
(2)设Tn=Sn-
(n∈N+),求数列{Tn}最大项的值与最小项的值。
解答
命题角度2 以函数为载体给出数列
例2 已知函数f(x)=2-|x|,无穷数列{an}满足an+1=f(an),n∈N+。
(1)若a1=0,求a2,a3,a4;
解答
由an+1=f(an)?an+1=2-|an|,
a1=0?a2=2,a3=0,a4=2。
(2)若a1>0,且a1,a2,a3成等比数列,求a1的值。
解答
=a1[2-|2-|a1||]?(2-a1)2=a1[2-|2-a1|],
分情况讨论:
反思与感悟
以函数为载体给出数列,只需代入函数式即可转化为数列问题。
跟踪训练2 已知函数f(x)=
,数列{an}满足
a1=1,an+1=
,n∈N+。
(1)求数列{an}的通项公式;
解答
(2)令Tn=a1a2-a2a3+a3a4-a4a5+…-a2na2n+1,求Tn。
解答
Tn=a1a2-a2a3+a3a4-a4a5+…-a2na2n+1
=a2(a1-a3)+a4(a3-a5)+…+a2n(a2n-1-a2n+1)
类型四 数学归纳法
例1
用数学归纳法证明:如果{an}是一个等差数列,公差是d,那么an=a1+(n-1)d对一切n∈N+都成立。
证明:(1)当n=1时,左边=a1,右边=a1,等式是成立的;
(2)假设当n=k时,等式成立,即ak=a1+(k-1)d,
那么ak+1=ak+d=[a1+(k-1)d]+d=a1+kd,
这就是说,当n=k+1时,等式也成立,
由(1)和(2)可以断定,等式对任何n∈N+都成立。
例2
用数学归纳法证明:1+3+5+…+(2n-1)=n2。
证明:(1)当n=1时,左边=1,右边=1,等式成立;
(2)假设当n=k时,等式成立,即1+3+5+…+(2k-1)=k2。
那么1+3+5+…+(2k-1)+[2(k+1)-1]
=k2+[2(k+1)-1]=k2+2k+1=(k+1)2。
这就是说,当n=k+1时,等式也成立,
由(1)和(2)可以断定,等式对任何n∈N+都成立。
类型五 数列极限
(1)简单型极限——直接法:
当堂训练
设等差数列{an}的公差为d,由前n项和的概念及已知条件得
=9(2a1+d),
①
4a1+6d=4(2a1+d
)。
②
由②得d=2a1,代入①有
=36a1,
解得a1=0或a1=36。
将a1=0舍去。因此a1=36,d=72,
故数列{an}的通项公式an=36+(n-1)·72=72n-36=36(2n-1)。
1.设数列{an}是公差不为零的等差数列,Sn是数列{an}的前n项和(n∈N+),且
=9S2,S4=4S2,则数列{an}的通项公式是_____________。
答案
解析
an=36(2n-1)
2.若数列{an}的前n项和Sn=
n2-
n(n=1,2,3,…),则此数列的通项公
式为__________;数列{nan}中数值最小的项是第__项。
答案
解析
an=3n-16
3
所以n=3时,nan的值最小。
3.设等差数列{an}的前n项和为Sn,公比是正数的等比数列{bn}的前n项和为Tn,已知a1=1,b1=3,a3+b3=17,T3-S3=12,求{an}、{bn}的通项公式。
解答
设数列{an}的公差为d,数列{bn}的公比为q。
由a3+b3=17得1+2d+3q2=17,
①
由T3-S3=12得q2+q-d=4。
②
由①、②及q>0解得q=2,d=2。
故所求的通项公式为an=2n-1,bn=3·2n-1。
4.用数学归纳法证明:
证明:(1)当n=1时,左边=4,右边=4,因为左边=右边,所以等式是成立的;
(2)假设当n=k时,等式成立,即
这就是说,当n=k+1时,等式也成立,
由(1)和(2)可以断定,等式对任何n∈N+都成立。
6.计算下列数列的极限:
谢
谢
第7章
数列与数学归纳法
复习课件
题型探究
知识梳理
内容索引
当堂训练
知识梳理
知识网络
对比归纳等差数列和等比数列的基本概念和公式
?
等差数列
等比数列
定义
如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫作等差数列,这个常数叫作等差数列的公差,公差通常用字母d表示
如果一个数列从第2项起,每一项与它的前一项的比等于同一常数,那么这个数列叫作等比数列,这个常数叫作等比数列的公比,公比通常用字母q表示(q≠0)
递推公式
an+1-an=d
=q
中项
由三个数a,A,b组成的等差数列可以看成最简单的等差数列。这时A叫作a与b的等差中项,并且A=
如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项,且G=
通项公式
an=a1+(n-1)d
an=a1qn-1
前n项和公式
q≠1时,Sn=
=
,q=1时,Sn=na1
性质
am,an的关系
am-an=(m-n)d
=qm-n
m,n,s,t∈N+,m+n=s+t
am+an=as+at
aman=asat
{kn}是等差数列,且kn∈N+
{
}是等差数列
{
}是等比数列
n=2k-1,k∈N+
S2k-1=(2k-1)·ak
a1a2·…·a2k-1=
判
断
方
法
利用定义
an+1-an是同一常数
是同一常数
利用中项
an+an+2=2an+1
anan+2=
利用通项公式
an=pn+q,其中p、q为常数
an=abn(a≠0,b≠0)
利用前n项和公式
Sn=an2+bn
(a,b为常数)
Sn=A(qn-1),其中A≠0,q≠0且q≠1或Sn=np(p为非零常数)
数学归纳法:对于某些与自然数n有关的命题常常采用下面的方法来证明它的正确性:
先证明当n取第一个值n0时命题成立;然后假设当n=k
(k?N
,k≥n0)时命题成立,证明当n=k+1时命题也成立这种证明方法就叫做数学归纳法
数学归纳法的基本思想:
即先验证使结论有意义的最小的正整数n0,如果当n=n0时,命题成立,再假设当n=k(k≥n0,k∈N
)时,命题成立(这时命题是否成立不是确定的)。根据这个假设,如能推出当n=k+1时,命题也成立,那么就可以递推出对所有不小于n0的正整数n0+1,n0+2,…,命题都成立。
数列极限的描述性定义
读作
“n
趋向于无穷大时,
的极限等于A
”
一般地,在n无限增大的变化过程中,如果
无穷数列
中的项
无限趋近于一个常数A,
那么A叫做数列
的极限,或叫做数列
收敛于A。
(即
无限趋近于0)
记作
(C
是常数)
常用的数列极限
数列极限的运算性质:
前提
无穷等比数列的各项和
首项为a1?0,
公比为?q??1的无穷等比数列的前n项和为Sn,
当n??时Sn的极限,
称为无穷等比数列的各项和。
并用符号S表示,
即:
对于一个m项的有穷数列{an}(n?1,2,……,m),
我们也可以定义其各项和,
即定义为:
对于有穷数列而言,
各项和总是存在的。
题型探究
类型一 方程思想求解数列问题
例1 设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和。已知S3=7,且a1+3,3a2,a3+4构成等差数列。
(1)求数列{an}的通项;
解答
故数列{an}的通项为an=2n-1。
(2)令bn=ln
a3n+1,n=1,2,…,求数列{bn}的前n项和Tn。
解答
由于bn=ln
a3n+1,n=1,2,…,
由(1)得a3n+1=23n,∴bn=ln
23n=3nln
2。
又bn+1-bn=3ln
2,∴{bn}是等差数列,
反思与感悟
在等差数列和等比数列中,通项公式an和前n项和公式Sn共涉及五个量:a1,an,n,q(d),Sn,其中首项a1和公比q(公差d)为基本量,“知三求二”是指将已知条件转换成关于a1,an,n,q(d),Sn的方程组,通过方程的思想解出需要的量。
跟踪训练1 记等差数列
的前n项和为Sn,设S3=12,且2a1,a2,a3
+1成等比数列,求Sn。
解答
类型二 转化与化归思想求解数列问题
例1 在数列{an}中,Sn+1=4an+2,a1=1。
(1)
设cn=
,求证数列{cn}是等差数列;
证明
由Sn+1=4an+2,
①
则当n≥2,n∈N+时,有Sn=4an-1+2
②
①-②得an+1=4an-4an-1
方法一 对an+1=4an-4an-1两边同除以2n+1,得
即cn+1+cn-1=2cn,
∴数列{cn}是等差数列。
由Sn+1=4an+2,得a1+a2=4a1+2,则a2=3a1+2=5,
方法二 ∵an+1-2an=2an-4an-1=2(an-2an-1),
令bn=an+1-2an
则{bn}是以a2-2a1=4a1+2-a1-2a1=3为首项,2为公比的等比数列,
∴bn=3·2n-1
(2)
求数列{an}的通项公式及前n项和的公式。
解答
设Sn=(3-1)·2-1+(3×2-1)·20+…+(3n-1)·2n-2,
∴2Sn=(3-1)·20+(3×2-1)·21+…+(3n-1)·2n-1,
故Sn=2Sn-Sn
=-(3-1)·2-1-3(20+21+…+2n-2)+(3n-1)·2n-1
=-1+3+(3n-4)·2n-1
=2+(3n-4)·2n-1
∴
数列{an}的通项公式为an=(3n-1)·2n-2,前n项和公式为Sn=2+(3n-4)·2n-1,n∈N+。
反思与感悟
由递推公式求通项公式,要求掌握的方法有两种,一种求法是先找出数列的前几项,通过观察、归纳得出,然后证明;另一种是通过变形转化为等差数列或等比数列,再用公式求出。
跟踪训练1 设数列{an}的前n项和为Sn,已知a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N+)。
(1)求a2,a3的值;
∵a1+2a2+3a3+…+nan
=(n-1)Sn+2n(n∈N+),
∴当n=1时,a1=2×1=2;
当n=2时,a1+2a2=(a1+a2)+4,∴a2=4;
当n=3时,a1+2a2+3a3=2(a1+a2+a3)+6,∴a3=8。
解答
(2)求证:数列{Sn+2}是等比数列。
证明
∵a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N
),
①
∴当n≥2时,a1+2a2+3a3+…+(n-1)an-1
=(n-2)Sn-1+2(n-1)。
②
①-②得nan=(n-1)Sn-(n-2)Sn-1+2
=n(Sn-Sn-1)-Sn+2Sn-1+2
=nan-Sn+2Sn-1+2。
∴-Sn+2Sn-1+2=0,即Sn=2Sn-1+2,
∴Sn+2=2(Sn-1+2)。
∵S1+2=4≠0,∴Sn-1+2≠0,
∴
=2,
故{Sn+2}是以4为首项,2为公比的等比数列。
类型三 函数思想求解数列问题
命题角度1 借助函数性质解数列问题
例1 已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别是一个等比数列的第2项、第3项、第4项。
(1)求数列{an}的通项公式;
解答
由题意得(a1+d)(a1+13d)=(a1+4d)2,
整理得2a1d=d2。∵d>0,∴d=2。
∵a1=1。∴an=2n-1
(n∈N+)。
(2)设bn=
(n∈N+),Sn=b1+b2+…+bn,是否存在t,使得对任意的n均有Sn>
总成立?若存在,求出最大的整数t;若不存在,请说明理由。
解答
∴数列{Sn}是递增的。
又∵t∈Z,∴适合条件的t的最大值为8。
反思与感悟
数列是一种特殊的函数,在求解数列问题时,若涉及参数取值范围,最值问题或单调性时,均可考虑采用函数的性质及研究方法指导解题。值得注意的是数列定义域是正整数集或{1,2,3,…,n},这一特殊性对问题结果可能造成影响。
跟踪训练1 已知首项为
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N+),且S3+a3,S5+a5,S4+a4成等差数列。
(1)求数列{an}的通项公式;
解答
设等比数列{an}的公比为q,
因为S3+a3,S5+a5,S4+a4成等差数列,
所以S5+a5-S3-a3=S4+a4-S5-a5,
(2)设Tn=Sn-
(n∈N+),求数列{Tn}最大项的值与最小项的值。
解答
命题角度2 以函数为载体给出数列
例2 已知函数f(x)=2-|x|,无穷数列{an}满足an+1=f(an),n∈N+。
(1)若a1=0,求a2,a3,a4;
解答
由an+1=f(an)?an+1=2-|an|,
a1=0?a2=2,a3=0,a4=2。
(2)若a1>0,且a1,a2,a3成等比数列,求a1的值。
解答
=a1[2-|2-|a1||]?(2-a1)2=a1[2-|2-a1|],
分情况讨论:
反思与感悟
以函数为载体给出数列,只需代入函数式即可转化为数列问题。
跟踪训练2 已知函数f(x)=
,数列{an}满足
a1=1,an+1=
,n∈N+。
(1)求数列{an}的通项公式;
解答
(2)令Tn=a1a2-a2a3+a3a4-a4a5+…-a2na2n+1,求Tn。
解答
Tn=a1a2-a2a3+a3a4-a4a5+…-a2na2n+1
=a2(a1-a3)+a4(a3-a5)+…+a2n(a2n-1-a2n+1)
类型四 数学归纳法
例1
用数学归纳法证明:如果{an}是一个等差数列,公差是d,那么an=a1+(n-1)d对一切n∈N+都成立。
证明:(1)当n=1时,左边=a1,右边=a1,等式是成立的;
(2)假设当n=k时,等式成立,即ak=a1+(k-1)d,
那么ak+1=ak+d=[a1+(k-1)d]+d=a1+kd,
这就是说,当n=k+1时,等式也成立,
由(1)和(2)可以断定,等式对任何n∈N+都成立。
例2
用数学归纳法证明:1+3+5+…+(2n-1)=n2。
证明:(1)当n=1时,左边=1,右边=1,等式成立;
(2)假设当n=k时,等式成立,即1+3+5+…+(2k-1)=k2。
那么1+3+5+…+(2k-1)+[2(k+1)-1]
=k2+[2(k+1)-1]=k2+2k+1=(k+1)2。
这就是说,当n=k+1时,等式也成立,
由(1)和(2)可以断定,等式对任何n∈N+都成立。
类型五 数列极限
(1)简单型极限——直接法:
当堂训练
设等差数列{an}的公差为d,由前n项和的概念及已知条件得
=9(2a1+d),
①
4a1+6d=4(2a1+d
)。
②
由②得d=2a1,代入①有
=36a1,
解得a1=0或a1=36。
将a1=0舍去。因此a1=36,d=72,
故数列{an}的通项公式an=36+(n-1)·72=72n-36=36(2n-1)。
1.设数列{an}是公差不为零的等差数列,Sn是数列{an}的前n项和(n∈N+),且
=9S2,S4=4S2,则数列{an}的通项公式是_____________。
答案
解析
an=36(2n-1)
2.若数列{an}的前n项和Sn=
n2-
n(n=1,2,3,…),则此数列的通项公
式为__________;数列{nan}中数值最小的项是第__项。
答案
解析
an=3n-16
3
所以n=3时,nan的值最小。
3.设等差数列{an}的前n项和为Sn,公比是正数的等比数列{bn}的前n项和为Tn,已知a1=1,b1=3,a3+b3=17,T3-S3=12,求{an}、{bn}的通项公式。
解答
设数列{an}的公差为d,数列{bn}的公比为q。
由a3+b3=17得1+2d+3q2=17,
①
由T3-S3=12得q2+q-d=4。
②
由①、②及q>0解得q=2,d=2。
故所求的通项公式为an=2n-1,bn=3·2n-1。
4.用数学归纳法证明:
证明:(1)当n=1时,左边=4,右边=4,因为左边=右边,所以等式是成立的;
(2)假设当n=k时,等式成立,即
这就是说,当n=k+1时,等式也成立,
由(1)和(2)可以断定,等式对任何n∈N+都成立。
6.计算下列数列的极限:
谢
谢
