沪教版(上海)高二数学上册 第8章 平面向量的坐标表示 复习 课件(共24张PPT)
文档属性
| 名称 | 沪教版(上海)高二数学上册 第8章 平面向量的坐标表示 复习 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
第8章
平面向量的坐标表示复习课件
题型探究
知识梳理
内容索引
当堂训练
知识梳理
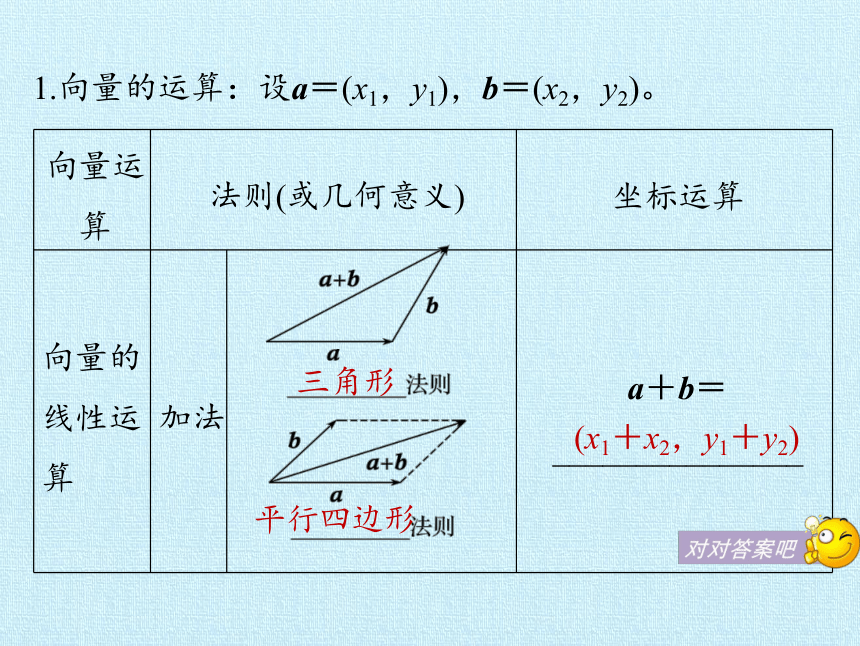
1.向量的运算:设a=(x1,y1),b=(x2,y2)。
向量运算
法则(或几何意义)
坐标运算
向量的线性运算
加法
a+b=_______________
三角形
平行四边形
(x1+x2,y1+y2)
向量的线性运算
减法
a-b=______________
数乘
(1)|λa|=|λ||a|;
(2)当λ>0时,λa的方向与a的方向
;当λ<0时,λa的方向与a的方向
;当λ=0时,λa=0
λa=_________
三角形
(x1-x2,y1-y2)
(λx1,λy1)
相同
相反
向量的数量积运算
a·b=|a||b|cos
θ(θ为a与b的夹角),规定0·a=0,数量积的几何意义是a的模与b在a方向上的射影的积
a·b=_________
x1x2+y1y2
平面向量基本定理
①定理:如果e1,e2是同一平面内的两个
向量,那么对于这一平面内的
向量a,存在唯一对实数λ1,λ2,使a=
。
②基底:把
的向量e1,e2叫作表示这一平面内
向量的一组基底。
不共线
任一
λ1e1+λ2e2
不共线
所有
3.向量的平行与垂直
a,b为非零向量,设a=(x1,y1),b=(x2,y2)。
a∥b
有唯一实数λ使得___________
x1y2-x2y1=0
a⊥b
_______
____________
b=λa(a≠0)
a·b=0
x1x2+y1y2=0
题型探究
类型一 向量的坐标运算
解答
例 已知a=(cos
α,sin
α),b=(cos
β,sin
β),且|ka+b|=
|a-kb|(k>0)。
(1)用k表示数量积a·b;
得(ka+b)2=3(a-kb)2,
∴k2a2+2ka·b+b2=3a2-6ka·b+3k2b2,
∴(k2-3)a2+8ka·b+(1-3k2)b2=0。
∴k2-3+8ka·b+1-3k2=0,
(2)求a·b的最小值,并求出此时a与b的夹角θ的大小。
∴θ=60°。
解答
反思与感悟
数量积运算是向量运算的核心,利用向量数量积可以解决以下问题:
(1)设a=(x1,y1),b=(x2,y2),
a∥b?x1y2-x2y1=0,
a⊥b?x1x2+y1y2=0。
(2)求向量的夹角和模的问题
①设a=(x1,y1),则|a|=
。
②两向量夹角的余弦(0≤θ≤π)
跟踪训练 已知向量
=(3,-4),
=(6,-3),
=(5-m,-(3+m))。
(1)若点A,B,C能构成三角形,求实数m应满足的条件;
解答
解 若点A,B,C能构成三角形,则这三点不共线,
解答
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值。
类型二 向量坐标法在平面几何中的应用
解答
例 已知在等腰△ABC中,BB′,CC′是两腰上的中线,且BB′⊥CC′,求顶角A的余弦值的大小。
解 建立如图所示的平面直角坐标系,
设A(0,a),C(c,0),则B(-c,0),
因为BB′,CC′为AC,AB边上的中线,
反思与感悟
把几何图形放到适当的坐标系中,就赋予了有关点与向量具体的坐标,这样就能进行相应的代数运算和向量运算,从而解决问题。这样的解题方法具有普遍性。
答案
解析
解析 由题意,得∠AOC=90°,故以O为坐标原点,OC,OA所在直线分别为x轴,y轴建立平面直角坐标系,
当堂训练
1.已知向量a=(1,
),b=(3,m)。若向量a,b的夹角为
,则实数m等于
答案
解析
√
答案
解析
解析 由题意可知,△AOB是以O为直角顶点的等腰直角三角形,
3.平面向量a=(
,-1),b=
,若存在不同时为0的实数k和t,使x=a+(t2-3)b,y=-ka+tb,且x⊥y,试求函数关系式k=f(t)。
得a·b=0,|a|=2,|b|=1。
由x⊥y,得[a+(t2-3)b]·(-ka+tb)=0,
-ka2+ta·b-k(t2-3)a·b+t(t2-3)b2=0,
即-4k+t3-3t=0,
解答
谢
谢
第8章
平面向量的坐标表示复习课件
题型探究
知识梳理
内容索引
当堂训练
知识梳理
1.向量的运算:设a=(x1,y1),b=(x2,y2)。
向量运算
法则(或几何意义)
坐标运算
向量的线性运算
加法
a+b=_______________
三角形
平行四边形
(x1+x2,y1+y2)
向量的线性运算
减法
a-b=______________
数乘
(1)|λa|=|λ||a|;
(2)当λ>0时,λa的方向与a的方向
;当λ<0时,λa的方向与a的方向
;当λ=0时,λa=0
λa=_________
三角形
(x1-x2,y1-y2)
(λx1,λy1)
相同
相反
向量的数量积运算
a·b=|a||b|cos
θ(θ为a与b的夹角),规定0·a=0,数量积的几何意义是a的模与b在a方向上的射影的积
a·b=_________
x1x2+y1y2
平面向量基本定理
①定理:如果e1,e2是同一平面内的两个
向量,那么对于这一平面内的
向量a,存在唯一对实数λ1,λ2,使a=
。
②基底:把
的向量e1,e2叫作表示这一平面内
向量的一组基底。
不共线
任一
λ1e1+λ2e2
不共线
所有
3.向量的平行与垂直
a,b为非零向量,设a=(x1,y1),b=(x2,y2)。
a∥b
有唯一实数λ使得___________
x1y2-x2y1=0
a⊥b
_______
____________
b=λa(a≠0)
a·b=0
x1x2+y1y2=0
题型探究
类型一 向量的坐标运算
解答
例 已知a=(cos
α,sin
α),b=(cos
β,sin
β),且|ka+b|=
|a-kb|(k>0)。
(1)用k表示数量积a·b;
得(ka+b)2=3(a-kb)2,
∴k2a2+2ka·b+b2=3a2-6ka·b+3k2b2,
∴(k2-3)a2+8ka·b+(1-3k2)b2=0。
∴k2-3+8ka·b+1-3k2=0,
(2)求a·b的最小值,并求出此时a与b的夹角θ的大小。
∴θ=60°。
解答
反思与感悟
数量积运算是向量运算的核心,利用向量数量积可以解决以下问题:
(1)设a=(x1,y1),b=(x2,y2),
a∥b?x1y2-x2y1=0,
a⊥b?x1x2+y1y2=0。
(2)求向量的夹角和模的问题
①设a=(x1,y1),则|a|=
。
②两向量夹角的余弦(0≤θ≤π)
跟踪训练 已知向量
=(3,-4),
=(6,-3),
=(5-m,-(3+m))。
(1)若点A,B,C能构成三角形,求实数m应满足的条件;
解答
解 若点A,B,C能构成三角形,则这三点不共线,
解答
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值。
类型二 向量坐标法在平面几何中的应用
解答
例 已知在等腰△ABC中,BB′,CC′是两腰上的中线,且BB′⊥CC′,求顶角A的余弦值的大小。
解 建立如图所示的平面直角坐标系,
设A(0,a),C(c,0),则B(-c,0),
因为BB′,CC′为AC,AB边上的中线,
反思与感悟
把几何图形放到适当的坐标系中,就赋予了有关点与向量具体的坐标,这样就能进行相应的代数运算和向量运算,从而解决问题。这样的解题方法具有普遍性。
答案
解析
解析 由题意,得∠AOC=90°,故以O为坐标原点,OC,OA所在直线分别为x轴,y轴建立平面直角坐标系,
当堂训练
1.已知向量a=(1,
),b=(3,m)。若向量a,b的夹角为
,则实数m等于
答案
解析
√
答案
解析
解析 由题意可知,△AOB是以O为直角顶点的等腰直角三角形,
3.平面向量a=(
,-1),b=
,若存在不同时为0的实数k和t,使x=a+(t2-3)b,y=-ka+tb,且x⊥y,试求函数关系式k=f(t)。
得a·b=0,|a|=2,|b|=1。
由x⊥y,得[a+(t2-3)b]·(-ka+tb)=0,
-ka2+ta·b-k(t2-3)a·b+t(t2-3)b2=0,
即-4k+t3-3t=0,
解答
谢
谢
