沪教版(上海)高二数学上册 8.1 向量的坐标表示及其运算_ 课件(共29张PPT)
文档属性
| 名称 | 沪教版(上海)高二数学上册 8.1 向量的坐标表示及其运算_ 课件(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 843.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 00:00:00 | ||
图片预览




文档简介
(共29张PPT)
向量的坐标表示及其运算
一、基本概念
引入:
1.平面内建立了直角坐标系,点A可以用什么来
表示?
2.平面向量是否也有类似的表示呢?
A
(a,b)
a
b
x
y
O
1,在平面直角坐标系中,方向与x轴和y轴正方向分别相同的两个单位向量叫做基本单位向量,分别记为
A
1
1
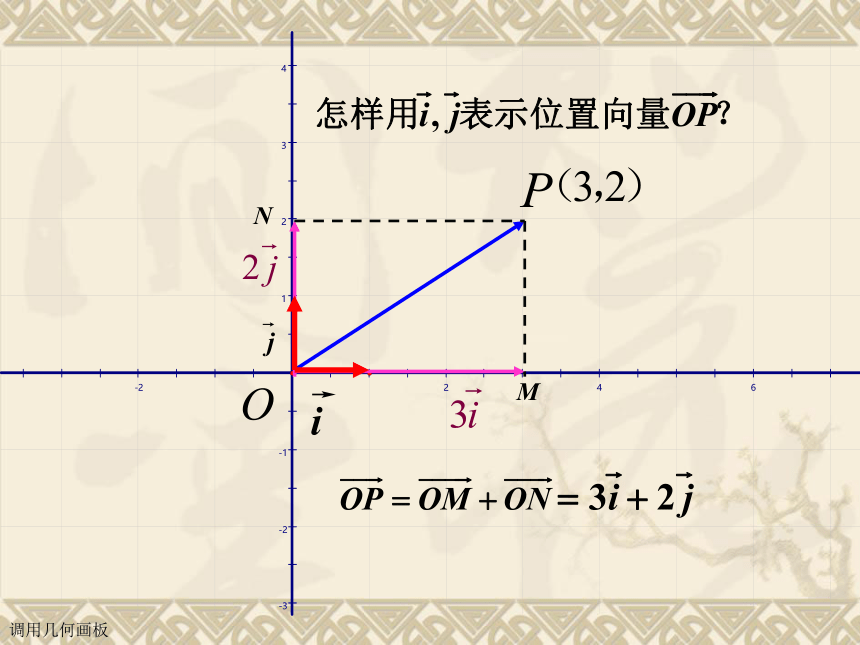
2,以原点O为起点,A为终点的向量
为叫做位置向量,如图,OA即为一个位置向量.
1)平面内每一点都有对应的位置向量。
调用几何画板
x
y
O
M
N
(x,
y)
A
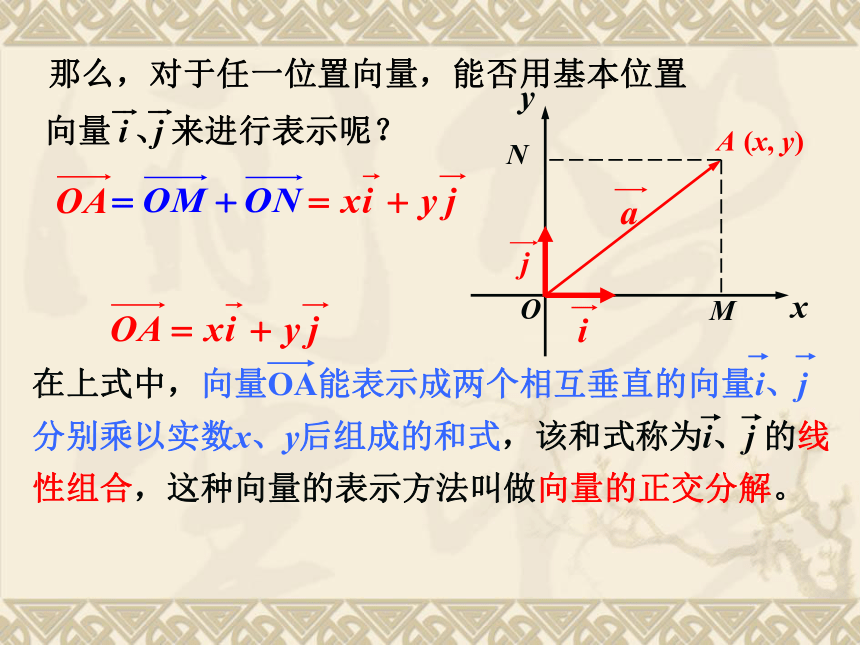
在上式中,向量OA能表示成两个相互垂直的向量i、j
分别乘以实数x、y后组成的和式,该和式称为i、j
的线性组合,这种向量的表示方法叫做向量的正交分解。
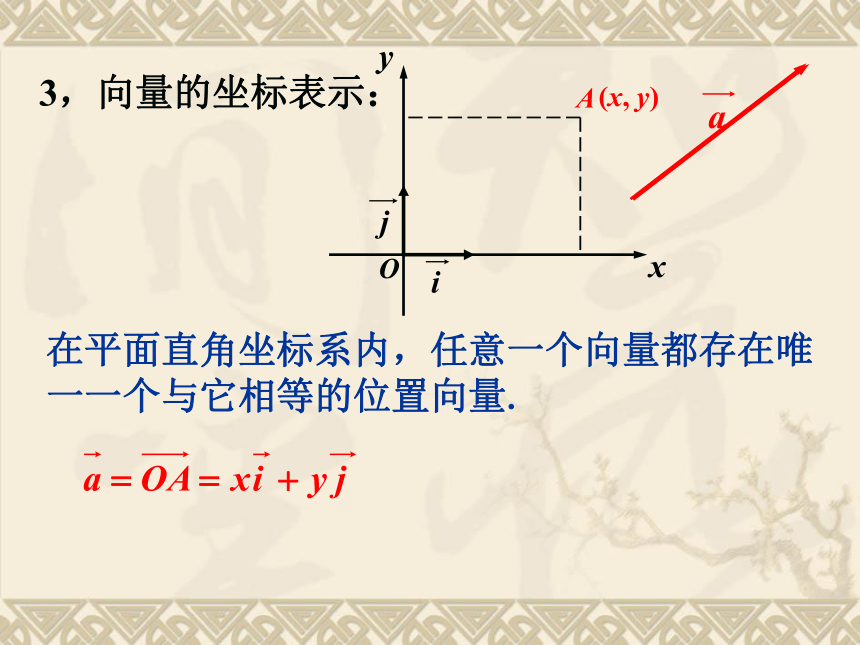
3,向量的坐标表示:
x
y
O
A
在平面直角坐标系内,任意一个向量都存在唯一一个与它相等的位置向量.
(x,
y)
相等的向量具有相同的坐标。
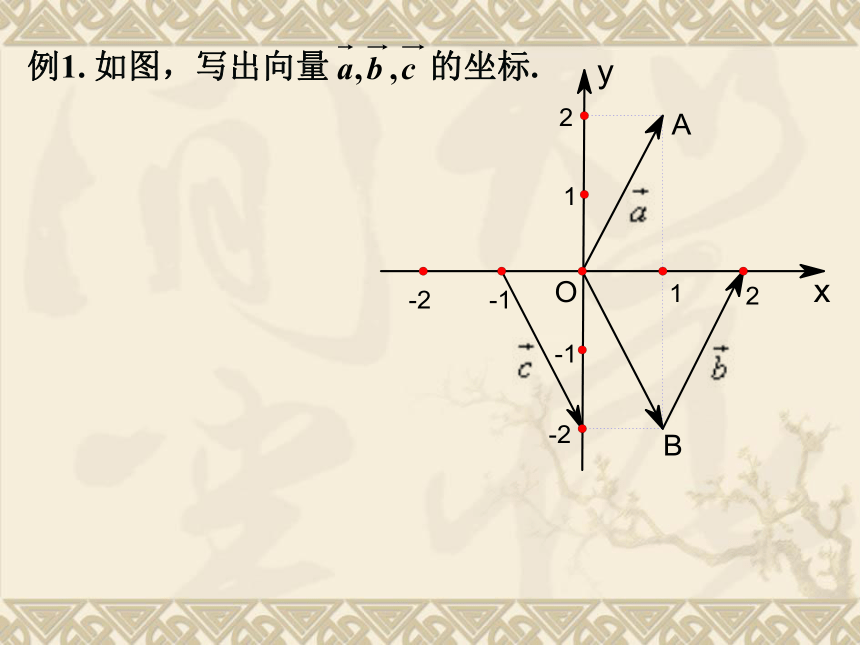
例1.
如图,写出向量
的坐标.
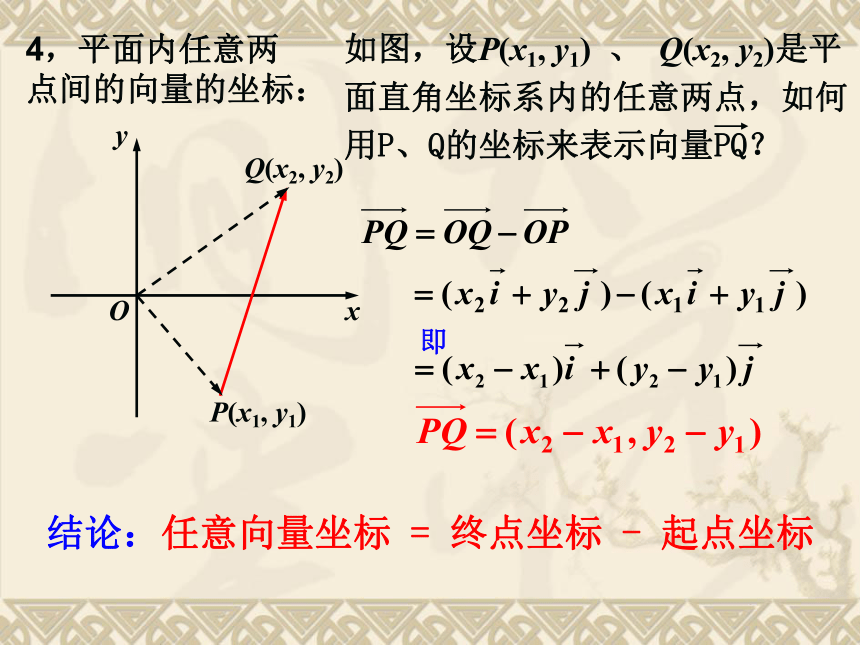
结论:任意向量坐标
=
终点坐标
-
起点坐标
x
y
O
P(x1,
y1)
Q(x2,
y2)
即
如图,设P(x1,
y1)
、
Q(x2,
y2)是平面直角坐标系内的任意两点,如何用P、Q的坐标来表示向量PQ?
4,平面内任意两点间的向量的坐标:
二、向量的坐标运算
5,两个向量和(差)的坐标等于对应坐标的和(差);
数与向量积的坐标等于数与向量对应坐标的积.
x
y
O
A(2,1)
B(-3,2)
C(-1,3)
D(x,y)
练习
若向量
终点Q坐标为(3,0),则向量的始点P坐标为_______
三、向量平行的充要条件的坐标表示
四、定比分点定义及公式
λ
图示
P在线段P1P2反向延长线上
P在线段P1P2延长线上
P在线段P1P2上
外分点
内分点
分点的位置
P
P
P
1
2
P
P
P
1
2
P
P
P
1
2
练习:
设线段 的长为5cm,写出点P分有向线段
所成的比 :
①点P在
上,
=1cm;
②点P在
的延长线上,
=10cm.
例:已知
的坐标分别为
,求点P的坐标
。
已知A(3,2),B(-8,3)
①求线段AB的中点G坐标
②求点A关于点B的对称点H的坐标
⑤若
,求点E的坐标
③若点C分有向线段
AB
的比 =2,求点C的坐标
④求点D(0.5,y)分有向线段
AB
的比
及y值。
向量的坐标表示及其运算
一、基本概念
引入:
1.平面内建立了直角坐标系,点A可以用什么来
表示?
2.平面向量是否也有类似的表示呢?
A
(a,b)
a
b
x
y
O
1,在平面直角坐标系中,方向与x轴和y轴正方向分别相同的两个单位向量叫做基本单位向量,分别记为
A
1
1
2,以原点O为起点,A为终点的向量
为叫做位置向量,如图,OA即为一个位置向量.
1)平面内每一点都有对应的位置向量。
调用几何画板
x
y
O
M
N
(x,
y)
A
在上式中,向量OA能表示成两个相互垂直的向量i、j
分别乘以实数x、y后组成的和式,该和式称为i、j
的线性组合,这种向量的表示方法叫做向量的正交分解。
3,向量的坐标表示:
x
y
O
A
在平面直角坐标系内,任意一个向量都存在唯一一个与它相等的位置向量.
(x,
y)
相等的向量具有相同的坐标。
例1.
如图,写出向量
的坐标.
结论:任意向量坐标
=
终点坐标
-
起点坐标
x
y
O
P(x1,
y1)
Q(x2,
y2)
即
如图,设P(x1,
y1)
、
Q(x2,
y2)是平面直角坐标系内的任意两点,如何用P、Q的坐标来表示向量PQ?
4,平面内任意两点间的向量的坐标:
二、向量的坐标运算
5,两个向量和(差)的坐标等于对应坐标的和(差);
数与向量积的坐标等于数与向量对应坐标的积.
x
y
O
A(2,1)
B(-3,2)
C(-1,3)
D(x,y)
练习
若向量
终点Q坐标为(3,0),则向量的始点P坐标为_______
三、向量平行的充要条件的坐标表示
四、定比分点定义及公式
λ
图示
P在线段P1P2反向延长线上
P在线段P1P2延长线上
P在线段P1P2上
外分点
内分点
分点的位置
P
P
P
1
2
P
P
P
1
2
P
P
P
1
2
练习:
设线段 的长为5cm,写出点P分有向线段
所成的比 :
①点P在
上,
=1cm;
②点P在
的延长线上,
=10cm.
例:已知
的坐标分别为
,求点P的坐标
。
已知A(3,2),B(-8,3)
①求线段AB的中点G坐标
②求点A关于点B的对称点H的坐标
⑤若
,求点E的坐标
③若点C分有向线段
AB
的比 =2,求点C的坐标
④求点D(0.5,y)分有向线段
AB
的比
及y值。
