沪教版(上海)高二数学上册 7.7数列的极限 课件(共24张PPT)
文档属性
| 名称 | 沪教版(上海)高二数学上册 7.7数列的极限 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 493.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
……
项数n
项
1
2
3
4
5
6
7
8
…
…
…
……
考察下列无穷数列是否有类似的变化趋势?
2
3
7.7
数列的极限
Limits
of
Sequences
一.
数列极限的定义
n趋向无于穷大时,
的极限等于
读作:
一.
数列极限的定义
请同学们找出数列极限定义中一些的关键词,并说说你对它们的理解。
1.判断下面的说法是否正确,并说明理由.
(1)数列
的极限1;
(2)数列
的极限1;
(3)数列
的极限
是—1或者1.
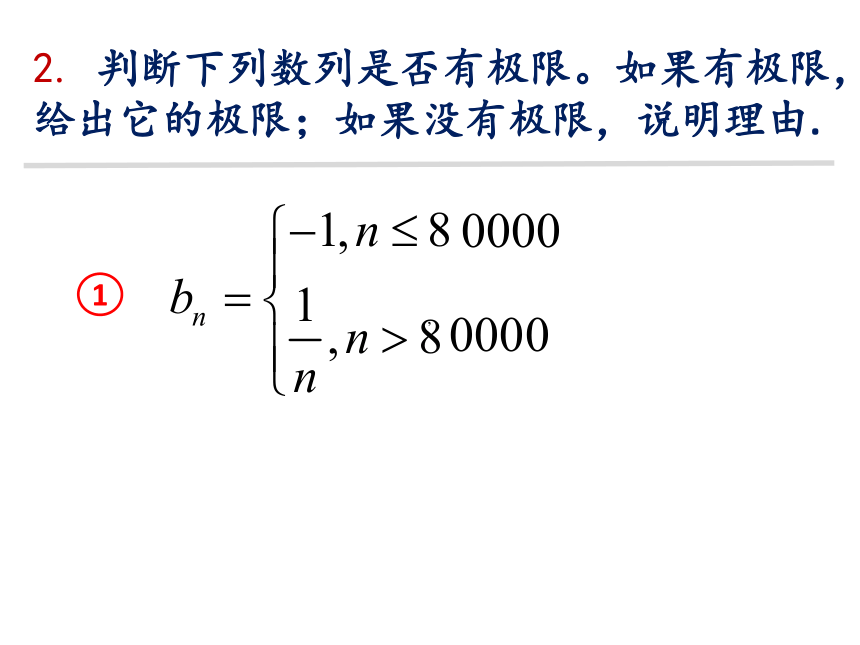
2.
判断下列数列是否有极限。如果有极限,给出它的极限;如果没有极限,说明理由.
1
2.
判断下列数列是否有极限。如果有极限,给出它的极限;如果没有极限,说明理由.
3
2
小结:
1.
数列极限的定义
2.
数列极限的判断方法
……
《庄子》
一尺之棰,
日取其半,
万世不竭。
先秦
"周三径一"
圆周率=圆周与直径的比值
=直径为1的圆的周长
直径为1的圆的周长
魏晋时期
刘徽
割圆术
正六边形
正十二边形
正六边形
正二十四边形
正十二边形
正六边形
割圆术
割之弥细,所失弥少,
割之又割,以至于不可割,
则与圆合体,而无所失矣。
内接正多边形边数
正多边形周长
6
3.00000000
12
3.10582854
24
3.13262861
48
3.13935020
96
3.14103194
192
3.14145247
384
3.14155761
768
3.14158389
1536
3.14159046
3072
3.141592106
…
…
朴素的
直观的
极限观
公元前300多年前
拓展:极限的发展史
17世纪
朴素的
直观的
极限观
公元前300多年前
18世纪
创立了
微积分
拓展:极限的发展史
17世纪
莱布尼兹
(1646-1716)
牛顿
(1643-1727)
朴素的
直观的
极限观
公元前300多年前
18世纪
创立了
微积分
拓展:极限的发展史
19世纪
17世纪
达朗贝尔
(1717-1783)
一个变量趋于一个
固定量,趋于程度
小于任何给定量。
朴素的
直观的
极限观
公元前300多年前
18世纪
创立了
微积分
拓展:极限的发展史
19世纪
17世纪
柯西
(1789-1857)
当一个变量逐次所取的
值无限趋于一个定值,
最终使变量的值和该定
值之差要多小就多小,
这个定值就叫做所有其
它值的极限。
朴素的
直观的
极限观
公元前300多年前
18世纪
创立了
微积分
拓展:极限的发展史
19世纪
严格的
极限理论
17世纪
魏尔斯特拉斯
(1815-1897)
作业:
教材练习7.7(1)
练习册7.7(A)1-7,(B)1,2
阅读材料——数列极限的发展史
……
项数n
项
1
2
3
4
5
6
7
8
…
…
…
……
考察下列无穷数列是否有类似的变化趋势?
2
3
7.7
数列的极限
Limits
of
Sequences
一.
数列极限的定义
n趋向无于穷大时,
的极限等于
读作:
一.
数列极限的定义
请同学们找出数列极限定义中一些的关键词,并说说你对它们的理解。
1.判断下面的说法是否正确,并说明理由.
(1)数列
的极限1;
(2)数列
的极限1;
(3)数列
的极限
是—1或者1.
2.
判断下列数列是否有极限。如果有极限,给出它的极限;如果没有极限,说明理由.
1
2.
判断下列数列是否有极限。如果有极限,给出它的极限;如果没有极限,说明理由.
3
2
小结:
1.
数列极限的定义
2.
数列极限的判断方法
……
《庄子》
一尺之棰,
日取其半,
万世不竭。
先秦
"周三径一"
圆周率=圆周与直径的比值
=直径为1的圆的周长
直径为1的圆的周长
魏晋时期
刘徽
割圆术
正六边形
正十二边形
正六边形
正二十四边形
正十二边形
正六边形
割圆术
割之弥细,所失弥少,
割之又割,以至于不可割,
则与圆合体,而无所失矣。
内接正多边形边数
正多边形周长
6
3.00000000
12
3.10582854
24
3.13262861
48
3.13935020
96
3.14103194
192
3.14145247
384
3.14155761
768
3.14158389
1536
3.14159046
3072
3.141592106
…
…
朴素的
直观的
极限观
公元前300多年前
拓展:极限的发展史
17世纪
朴素的
直观的
极限观
公元前300多年前
18世纪
创立了
微积分
拓展:极限的发展史
17世纪
莱布尼兹
(1646-1716)
牛顿
(1643-1727)
朴素的
直观的
极限观
公元前300多年前
18世纪
创立了
微积分
拓展:极限的发展史
19世纪
17世纪
达朗贝尔
(1717-1783)
一个变量趋于一个
固定量,趋于程度
小于任何给定量。
朴素的
直观的
极限观
公元前300多年前
18世纪
创立了
微积分
拓展:极限的发展史
19世纪
17世纪
柯西
(1789-1857)
当一个变量逐次所取的
值无限趋于一个定值,
最终使变量的值和该定
值之差要多小就多小,
这个定值就叫做所有其
它值的极限。
朴素的
直观的
极限观
公元前300多年前
18世纪
创立了
微积分
拓展:极限的发展史
19世纪
严格的
极限理论
17世纪
魏尔斯特拉斯
(1815-1897)
作业:
教材练习7.7(1)
练习册7.7(A)1-7,(B)1,2
阅读材料——数列极限的发展史
