广东省珠海市2011-2012学年高二下学期期末试题数学文
文档属性
| 名称 | 广东省珠海市2011-2012学年高二下学期期末试题数学文 |  | |
| 格式 | zip | ||
| 文件大小 | 742.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-12 17:05:16 | ||
图片预览




文档简介
珠海市2011-2012学年度第二学期期末学业质量检测
高二文科数学试题
考试用时:120分钟 总分:150分
考试内容:数学选修1-2,数学选修4-4,函数部分内容。
参考公式:
用最小二乘法求线性回归方程系数公式 =, .
随机量变 (其中)
临界值表
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0.455 0.708 1.323 2.072 2.706 3.84 5.024 6.635 7.879 10.83
一、选择题(本题共有12个小题,每小题5分,共60 分).
1.函数的定义域是( )
A. B.
C. D.
2.由①正方形的对角线相等;②平行四边形的对角线相等;③正方形是平行四边形,根据“三段论”推理出一个结论,则这个结论是( )
(A) 正方形的对角线相等 (B) 平行四边形的对角线相等
(C) 正方形是平行四边形 (D)其它
3.计算
A. B. C. D.
4.复数在复平面内对应的点位于( )
(A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限
5.已知,若,则的值是( )
A. B.或 C. D.
6.若直线的参数方程为,则直线的斜率为( )
A. B. C. D.
7.用反证法证明命题:“三角形的内角中至少有一个小于或等于度”时,反设正确的是( )
A.假设三内角都不大于度; B.假设三内角都大于度;
C.假设三内角至多有一个大于度; D.假设三内角至多有两个大于度.
8.以直角坐标系的原点为极点,轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,点的直角坐标是,则点的极坐标可能为( )
A. B. C. D.
9.已知,那么等于( )
A. B. C. D.
10.在同一坐标系中,将椭圆变换成单位圆的伸缩变换是( )
A. B. C. D.
11.用火柴棒按下图的方法搭三角形:
按图示的规律搭下去, 第个图形中火柴棒数是( )
A. B. C. D.
12.下列命题中:
①若,则是纯虚数; ②若且,则;
③复数的模为; ④两个虚数不能比较大小.
其中,正确命题的序号是( )
A.①② B.②④ C.②③ D.①④
二、填空题(本题共有8个小题,每小题5分,共40 分).
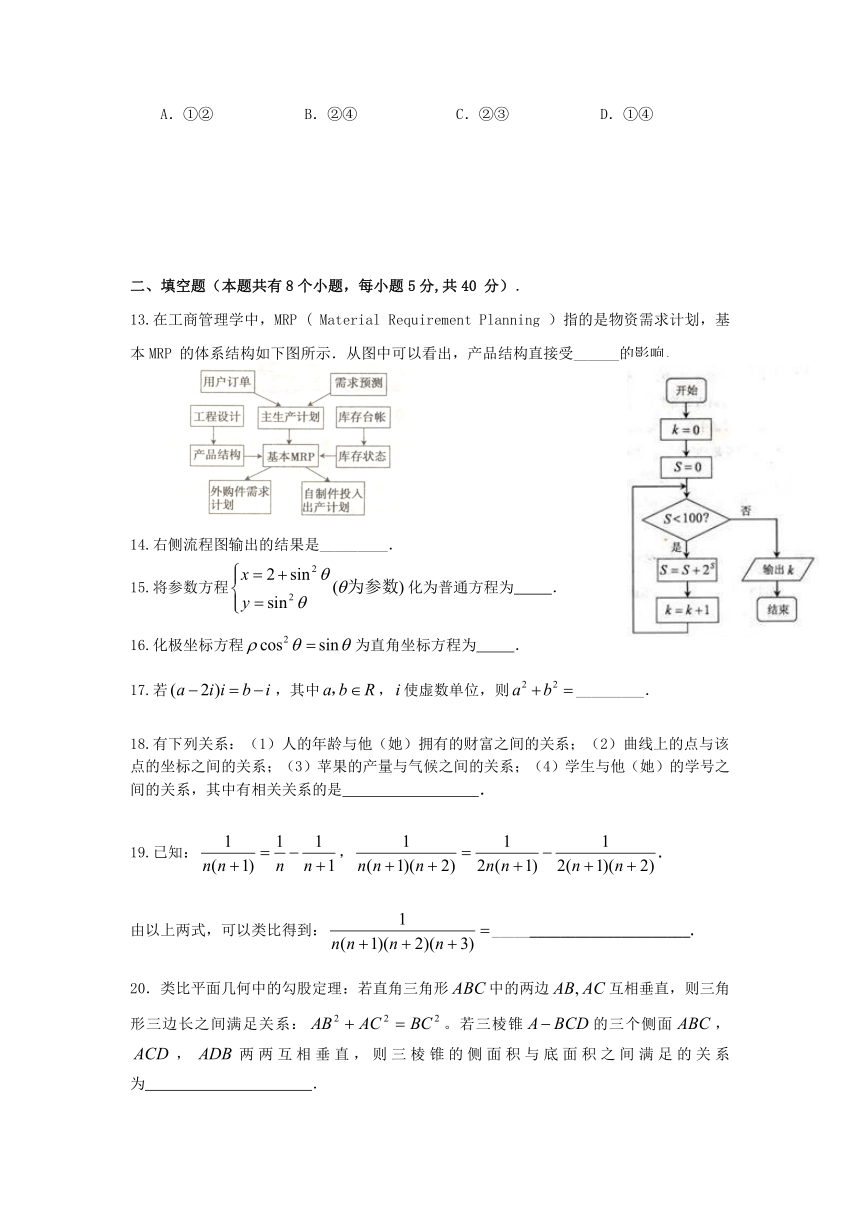
13.在工商管理学中,MRP ( Material Requirement Planning )指的是物资需求计划,基本MRP 的体系结构如下图所示.从图中可以看出,产品结构直接受______的影响.
14.右侧流程图输出的结果是_________.
15.将参数方程化为普通方程为 .
16.化极坐标方程为直角坐标方程为 .
17.若,其中,使虚数单位,则_________.
18.有下列关系:(1)人的年龄与他(她)拥有的财富之间的关系;(2)曲线上的点与该点的坐标之间的关系;(3)苹果的产量与气候之间的关系;(4)学生与他(她)的学号之间的关系,其中有相关关系的是 .
19.已知:,.
由以上两式,可以类比得到:__________________________.
20.类比平面几何中的勾股定理:若直角三角形中的两边互相垂直,则三角形三边长之间满足关系:。若三棱锥的三个侧面,,两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为 .
三、解答题(本题共有5个小题,每小题10分,共50分).
21.(本小题10分)
已知:,求证:
22.(本小题10分)已知直线的极坐标方程为,圆的参数方程为.
(1)求直线和圆的直角坐标方程;
(2)判断直线与圆的位置关系,并说明理由.
23.(本小题10分)
某班主任对全班名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有人,认为作业不多的有人,不喜欢玩电脑游戏的同学认为作业多的有人,认为作业不多的有人.
(1)根据以上数据建立一个的列联表;
(2)你认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?(参考公式及有关数据见卷首,参考数值:,)
24.(本小题10分)
某种产品的广告费用支出(万元)与销售(万元)之间有如下的对应数据:
2 4 5 6 8
30 40 60 50 70
若由资料可知对呈线性相关关系,试求:
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(3)据此估计广告费用支出为10万元时销售收入的值.
25.(本小题10分)
在直角坐标平面上有一点列,对每个正整数,点位于函数的图象上,且的横坐标构成以为首项,为公差的等差数列.
(1)求点的坐标;
(2)设抛物线列中的每一条的对称轴都垂直于轴,第条抛物线
的顶点为且过点,记过点且与抛物线相切的直线
的斜率为,求证:.
高二(文科)数学试题答案分析
考试用时:120分钟 总分:150分
考试内容:数学选修1-2,数学选修4-4,函数部分内容。
参考公式:
用最小二乘法求线性回归方程系数公式 =, .
随机量变 (其中)
临界值表
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0.455 0.708 1.323 2.072 2.706 3.84 5.024 6.635 7.879 10.83
一、选择题(本题共有12个小题,每小题5分,共60 分).
1.(定义域)函数的定义域是( )
A. . C. D.
2.(推理证明)由①正方形的对角线相等;②平行四边形的对角线相等;③正方形是平行四边形,根据“三段论”推理出一个结论,则这个结论是( )
(A) 正方形的对角线相等 (B) 平行四边形的对角线相等(C) 正方形是平行四边形 (D)其它
3.(复数除法)计算
A. B. C. D.
4.(复数概念)复数在复平面内对应的点位于( )
(A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限
5.(分段函数)已知,若,则的值是( )
A. B.或 C. D.
6.(曲线参数方程)若直线的参数方程为,则直线的斜率为( )
A. B. C. D.
7.(反证法)用反证法证明命题:“三角形的内角中至少有一个小于或等于度”时,反设正确的是( )
A.假设三内角都不大于度; B.假设三内角都大于度;
C.假设三内角至多有一个大于度; D.假设三内角至多有两个大于度.
8.(极坐标)以直角坐标系的原点为极点,轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,点的直角坐标是,则点的极坐标可能为( )
A. B. C. D.
9.(解析式)已知,那么等于( )
A. B. C. D.
10.(变换)在同一坐标系中,将椭圆变换成单位圆的伸缩变换是( )
A. B. C. D.
11.(归纳)用火柴棒按下图的方法搭三角形:
按图示的规律搭下去, 第个图形中火柴棒数是( )
A. B. C. D.
12.(复数交汇)下列命题中:
①若,则是纯虚数; ②若且,则;
③复数的模为; ④两个虚数不能比较大小.
其中,正确命题的序号是( )
A.①② B.②④ C.②③ D.①④
二、填空题(本题共有8个小题,每小题5分,共40 分).
13.(结构图)在工商管理学中,MRP ( Material Requirement Planning )指的是物资需求计划,基本MRP 的体系结构如下图所示.从图中可以看出,产品结构直接受______的影响.工程设计
14.(流程图)右侧流程图输出的结果是_________
15.(参数方程)将参数方程化为普通方程为 .
16.(极坐标)化极坐标方程为直角坐标方程为 .
17.(复数)若,其中,使虚数单位,则_________
18.(统计)有下列关系:(1)人的年龄与他(她)拥有的财富之间的关系;(2)曲线上的点与该点的坐标之间的关系;(3)苹果的产量与气候之间的关系;(4)学生与他(她)的学号之间的关系,其中有相关关系的是
19.(类比推理)已知:,.
由以上两式,可以类比得到:__________________________.
20.(类比推理)类比平面几何中的勾股定理:若直角三角形中的两边互相垂直,则三角形三边长之间满足关系:。若三棱锥的三个侧面,,两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为
三、解答题(本题共有5个小题,每小题10分,共50分).
21.(本小题10分)(不等式)
已知:,求证:
证明:
-------------------------------------------------------------1分
-----------------------------------------------------------2分
------------------------------------------------------------3分
-----------------------------------------------------------------4分
-------------------------------------------------------------5分
------------------------------------------------------------------6分
,
----------------------------------------------------------------------7分
显然------------------------------------------------------------------8分
--------------------------------------------------------------9分
即
-----------------------------------------------------10分
22.(本小题10分)(极坐标参数方程)已知直线的极坐标方程为,圆的参数方程为.
(1)求直线和圆的直角坐标方程;
(2)判断直线与圆的位置关系,并说明理由;
解:(1)直线的直角坐标方程为:------------------------------------3分
圆的直角坐标方程为:-------------------------------6分
(2)直线与圆相离
解法一:设圆心到直线的距离为,根据点到直线的距离公式可计算出:
----------------------------------------------------------8分
圆的半径
所以直线与圆相离----------------------------------------------------------10分
解法二:假设圆C与直线有公共点,则有和,将圆C的参数方程代入直线方程,有:
,-----8分
整理得:
,此方程无解,
因此假设不成立,直线与圆相离。-----10分
23.(本小题10分)(列二联表)
某班主任对全班名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有人,认为作业不多的有人,不喜欢玩电脑游戏的同学认为作业多的有人,认为作业不多的有人。
(1)根据以上数据建立一个的列联表;
(2)你认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?(参考公式及有关数据见卷首,参考数值:,)
解:
认为作业多 认为作业不多 合计
喜欢玩电脑游戏 18 9 27
不喜欢玩电脑游戏 8 15 23
合计 26 24 50
------------------------------------------------------------------------------5分
∴的观测值为------------------------------------------7分
-----------------------------------------------------8分
∵--------------------------------------------------------------------9分
通过查表,得到有的把握认为喜欢玩电脑游戏与认为作业多有关系。------------10分
24.(本小题10分)(线性回归直线方程)
某种产品的广告费用支出(万元)与销售(万元)之间有如下的对应数据:
2 4 5 6 8
30 40 60 50 70
若由资料可知对呈线性相关关系,试求:
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(3)据此估计广告费用支出为10万元时销售收入的值.
解:(1)略----------------------------------------------------------------------2分
(2)由题目条件可计算出,--------------------------------------------3分
,----------------------------------------------6分
--------------------------------------------------7分
故y关于x的线性回归方程为---------------------------------------8分
(3)当时, ----------------------------------------------------9分
据此估计广告费用支出为10万元时销售收入为万元-----------------------------10分
25.(本小题10分)(解几数列不等式)
在直角坐标平面上有一点列,对每个正整数,点位于函数的图象上,且的横坐标构成以为首项,为公差的等差数列。
(1)求点的坐标;
(2)设抛物线列中的每一条的对称轴都垂直于轴,第条抛物线
的顶点为且过点,记过点且与抛物线相切的直线
的斜率为,求证:。
解:(1)∵的横坐标构成以为首项,为公差的等差数列,
∴,----------------------------------2分
∵位于函数的图像上,
∴,---------------------------------------3分
∴点的坐标为-----------------------------------------------4分
(2)据题意可设抛物线的方程为:,
即,-------------------------------------------------5分
∵抛物线过点,
∴,
∴,∴,----------------------------------------------6分
∵过点且与抛物线相切的直线即为以为切点的切线,
∴,---------------------------------------7分
∴()-----------------------------8分
∴
-----------------------------------------9分
∴------------------------------10分
1
O
x
y
2
4
3
5
6
7
8
9
10
20
40
30
50
60
1
O
x
y
2
4
3
5
6
7
8
9
10
20
40
30
50
60
高二文科数学试题
考试用时:120分钟 总分:150分
考试内容:数学选修1-2,数学选修4-4,函数部分内容。
参考公式:
用最小二乘法求线性回归方程系数公式 =, .
随机量变 (其中)
临界值表
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0.455 0.708 1.323 2.072 2.706 3.84 5.024 6.635 7.879 10.83
一、选择题(本题共有12个小题,每小题5分,共60 分).
1.函数的定义域是( )
A. B.
C. D.
2.由①正方形的对角线相等;②平行四边形的对角线相等;③正方形是平行四边形,根据“三段论”推理出一个结论,则这个结论是( )
(A) 正方形的对角线相等 (B) 平行四边形的对角线相等
(C) 正方形是平行四边形 (D)其它
3.计算
A. B. C. D.
4.复数在复平面内对应的点位于( )
(A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限
5.已知,若,则的值是( )
A. B.或 C. D.
6.若直线的参数方程为,则直线的斜率为( )
A. B. C. D.
7.用反证法证明命题:“三角形的内角中至少有一个小于或等于度”时,反设正确的是( )
A.假设三内角都不大于度; B.假设三内角都大于度;
C.假设三内角至多有一个大于度; D.假设三内角至多有两个大于度.
8.以直角坐标系的原点为极点,轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,点的直角坐标是,则点的极坐标可能为( )
A. B. C. D.
9.已知,那么等于( )
A. B. C. D.
10.在同一坐标系中,将椭圆变换成单位圆的伸缩变换是( )
A. B. C. D.
11.用火柴棒按下图的方法搭三角形:
按图示的规律搭下去, 第个图形中火柴棒数是( )
A. B. C. D.
12.下列命题中:
①若,则是纯虚数; ②若且,则;
③复数的模为; ④两个虚数不能比较大小.
其中,正确命题的序号是( )
A.①② B.②④ C.②③ D.①④
二、填空题(本题共有8个小题,每小题5分,共40 分).
13.在工商管理学中,MRP ( Material Requirement Planning )指的是物资需求计划,基本MRP 的体系结构如下图所示.从图中可以看出,产品结构直接受______的影响.
14.右侧流程图输出的结果是_________.
15.将参数方程化为普通方程为 .
16.化极坐标方程为直角坐标方程为 .
17.若,其中,使虚数单位,则_________.
18.有下列关系:(1)人的年龄与他(她)拥有的财富之间的关系;(2)曲线上的点与该点的坐标之间的关系;(3)苹果的产量与气候之间的关系;(4)学生与他(她)的学号之间的关系,其中有相关关系的是 .
19.已知:,.
由以上两式,可以类比得到:__________________________.
20.类比平面几何中的勾股定理:若直角三角形中的两边互相垂直,则三角形三边长之间满足关系:。若三棱锥的三个侧面,,两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为 .
三、解答题(本题共有5个小题,每小题10分,共50分).
21.(本小题10分)
已知:,求证:
22.(本小题10分)已知直线的极坐标方程为,圆的参数方程为.
(1)求直线和圆的直角坐标方程;
(2)判断直线与圆的位置关系,并说明理由.
23.(本小题10分)
某班主任对全班名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有人,认为作业不多的有人,不喜欢玩电脑游戏的同学认为作业多的有人,认为作业不多的有人.
(1)根据以上数据建立一个的列联表;
(2)你认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?(参考公式及有关数据见卷首,参考数值:,)
24.(本小题10分)
某种产品的广告费用支出(万元)与销售(万元)之间有如下的对应数据:
2 4 5 6 8
30 40 60 50 70
若由资料可知对呈线性相关关系,试求:
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(3)据此估计广告费用支出为10万元时销售收入的值.
25.(本小题10分)
在直角坐标平面上有一点列,对每个正整数,点位于函数的图象上,且的横坐标构成以为首项,为公差的等差数列.
(1)求点的坐标;
(2)设抛物线列中的每一条的对称轴都垂直于轴,第条抛物线
的顶点为且过点,记过点且与抛物线相切的直线
的斜率为,求证:.
高二(文科)数学试题答案分析
考试用时:120分钟 总分:150分
考试内容:数学选修1-2,数学选修4-4,函数部分内容。
参考公式:
用最小二乘法求线性回归方程系数公式 =, .
随机量变 (其中)
临界值表
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0.455 0.708 1.323 2.072 2.706 3.84 5.024 6.635 7.879 10.83
一、选择题(本题共有12个小题,每小题5分,共60 分).
1.(定义域)函数的定义域是( )
A. . C. D.
2.(推理证明)由①正方形的对角线相等;②平行四边形的对角线相等;③正方形是平行四边形,根据“三段论”推理出一个结论,则这个结论是( )
(A) 正方形的对角线相等 (B) 平行四边形的对角线相等(C) 正方形是平行四边形 (D)其它
3.(复数除法)计算
A. B. C. D.
4.(复数概念)复数在复平面内对应的点位于( )
(A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限
5.(分段函数)已知,若,则的值是( )
A. B.或 C. D.
6.(曲线参数方程)若直线的参数方程为,则直线的斜率为( )
A. B. C. D.
7.(反证法)用反证法证明命题:“三角形的内角中至少有一个小于或等于度”时,反设正确的是( )
A.假设三内角都不大于度; B.假设三内角都大于度;
C.假设三内角至多有一个大于度; D.假设三内角至多有两个大于度.
8.(极坐标)以直角坐标系的原点为极点,轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,点的直角坐标是,则点的极坐标可能为( )
A. B. C. D.
9.(解析式)已知,那么等于( )
A. B. C. D.
10.(变换)在同一坐标系中,将椭圆变换成单位圆的伸缩变换是( )
A. B. C. D.
11.(归纳)用火柴棒按下图的方法搭三角形:
按图示的规律搭下去, 第个图形中火柴棒数是( )
A. B. C. D.
12.(复数交汇)下列命题中:
①若,则是纯虚数; ②若且,则;
③复数的模为; ④两个虚数不能比较大小.
其中,正确命题的序号是( )
A.①② B.②④ C.②③ D.①④
二、填空题(本题共有8个小题,每小题5分,共40 分).
13.(结构图)在工商管理学中,MRP ( Material Requirement Planning )指的是物资需求计划,基本MRP 的体系结构如下图所示.从图中可以看出,产品结构直接受______的影响.工程设计
14.(流程图)右侧流程图输出的结果是_________
15.(参数方程)将参数方程化为普通方程为 .
16.(极坐标)化极坐标方程为直角坐标方程为 .
17.(复数)若,其中,使虚数单位,则_________
18.(统计)有下列关系:(1)人的年龄与他(她)拥有的财富之间的关系;(2)曲线上的点与该点的坐标之间的关系;(3)苹果的产量与气候之间的关系;(4)学生与他(她)的学号之间的关系,其中有相关关系的是
19.(类比推理)已知:,.
由以上两式,可以类比得到:__________________________.
20.(类比推理)类比平面几何中的勾股定理:若直角三角形中的两边互相垂直,则三角形三边长之间满足关系:。若三棱锥的三个侧面,,两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为
三、解答题(本题共有5个小题,每小题10分,共50分).
21.(本小题10分)(不等式)
已知:,求证:
证明:
-------------------------------------------------------------1分
-----------------------------------------------------------2分
------------------------------------------------------------3分
-----------------------------------------------------------------4分
-------------------------------------------------------------5分
------------------------------------------------------------------6分
,
----------------------------------------------------------------------7分
显然------------------------------------------------------------------8分
--------------------------------------------------------------9分
即
-----------------------------------------------------10分
22.(本小题10分)(极坐标参数方程)已知直线的极坐标方程为,圆的参数方程为.
(1)求直线和圆的直角坐标方程;
(2)判断直线与圆的位置关系,并说明理由;
解:(1)直线的直角坐标方程为:------------------------------------3分
圆的直角坐标方程为:-------------------------------6分
(2)直线与圆相离
解法一:设圆心到直线的距离为,根据点到直线的距离公式可计算出:
----------------------------------------------------------8分
圆的半径
所以直线与圆相离----------------------------------------------------------10分
解法二:假设圆C与直线有公共点,则有和,将圆C的参数方程代入直线方程,有:
,-----8分
整理得:
,此方程无解,
因此假设不成立,直线与圆相离。-----10分
23.(本小题10分)(列二联表)
某班主任对全班名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有人,认为作业不多的有人,不喜欢玩电脑游戏的同学认为作业多的有人,认为作业不多的有人。
(1)根据以上数据建立一个的列联表;
(2)你认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?(参考公式及有关数据见卷首,参考数值:,)
解:
认为作业多 认为作业不多 合计
喜欢玩电脑游戏 18 9 27
不喜欢玩电脑游戏 8 15 23
合计 26 24 50
------------------------------------------------------------------------------5分
∴的观测值为------------------------------------------7分
-----------------------------------------------------8分
∵--------------------------------------------------------------------9分
通过查表,得到有的把握认为喜欢玩电脑游戏与认为作业多有关系。------------10分
24.(本小题10分)(线性回归直线方程)
某种产品的广告费用支出(万元)与销售(万元)之间有如下的对应数据:
2 4 5 6 8
30 40 60 50 70
若由资料可知对呈线性相关关系,试求:
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(3)据此估计广告费用支出为10万元时销售收入的值.
解:(1)略----------------------------------------------------------------------2分
(2)由题目条件可计算出,--------------------------------------------3分
,----------------------------------------------6分
--------------------------------------------------7分
故y关于x的线性回归方程为---------------------------------------8分
(3)当时, ----------------------------------------------------9分
据此估计广告费用支出为10万元时销售收入为万元-----------------------------10分
25.(本小题10分)(解几数列不等式)
在直角坐标平面上有一点列,对每个正整数,点位于函数的图象上,且的横坐标构成以为首项,为公差的等差数列。
(1)求点的坐标;
(2)设抛物线列中的每一条的对称轴都垂直于轴,第条抛物线
的顶点为且过点,记过点且与抛物线相切的直线
的斜率为,求证:。
解:(1)∵的横坐标构成以为首项,为公差的等差数列,
∴,----------------------------------2分
∵位于函数的图像上,
∴,---------------------------------------3分
∴点的坐标为-----------------------------------------------4分
(2)据题意可设抛物线的方程为:,
即,-------------------------------------------------5分
∵抛物线过点,
∴,
∴,∴,----------------------------------------------6分
∵过点且与抛物线相切的直线即为以为切点的切线,
∴,---------------------------------------7分
∴()-----------------------------8分
∴
-----------------------------------------9分
∴------------------------------10分
1
O
x
y
2
4
3
5
6
7
8
9
10
20
40
30
50
60
1
O
x
y
2
4
3
5
6
7
8
9
10
20
40
30
50
60
同课章节目录
