22.6(1)三角形的中位线(教案)
图片预览

文档简介
课题:22.6(1)三角形的中位线
授课对象:八(1)班学生 课时数:1课时 设计者:孙莹
教学目标
1.理解三角形的中位线概念,知道三角形的中线和中位线的区别.
2.经历探索三角形中位线性质的过程,体会转化的思想方法.
3.掌握三角形中位线的性质定理,能运用三角形中位线定理进行简单的几何计算和论证.
教学重点及难点
重点:探索三角形的中位线的性质并掌握三角形中位线定理,初步学会用这个定理的运用.
难点:三角形中位线定理证明中添加辅助线的思想方法.
教学用具准备
多媒体课件
课堂探究 师生研疑
教学过程设计
导入新课、提出问题
老师提问:“上课了,你们首先要知道什么?”“通过预习,谁能说说今天我们学什么内容”“要学好今天这节课我们要解决哪些问题”
我的问题:
老师与学生共同梳理问题,确定解决问题的先后顺序。
(预设问题:什么是三角形的中位线 中位线与中线的区别 三角形的中位线定理是什么 三角形中位线定理是怎么证明得出的 有哪些证明方法 怎么添辅助线 学习了三角形的中位线定理可以解决哪些数学问题 等)
反馈已知,自定学习目标
交流预学单的完成情况,了解学生掌握了什么,明确这堂课的学习目标。
尝试探究,师生研疑
用几何画板画三角形的中位线,多媒体演示课本上的操作,并总结证明三角形的中位线性质定理有些方法,请同学展示自己的方法.并通过这些方法的交流发现证明中位线的根据思想是利用三角形全等及平行四边形的性质。
提出新问题:
练习1.已知,如图,D、E、F分别是△ABC三边AB、BC、CA的中点,
若AB=8cm,则EF= cm;
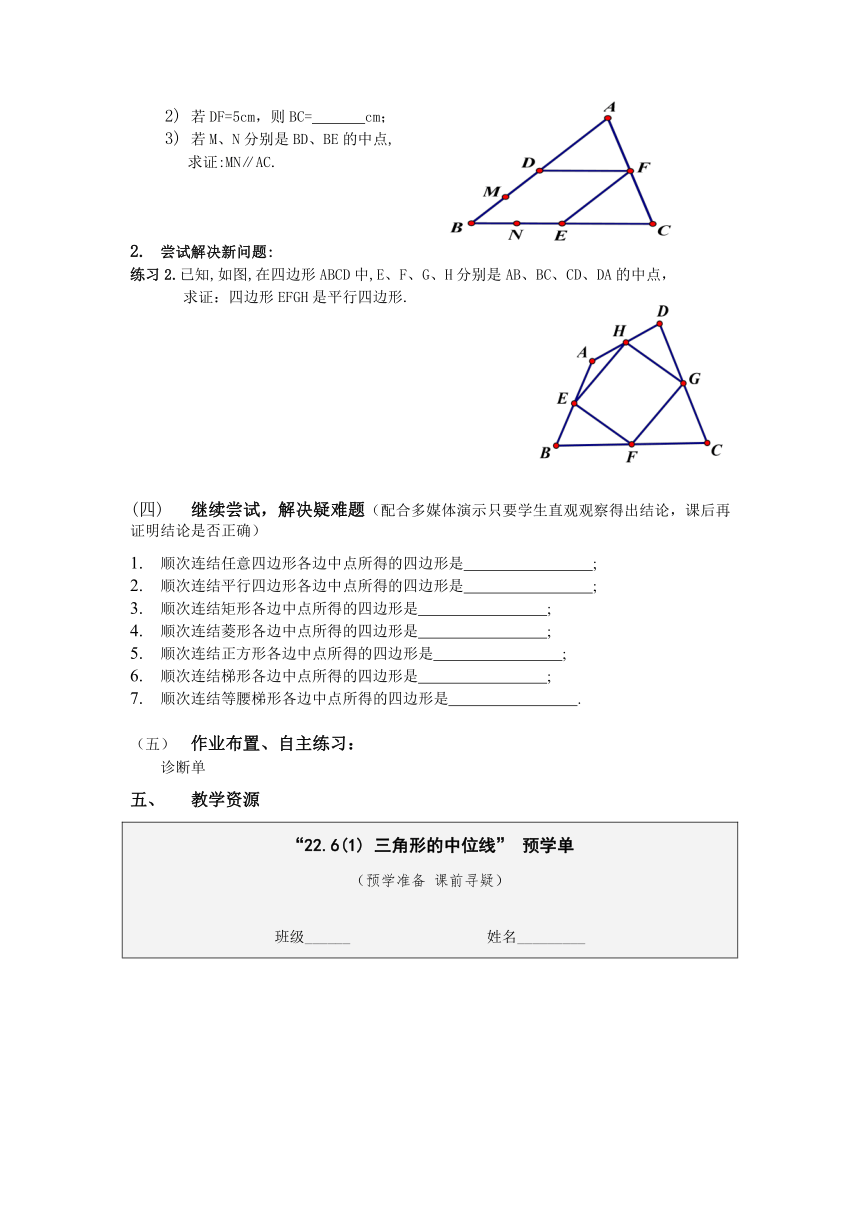
若DF=5cm,则BC= cm;
若M、N分别是BD、BE的中点,
求证:MN∥AC.
尝试解决新问题:
练习2.已知,如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
继续尝试,解决疑难题(配合多媒体演示只要学生直观观察得出结论,课后再证明结论是否正确)
顺次连结任意四边形各边中点所得的四边形是 ;
顺次连结平行四边形各边中点所得的四边形是 ;
顺次连结矩形各边中点所得的四边形是 ;
顺次连结菱形各边中点所得的四边形是 ;
顺次连结正方形各边中点所得的四边形是 ;
顺次连结梯形各边中点所得的四边形是 ;
顺次连结等腰梯形各边中点所得的四边形是 .
作业布置、自主练习:
诊断单
教学资源
“22.6(1) 三角形的中位线” 预学单(预学准备 课前寻疑)班级______ 姓名_________
填空题:联结三角形 的线段叫做三角形的中位线。三角形中位线定理:三角形的中位线平行于 ,并且等于 。其数学表达式为:∵D、E分别是AB、AC的中点 ∴ △ABC中,D、E分别是AB、AC的中点,如果BC=10cm,那么DE= cm。△ABC中,D、E、F分别是AB、AC、BC的中点,如果DE=3cm,EF=5cm,FD=6cm,那么△ABC的周长为 cm。△ABC中,D、E、F分别是AB、AC、BC的中点,如果∠A=90°,那么△DEF是 三角形。△ABC中,D、E分别是AB、AC的中点,那么△ADE与△ABC的比为 。简答题:如图:在△ABC中,D是AC的中点, E是AB的中点,F是OB的中点,G是OC的中点,求证:四边形DEFG是平行四边形。请你证明三角形中位线定理,可以用书上提供的方法,更可以用不同于书上的方法,看看谁想到的方法又好又多。下列图形已知:求证:证明:
“22.6(1) 三角形的中位线” 诊断单(课后作业 巩固深化)班级______ 姓名_________
填空:联结三角形各边中点得到的三角形,它的周长为原三角形周长的 ,面积为原三角形面积的 .三角形的一条中位线分原三角形所成的一个小三角形与一个梯形的面积的比是 .△ABC中,D、E、F分别是AB、BC、CA边上的中点,如果∠A=90°,那么△DEF是 三角形.证明: 顺次连结任意四边形各边中点所得的四边形是平行四边形.证明: 顺次连结矩形各边中点所得的四边形是菱形.证明: 顺次连结菱形各边中点所得的四边形是矩形.证明: 顺次连结正方形各边中点所得的四边形是正方形.如图,在△ABC中,∠BAC=90°,延长BA到点D,使AD=AB,点E、F分别为BC、AC的中点。(1)求证:DF=BE;(2)过点A作AG∥BC交DF于点G,求证AG=DG。
课后反思
这节课内容是三角形的中位线定理,它是在掌握了平行四边形的性质和判定的基础上,综合利用这些知识证明而来的.本节课的重点是三角形中位线定理的应用,难点是利用平行四边形的性质与判定证明三角形的中位线定理,以及复杂图形中通过作辅助线应用三角形中位线定理.与平行四边形的性质、判定相比较,三角形的中位线定理在证明时显得有点难度,它没有直接可以运用的平行四边形,而是引导学生利用“补短”方法构造平行四边形,再利用平行四边形的性质得出答案.所以,课前布置了预习工作,并在早自修时让学生提交了预学单,汇总了一下学生提出的问题,以及批改了预习单上的练习,统计了正确率。发现预学单上对于定理的直接运用绝大部分同学都没有问题,只有个别同学做错,正确率超过90﹪,同学们的困难都是在于如何用有别于书上的方法去证明三角形中位线定理。事实上,让学生认识本节课中所涉及的数学结论,并不困难的,学生能否记住这个结论对其后续学习的影响也不大;但在这节课中所体现出的“发现—证明—拓广”的数学思维方式,对学生学习数学、学习其他知识乃至认识问题都会产生重要的、深远的影响.所以,从这个意义上讲,本节课的“过程”重于“结果”.“让学生经历探索数学问题的过程”就是这节课的教学目的,至于学生能否在经历了这个过程之后正确地得出所谓的数学结论却在其次.所以在课堂上花了不少时间让不同学生介绍他们的证明方法。但疏忽了在介绍完方法后没有把所有的添加辅助线的方法通过课件展现在一个页面上,让学生更清晰完整地回顾五种方法,从而感悟到这些方法的内在联系都是通过添加辅助线使问题转化为平行四边形的问题,因此这堂课其实是一堂“平行四边形的运用”课,故教材把这一节内容放在“平行四边形”这一章内(全国教材就是以“平行四边形的运用”作为这节课的课题的)。如果能达到这个层次那么学生的认知水平又提升了一个档次。这也提醒我看似小小的一个细节有可能是整个教学环节中至关重要的一步。在以后的备课中我还需要多站在学生的角度去设计教学过程。
至于提问题环节,经过较长时间的训练,已略有成效。也是由于数学课的学科特点,学生提的问题不会像语文课那样繁多,更不会不着边际,可能会语言表达不恰当不到位,但这不难训练。本节课所涉及到的问题大多属于常规问题,所以该环节比较顺利,但在今后的教学过程中不能只局限于常规问题,还要继续学生如何提出更有质量更直击教学本质的问题,从而使学生的元认知得到提高。
本课最后一串疑难题,之所以设定为疑难题也是因为没有打算让他们这节课完全解决,为了降低难度,我通过课件上图形形状的改变,让学生直观地判断所得四边形的形状,然后结合课后检测单中的练习去证明他们的结论是否正确,为下一节练习课作了铺垫,最终学生自己获得“所得四边形的形状是由原四边形的对角线的位置关系和数量关系所决定的”这一结论。
这节课是一次全新的尝试,是本学期开展问题化学习以后的一次成果展示,心里仍是忐忑的,不知道自己对于问题化学习的理解是否正确,这样的课堂是不是就是问题化学习的课堂。学生在问题化学习后是否学习效率、学习效果都能提升,怎样训练学生有效预习、怎样设计和控制预学单与检测单的质与量,都是我在思考的问题,希望下学期我和我的孩子们都有更大的收获。
授课对象:八(1)班学生 课时数:1课时 设计者:孙莹
教学目标
1.理解三角形的中位线概念,知道三角形的中线和中位线的区别.
2.经历探索三角形中位线性质的过程,体会转化的思想方法.
3.掌握三角形中位线的性质定理,能运用三角形中位线定理进行简单的几何计算和论证.
教学重点及难点
重点:探索三角形的中位线的性质并掌握三角形中位线定理,初步学会用这个定理的运用.
难点:三角形中位线定理证明中添加辅助线的思想方法.
教学用具准备
多媒体课件
课堂探究 师生研疑
教学过程设计
导入新课、提出问题
老师提问:“上课了,你们首先要知道什么?”“通过预习,谁能说说今天我们学什么内容”“要学好今天这节课我们要解决哪些问题”
我的问题:
老师与学生共同梳理问题,确定解决问题的先后顺序。
(预设问题:什么是三角形的中位线 中位线与中线的区别 三角形的中位线定理是什么 三角形中位线定理是怎么证明得出的 有哪些证明方法 怎么添辅助线 学习了三角形的中位线定理可以解决哪些数学问题 等)
反馈已知,自定学习目标
交流预学单的完成情况,了解学生掌握了什么,明确这堂课的学习目标。
尝试探究,师生研疑
用几何画板画三角形的中位线,多媒体演示课本上的操作,并总结证明三角形的中位线性质定理有些方法,请同学展示自己的方法.并通过这些方法的交流发现证明中位线的根据思想是利用三角形全等及平行四边形的性质。
提出新问题:
练习1.已知,如图,D、E、F分别是△ABC三边AB、BC、CA的中点,
若AB=8cm,则EF= cm;
若DF=5cm,则BC= cm;
若M、N分别是BD、BE的中点,
求证:MN∥AC.
尝试解决新问题:
练习2.已知,如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形.
继续尝试,解决疑难题(配合多媒体演示只要学生直观观察得出结论,课后再证明结论是否正确)
顺次连结任意四边形各边中点所得的四边形是 ;
顺次连结平行四边形各边中点所得的四边形是 ;
顺次连结矩形各边中点所得的四边形是 ;
顺次连结菱形各边中点所得的四边形是 ;
顺次连结正方形各边中点所得的四边形是 ;
顺次连结梯形各边中点所得的四边形是 ;
顺次连结等腰梯形各边中点所得的四边形是 .
作业布置、自主练习:
诊断单
教学资源
“22.6(1) 三角形的中位线” 预学单(预学准备 课前寻疑)班级______ 姓名_________
填空题:联结三角形 的线段叫做三角形的中位线。三角形中位线定理:三角形的中位线平行于 ,并且等于 。其数学表达式为:∵D、E分别是AB、AC的中点 ∴ △ABC中,D、E分别是AB、AC的中点,如果BC=10cm,那么DE= cm。△ABC中,D、E、F分别是AB、AC、BC的中点,如果DE=3cm,EF=5cm,FD=6cm,那么△ABC的周长为 cm。△ABC中,D、E、F分别是AB、AC、BC的中点,如果∠A=90°,那么△DEF是 三角形。△ABC中,D、E分别是AB、AC的中点,那么△ADE与△ABC的比为 。简答题:如图:在△ABC中,D是AC的中点, E是AB的中点,F是OB的中点,G是OC的中点,求证:四边形DEFG是平行四边形。请你证明三角形中位线定理,可以用书上提供的方法,更可以用不同于书上的方法,看看谁想到的方法又好又多。下列图形已知:求证:证明:
“22.6(1) 三角形的中位线” 诊断单(课后作业 巩固深化)班级______ 姓名_________
填空:联结三角形各边中点得到的三角形,它的周长为原三角形周长的 ,面积为原三角形面积的 .三角形的一条中位线分原三角形所成的一个小三角形与一个梯形的面积的比是 .△ABC中,D、E、F分别是AB、BC、CA边上的中点,如果∠A=90°,那么△DEF是 三角形.证明: 顺次连结任意四边形各边中点所得的四边形是平行四边形.证明: 顺次连结矩形各边中点所得的四边形是菱形.证明: 顺次连结菱形各边中点所得的四边形是矩形.证明: 顺次连结正方形各边中点所得的四边形是正方形.如图,在△ABC中,∠BAC=90°,延长BA到点D,使AD=AB,点E、F分别为BC、AC的中点。(1)求证:DF=BE;(2)过点A作AG∥BC交DF于点G,求证AG=DG。
课后反思
这节课内容是三角形的中位线定理,它是在掌握了平行四边形的性质和判定的基础上,综合利用这些知识证明而来的.本节课的重点是三角形中位线定理的应用,难点是利用平行四边形的性质与判定证明三角形的中位线定理,以及复杂图形中通过作辅助线应用三角形中位线定理.与平行四边形的性质、判定相比较,三角形的中位线定理在证明时显得有点难度,它没有直接可以运用的平行四边形,而是引导学生利用“补短”方法构造平行四边形,再利用平行四边形的性质得出答案.所以,课前布置了预习工作,并在早自修时让学生提交了预学单,汇总了一下学生提出的问题,以及批改了预习单上的练习,统计了正确率。发现预学单上对于定理的直接运用绝大部分同学都没有问题,只有个别同学做错,正确率超过90﹪,同学们的困难都是在于如何用有别于书上的方法去证明三角形中位线定理。事实上,让学生认识本节课中所涉及的数学结论,并不困难的,学生能否记住这个结论对其后续学习的影响也不大;但在这节课中所体现出的“发现—证明—拓广”的数学思维方式,对学生学习数学、学习其他知识乃至认识问题都会产生重要的、深远的影响.所以,从这个意义上讲,本节课的“过程”重于“结果”.“让学生经历探索数学问题的过程”就是这节课的教学目的,至于学生能否在经历了这个过程之后正确地得出所谓的数学结论却在其次.所以在课堂上花了不少时间让不同学生介绍他们的证明方法。但疏忽了在介绍完方法后没有把所有的添加辅助线的方法通过课件展现在一个页面上,让学生更清晰完整地回顾五种方法,从而感悟到这些方法的内在联系都是通过添加辅助线使问题转化为平行四边形的问题,因此这堂课其实是一堂“平行四边形的运用”课,故教材把这一节内容放在“平行四边形”这一章内(全国教材就是以“平行四边形的运用”作为这节课的课题的)。如果能达到这个层次那么学生的认知水平又提升了一个档次。这也提醒我看似小小的一个细节有可能是整个教学环节中至关重要的一步。在以后的备课中我还需要多站在学生的角度去设计教学过程。
至于提问题环节,经过较长时间的训练,已略有成效。也是由于数学课的学科特点,学生提的问题不会像语文课那样繁多,更不会不着边际,可能会语言表达不恰当不到位,但这不难训练。本节课所涉及到的问题大多属于常规问题,所以该环节比较顺利,但在今后的教学过程中不能只局限于常规问题,还要继续学生如何提出更有质量更直击教学本质的问题,从而使学生的元认知得到提高。
本课最后一串疑难题,之所以设定为疑难题也是因为没有打算让他们这节课完全解决,为了降低难度,我通过课件上图形形状的改变,让学生直观地判断所得四边形的形状,然后结合课后检测单中的练习去证明他们的结论是否正确,为下一节练习课作了铺垫,最终学生自己获得“所得四边形的形状是由原四边形的对角线的位置关系和数量关系所决定的”这一结论。
这节课是一次全新的尝试,是本学期开展问题化学习以后的一次成果展示,心里仍是忐忑的,不知道自己对于问题化学习的理解是否正确,这样的课堂是不是就是问题化学习的课堂。学生在问题化学习后是否学习效率、学习效果都能提升,怎样训练学生有效预习、怎样设计和控制预学单与检测单的质与量,都是我在思考的问题,希望下学期我和我的孩子们都有更大的收获。
