5.1.1相交线课件(人教新课标七年级下)
文档属性
| 名称 | 5.1.1相交线课件(人教新课标七年级下) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-12 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
我们日常生活中有哪些直线
相交的实际例子?
5.1.1相交线
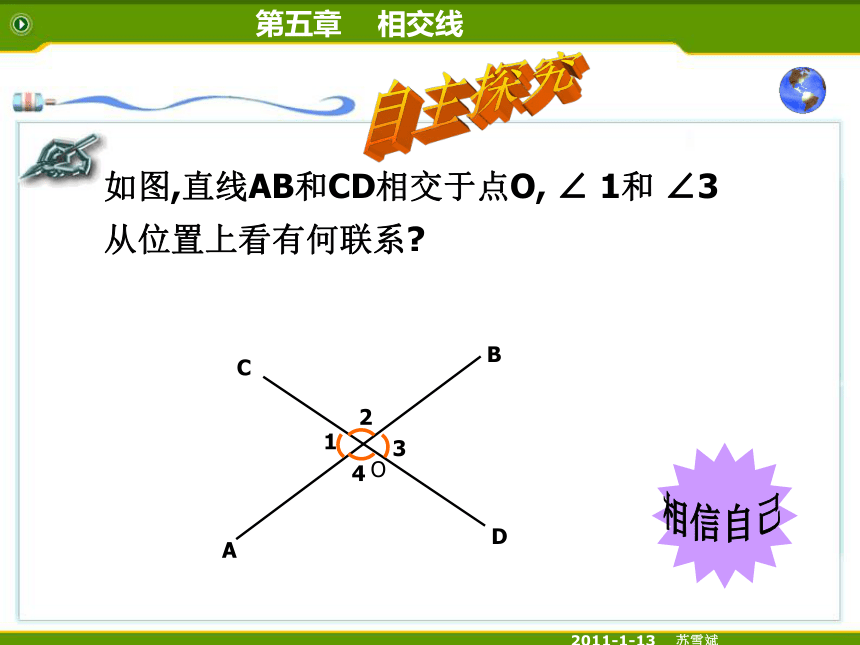
如图,直线AB和CD相交于点O, ∠ 1和 ∠3
从位置上看有何联系
B
A
D
C
O
1
2
3
4
5.1.1相交线
3
3
4
4
1
相等
相对
互补
相邻
4
2
5.1.1相交线
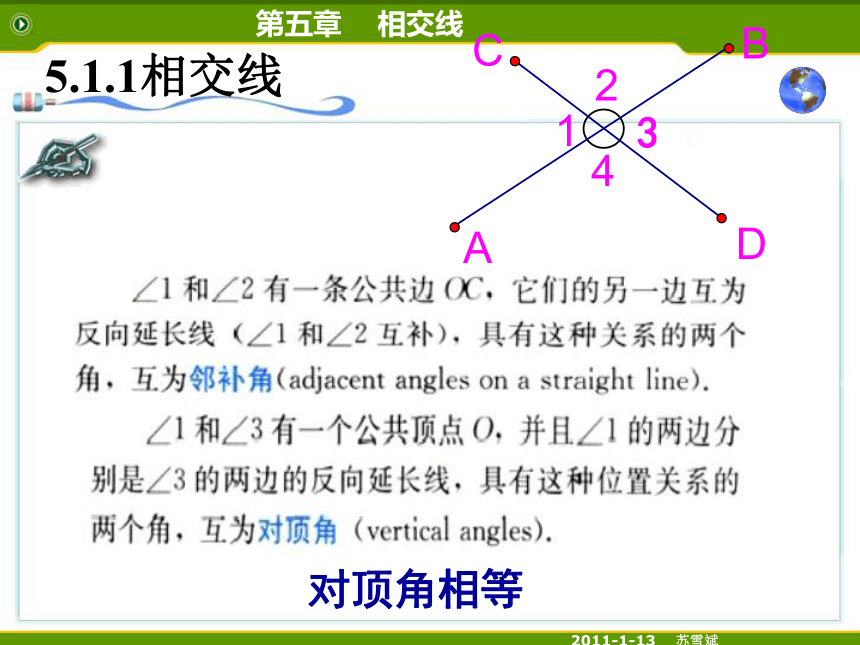
对顶角相等
5.1.1相交线
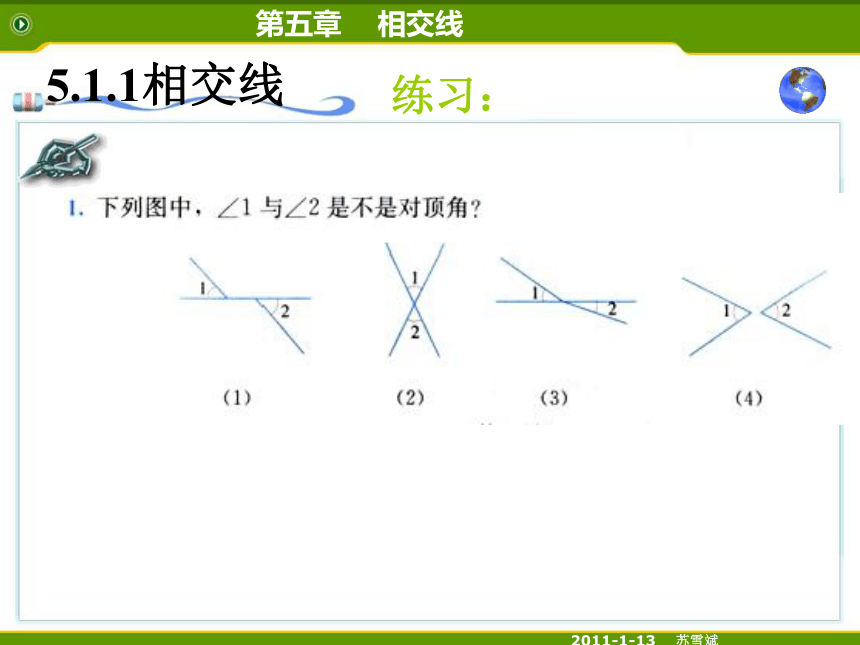
练习:
5.1.1相交线
5.1.1相交线
变式练习
变式1:若∠2是∠1的3倍,求∠3的度数?
变式2:若∠2-∠1=400, 求∠4的度数?
a
b
1
2
3
4
1
2
邻补角是有特殊位置关系的两个互补的角。
1
2
∠1、∠2的和是多少度?∠1和∠2还是补角吗?∠1和∠2还是邻补角吗?
∠1、∠2还是邻补角吗?
例2:如图,已知直线AD与BE相交于点O,
∠DOE与∠COE互余,∠COE=62°
求∠AOB的度数.
A
B
C
D
E
O
3、已知∠A与∠ B是一对邻补角,且∠ B比∠ A小24°,求∠ A和∠ B的度数.
5.1.1相交线
思考:
这节课我们认识了两条相交直线,研究了
与相交线有关的角的问题,相交线构成的角
可分为哪两类?这两类角有什么特点?能举个
利用对顶角解决实际问题的例子吗?
2.两条直线相交得到四个角,其中一个角是30°,则其余
的三个角的度数分别是______________________.
1.若∠α与∠β是对顶角, ∠α=16 °, 则∠β=_____度
16
课堂探究
150 ° 30 ° 150 °
3.图中共有几组对顶角
B
A
C
4.如图,直线AB,CD相交于点O,且
∠AOC+∠BOD=100°,
求∠AOD的度数
A
C
B
D
O
第4题
3.如图,直线AB,CD相交于点O,射线OE
平分∠AOD.已知∠EOD=60°,则
∠COB=_____度, ∠BOD=_____度
A
B
C
D
E
O
第3题
120
60
课堂探究
观察下图,请你与同学合作寻找对顶角,探究出其中的规律:
交于一点的直线的条数
2
3
4
5
…
2005
…
n
对顶角
的对数
课外拓展
如图,直线AB,CD交于点O,OE平分∠ AOD,
∠ BOC= ∠ BOD-30°,求∠ COE的度数.
解:设∠ BOC的度数为 x ° ,
∠ BOD的度数为y ° ,依题意,得
Y+x=180且x=y-30.
解得 x=75 ,y=105 .
所以∠ AOD = ∠ BOC =75 ° , ∠ DOE=1/2
∠ AOD=1/2×75 ° =37.5 ° ,
所以∠ COE =180 ° - ∠ DOE =180 °-37.5 ° =142.5 °
补充练习:
本节课你有何收获?
1.相交线,交点
2.对顶角的顶点相同,角的两边互为反向延长线
3.对顶角相等,邻补角互补.
归纳小结
①两条直线相交形成的角
②有一个公共顶点;
③没有公共边
①两条直线相交而成;
②有一个公共点;
③有一条公共边
对顶
角相
等
角的名称 特 征 性 质 相 同 点 不 同 点
对顶角
邻补角
邻补
角互
补
①都是两条直线相交而成的 角;
②都有一个公共顶点;
③都是成对出现的
①有无公共边
②两直线相交时,
对顶角只有一对
邻补角有两个
我们日常生活中有哪些直线
相交的实际例子?
5.1.1相交线
如图,直线AB和CD相交于点O, ∠ 1和 ∠3
从位置上看有何联系
B
A
D
C
O
1
2
3
4
5.1.1相交线
3
3
4
4
1
相等
相对
互补
相邻
4
2
5.1.1相交线
对顶角相等
5.1.1相交线
练习:
5.1.1相交线
5.1.1相交线
变式练习
变式1:若∠2是∠1的3倍,求∠3的度数?
变式2:若∠2-∠1=400, 求∠4的度数?
a
b
1
2
3
4
1
2
邻补角是有特殊位置关系的两个互补的角。
1
2
∠1、∠2的和是多少度?∠1和∠2还是补角吗?∠1和∠2还是邻补角吗?
∠1、∠2还是邻补角吗?
例2:如图,已知直线AD与BE相交于点O,
∠DOE与∠COE互余,∠COE=62°
求∠AOB的度数.
A
B
C
D
E
O
3、已知∠A与∠ B是一对邻补角,且∠ B比∠ A小24°,求∠ A和∠ B的度数.
5.1.1相交线
思考:
这节课我们认识了两条相交直线,研究了
与相交线有关的角的问题,相交线构成的角
可分为哪两类?这两类角有什么特点?能举个
利用对顶角解决实际问题的例子吗?
2.两条直线相交得到四个角,其中一个角是30°,则其余
的三个角的度数分别是______________________.
1.若∠α与∠β是对顶角, ∠α=16 °, 则∠β=_____度
16
课堂探究
150 ° 30 ° 150 °
3.图中共有几组对顶角
B
A
C
4.如图,直线AB,CD相交于点O,且
∠AOC+∠BOD=100°,
求∠AOD的度数
A
C
B
D
O
第4题
3.如图,直线AB,CD相交于点O,射线OE
平分∠AOD.已知∠EOD=60°,则
∠COB=_____度, ∠BOD=_____度
A
B
C
D
E
O
第3题
120
60
课堂探究
观察下图,请你与同学合作寻找对顶角,探究出其中的规律:
交于一点的直线的条数
2
3
4
5
…
2005
…
n
对顶角
的对数
课外拓展
如图,直线AB,CD交于点O,OE平分∠ AOD,
∠ BOC= ∠ BOD-30°,求∠ COE的度数.
解:设∠ BOC的度数为 x ° ,
∠ BOD的度数为y ° ,依题意,得
Y+x=180且x=y-30.
解得 x=75 ,y=105 .
所以∠ AOD = ∠ BOC =75 ° , ∠ DOE=1/2
∠ AOD=1/2×75 ° =37.5 ° ,
所以∠ COE =180 ° - ∠ DOE =180 °-37.5 ° =142.5 °
补充练习:
本节课你有何收获?
1.相交线,交点
2.对顶角的顶点相同,角的两边互为反向延长线
3.对顶角相等,邻补角互补.
归纳小结
①两条直线相交形成的角
②有一个公共顶点;
③没有公共边
①两条直线相交而成;
②有一个公共点;
③有一条公共边
对顶
角相
等
角的名称 特 征 性 质 相 同 点 不 同 点
对顶角
邻补角
邻补
角互
补
①都是两条直线相交而成的 角;
②都有一个公共顶点;
③都是成对出现的
①有无公共边
②两直线相交时,
对顶角只有一对
邻补角有两个
