分式的复习
图片预览










文档简介
(共35张PPT)
分式的概念、性质
分式方程及其应用
分式的乘除、加减
1.分式的定义:
2.分式有意义的条件:
B≠0
分式无意义的条件:
B = 0
3.分式值为 0 的条件:
A=0且 B ≠0
A
B
形如 ,其中 A ,B 都是整式,
且 B 中含有字母.
分式的概念
分式的概念及基本性质
分式的基本性质
分式的分子与分母同乘以(或除以)一个不为零的整式,分式的值不变。
用式子表示:
A
B
A X M
( )
A
B
A ÷ M
( )
=
=
分式的符号法则:
A
B
=
B
( )
=
A
( )
=
- A
( )
-A
-B
=
A
( )
=
B
( )
=
-A
( )
B X M
B÷M
-A
-B
-B
B
-A
B
分式的概念及基本性质
其中M为不为0的整式
分式的乘除法法则
分式乘分式
分式除以分式
分式的乘方
分式的加减
1.同分母分式相加减
2.异分母分式加减时需化为同分母分式加减.
这个相同的分母叫公分母.
(确定公分母的方法:一般取各分母系数的最小公倍数与各分母各个因式的最高次幂的积为公分母)
分式乘除及 加 减
2.当x= - 3 时,则分式
3.当 _________ 时,则分式 有意义
4.若分式 的值等于零,则应满
足的条件是
1.在代数式
中,分式共有_____个。
3
2
X=2
为常数
保证分母有意义
x≠3且x ≠-3
5、当x 时, 分式有意义。
6、写出下列各式中未知的分子或分母:
7、不改变分式的值,使下列分式的分子与分母的最高次项的系数是正数:
8、不改变分式的值,使下列各式分子与分母中各项的系数化为整数:
a2+ab
9.化简: = .
10.计算: = .
11.计算: = .
12.分式 的最简公分
母是_______________
1
14、 , 则
A=_____,B=____.
15、若关于x的方程 产生增根,
则m=______.
16、将公式 变形成用 表示 ,则
= 。
17.已知 ,那么分式 的值等于
________
18.已知 , 那么 = .
2
1
2
3
11
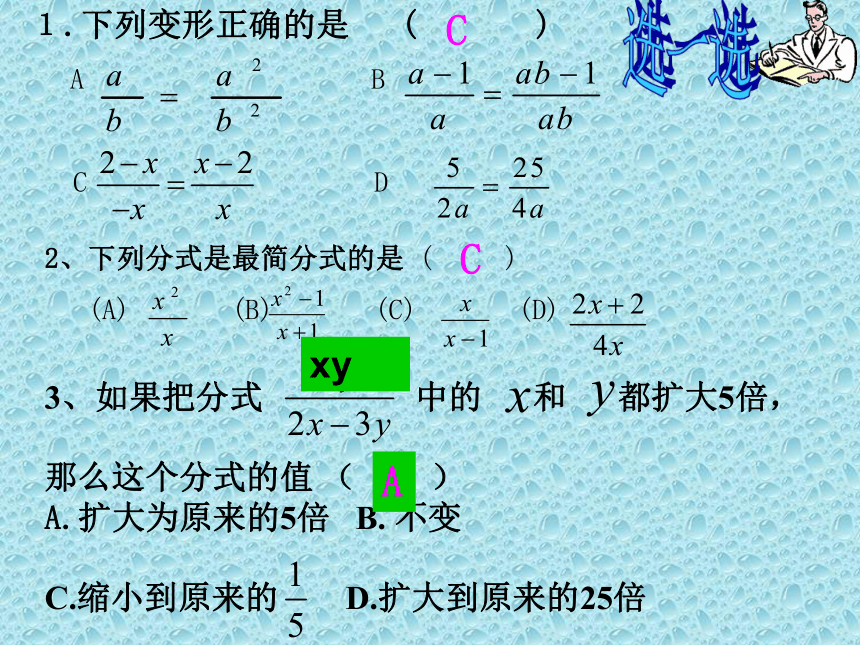
2、下列分式是最简分式的是 ( )
(A) (B) (C) (D)
C
C
1.下列变形正确的是 ( )
A B
C D
3、如果把分式 中的 和 都扩大5倍,
那么这个分式的值 ( )
A.扩大为原来的5倍 B. 不变
C.缩小到原来的 D.扩大到原来的25倍
xy
B
A
4、要使分式 有意义,则x的取值范围是
A、 B、
C、 且 D、 或
5、下列等式成立的是 ( )
A. B.
C. D.
6、下列各分式中,与 分式的值相等的是( )
A. B. C. D.
C
D
C
7. 如果公式 , 那么 b= ( )
A. B.
C. D.
8. 化简: =( )
A. 1 B.xy C. D.
C
C
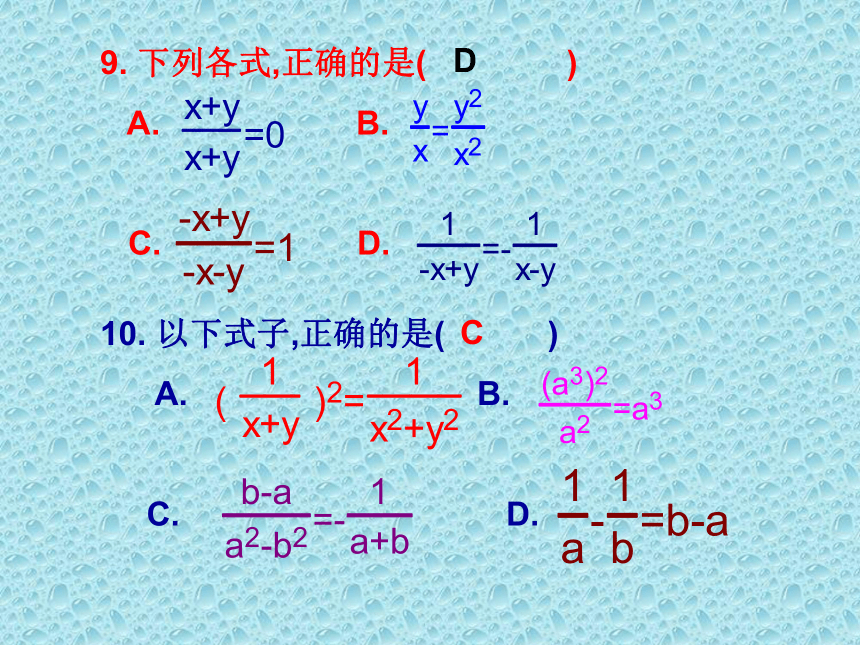
9. 下列各式,正确的是( )
A. B.
C. D.
10. 以下式子,正确的是( )
A. B.
C. D.
D
C
11. 化简 的结果是( )
A. B. C. D.
12. 化简 的结果是( )
A. B. C. D.
13. 下列各式中,正确的是( )
A. B.
C. D.
B
B
D
例3.请将下面的代数式尽可能化简,再选择一个你
喜欢的数代入求值
乘除为同级运算,运算顺序从左到右
错误!!!
例3.请将下面的代数式尽可能化简,再选择一个你
喜欢的数代入求值
a的取值保证分式有意义
1. 化简:
解:原式=
2. 化简:
解:原式
3. 计算:
4. 先化简,再求值:
÷
其中a满足
a-1
a+2
·
a
2
-4
a
2
-2a+1
1
a
2
-1
5. 有一道题“先化简,再求值:
,其中x=-3” 。小玲做题时
把“x=-3”错抄成了“x=3”,但她的计算结果也是正确的,请你解释这是怎么回事?
÷
7. 先化简 ÷
然后对a取一个你喜欢的数代入求值.
8. 先化简 代数式 ÷
然后选取一个使原式有意义的a值代入求值.
9. 对于试题:“先化简,再求值: ,其中x=2”.
某同学写出了如下解答:
解:
=x-3-(x+1)
=x-3+x+1=2x-2,
当x=2时,原式=2×2-2=2.
她的解答正确吗 如不正确,请你写出正确解答.
分式复习2
2.解分式方程的一般步骤
1、 在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2、解这个整式方程.
3、 把整式方程的根代入最简公分母,看结果是不是为零,使最简公分母为零的根是原方程的增根,必须舍去.
4、写出原方程的根.
1.解分式方程的思路是:
分式方程
整式方程
去分母
复习回顾一:
1、解方程:
解:原方程可化为
两边都乘以
,并整理得;
解得
检验:x=1是原方程的根,x=2是增根
∴原方程的根是x=1
例1
例2 已知
求A、B
解方程:
无解
5.若方程 有增根,则增根应是
6.解关于x的方程 产生增根,则常数a= 。
列分式方程解应用题的一般步骤
1.审:分析题意,找出研究对象,建立等量关系.
2.设:选择恰当的未知数,注意单位.
3.列:根据等量关系正确列出方程.
4.解:认真仔细.
5.验:不要忘记检验.
6.答:不要忘记写.
复习回顾二:
例1: 一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成, 问规定日期是几天?
解:设规定日期为x天,根据题意列方程
请完成下面的过程
例2. 已知轮船在静水中每小时行20千米,如果此船在某江中顺流航行72千米所用的时间与逆流航行48千米所用的时间相同,那么此江 水每小时的流速是多少千米
解:设江水每小时的流速是x千米,根据题意列方程
请完成下面的过程
例3.某人骑自行车比步行每小时多走8千米, 如果他步行12千米所用时间与骑车行36千米所用的时间相等,求他步行40千米用多少小时
解:设他步行1千米用x小时,根据题意列方程
请完成下面的过程
1.水池装有两个进水管,单独开甲管需a小时注满空池,单独开乙管需b小时注满空池,若同时打开两管,那么注满空池的时间是( )小时
A、 B、 C、 D、
2.A地在河的上游,B地在河的下游,若船从A地开往B地的速度为V1,从B地返回A地的速度为V2,则A、B两地间往返一次的平均速度为____
A、 B、 C D、无法计算
学以致用
例1 甲乙两人分别从相距36千米的A、B两地相向而行,
甲从A出发到1千米时发现有东西遗忘在A地,立即返回,
取过东西后又立即从A向B行进,这样两人恰好在AB中点
处相遇。已知甲比乙每小时多走0.5千米,求二人的速度
各是多少?
分析:等量关系 t 甲 = t 乙
36千米
1千米
A
B
路程
速度
时间
甲
乙
x
18
阿姨,我买些梨.
从这段对话里得出哪些信息或等量关系?
是小红啊! 你上次买的那种梨都卖完了,我们还没来
得及进货,我建议你这次买些新进的苹果,不过价格
要比梨贵一点,每千克苹果的价格是梨的1.5倍.
好吧,这次照上次一样,也花30元钱.
哟,巧了!这次苹果的质量正好比上次梨的质量轻2.5千克.
对啊,我本来就想要考考你,你能算出我这里的梨和苹果
的单价么
- - - 过了一会儿,苹果称好了 - - -
例2.请看下面一段对话:
请同学们帮帮小红吧!
小 红:
售货员:
小 红:
小 红:
售货员:
拓 展 题
从这段对话里得出哪些信息或等量关系?
例3、“东方大厦”进货员在苏州发现一种应季衬衫,预料能畅销嘉善市场,就用80000元购进所有衬衫,还急需2倍这种衬衫,经人介绍又在上海用176000元购进所需衬衫,只是单价比苏州贵4元.商厦按每件58元销售,销路很好,最后剩下的150件按八折销售,很快销售完,问商厦这笔生意盈利多少元
分式的概念、性质
分式方程及其应用
分式的乘除、加减
1.分式的定义:
2.分式有意义的条件:
B≠0
分式无意义的条件:
B = 0
3.分式值为 0 的条件:
A=0且 B ≠0
A
B
形如 ,其中 A ,B 都是整式,
且 B 中含有字母.
分式的概念
分式的概念及基本性质
分式的基本性质
分式的分子与分母同乘以(或除以)一个不为零的整式,分式的值不变。
用式子表示:
A
B
A X M
( )
A
B
A ÷ M
( )
=
=
分式的符号法则:
A
B
=
B
( )
=
A
( )
=
- A
( )
-A
-B
=
A
( )
=
B
( )
=
-A
( )
B X M
B÷M
-A
-B
-B
B
-A
B
分式的概念及基本性质
其中M为不为0的整式
分式的乘除法法则
分式乘分式
分式除以分式
分式的乘方
分式的加减
1.同分母分式相加减
2.异分母分式加减时需化为同分母分式加减.
这个相同的分母叫公分母.
(确定公分母的方法:一般取各分母系数的最小公倍数与各分母各个因式的最高次幂的积为公分母)
分式乘除及 加 减
2.当x= - 3 时,则分式
3.当 _________ 时,则分式 有意义
4.若分式 的值等于零,则应满
足的条件是
1.在代数式
中,分式共有_____个。
3
2
X=2
为常数
保证分母有意义
x≠3且x ≠-3
5、当x 时, 分式有意义。
6、写出下列各式中未知的分子或分母:
7、不改变分式的值,使下列分式的分子与分母的最高次项的系数是正数:
8、不改变分式的值,使下列各式分子与分母中各项的系数化为整数:
a2+ab
9.化简: = .
10.计算: = .
11.计算: = .
12.分式 的最简公分
母是_______________
1
14、 , 则
A=_____,B=____.
15、若关于x的方程 产生增根,
则m=______.
16、将公式 变形成用 表示 ,则
= 。
17.已知 ,那么分式 的值等于
________
18.已知 , 那么 = .
2
1
2
3
11
2、下列分式是最简分式的是 ( )
(A) (B) (C) (D)
C
C
1.下列变形正确的是 ( )
A B
C D
3、如果把分式 中的 和 都扩大5倍,
那么这个分式的值 ( )
A.扩大为原来的5倍 B. 不变
C.缩小到原来的 D.扩大到原来的25倍
xy
B
A
4、要使分式 有意义,则x的取值范围是
A、 B、
C、 且 D、 或
5、下列等式成立的是 ( )
A. B.
C. D.
6、下列各分式中,与 分式的值相等的是( )
A. B. C. D.
C
D
C
7. 如果公式 , 那么 b= ( )
A. B.
C. D.
8. 化简: =( )
A. 1 B.xy C. D.
C
C
9. 下列各式,正确的是( )
A. B.
C. D.
10. 以下式子,正确的是( )
A. B.
C. D.
D
C
11. 化简 的结果是( )
A. B. C. D.
12. 化简 的结果是( )
A. B. C. D.
13. 下列各式中,正确的是( )
A. B.
C. D.
B
B
D
例3.请将下面的代数式尽可能化简,再选择一个你
喜欢的数代入求值
乘除为同级运算,运算顺序从左到右
错误!!!
例3.请将下面的代数式尽可能化简,再选择一个你
喜欢的数代入求值
a的取值保证分式有意义
1. 化简:
解:原式=
2. 化简:
解:原式
3. 计算:
4. 先化简,再求值:
÷
其中a满足
a-1
a+2
·
a
2
-4
a
2
-2a+1
1
a
2
-1
5. 有一道题“先化简,再求值:
,其中x=-3” 。小玲做题时
把“x=-3”错抄成了“x=3”,但她的计算结果也是正确的,请你解释这是怎么回事?
÷
7. 先化简 ÷
然后对a取一个你喜欢的数代入求值.
8. 先化简 代数式 ÷
然后选取一个使原式有意义的a值代入求值.
9. 对于试题:“先化简,再求值: ,其中x=2”.
某同学写出了如下解答:
解:
=x-3-(x+1)
=x-3+x+1=2x-2,
当x=2时,原式=2×2-2=2.
她的解答正确吗 如不正确,请你写出正确解答.
分式复习2
2.解分式方程的一般步骤
1、 在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2、解这个整式方程.
3、 把整式方程的根代入最简公分母,看结果是不是为零,使最简公分母为零的根是原方程的增根,必须舍去.
4、写出原方程的根.
1.解分式方程的思路是:
分式方程
整式方程
去分母
复习回顾一:
1、解方程:
解:原方程可化为
两边都乘以
,并整理得;
解得
检验:x=1是原方程的根,x=2是增根
∴原方程的根是x=1
例1
例2 已知
求A、B
解方程:
无解
5.若方程 有增根,则增根应是
6.解关于x的方程 产生增根,则常数a= 。
列分式方程解应用题的一般步骤
1.审:分析题意,找出研究对象,建立等量关系.
2.设:选择恰当的未知数,注意单位.
3.列:根据等量关系正确列出方程.
4.解:认真仔细.
5.验:不要忘记检验.
6.答:不要忘记写.
复习回顾二:
例1: 一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成, 问规定日期是几天?
解:设规定日期为x天,根据题意列方程
请完成下面的过程
例2. 已知轮船在静水中每小时行20千米,如果此船在某江中顺流航行72千米所用的时间与逆流航行48千米所用的时间相同,那么此江 水每小时的流速是多少千米
解:设江水每小时的流速是x千米,根据题意列方程
请完成下面的过程
例3.某人骑自行车比步行每小时多走8千米, 如果他步行12千米所用时间与骑车行36千米所用的时间相等,求他步行40千米用多少小时
解:设他步行1千米用x小时,根据题意列方程
请完成下面的过程
1.水池装有两个进水管,单独开甲管需a小时注满空池,单独开乙管需b小时注满空池,若同时打开两管,那么注满空池的时间是( )小时
A、 B、 C、 D、
2.A地在河的上游,B地在河的下游,若船从A地开往B地的速度为V1,从B地返回A地的速度为V2,则A、B两地间往返一次的平均速度为____
A、 B、 C D、无法计算
学以致用
例1 甲乙两人分别从相距36千米的A、B两地相向而行,
甲从A出发到1千米时发现有东西遗忘在A地,立即返回,
取过东西后又立即从A向B行进,这样两人恰好在AB中点
处相遇。已知甲比乙每小时多走0.5千米,求二人的速度
各是多少?
分析:等量关系 t 甲 = t 乙
36千米
1千米
A
B
路程
速度
时间
甲
乙
x
18
阿姨,我买些梨.
从这段对话里得出哪些信息或等量关系?
是小红啊! 你上次买的那种梨都卖完了,我们还没来
得及进货,我建议你这次买些新进的苹果,不过价格
要比梨贵一点,每千克苹果的价格是梨的1.5倍.
好吧,这次照上次一样,也花30元钱.
哟,巧了!这次苹果的质量正好比上次梨的质量轻2.5千克.
对啊,我本来就想要考考你,你能算出我这里的梨和苹果
的单价么
- - - 过了一会儿,苹果称好了 - - -
例2.请看下面一段对话:
请同学们帮帮小红吧!
小 红:
售货员:
小 红:
小 红:
售货员:
拓 展 题
从这段对话里得出哪些信息或等量关系?
例3、“东方大厦”进货员在苏州发现一种应季衬衫,预料能畅销嘉善市场,就用80000元购进所有衬衫,还急需2倍这种衬衫,经人介绍又在上海用176000元购进所需衬衫,只是单价比苏州贵4元.商厦按每件58元销售,销路很好,最后剩下的150件按八折销售,很快销售完,问商厦这笔生意盈利多少元
