2020-2021学年安徽省亳州市涡阳县九年级(上)第一次联考数学试卷(word解析版)
文档属性
| 名称 | 2020-2021学年安徽省亳州市涡阳县九年级(上)第一次联考数学试卷(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 00:00:00 | ||
图片预览




文档简介
2020-2021学年安徽省亳州市涡阳县九年级(上)第一次联考数学试卷
一、选择题(共10小题,每小题4分,共40分)
1.(4分)在0,,,2,这五个数中,最小的数是
A.
B.
C.0
D.2
2.(4分)抛物线的顶点坐标是
A.
B.
C.
D.
3.(4分)如图,在中,,,则
A.
B.
C.
D.
4.(4分)已知点,,,都在反比例函数的图象上,则下列关系式一定正确的是
A.
B.
C.
D.
5.(4分)已知二次函数与轴有交点,则的取值范围是
A.
B.
C.且
D.且
6.(4分)如图,在正方形网格中,已知的三个顶点均在格点上,则的正弦值为
A.2
B.
C.
D.
7.(4分)已知:如图,,与交于点,,则
A.
B.
C.
D.
8.(4分)若抛物线与轴两个交点之间的距离为10,且,则关于的方程的根为
A.,
B.,
C.,
D.,
9.(4分)如图所示,抛物线的对称轴为直线.下列结论中:①;②;③;④.正确的结论是
A.①②
B.①④
C.①③④
D.①②④
10.(4分)如图,在边长为2的正方形中剪去一个边长为1的小正方形,动点从点出发,沿的路线绕多边形的边匀速运动到点时停止(不含点和点,则的面积随着时间变化的函数图象大致是
A.
B.
C.
D.
二、填空题(共4小题,每小题5分,共20分)
11.(5分)分解因式: .
12.(5分)用一根长的铁丝围成一个矩形,则矩形的最大面积为
.
13.(5分)如图,利用标杆测量树的高度,标杆的长是2.4米,若,米,则树高是
米.
14.(5分)将二次函数在轴上方的图象沿轴翻折到轴下方,图象的其余部分不变,得到一个新图象.若直线与这个新图象有3个公共点,则的值为
.
三、解答题(共2小题,每小题8分,共16分)
15.(8分)计算:
16.(8分)如图,在边长为1个单位长度的小正方形网格中.
(1)画出向上平移6个单位长度,再向右平移5个单位长度后的△.
(2)以点为位似中心,将放大为原来的2倍,得到△,请在网格中画出△.
四、解答题(共2小题,每小题8分,共16分)
17.(8分)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点和点.
(1)求反比例函数的关系式和点的坐标;
(2)结合图象,请直接写出在第一象限内,当时的取值范围.
18.(8分)阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为,依此类推,排在第位的数称为第项,记为.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母表示,如:数列1,3,9,27,为等比数列,其中,公比为.则:
(1)等比数列2,4,8,的公比为 ,第4项是 .
(2)如果一个数列,,,是等比数列,且公比为,那么根据定义可得到:
所以:,,.
由此可得: (用和的代数式表示).
(3)若一等比数列的公比,第2项是10,请求它的第1项与第5项.
五、解答题(共2小题,每小题10分,共20分)
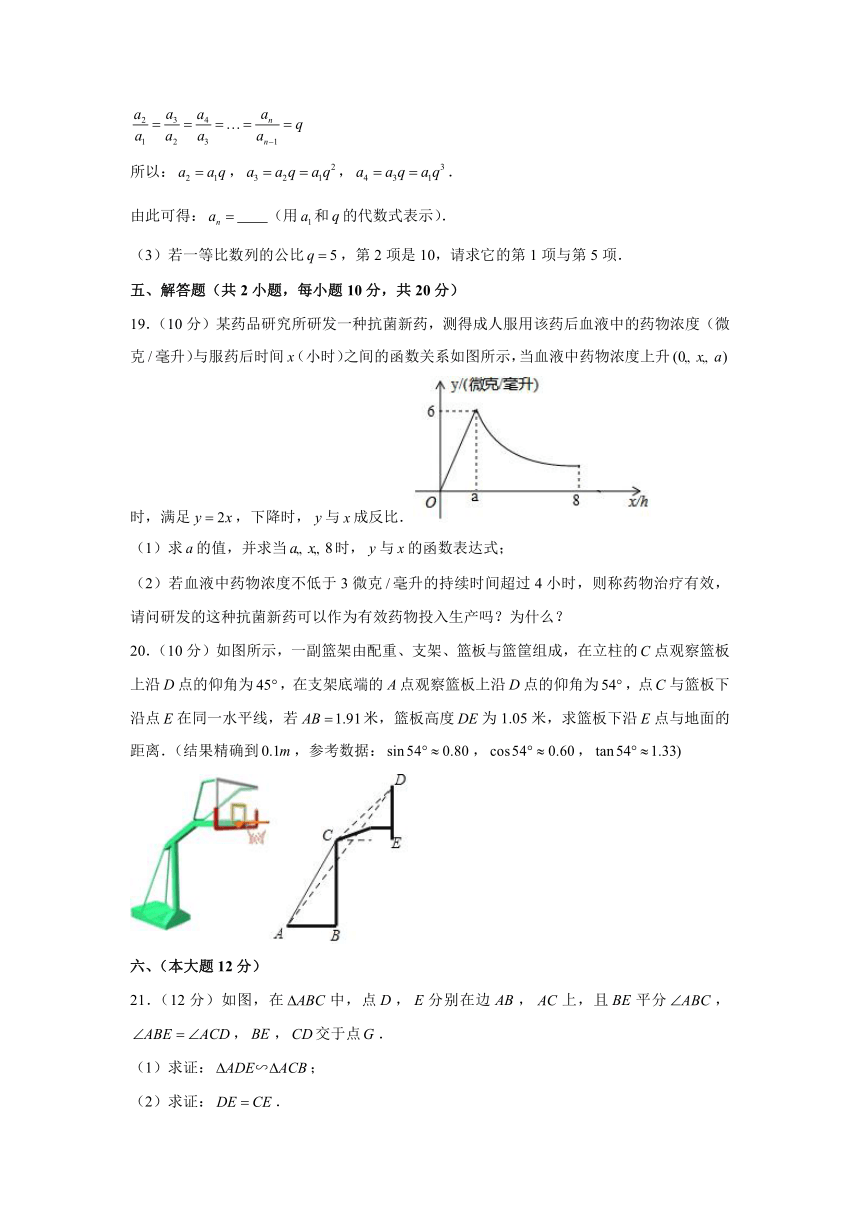
19.(10分)某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克毫升)与服药后时间(小时)之间的函数关系如图所示,当血液中药物浓度上升时,满足,下降时,与成反比.
(1)求的值,并求当时,与的函数表达式;
(2)若血液中药物浓度不低于3微克毫升的持续时间超过4小时,则称药物治疗有效,请问研发的这种抗菌新药可以作为有效药物投入生产吗?为什么?
20.(10分)如图所示,一副篮架由配重、支架、篮板与篮筐组成,在立柱的点观察篮板上沿点的仰角为,在支架底端的点观察篮板上沿点的仰角为,点与篮板下沿点在同一水平线,若米,篮板高度为1.05米,求篮板下沿点与地面的距离.(结果精确到,参考数据:,,
六、(本大题12分)
21.(12分)如图,在中,点,分别在边,上,且平分,,,交于点.
(1)求证:;
(2)求证:.
七、(本大题12分)
22.(12分)如图,在平面直角坐标系中,二次函数的图象经过点,点,与轴交于点.
(1)求,的值;
(2)若点为直线上一点,点到,两点的距离相等,将该抛物线向左(或向右)平移,得到一条新抛物线,并且新抛物线经过点,求新抛物线的顶点坐标.
八、(本大题14分)
23.(14分)如图1,在正方形中,点是上一点(不与,两点重合),连接,过点作于点,交对角线于点,交边于点,连接.
(1)求证:;
(2)如图2,若点是的中点,当时,求线段的长;
(3)设正方形的面积为,四边形的面积为,当时,值为
.(直接写答案)
参考答案与试题解析
一、选择题(共10小题,每小题4分,共40分)
1.(4分)在0,,,2,这五个数中,最小的数是
A.
B.
C.0
D.2
【分析】有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.
【解答】解:,,,
,
即最小的数是.
故选:.
2.(4分)抛物线的顶点坐标是
A.
B.
C.
D.
【分析】根据题目中二次函数的顶点式可以直接写出它的顶点坐标.
【解答】解:,
此函数的顶点坐标为,
故选:.
3.(4分)如图,在中,,,则
A.
B.
C.
D.
【分析】平行于三角形一边的直线截其他两边,所得的对应线段成比例,列出比例式即可得到所求的比值.
【解答】解:,
,
又,
,
故选:.
4.(4分)已知点,,,都在反比例函数的图象上,则下列关系式一定正确的是
A.
B.
C.
D.
【分析】利用反比例函数图象上点的坐标特征求出与,然后对各选项进行判断.
【解答】解:点,,,都在反比例函数的图象上,
,,
,,
.
故选:.
5.(4分)已知二次函数与轴有交点,则的取值范围是
A.
B.
C.且
D.且
【分析】根据题意可以得到关于的不等式组,从而可以求得的取值范围,注意二次项系数.
【解答】解:二次函数与轴有交点,
,
解得,且,
即的取值范围是且,
故选:.
6.(4分)如图,在正方形网格中,已知的三个顶点均在格点上,则的正弦值为
A.2
B.
C.
D.
【分析】延长交网格于,连接,则,由勾股定理得出,,由三角函数定义即可得出答案.
【解答】解:延长交网格于,连接,如图所示:
则,
,,
的正弦值;
故选:.
7.(4分)已知:如图,,与交于点,,则
A.
B.
C.
D.
【分析】由,与交于点,,可得,,又三角形的面积比等于相似比的平方可得结论.
【解答】解:如图,,与交于点,,
,且,
.
故选:.
8.(4分)若抛物线与轴两个交点之间的距离为10,且,则关于的方程的根为
A.,
B.,
C.,
D.,
【分析】函数的对称轴为,即可求解.
【解答】解:函数的对称轴为,
而两个交点之间的距离为10,
则两个交点的坐标分别为:、,
故选:.
9.(4分)如图所示,抛物线的对称轴为直线.下列结论中:①;②;③;④.正确的结论是
A.①②
B.①④
C.①③④
D.①②④
【分析】依据函数的图象和性质逐个求解即可.
【解答】解:①函数的对称轴在轴右侧,则,而,故,正确,符合题意;
②从图象看,当时,,即,故②正确,符合题意;
③从图象看,抛物线与轴由两个交点,故,故③错误,不符合题意;
④抛物线的对称轴,则.
抛物线与轴交点的纵坐标是2,即.
如图所示,当时,,即,
即,故④正确,符合题意;
故选:.
10.(4分)如图,在边长为2的正方形中剪去一个边长为1的小正方形,动点从点出发,沿的路线绕多边形的边匀速运动到点时停止(不含点和点,则的面积随着时间变化的函数图象大致是
A.
B.
C.
D.
【分析】分析动点在每段路径上的运动的过程中的面积增大、减小或不变的趋势即可.
【解答】解:由点的运动可知,当点在、边上时的面积不变,则对应图象为平行于轴的线段,则、错误.点在、、上运动时,的面积分别处于增、减变化过程.故排除
故选:.
二、填空题(共4小题,每小题5分,共20分)
11.(5分)分解因式: .
【分析】原式提取,再利用平方差公式分解即可.
【解答】解:原式
.
故答案为:
12.(5分)用一根长的铁丝围成一个矩形,则矩形的最大面积为
225 .
【分析】先设出矩形的长,即可得到宽,然后即可表示表示出面积,再化为二次函数的顶点式,即可求得该矩形的最大面积.
【解答】解:设矩形的长为,则宽为,面积为,
,
该函数图象开口向下,当时,该函数取得最大值225,
故答案为:225.
13.(5分)如图,利用标杆测量树的高度,标杆的长是2.4米,若,米,则树高是
15 米.
【分析】在中求出,再在中求出即可.
【解答】解:在中,,米,,
,
(米,
(米,
在中,,
,
(米,
故答案为:15.
14.(5分)将二次函数在轴上方的图象沿轴翻折到轴下方,图象的其余部分不变,得到一个新图象.若直线与这个新图象有3个公共点,则的值为
或 .
【分析】如图所示,过点作直线,将直线向下平移到恰好相切位置,根据一次函数在这两个位置时,两个图象恰好有3个交点,即可求的值.
【解答】解:如图所示,直线、在图示位置时,直线与新图象有3个交点,
,令,则或,则点,
将点的坐标代入即可解得:,
二次函数在轴下方的图象对应的函数表达式为:,
令,
整理得:,
△,解得:,
故答案为:或.
三、解答题(共2小题,每小题8分,共16分)
15.(8分)计算:
【分析】直接利用特殊角的三角函数值以及二次根式的性质分别化简得出答案.
【解答】解:
.
16.(8分)如图,在边长为1个单位长度的小正方形网格中.
(1)画出向上平移6个单位长度,再向右平移5个单位长度后的△.
(2)以点为位似中心,将放大为原来的2倍,得到△,请在网格中画出△.
【分析】(1)将向上平移6个单位长度,再向右平移5个单位长度后的△,如图所示;
(2)以点为位似中心,将放大为原来的2倍,得到△,如图所示.
【解答】解:(1)根据题意画出图形,△为所求三角形;
(2)根据题意画出图形,△为所求三角形.
四、解答题(共2小题,每小题8分,共16分)
17.(8分)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点和点.
(1)求反比例函数的关系式和点的坐标;
(2)结合图象,请直接写出在第一象限内,当时的取值范围.
【分析】(1)把点代入,求得的值,然后根据待定系数法即可求得反比例函数的关系式,解析式联立成方程组,解方程组求得点的坐标;
(2)根据图象即可求得.
【解答】解:(1)在一次函数的图象上,
,
,
反比例函数的图象经过点,
,
反比例函数的解析式为,
解得或,
的坐标为;
(2)由图象可知,在第一象限内,当时的取值范围是.
18.(8分)阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为,依此类推,排在第位的数称为第项,记为.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母表示,如:数列1,3,9,27,为等比数列,其中,公比为.则:
(1)等比数列2,4,8,的公比为 2 ,第4项是 .
(2)如果一个数列,,,是等比数列,且公比为,那么根据定义可得到:
所以:,,.
由此可得: (用和的代数式表示).
(3)若一等比数列的公比,第2项是10,请求它的第1项与第5项.
【分析】(1)由第二项除以第一项求出公比的值,确定出第4项即可;
(2)根据题中的定义归纳总结得到通项公式即可;
(3)由公比与第二项的值求出第一项的值,进而确定出第5项的值.
【解答】解:(1),第4项是16;
(2)归纳总结得:;
(3)等比数列的公比,第二项为10,
,.
故答案为:(1)2;16;(2).
五、解答题(共2小题,每小题10分,共20分)
19.(10分)某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克毫升)与服药后时间(小时)之间的函数关系如图所示,当血液中药物浓度上升时,满足,下降时,与成反比.
(1)求的值,并求当时,与的函数表达式;
(2)若血液中药物浓度不低于3微克毫升的持续时间超过4小时,则称药物治疗有效,请问研发的这种抗菌新药可以作为有效药物投入生产吗?为什么?
【分析】(1)分别利用正比例函数以及反比例函数解析式求法得出即可;
(2)把分别代入正比例函数和反比例函数解析式求出自变量的值,进而得出答案.
【解答】解:(1)有图象知,;
又由题意可知:当时,与成反比,设.
由图象可知,当时,,
;
;
(2)把分别代入和得,和,
,
抗菌新药可以作为有效药物投入生产.
20.(10分)如图所示,一副篮架由配重、支架、篮板与篮筐组成,在立柱的点观察篮板上沿点的仰角为,在支架底端的点观察篮板上沿点的仰角为,点与篮板下沿点在同一水平线,若米,篮板高度为1.05米,求篮板下沿点与地面的距离.(结果精确到,参考数据:,,
【分析】延长与的延长线交于点,则四边形是矩形,可得,,根据题意可得,,,再根据锐角三角函数即可求出篮板下沿点与地面的距离.
【解答】解:如图,
延长与的延长线交于点,
则四边形是矩形,
,,
根据题意可知:
,
,
在中,,
,
,
,
即,
解得(米.
答:篮板下沿点与地面的距离约为2.9米.
六、(本大题12分)
21.(12分)如图,在中,点,分别在边,上,且平分,,,交于点.
(1)求证:;
(2)求证:.
【分析】(1)由题可知,所以,即,又,所以;
(2)由(1)知,结合三角形外角的性质定理及平分线的性质可得,可得结论.
【解答】证明:(1)如图,,,
,
,
,
又,
;
(2)由(1)知,,
,
,,
,
,
,
平分,
,
,
.
七、(本大题12分)
22.(12分)如图,在平面直角坐标系中,二次函数的图象经过点,点,与轴交于点.
(1)求,的值;
(2)若点为直线上一点,点到,两点的距离相等,将该抛物线向左(或向右)平移,得到一条新抛物线,并且新抛物线经过点,求新抛物线的顶点坐标.
【分析】(1)利用待定系数法即可求得;
(2)求得直线的解析式,根据题意点在抛物线的对称轴上,从而求得的坐标,设平移后的新抛物线的解析式为,代入的坐标,求得的值,从而求得顶点坐标.
【解答】解:(1)二次函数的图象经过点,点,
,解得;
(2),
抛物线的对称轴为直线,,
点到,两点的距离相等,
点在抛物线的对称轴上,
,,
直线的解析式为,
令,则,
,
设平移后的新抛物线的解析式为,
新抛物线经过点,
,
解得,,
新抛物线的顶点坐标为,或,.
八、(本大题14分)
23.(14分)如图1,在正方形中,点是上一点(不与,两点重合),连接,过点作于点,交对角线于点,交边于点,连接.
(1)求证:;
(2)如图2,若点是的中点,当时,求线段的长;
(3)设正方形的面积为,四边形的面积为,当时,值为
.(直接写答案)
【分析】(1)可得,根据可证明,即可求解;
(2)由,及,可得,则,可求出的长;
(3)设,则,,求出和即可得出答案.
【解答】(1)证明:四边形是正方形,
,,
,
,
,
,
,
在和中,
,
,
;
(2)解:,
,,
点是的中点,
,
,
,
,
,
,
设,则,
,
即;
(3)解:当的值为时,则,
,,
,
,
,
,,
设,则,,
,
,
,
,
,
,
故答案为:.
一、选择题(共10小题,每小题4分,共40分)
1.(4分)在0,,,2,这五个数中,最小的数是
A.
B.
C.0
D.2
2.(4分)抛物线的顶点坐标是
A.
B.
C.
D.
3.(4分)如图,在中,,,则
A.
B.
C.
D.
4.(4分)已知点,,,都在反比例函数的图象上,则下列关系式一定正确的是
A.
B.
C.
D.
5.(4分)已知二次函数与轴有交点,则的取值范围是
A.
B.
C.且
D.且
6.(4分)如图,在正方形网格中,已知的三个顶点均在格点上,则的正弦值为
A.2
B.
C.
D.
7.(4分)已知:如图,,与交于点,,则
A.
B.
C.
D.
8.(4分)若抛物线与轴两个交点之间的距离为10,且,则关于的方程的根为
A.,
B.,
C.,
D.,
9.(4分)如图所示,抛物线的对称轴为直线.下列结论中:①;②;③;④.正确的结论是
A.①②
B.①④
C.①③④
D.①②④
10.(4分)如图,在边长为2的正方形中剪去一个边长为1的小正方形,动点从点出发,沿的路线绕多边形的边匀速运动到点时停止(不含点和点,则的面积随着时间变化的函数图象大致是
A.
B.
C.
D.
二、填空题(共4小题,每小题5分,共20分)
11.(5分)分解因式: .
12.(5分)用一根长的铁丝围成一个矩形,则矩形的最大面积为
.
13.(5分)如图,利用标杆测量树的高度,标杆的长是2.4米,若,米,则树高是
米.
14.(5分)将二次函数在轴上方的图象沿轴翻折到轴下方,图象的其余部分不变,得到一个新图象.若直线与这个新图象有3个公共点,则的值为
.
三、解答题(共2小题,每小题8分,共16分)
15.(8分)计算:
16.(8分)如图,在边长为1个单位长度的小正方形网格中.
(1)画出向上平移6个单位长度,再向右平移5个单位长度后的△.
(2)以点为位似中心,将放大为原来的2倍,得到△,请在网格中画出△.
四、解答题(共2小题,每小题8分,共16分)
17.(8分)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点和点.
(1)求反比例函数的关系式和点的坐标;
(2)结合图象,请直接写出在第一象限内,当时的取值范围.
18.(8分)阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为,依此类推,排在第位的数称为第项,记为.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母表示,如:数列1,3,9,27,为等比数列,其中,公比为.则:
(1)等比数列2,4,8,的公比为 ,第4项是 .
(2)如果一个数列,,,是等比数列,且公比为,那么根据定义可得到:
所以:,,.
由此可得: (用和的代数式表示).
(3)若一等比数列的公比,第2项是10,请求它的第1项与第5项.
五、解答题(共2小题,每小题10分,共20分)
19.(10分)某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克毫升)与服药后时间(小时)之间的函数关系如图所示,当血液中药物浓度上升时,满足,下降时,与成反比.
(1)求的值,并求当时,与的函数表达式;
(2)若血液中药物浓度不低于3微克毫升的持续时间超过4小时,则称药物治疗有效,请问研发的这种抗菌新药可以作为有效药物投入生产吗?为什么?
20.(10分)如图所示,一副篮架由配重、支架、篮板与篮筐组成,在立柱的点观察篮板上沿点的仰角为,在支架底端的点观察篮板上沿点的仰角为,点与篮板下沿点在同一水平线,若米,篮板高度为1.05米,求篮板下沿点与地面的距离.(结果精确到,参考数据:,,
六、(本大题12分)
21.(12分)如图,在中,点,分别在边,上,且平分,,,交于点.
(1)求证:;
(2)求证:.
七、(本大题12分)
22.(12分)如图,在平面直角坐标系中,二次函数的图象经过点,点,与轴交于点.
(1)求,的值;
(2)若点为直线上一点,点到,两点的距离相等,将该抛物线向左(或向右)平移,得到一条新抛物线,并且新抛物线经过点,求新抛物线的顶点坐标.
八、(本大题14分)
23.(14分)如图1,在正方形中,点是上一点(不与,两点重合),连接,过点作于点,交对角线于点,交边于点,连接.
(1)求证:;
(2)如图2,若点是的中点,当时,求线段的长;
(3)设正方形的面积为,四边形的面积为,当时,值为
.(直接写答案)
参考答案与试题解析
一、选择题(共10小题,每小题4分,共40分)
1.(4分)在0,,,2,这五个数中,最小的数是
A.
B.
C.0
D.2
【分析】有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.
【解答】解:,,,
,
即最小的数是.
故选:.
2.(4分)抛物线的顶点坐标是
A.
B.
C.
D.
【分析】根据题目中二次函数的顶点式可以直接写出它的顶点坐标.
【解答】解:,
此函数的顶点坐标为,
故选:.
3.(4分)如图,在中,,,则
A.
B.
C.
D.
【分析】平行于三角形一边的直线截其他两边,所得的对应线段成比例,列出比例式即可得到所求的比值.
【解答】解:,
,
又,
,
故选:.
4.(4分)已知点,,,都在反比例函数的图象上,则下列关系式一定正确的是
A.
B.
C.
D.
【分析】利用反比例函数图象上点的坐标特征求出与,然后对各选项进行判断.
【解答】解:点,,,都在反比例函数的图象上,
,,
,,
.
故选:.
5.(4分)已知二次函数与轴有交点,则的取值范围是
A.
B.
C.且
D.且
【分析】根据题意可以得到关于的不等式组,从而可以求得的取值范围,注意二次项系数.
【解答】解:二次函数与轴有交点,
,
解得,且,
即的取值范围是且,
故选:.
6.(4分)如图,在正方形网格中,已知的三个顶点均在格点上,则的正弦值为
A.2
B.
C.
D.
【分析】延长交网格于,连接,则,由勾股定理得出,,由三角函数定义即可得出答案.
【解答】解:延长交网格于,连接,如图所示:
则,
,,
的正弦值;
故选:.
7.(4分)已知:如图,,与交于点,,则
A.
B.
C.
D.
【分析】由,与交于点,,可得,,又三角形的面积比等于相似比的平方可得结论.
【解答】解:如图,,与交于点,,
,且,
.
故选:.
8.(4分)若抛物线与轴两个交点之间的距离为10,且,则关于的方程的根为
A.,
B.,
C.,
D.,
【分析】函数的对称轴为,即可求解.
【解答】解:函数的对称轴为,
而两个交点之间的距离为10,
则两个交点的坐标分别为:、,
故选:.
9.(4分)如图所示,抛物线的对称轴为直线.下列结论中:①;②;③;④.正确的结论是
A.①②
B.①④
C.①③④
D.①②④
【分析】依据函数的图象和性质逐个求解即可.
【解答】解:①函数的对称轴在轴右侧,则,而,故,正确,符合题意;
②从图象看,当时,,即,故②正确,符合题意;
③从图象看,抛物线与轴由两个交点,故,故③错误,不符合题意;
④抛物线的对称轴,则.
抛物线与轴交点的纵坐标是2,即.
如图所示,当时,,即,
即,故④正确,符合题意;
故选:.
10.(4分)如图,在边长为2的正方形中剪去一个边长为1的小正方形,动点从点出发,沿的路线绕多边形的边匀速运动到点时停止(不含点和点,则的面积随着时间变化的函数图象大致是
A.
B.
C.
D.
【分析】分析动点在每段路径上的运动的过程中的面积增大、减小或不变的趋势即可.
【解答】解:由点的运动可知,当点在、边上时的面积不变,则对应图象为平行于轴的线段,则、错误.点在、、上运动时,的面积分别处于增、减变化过程.故排除
故选:.
二、填空题(共4小题,每小题5分,共20分)
11.(5分)分解因式: .
【分析】原式提取,再利用平方差公式分解即可.
【解答】解:原式
.
故答案为:
12.(5分)用一根长的铁丝围成一个矩形,则矩形的最大面积为
225 .
【分析】先设出矩形的长,即可得到宽,然后即可表示表示出面积,再化为二次函数的顶点式,即可求得该矩形的最大面积.
【解答】解:设矩形的长为,则宽为,面积为,
,
该函数图象开口向下,当时,该函数取得最大值225,
故答案为:225.
13.(5分)如图,利用标杆测量树的高度,标杆的长是2.4米,若,米,则树高是
15 米.
【分析】在中求出,再在中求出即可.
【解答】解:在中,,米,,
,
(米,
(米,
在中,,
,
(米,
故答案为:15.
14.(5分)将二次函数在轴上方的图象沿轴翻折到轴下方,图象的其余部分不变,得到一个新图象.若直线与这个新图象有3个公共点,则的值为
或 .
【分析】如图所示,过点作直线,将直线向下平移到恰好相切位置,根据一次函数在这两个位置时,两个图象恰好有3个交点,即可求的值.
【解答】解:如图所示,直线、在图示位置时,直线与新图象有3个交点,
,令,则或,则点,
将点的坐标代入即可解得:,
二次函数在轴下方的图象对应的函数表达式为:,
令,
整理得:,
△,解得:,
故答案为:或.
三、解答题(共2小题,每小题8分,共16分)
15.(8分)计算:
【分析】直接利用特殊角的三角函数值以及二次根式的性质分别化简得出答案.
【解答】解:
.
16.(8分)如图,在边长为1个单位长度的小正方形网格中.
(1)画出向上平移6个单位长度,再向右平移5个单位长度后的△.
(2)以点为位似中心,将放大为原来的2倍,得到△,请在网格中画出△.
【分析】(1)将向上平移6个单位长度,再向右平移5个单位长度后的△,如图所示;
(2)以点为位似中心,将放大为原来的2倍,得到△,如图所示.
【解答】解:(1)根据题意画出图形,△为所求三角形;
(2)根据题意画出图形,△为所求三角形.
四、解答题(共2小题,每小题8分,共16分)
17.(8分)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点和点.
(1)求反比例函数的关系式和点的坐标;
(2)结合图象,请直接写出在第一象限内,当时的取值范围.
【分析】(1)把点代入,求得的值,然后根据待定系数法即可求得反比例函数的关系式,解析式联立成方程组,解方程组求得点的坐标;
(2)根据图象即可求得.
【解答】解:(1)在一次函数的图象上,
,
,
反比例函数的图象经过点,
,
反比例函数的解析式为,
解得或,
的坐标为;
(2)由图象可知,在第一象限内,当时的取值范围是.
18.(8分)阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为,依此类推,排在第位的数称为第项,记为.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母表示,如:数列1,3,9,27,为等比数列,其中,公比为.则:
(1)等比数列2,4,8,的公比为 2 ,第4项是 .
(2)如果一个数列,,,是等比数列,且公比为,那么根据定义可得到:
所以:,,.
由此可得: (用和的代数式表示).
(3)若一等比数列的公比,第2项是10,请求它的第1项与第5项.
【分析】(1)由第二项除以第一项求出公比的值,确定出第4项即可;
(2)根据题中的定义归纳总结得到通项公式即可;
(3)由公比与第二项的值求出第一项的值,进而确定出第5项的值.
【解答】解:(1),第4项是16;
(2)归纳总结得:;
(3)等比数列的公比,第二项为10,
,.
故答案为:(1)2;16;(2).
五、解答题(共2小题,每小题10分,共20分)
19.(10分)某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克毫升)与服药后时间(小时)之间的函数关系如图所示,当血液中药物浓度上升时,满足,下降时,与成反比.
(1)求的值,并求当时,与的函数表达式;
(2)若血液中药物浓度不低于3微克毫升的持续时间超过4小时,则称药物治疗有效,请问研发的这种抗菌新药可以作为有效药物投入生产吗?为什么?
【分析】(1)分别利用正比例函数以及反比例函数解析式求法得出即可;
(2)把分别代入正比例函数和反比例函数解析式求出自变量的值,进而得出答案.
【解答】解:(1)有图象知,;
又由题意可知:当时,与成反比,设.
由图象可知,当时,,
;
;
(2)把分别代入和得,和,
,
抗菌新药可以作为有效药物投入生产.
20.(10分)如图所示,一副篮架由配重、支架、篮板与篮筐组成,在立柱的点观察篮板上沿点的仰角为,在支架底端的点观察篮板上沿点的仰角为,点与篮板下沿点在同一水平线,若米,篮板高度为1.05米,求篮板下沿点与地面的距离.(结果精确到,参考数据:,,
【分析】延长与的延长线交于点,则四边形是矩形,可得,,根据题意可得,,,再根据锐角三角函数即可求出篮板下沿点与地面的距离.
【解答】解:如图,
延长与的延长线交于点,
则四边形是矩形,
,,
根据题意可知:
,
,
在中,,
,
,
,
即,
解得(米.
答:篮板下沿点与地面的距离约为2.9米.
六、(本大题12分)
21.(12分)如图,在中,点,分别在边,上,且平分,,,交于点.
(1)求证:;
(2)求证:.
【分析】(1)由题可知,所以,即,又,所以;
(2)由(1)知,结合三角形外角的性质定理及平分线的性质可得,可得结论.
【解答】证明:(1)如图,,,
,
,
,
又,
;
(2)由(1)知,,
,
,,
,
,
,
平分,
,
,
.
七、(本大题12分)
22.(12分)如图,在平面直角坐标系中,二次函数的图象经过点,点,与轴交于点.
(1)求,的值;
(2)若点为直线上一点,点到,两点的距离相等,将该抛物线向左(或向右)平移,得到一条新抛物线,并且新抛物线经过点,求新抛物线的顶点坐标.
【分析】(1)利用待定系数法即可求得;
(2)求得直线的解析式,根据题意点在抛物线的对称轴上,从而求得的坐标,设平移后的新抛物线的解析式为,代入的坐标,求得的值,从而求得顶点坐标.
【解答】解:(1)二次函数的图象经过点,点,
,解得;
(2),
抛物线的对称轴为直线,,
点到,两点的距离相等,
点在抛物线的对称轴上,
,,
直线的解析式为,
令,则,
,
设平移后的新抛物线的解析式为,
新抛物线经过点,
,
解得,,
新抛物线的顶点坐标为,或,.
八、(本大题14分)
23.(14分)如图1,在正方形中,点是上一点(不与,两点重合),连接,过点作于点,交对角线于点,交边于点,连接.
(1)求证:;
(2)如图2,若点是的中点,当时,求线段的长;
(3)设正方形的面积为,四边形的面积为,当时,值为
.(直接写答案)
【分析】(1)可得,根据可证明,即可求解;
(2)由,及,可得,则,可求出的长;
(3)设,则,,求出和即可得出答案.
【解答】(1)证明:四边形是正方形,
,,
,
,
,
,
,
在和中,
,
,
;
(2)解:,
,,
点是的中点,
,
,
,
,
,
,
设,则,
,
即;
(3)解:当的值为时,则,
,,
,
,
,
,,
设,则,,
,
,
,
,
,
,
故答案为:.
同课章节目录
