2021-2022学年八年级数学人教版上册12.2全等三角形的判定(三)ASA、AAS课件(18张ppt)
文档属性
| 名称 | 2021-2022学年八年级数学人教版上册12.2全等三角形的判定(三)ASA、AAS课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 313.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
12.2全等三角形的判定(三)
ASA
AAS
(2)
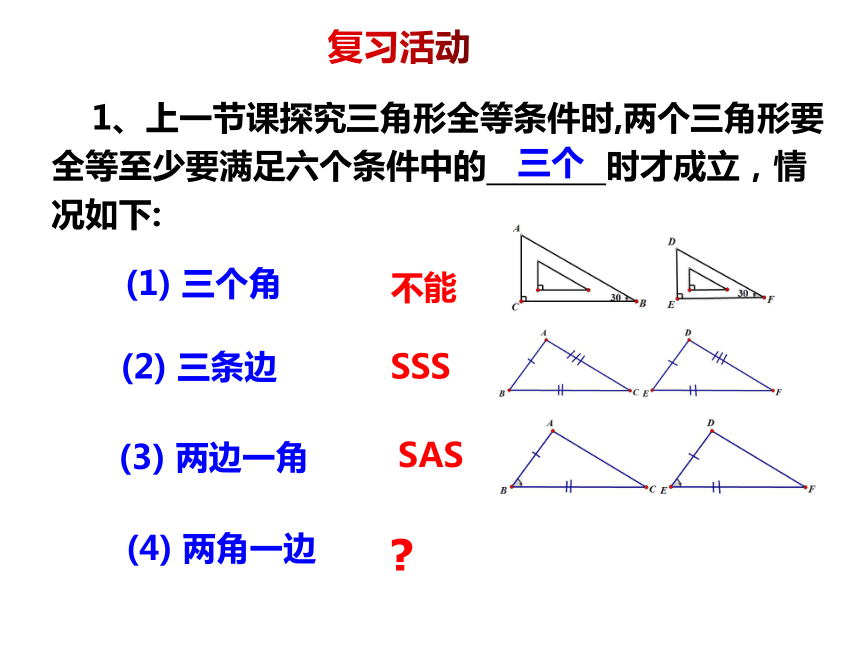
三条边
(1)
三个角
(3)
两边一角
(4)
两角一边
1、上一节课探究三角形全等条件时,两个三角形要全等至少要满足六个条件中的
时才成立,情况如下:
SSS
不能
?
SAS
三个
复习活动
A
B
C
A′
B′
C′
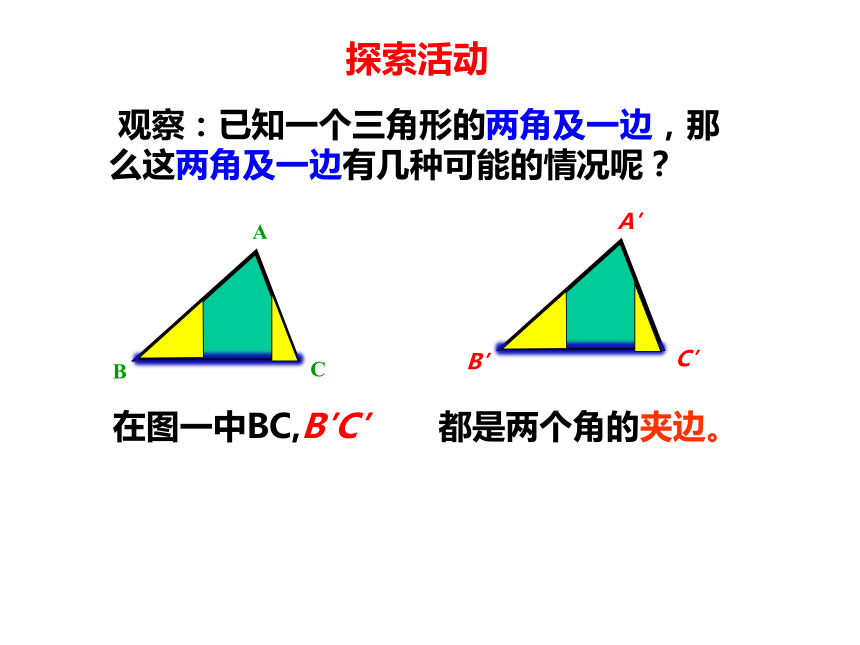
在图一中BC,B′C′
都是两个角的夹边。
观察:已知一个三角形的两角及一边,那么这两角及一边有几种可能的情况呢?
探索活动
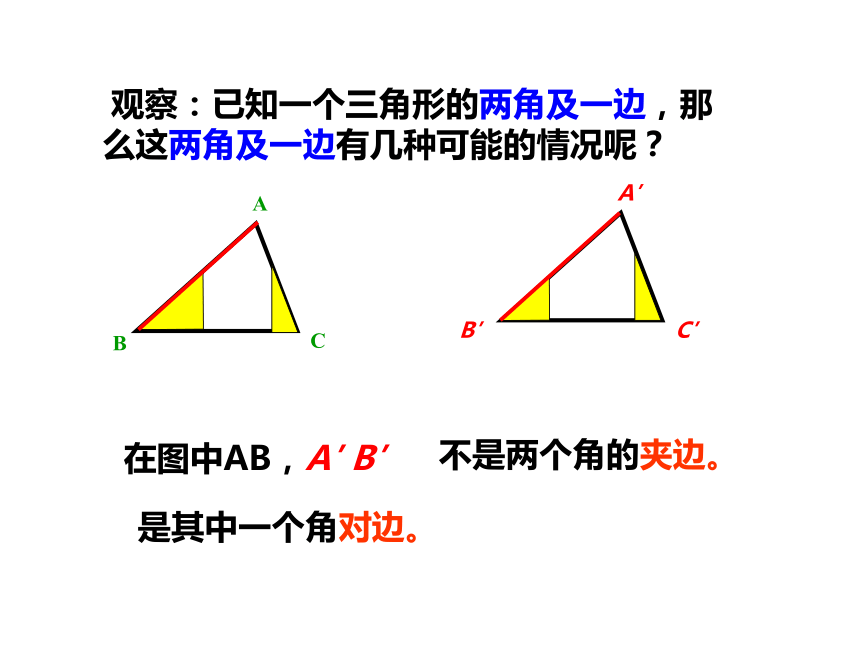
观察:已知一个三角形的两角及一边,那么这两角及一边有几种可能的情况呢?
A
B
C
A′
B′
C′
在图中AB,A′
B′
不是两个角的夹边。
是其中一个角对边。
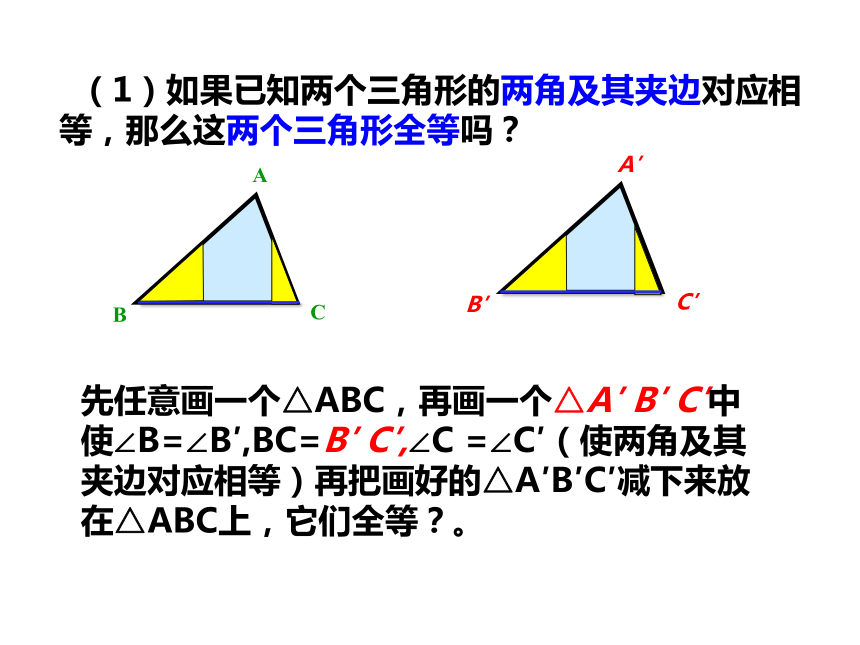
(1)如果已知两个三角形的两角及其夹边对应相等,那么这两个三角形全等吗?
A
B
C
A′
B′
C′
先任意画一个△ABC,再画一个△A′
B′
C′中使∠B=∠B′,BC=B′
C′,∠C
=∠C′(使两角及其夹边对应相等)再把画好的△A′B′C′减下来放在△ABC上,它们全等?。
画法:1、画B′
C′=BC;
2、在B′
C′
的同旁画∠DB′
C′=∠B
,
∠EC′B′
=∠C,
B′
D,C′
E交于点A′
。
B
A
C
B′
C′
A′
E
D
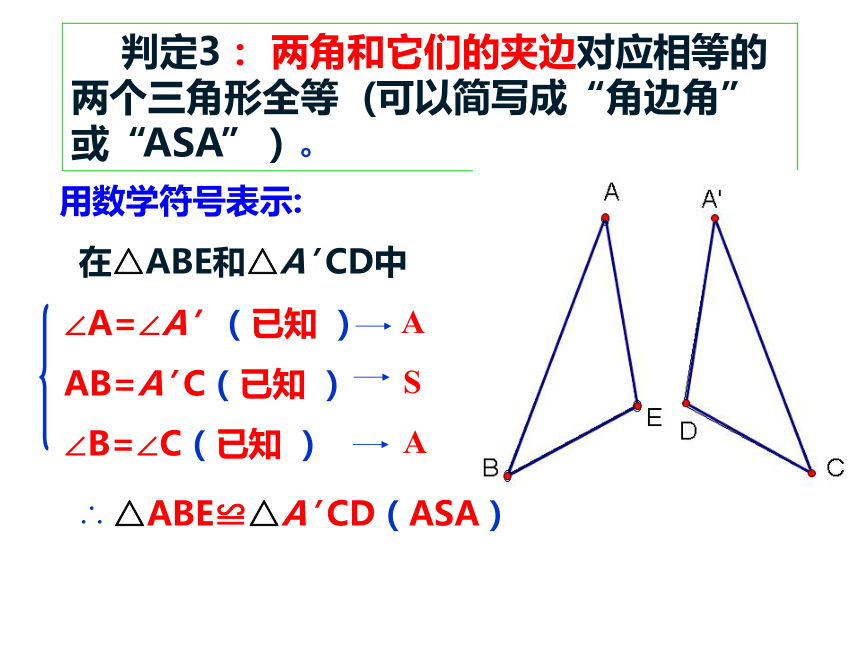
判定3:
两角和它们的夹边对应相等的两个三角形全等
(可以简写成“角边角”或“ASA”)。
∠A=∠A′
(已知
)
AB=A′
C(已知
)
∠B=∠C(已知
)
在△ABE和△A′
CD中
∴
△ABE≌△A′
CD(ASA)
A
S
A
用数学符号表示:
已知,在△ABE和△A′
CD中,AE=A′
D,∠A=∠A′
,∠B=∠C,求证△ABE≌△A′
CD
(2)两个角和其中一个角的对边对应相等的两个三角形全等吗?。
∠A=∠A′
(已知
)
∠B=∠C(已知
)
AE=A′
D(已知
)
在△ABE和△A′
CD中
∴
△ABE≌△A′
CD(AAS)
用数学符号表示:
判定4:两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)。
例1
已知:∠ABC=∠DCB,∠ACB=
∠DBC,
求证:
△
ABC
≌
△
DCB.
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
证明:
在ABC和△DCB中,
∴△ABC≌△DCB(ASA
).
B
C
A
D
巩固提升
例2.已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C。
求证:(1)AD=AE;
(2)BD=CE。
证明
:在△ADC和△AEB中
∠A=∠A(公共角)
AC=AB(已知)
∠C=∠B(已知)
∴△ACD≌△ABE(ASA)
∴AD=AE(全等三角形的对应边相等)
又∵AB=AC(已知)
∴BD=CE
小结:
到目前为止,我们一共探索出判定三角形全等的四种方法,它们分别是:
1、边边边
(SSS)
3、角边角
(ASA)
4、角角边
(AAS)
2、边角边
(SAS)
例3
如图,O是AB的中点,∠A=
∠B,
△
AOC与△
BOD全等吗?为什么?
O
A
B
C
D
两角和夹边对应相等
△
BOD
△
AOC
≌
\
(已知)
(中点的定义)
(对顶角相等)
解:在
中
(ASA)
变式:
如图,O是AB的中点,∠C=
∠D,
△AOC与△BOD全等吗?为什么?
O
A
B
C
D
两角和对边对应相等
BOD
AOC
D
≌
D
\
(已知)
(中点的定义)
(对顶角相等)
解:在
中
∠C=
∠D
(AAS)
针对练习:
1.如图∠B=∠DEF,
BC=EF,
求证:△ABC≌
△DEF
(1)若要以“SAS”为依据,还缺条件
;
(2)若要以“ASA”为依据,还缺条件
;
(3)若要以“SSS”
为依据,还缺条件
;
∠ACB=
∠DEF
AB=DE
AB=DE.AC=DF
(4)若要以“AAS”
为依据,还缺条件
;
∠A=
∠D
2.
已知,△ABC中,BE⊥
AD于E,CF⊥AD于点F,且BE=CF.那么BD与DC相等吗
全等三问:
①有什么条件;
②选择哪个判定;
③还缺什么条件。
3.
如图,AC、BD交于点O,AC=BD,AB=CD.
求证:
A
B
C
D
O
1
2
全等三问:
①有什么条件;
②选择哪个判定;
③还缺什么条件。
1.叙述“角边角”“ASA”.
2.叙述“角角边”“AAS”.
3.
全等证明的基本思路?
小结
12.2全等三角形的判定(三)
ASA
AAS
(2)
三条边
(1)
三个角
(3)
两边一角
(4)
两角一边
1、上一节课探究三角形全等条件时,两个三角形要全等至少要满足六个条件中的
时才成立,情况如下:
SSS
不能
?
SAS
三个
复习活动
A
B
C
A′
B′
C′
在图一中BC,B′C′
都是两个角的夹边。
观察:已知一个三角形的两角及一边,那么这两角及一边有几种可能的情况呢?
探索活动
观察:已知一个三角形的两角及一边,那么这两角及一边有几种可能的情况呢?
A
B
C
A′
B′
C′
在图中AB,A′
B′
不是两个角的夹边。
是其中一个角对边。
(1)如果已知两个三角形的两角及其夹边对应相等,那么这两个三角形全等吗?
A
B
C
A′
B′
C′
先任意画一个△ABC,再画一个△A′
B′
C′中使∠B=∠B′,BC=B′
C′,∠C
=∠C′(使两角及其夹边对应相等)再把画好的△A′B′C′减下来放在△ABC上,它们全等?。
画法:1、画B′
C′=BC;
2、在B′
C′
的同旁画∠DB′
C′=∠B
,
∠EC′B′
=∠C,
B′
D,C′
E交于点A′
。
B
A
C
B′
C′
A′
E
D
判定3:
两角和它们的夹边对应相等的两个三角形全等
(可以简写成“角边角”或“ASA”)。
∠A=∠A′
(已知
)
AB=A′
C(已知
)
∠B=∠C(已知
)
在△ABE和△A′
CD中
∴
△ABE≌△A′
CD(ASA)
A
S
A
用数学符号表示:
已知,在△ABE和△A′
CD中,AE=A′
D,∠A=∠A′
,∠B=∠C,求证△ABE≌△A′
CD
(2)两个角和其中一个角的对边对应相等的两个三角形全等吗?。
∠A=∠A′
(已知
)
∠B=∠C(已知
)
AE=A′
D(已知
)
在△ABE和△A′
CD中
∴
△ABE≌△A′
CD(AAS)
用数学符号表示:
判定4:两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)。
例1
已知:∠ABC=∠DCB,∠ACB=
∠DBC,
求证:
△
ABC
≌
△
DCB.
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
证明:
在ABC和△DCB中,
∴△ABC≌△DCB(ASA
).
B
C
A
D
巩固提升
例2.已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C。
求证:(1)AD=AE;
(2)BD=CE。
证明
:在△ADC和△AEB中
∠A=∠A(公共角)
AC=AB(已知)
∠C=∠B(已知)
∴△ACD≌△ABE(ASA)
∴AD=AE(全等三角形的对应边相等)
又∵AB=AC(已知)
∴BD=CE
小结:
到目前为止,我们一共探索出判定三角形全等的四种方法,它们分别是:
1、边边边
(SSS)
3、角边角
(ASA)
4、角角边
(AAS)
2、边角边
(SAS)
例3
如图,O是AB的中点,∠A=
∠B,
△
AOC与△
BOD全等吗?为什么?
O
A
B
C
D
两角和夹边对应相等
△
BOD
△
AOC
≌
\
(已知)
(中点的定义)
(对顶角相等)
解:在
中
(ASA)
变式:
如图,O是AB的中点,∠C=
∠D,
△AOC与△BOD全等吗?为什么?
O
A
B
C
D
两角和对边对应相等
BOD
AOC
D
≌
D
\
(已知)
(中点的定义)
(对顶角相等)
解:在
中
∠C=
∠D
(AAS)
针对练习:
1.如图∠B=∠DEF,
BC=EF,
求证:△ABC≌
△DEF
(1)若要以“SAS”为依据,还缺条件
;
(2)若要以“ASA”为依据,还缺条件
;
(3)若要以“SSS”
为依据,还缺条件
;
∠ACB=
∠DEF
AB=DE
AB=DE.AC=DF
(4)若要以“AAS”
为依据,还缺条件
;
∠A=
∠D
2.
已知,△ABC中,BE⊥
AD于E,CF⊥AD于点F,且BE=CF.那么BD与DC相等吗
全等三问:
①有什么条件;
②选择哪个判定;
③还缺什么条件。
3.
如图,AC、BD交于点O,AC=BD,AB=CD.
求证:
A
B
C
D
O
1
2
全等三问:
①有什么条件;
②选择哪个判定;
③还缺什么条件。
1.叙述“角边角”“ASA”.
2.叙述“角角边”“AAS”.
3.
全等证明的基本思路?
小结
