2021—2022学年人教版数学九年级上册23.1 图形的旋转 课件(21张ppt)
文档属性
| 名称 | 2021—2022学年人教版数学九年级上册23.1 图形的旋转 课件(21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
人教版初中数学九年级上学期23.1
图形的旋转(1)
1.
在生活实例中认识旋转,会举例,能类比平移的概念说出旋转的概念;
2.通过对图形旋转的观察、分析,能用语言叙述旋转的基本性质,并会用它解决相关问题;
3.在学习中感受“生活处处有数学”,在探索中学会合作与交流.
学习目标
A
B
C
A
●
A′
B′
C′
●
O
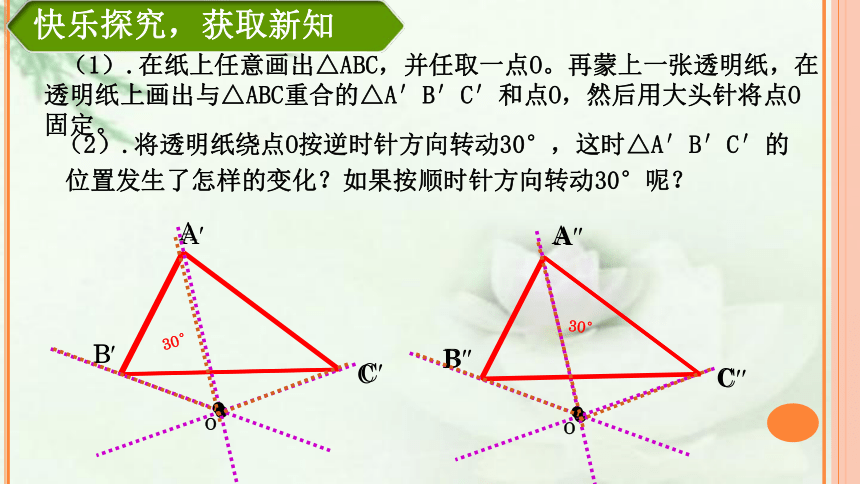
(2).将透明纸绕点O按逆时针方向转动30°,这时△A′B′C′的位置发生了怎样的变化?如果按顺时针方向转动30°呢?
30°
30°
A
●
A′′
B′′
C′′
●
O
A
B
C
(1).在纸上任意画出△ABC,并任取一点O。再蒙上一张透明纸,在透明纸上画出与△ABC重合的△A′B′C′和点O,然后用大头针将点O固定。
快乐探究,获取新知
1.什么是旋转
在平面内,将一个图形绕一个定点按某一个方向(逆时针方向或顺时针方向)转动一定的角度,图形的这种变化叫做旋转.
这个定点称为旋转中心,转动的角称为旋转角.
旋转前图形上的点与旋转后所到达的点叫做对应点
2.旋转的三要素:
旋转中心、旋转方向、旋转角.
形成概念
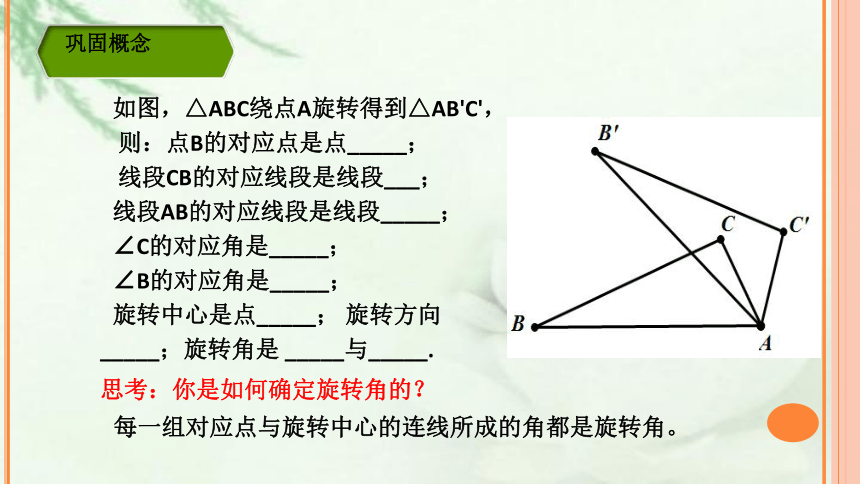
如图,△ABC绕点A旋转得到△AB'C',
则:点B的对应点是点_____;
线段CB的对应线段是线段___;
线段AB的对应线段是线段_____;
∠C的对应角是_____;
∠B的对应角是_____;
旋转中心是点_____;
旋转方向_____;旋转角是
_____与_____.
巩固概念
思考:你是如何确定旋转角的?
每一组对应点与旋转中心的连线所成的角都是旋转角。
A
B
C
A
●
A′
B′
C′
●
O
30°
30°
A
●
A′′
B′′
C′′
●
O
A
B
C
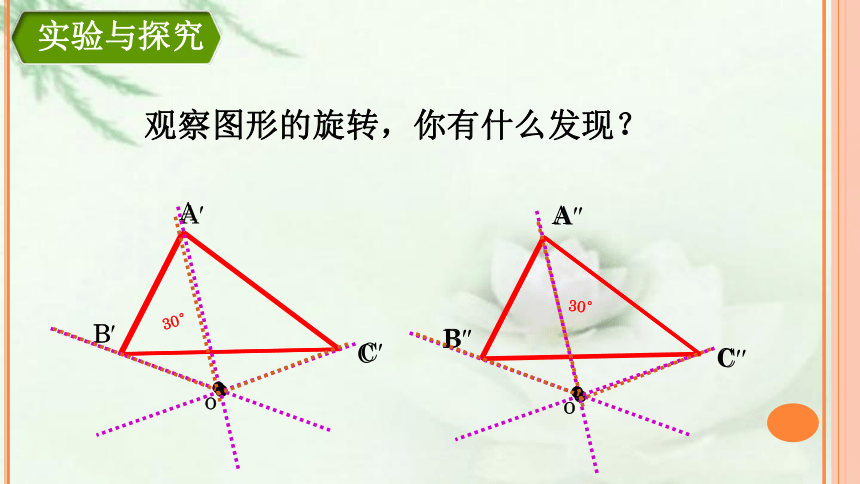
实验与探究
观察图形的旋转,你有什么发现?
1.对应点到旋转中心的距离相等;
2.两组对应点分别与旋转中心的
连线所成的角相等。
旋转的基本性质:
A'
O
A
45
0
点绕点转
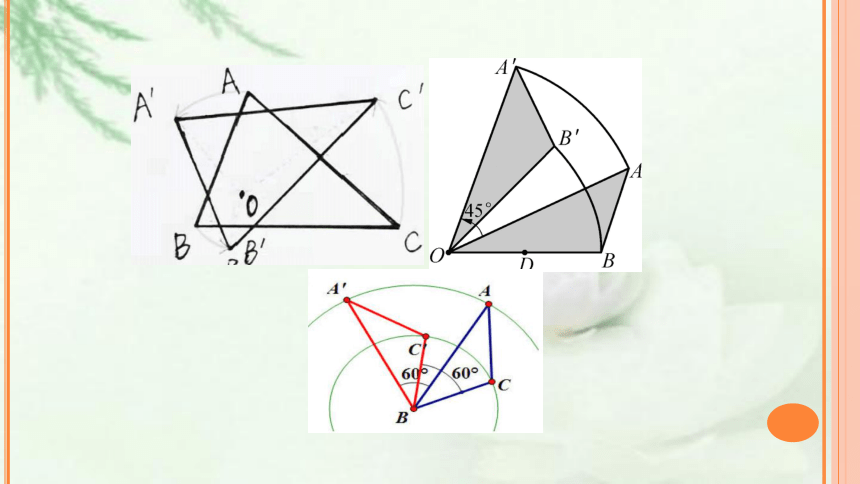
应用新知,体验成功
1、已知点A和点O,请画出点A绕点O按顺时针方向旋转45°后的图形.
动手画——点绕点转
A
O
所以,点A′就是所要求作的点。
A′
M
45°
步骤:一连线,二画角,三截取
所以,线段A′B′就是所要求作的线段。
A'
B'
B
A
D
C
2.已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形.
100°
100°
变式——线段旋转
O
①选择关键点;
②利用旋转的性质作已知图形点的对应点;
③连点成图。
变式——三角形旋转
已知△ABC和点O,请画出△ABC绕点O按顺时针旋转90°后的图形.
A
O
A′
B
B′
C
C′
所以,△A′B′C′就是所要求作的三角形。
╗
╗
╗
步骤:
思路:
关键:
反思:如何画图?
转
化
点旋转
形旋转
作已知图形点的对应点。
①选择关键点;②利用旋转的性质作已知图形点的对应点;③连点成图。
体会了...思想
学会了...知识
掌握了...方法
在...有待加强
教学目标
畅谈收获
1.下列现象中属于旋转的有(
)个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2
B.3
C.4
D.5
C
达标检测,当堂反馈
2.如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是__________,旋转角等于_________度,△ADP是___________三角形.
点A
60°
等边
3.四边形ABCD是正方形,△DAF逆时针旋转后与△DCE重合,那么
(1)旋转中心是哪一点?
(2)旋转角是几度?
(3)将△AFD绕A点顺时针旋转90度,旋转到△AHB,请判断△AHF形状.
H
D点
90
°
等腰直角三角形
你能用下面的图形结合我们今天所学的旋转知识设计一幅漂亮的图案吗?试一试!
动手做一做
学案页
练习1、2
作业
制作单位:曹县磐石街道办事处回民中学
录制时间:2021.5.24
人教版初中数学九年级上学期23.1
图形的旋转(1)
1.
在生活实例中认识旋转,会举例,能类比平移的概念说出旋转的概念;
2.通过对图形旋转的观察、分析,能用语言叙述旋转的基本性质,并会用它解决相关问题;
3.在学习中感受“生活处处有数学”,在探索中学会合作与交流.
学习目标
A
B
C
A
●
A′
B′
C′
●
O
(2).将透明纸绕点O按逆时针方向转动30°,这时△A′B′C′的位置发生了怎样的变化?如果按顺时针方向转动30°呢?
30°
30°
A
●
A′′
B′′
C′′
●
O
A
B
C
(1).在纸上任意画出△ABC,并任取一点O。再蒙上一张透明纸,在透明纸上画出与△ABC重合的△A′B′C′和点O,然后用大头针将点O固定。
快乐探究,获取新知
1.什么是旋转
在平面内,将一个图形绕一个定点按某一个方向(逆时针方向或顺时针方向)转动一定的角度,图形的这种变化叫做旋转.
这个定点称为旋转中心,转动的角称为旋转角.
旋转前图形上的点与旋转后所到达的点叫做对应点
2.旋转的三要素:
旋转中心、旋转方向、旋转角.
形成概念
如图,△ABC绕点A旋转得到△AB'C',
则:点B的对应点是点_____;
线段CB的对应线段是线段___;
线段AB的对应线段是线段_____;
∠C的对应角是_____;
∠B的对应角是_____;
旋转中心是点_____;
旋转方向_____;旋转角是
_____与_____.
巩固概念
思考:你是如何确定旋转角的?
每一组对应点与旋转中心的连线所成的角都是旋转角。
A
B
C
A
●
A′
B′
C′
●
O
30°
30°
A
●
A′′
B′′
C′′
●
O
A
B
C
实验与探究
观察图形的旋转,你有什么发现?
1.对应点到旋转中心的距离相等;
2.两组对应点分别与旋转中心的
连线所成的角相等。
旋转的基本性质:
A'
O
A
45
0
点绕点转
应用新知,体验成功
1、已知点A和点O,请画出点A绕点O按顺时针方向旋转45°后的图形.
动手画——点绕点转
A
O
所以,点A′就是所要求作的点。
A′
M
45°
步骤:一连线,二画角,三截取
所以,线段A′B′就是所要求作的线段。
A'
B'
B
A
D
C
2.已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形.
100°
100°
变式——线段旋转
O
①选择关键点;
②利用旋转的性质作已知图形点的对应点;
③连点成图。
变式——三角形旋转
已知△ABC和点O,请画出△ABC绕点O按顺时针旋转90°后的图形.
A
O
A′
B
B′
C
C′
所以,△A′B′C′就是所要求作的三角形。
╗
╗
╗
步骤:
思路:
关键:
反思:如何画图?
转
化
点旋转
形旋转
作已知图形点的对应点。
①选择关键点;②利用旋转的性质作已知图形点的对应点;③连点成图。
体会了...思想
学会了...知识
掌握了...方法
在...有待加强
教学目标
畅谈收获
1.下列现象中属于旋转的有(
)个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2
B.3
C.4
D.5
C
达标检测,当堂反馈
2.如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是__________,旋转角等于_________度,△ADP是___________三角形.
点A
60°
等边
3.四边形ABCD是正方形,△DAF逆时针旋转后与△DCE重合,那么
(1)旋转中心是哪一点?
(2)旋转角是几度?
(3)将△AFD绕A点顺时针旋转90度,旋转到△AHB,请判断△AHF形状.
H
D点
90
°
等腰直角三角形
你能用下面的图形结合我们今天所学的旋转知识设计一幅漂亮的图案吗?试一试!
动手做一做
学案页
练习1、2
作业
制作单位:曹县磐石街道办事处回民中学
录制时间:2021.5.24
同课章节目录
