2021-2022学年沪科版八年级数学上册_12.2.7 一次函数与一次方程、一次不等式 课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年沪科版八年级数学上册_12.2.7 一次函数与一次方程、一次不等式 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 516.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
数缺形时少直觉,形少数时难入微
华罗庚
一次函数与一次方程、一次不等式
12.2
一次函数(7)
1
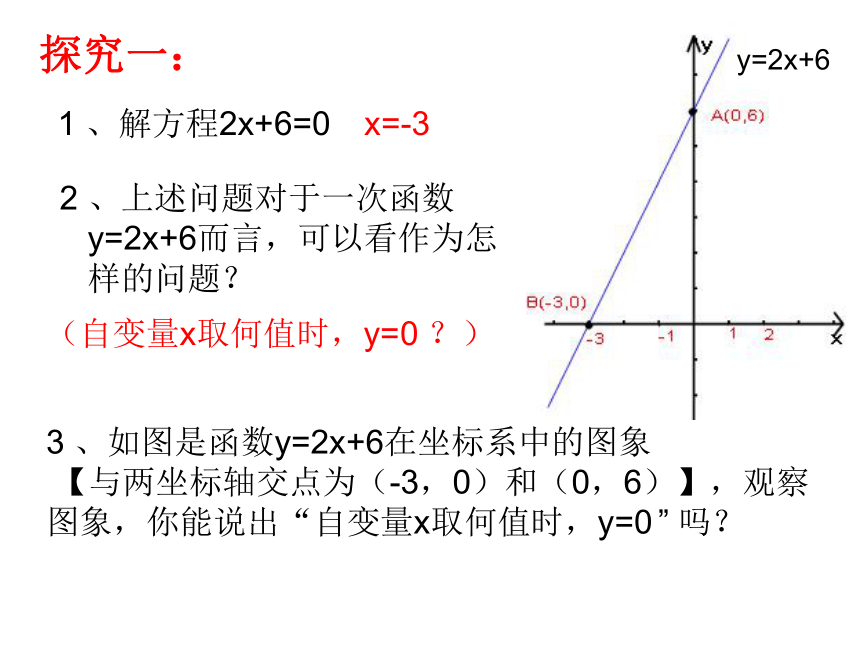
、解方程2x+6=0
y=2x+6
3
、如图是函数y=2x+6在坐标系中的图象
【与两坐标轴交点为(-3,0)和(0,6)】,观察图象,你能说出“自变量x取何值时,y=0
”
吗?
探究一:
x=-3
2
、上述问题对于一次函数
y=2x+6而言,可以看作为怎
样的问题?
(自变量x取何值时,y=0
?)
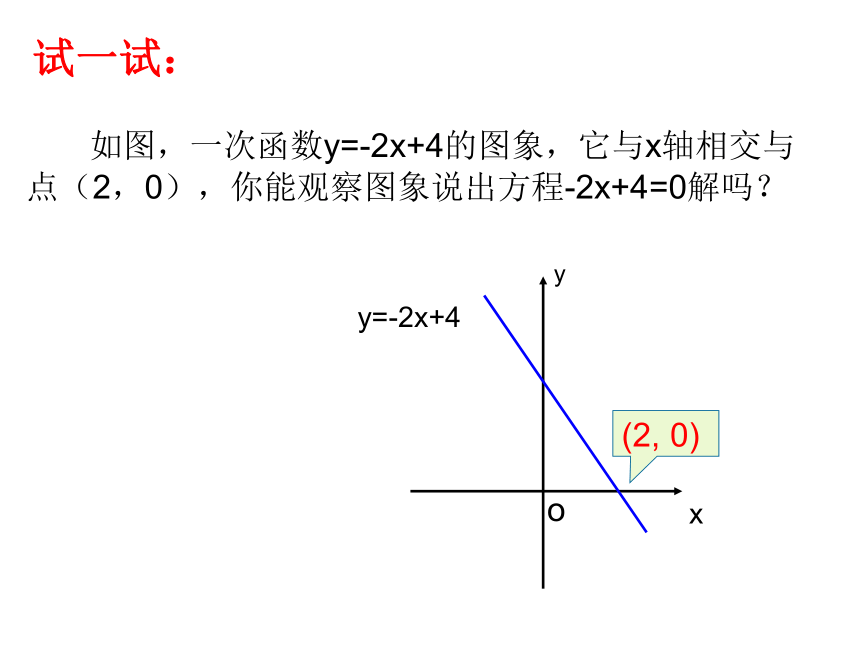
如图,一次函数y=-2x+4的图象,它与x轴相交与点(2,0),你能观察图象说出方程-2x+4=0解吗?
试一试:
y=-2x+4
x
y
(2,
0)
o
解一元一次方程kx+b=0(k≠0)
函数
y=kx+b中y=0时,求x的值
方程kx+b=0
解就是直线y=kx+b与x轴交点横坐标
(可看作为)
(从图象上看)
归纳:
议一议:
你能归纳从“求一元一次方程kx+b=0的解”到“观察函数y=kx+b图象,得到解”的过程吗?(分组讨论)
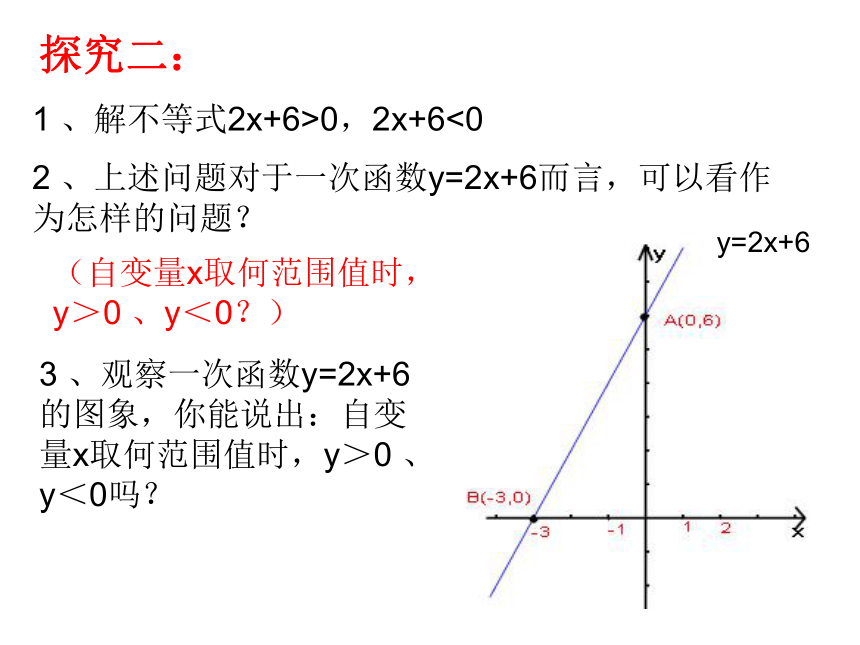
1
、解不等式2x+6>0,2x+6<0
2
、上述问题对于一次函数y=2x+6而言,可以看作为怎样的问题?
探究二:
3
、观察一次函数y=2x+6
的图象,你能说出:自变
量x取何范围值时,y>0
、
y<0吗?
y=2x+6
(自变量x取何范围值时,
y>0
、y<0?)
y=2x+6
y>0
x>-3
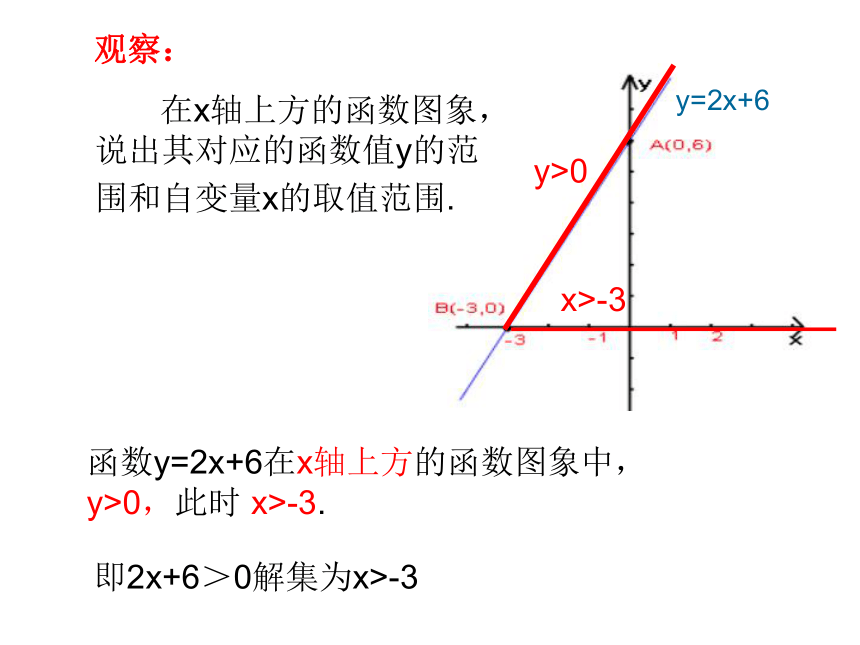
在x轴上方的函数图象,
说出其对应的函数值y的范
函数y=2x+6在x轴上方的函数图象中,
y>0,此时
x>-3.
围和自变量x的取值范围.
即2x+6>0解集为x>-3
观察:
X<-3
y=2x+6
观察:
y<0
x<-3
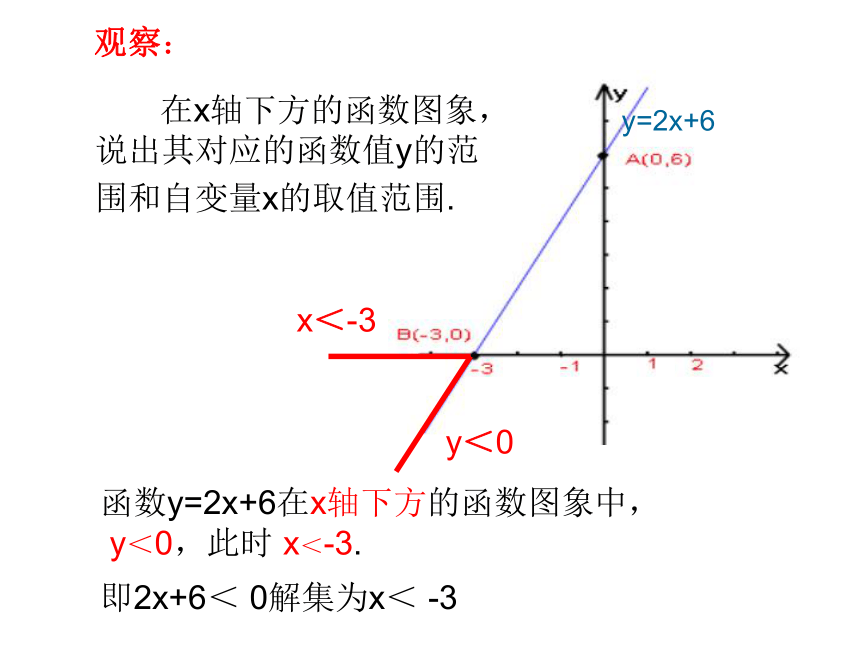
函数y=2x+6在x轴下方的函数图象中,
y<0,此时
x<-3.
在x轴下方的函数图象,
说出其对应的函数值y的范
围和自变量x的取值范围.
即2x+6<
0解集为x<
-3
求一元一次不等式kx+b>0
(或kx+b<0)的解集
kx+b>0
(或kx+b<0)的解集是直线y=kx+b位于x轴上方(或下方)部分对应x的取值范围.
(可看作为)
(从图象上看)
归纳:
函数
y=kx+b中y>0(或y<0)时,求x的取值范围
议一议:
你能归纳从“求一次不等式kx+b>0
(或kx+b<0)的解集”到“观察函数y=kx+b图象,得到解集”
过程吗?(分组讨论)
·
·
4
例题:画出函数y=-3x+6的图象,观察图象:
(1)求方程-3x+6=0的解;
(2)求不等式-3x+6>0
和-3x+6<0的解集。
解:可求图象与x轴,y轴的交点为(2,0)和(0,6),描点并
连线画出函数图象。
x
y
-6
-4
-2
-2
-4
0
2
6
2
4
6
(1)方程-3x+6=0的
解是x=2.
(2)不等式-3x+6>0
解集是x<2;
不等式-3x+6<0
解集是x>2。
观察图象可知:
想一想1、点(1,3)在函数y=-3x+6的图象上吗?
2、观察图象,说出方程-3x+6=3的解;
-4
x
y
-6
-4
-2
-2
0
2
4
6
2
4
6
y=-3x+6
x<1
x>1
X=1
·(1,3)
3、求不等式-3x+6>3和-3x+6<3的解集。
1、
已知关于x的方程mx+n=0的解是
x=-2,则直线y=mx+n与x轴的交
点坐标是______.
(-2,0)
练一练:
2、由图可知不等式-x+b≤0的解集是
______。
x
y
y=-x+b
(
3,
0
)
x≥3
·(3,4)
x
y
-3
-2
-1
-1
-2
0
1
2
3
1
2
3
4
5
4
5
y
1=kx+b
3
、如图,是一次函数y
=kx+b的
图象,图象与两坐标轴交点
分别为(1,0),(0,-2)
。另外点(3,4)也在图象上
,观察图象回答下列问题:
(1)x____时,
y
=0
x____时,
y
>0
x____时,
y
<0
(2)x
<0
时,
y
____
x
>3时
,
y
____
=1
>1
<
1
<
-2
>4
·(3,4)
x
y
-3
-2
-1
-1
-2
0
1
2
3
1
2
3
4
5
4
5
y
1=kx+b
y2=mx+n
3
、如图,是一次函数y
=kx+b的
图象,图象与两坐标轴交点
分别为(1,0),(0,-2)
。另外点(3,4)也在图象上
,观察图象回答下列问题:
(1)x____时,
y
=0
x____时,
y
>0
x____时,
y
<0
(2)x
<0
时,
y
____
x
>3时
,
y
____
(3)【课后思考】直线y2=mx+n图象如图示,经过点
(3,4),x为何范围内值是,
y1
=y2
,
y1
>
y2,
y1
<
y2?
=1
>1
<
1
<
-2
>4
课堂总结:
1、把你的收获请与同学分享
(知识,方法或
经验和感悟)
2、把你的疑惑告诉老师
作业布置:
1、(必做题)习题12.2
第17,18,19题
2、(选做题)通过本节课的学习,你对“一次函数与一次方程、一次不等式”的联系有了一定的认识,请写一篇600字左右的数学小论文,谈谈你的认识或理解。
数缺形时少直觉,形少数时难入微
华罗庚
一次函数与一次方程、一次不等式
12.2
一次函数(7)
1
、解方程2x+6=0
y=2x+6
3
、如图是函数y=2x+6在坐标系中的图象
【与两坐标轴交点为(-3,0)和(0,6)】,观察图象,你能说出“自变量x取何值时,y=0
”
吗?
探究一:
x=-3
2
、上述问题对于一次函数
y=2x+6而言,可以看作为怎
样的问题?
(自变量x取何值时,y=0
?)
如图,一次函数y=-2x+4的图象,它与x轴相交与点(2,0),你能观察图象说出方程-2x+4=0解吗?
试一试:
y=-2x+4
x
y
(2,
0)
o
解一元一次方程kx+b=0(k≠0)
函数
y=kx+b中y=0时,求x的值
方程kx+b=0
解就是直线y=kx+b与x轴交点横坐标
(可看作为)
(从图象上看)
归纳:
议一议:
你能归纳从“求一元一次方程kx+b=0的解”到“观察函数y=kx+b图象,得到解”的过程吗?(分组讨论)
1
、解不等式2x+6>0,2x+6<0
2
、上述问题对于一次函数y=2x+6而言,可以看作为怎样的问题?
探究二:
3
、观察一次函数y=2x+6
的图象,你能说出:自变
量x取何范围值时,y>0
、
y<0吗?
y=2x+6
(自变量x取何范围值时,
y>0
、y<0?)
y=2x+6
y>0
x>-3
在x轴上方的函数图象,
说出其对应的函数值y的范
函数y=2x+6在x轴上方的函数图象中,
y>0,此时
x>-3.
围和自变量x的取值范围.
即2x+6>0解集为x>-3
观察:
X<-3
y=2x+6
观察:
y<0
x<-3
函数y=2x+6在x轴下方的函数图象中,
y<0,此时
x<-3.
在x轴下方的函数图象,
说出其对应的函数值y的范
围和自变量x的取值范围.
即2x+6<
0解集为x<
-3
求一元一次不等式kx+b>0
(或kx+b<0)的解集
kx+b>0
(或kx+b<0)的解集是直线y=kx+b位于x轴上方(或下方)部分对应x的取值范围.
(可看作为)
(从图象上看)
归纳:
函数
y=kx+b中y>0(或y<0)时,求x的取值范围
议一议:
你能归纳从“求一次不等式kx+b>0
(或kx+b<0)的解集”到“观察函数y=kx+b图象,得到解集”
过程吗?(分组讨论)
·
·
4
例题:画出函数y=-3x+6的图象,观察图象:
(1)求方程-3x+6=0的解;
(2)求不等式-3x+6>0
和-3x+6<0的解集。
解:可求图象与x轴,y轴的交点为(2,0)和(0,6),描点并
连线画出函数图象。
x
y
-6
-4
-2
-2
-4
0
2
6
2
4
6
(1)方程-3x+6=0的
解是x=2.
(2)不等式-3x+6>0
解集是x<2;
不等式-3x+6<0
解集是x>2。
观察图象可知:
想一想1、点(1,3)在函数y=-3x+6的图象上吗?
2、观察图象,说出方程-3x+6=3的解;
-4
x
y
-6
-4
-2
-2
0
2
4
6
2
4
6
y=-3x+6
x<1
x>1
X=1
·(1,3)
3、求不等式-3x+6>3和-3x+6<3的解集。
1、
已知关于x的方程mx+n=0的解是
x=-2,则直线y=mx+n与x轴的交
点坐标是______.
(-2,0)
练一练:
2、由图可知不等式-x+b≤0的解集是
______。
x
y
y=-x+b
(
3,
0
)
x≥3
·(3,4)
x
y
-3
-2
-1
-1
-2
0
1
2
3
1
2
3
4
5
4
5
y
1=kx+b
3
、如图,是一次函数y
=kx+b的
图象,图象与两坐标轴交点
分别为(1,0),(0,-2)
。另外点(3,4)也在图象上
,观察图象回答下列问题:
(1)x____时,
y
=0
x____时,
y
>0
x____时,
y
<0
(2)x
<0
时,
y
____
x
>3时
,
y
____
=1
>1
<
1
<
-2
>4
·(3,4)
x
y
-3
-2
-1
-1
-2
0
1
2
3
1
2
3
4
5
4
5
y
1=kx+b
y2=mx+n
3
、如图,是一次函数y
=kx+b的
图象,图象与两坐标轴交点
分别为(1,0),(0,-2)
。另外点(3,4)也在图象上
,观察图象回答下列问题:
(1)x____时,
y
=0
x____时,
y
>0
x____时,
y
<0
(2)x
<0
时,
y
____
x
>3时
,
y
____
(3)【课后思考】直线y2=mx+n图象如图示,经过点
(3,4),x为何范围内值是,
y1
=y2
,
y1
>
y2,
y1
<
y2?
=1
>1
<
1
<
-2
>4
课堂总结:
1、把你的收获请与同学分享
(知识,方法或
经验和感悟)
2、把你的疑惑告诉老师
作业布置:
1、(必做题)习题12.2
第17,18,19题
2、(选做题)通过本节课的学习,你对“一次函数与一次方程、一次不等式”的联系有了一定的认识,请写一篇600字左右的数学小论文,谈谈你的认识或理解。
