2021-2022学年苏科新版九年级上册数学《第4章 等可能条件下的概率》单元测试卷(word版、含解析)
文档属性
| 名称 | 2021-2022学年苏科新版九年级上册数学《第4章 等可能条件下的概率》单元测试卷(word版、含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 285.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览



文档简介
2021-2022学年苏科新版九年级上册数学《第4章
等可能条件下的概率》单元测试卷
一.选择题
1.从一副普通的54张的扑克牌中随意抽出一张,有4个事件:①抽到大王;②抽到小王;③抽到2;④抽到梅花.则这4个事件发生的可能性最大的是( )
A.①
B.②
C.③
D.④
2.一个袋子中有15个红球,5个白球,每个球除颜色外都相同,任意摸出一个球,摸到( )的可能性较大.
A.红球
B.蓝球
C.白球
D.都一样
3.一只不透明的袋子中装有3个白球,4个黄球,6个红球,每个球除颜色外都相同,从袋子中随机摸出一个球,下列说法正确的是( )
A.摸到红球的可能性最大
B.摸到黄球的可能性最大
C.摸到白球的可能性最大
D.摸到三种颜色的球的可能性一样大
4.小张抛一枚质地均匀的硬币,出现正面朝上的可能性是( )
A.25%
B.50%
C.75%
D.85%
5.从标有1,2,3…,20的20张卡片中任意抽取一张,可能性最大的是( )
A.卡片上的数字是4的倍数
B.卡片上的数字是2的倍数
C.卡片上的数字是5的倍数
D.卡片上的数字是3的倍数
6.如图是一个可以自由转动的转盘,转盘分成黑、白两种颜色指针的位置固定,转动的转盘停止后,指针恰好指向白色扇形的穊率为(指针指向OA时,当作指向黑色扇形;指针指OB时,当作指向白色扇形),则黑色扇形的圆心角∠AOB=( )
A.40°
B.45°
C.50°
D.60°
7.小明已有两根长度分别是3cm和6cm的细竹签,盒子里面有四根长度分别是3cm,4cm,7cm,8cm的细竹签,小明随意从盒子里面抽取一个细竹签,恰能与已有两根细竹签首尾顺次连接成三角形的概率是( )
A.
B.
C.
D.1
8.如图,在△ABC中,D是线段AB上的点,且AD:DB=1:2,F是线段BC上的点,DE∥BC,FE∥BA,小亮同学随机在△ABC内部区域投针,则针扎到△DEF(阴影)区域内的概率是( )
A.
B.
C.
D.
9.某十字路口的交通信号灯,红灯亮50秒,绿灯亮40秒,黄灯亮10秒.当你抬头看信号灯时,是红灯的概率为( )
A.
B.
C.
D.
10.不透明袋子中有除颜色外完全相同的4个黑球和2个白球,从袋子中随机摸出3个球,则概率最大的是( )
A.3个都是黑球
B.2个黑球1个白球
C.2个白球1个黑球
D.至少有1个黑球
二.填空题
11.从一副扑克牌中任意抽取一张.
(1)这张牌是“A”;
(2)这张牌是“红心”;
(3)这张牌是“大王”;
(4)这张牌是“红色的”.
将这些事件的序号按发生的可能性从小到达顺序排列是
.
12.一个箱子装有除颜色外都相同的2个白球,2个黄球,1个红球.现添加上述同种型号的1个球,使得从中随机抽取1个球,白颜色的球被抽到的可能性是,那么添加的球是
.
13.从一副扑克牌中任意抽取1张.
①这张牌是“A”;
②这张牌是“红桃”;
③这张牌是“大王”;
④这张牌是“红色的”.
将这些事件按发生的可能性从小到大顺序排列
.(填序号,用“<”连接)
14.一个小球在如图所示的地面上自由滚动,并随机地停留在某块方砖上,则小球停留在黑色区域的概率是
.
15.在一所有1500名学生的中学里,调查人员随机调查了50名学生,其中有40人每天都喝牛奶,那么在这所学校里,随便询问1人,每天都喝牛奶的概率是
.
16.小明与小颖用一副去掉大王和小王的扑克牌做摸牌游戏:小明从中任意摸一张牌(不放回),小颖从剩余的牌中任意摸一张,谁摸到的牌面大,谁就获胜(规定牌面从小到大的顺序为2,3,4,5,6,7,8,9,10,J,Q,K,A),然后两人把摸到的牌都放回,重新开始游戏,若小明已经摸到的牌面为4,然后小颖摸牌,那么小明获胜的概率是
.
17.欧阳修在《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”.如图所示,可见卖油翁的技艺之高超,若铜钱直径为4cm,中间有边长为1cm的正方形小孔,随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入口中的概率是
.
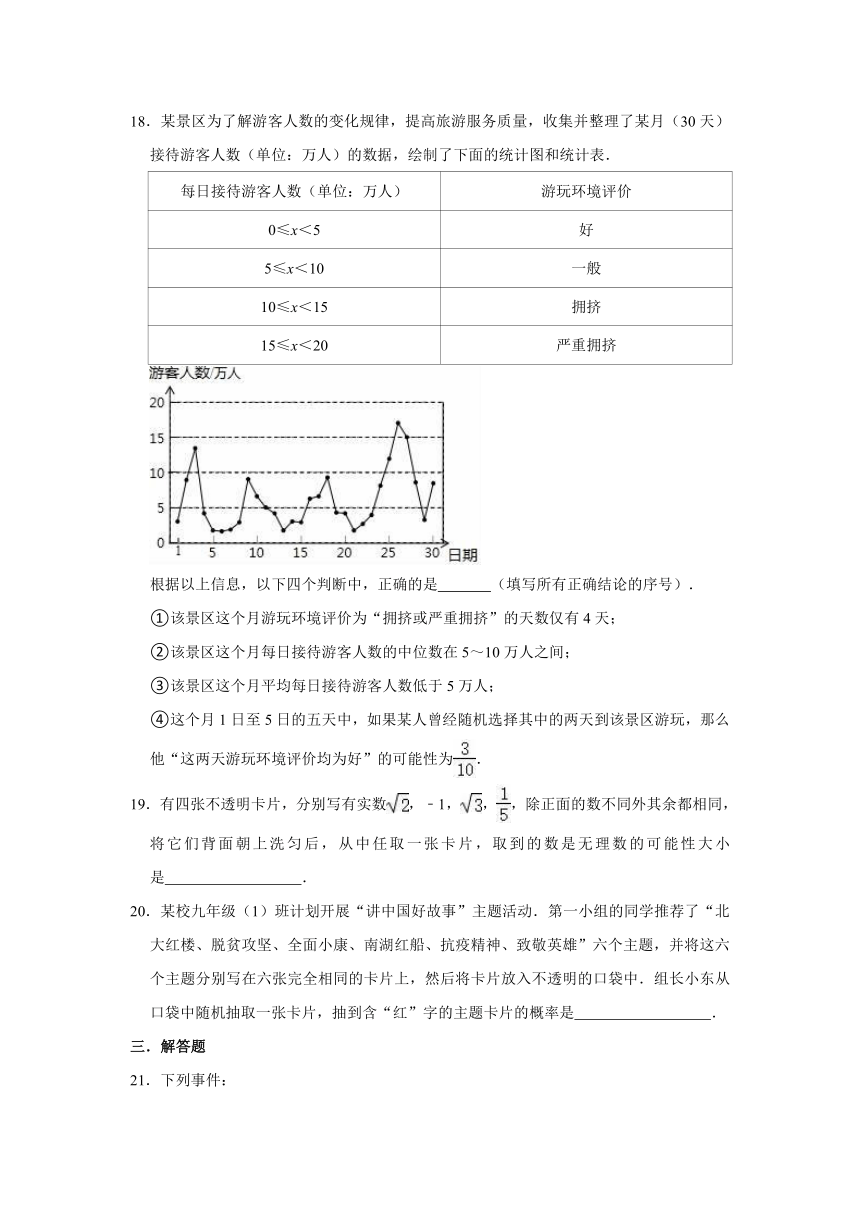
18.某景区为了解游客人数的变化规律,提高旅游服务质量,收集并整理了某月(30天)接待游客人数(单位:万人)的数据,绘制了下面的统计图和统计表.
每日接待游客人数(单位:万人)
游玩环境评价
0≤x<5
好
5≤x<10
一般
10≤x<15
拥挤
15≤x<20
严重拥挤
根据以上信息,以下四个判断中,正确的是
(填写所有正确结论的序号).
①该景区这个月游玩环境评价为“拥挤或严重拥挤”的天数仅有4天;
②该景区这个月每日接待游客人数的中位数在5~10万人之间;
③该景区这个月平均每日接待游客人数低于5万人;
④这个月1日至5日的五天中,如果某人曾经随机选择其中的两天到该景区游玩,那么他“这两天游玩环境评价均为好”的可能性为.
19.有四张不透明卡片,分别写有实数,﹣1,,,除正面的数不同外其余都相同,将它们背面朝上洗匀后,从中任取一张卡片,取到的数是无理数的可能性大小是
.
20.某校九年级(1)班计划开展“讲中国好故事”主题活动.第一小组的同学推荐了“北大红楼、脱贫攻坚、全面小康、南湖红船、抗疫精神、致敬英雄”六个主题,并将这六个主题分别写在六张完全相同的卡片上,然后将卡片放入不透明的口袋中.组长小东从口袋中随机抽取一张卡片,抽到含“红”字的主题卡片的概率是
.
三.解答题
21.下列事件:
(1)从装有1个红球和2个黄球的袋子中摸出的1个球是白球;
(2)随意调查1位青年,他接受过九年制义务教育;
(3)花2元买一张体育彩票,喜中500万大奖;
(4)抛掷1个小石块,石块会下落.
估计这些事件的可能性大小,在相应位置填上序号.
一定会发生的事件:
;
发生的可能性非常大的事件:
;
发生的可能性非常小的事件:
;
不可能发生的事件:
.
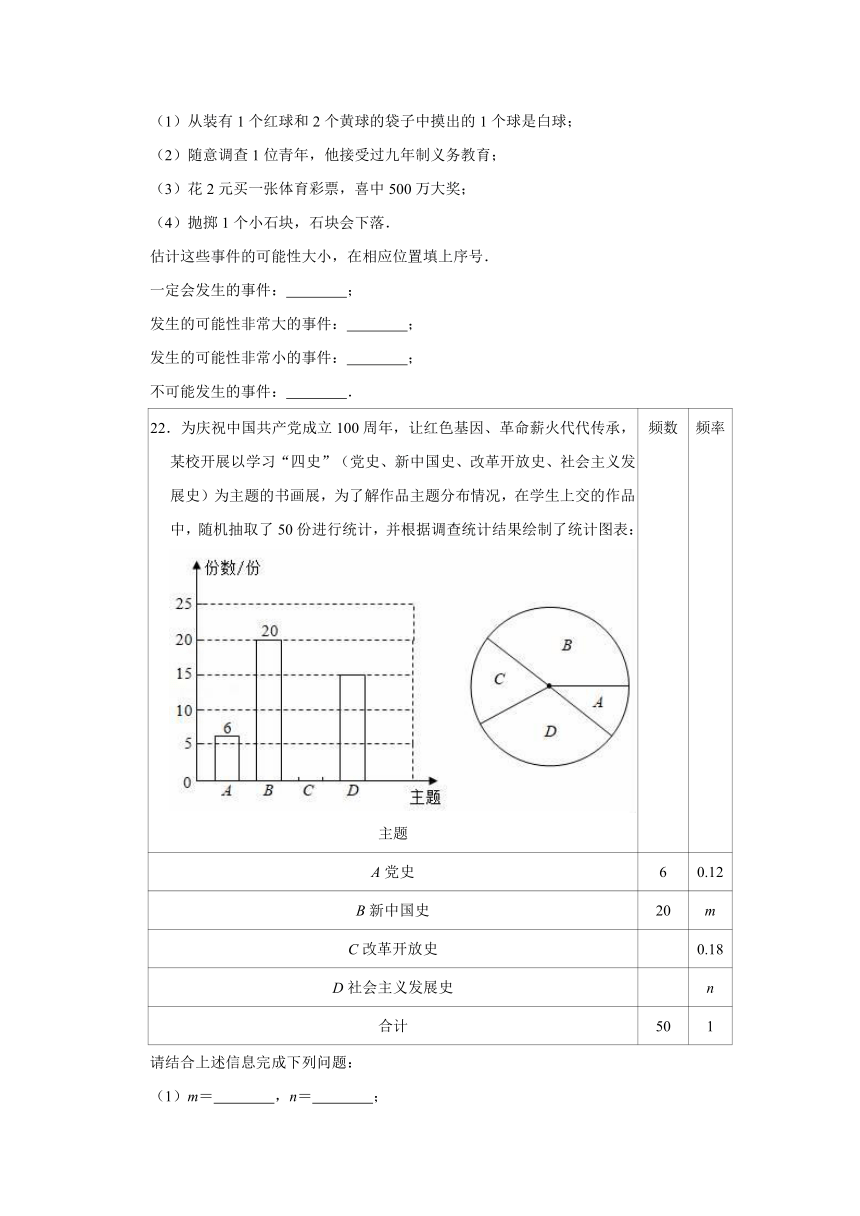
22.为庆祝中国共产党成立100周年,让红色基因、革命薪火代代传承,某校开展以学习“四史”(党史、新中国史、改革开放史、社会主义发展史)为主题的书画展,为了解作品主题分布情况,在学生上交的作品中,随机抽取了50份进行统计,并根据调查统计结果绘制了统计图表:主题
频数
频率
A党史
6
0.12
B新中国史
20
m
C改革开放史
0.18
D社会主义发展史
n
合计
50
1
请结合上述信息完成下列问题:
(1)m=
,n=
;
(2)请补全条形统计图;
(3)在扇形统计图中,“新中国史”主题作品份数对应的圆心角是
度;
(4)若该校同时开设两门课程,则开设课程B、C的概率为
.
23.如图是一个转盘.转盘分成8个相同的图形,颜色分为红、绿、黄三种.指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个图形的交线时,当作指向右边的图形).求下列事件的概率:
(1)指针指向红色;
(2)指针指向黄色或绿色.
24.“扫雷”是一个有趣的游戏,如图是此游戏的一部分:
图中数字2表示以该数字为中心的8个方格中有2个地雷,小旗表示该方格已被探明有地雷,现在还剩下A,B,C三个方格未被探明,其它地方为安全区(包括有数字的方格).试问:
(1)现在还剩下几个地雷?
(2)A,B,C三个方格中有地雷的概率分别是多少?
25.有两个盒子,分别装有若干个除颜色外都相同的球,第一个盒子装有4个红球和6个白球,第二个盒子装有6个红球和6个白球.分别从这两个盒子中各摸出1个球,请你通过计算来判断从哪一个盒子中摸出白球的可能性大.
26.一只不透明的袋子中装有1个白球、2个黄球和3个红球,每个球除颜色外都相同,将球摇匀,从中任意摸出一个球:
(1)该球是白球;
(2)该球是黄球;
(3)该球是红球.
估计上述事件发生的可能性的大小,将这些事件的序号按发生的可能性从小到大的顺序排列.
参考答案与试题解析
一.选择题
1.解:一副普通的54张的扑克牌中,①大王有一张;②小王有一张;③2有4张;④梅花有13张;
∵13>4>1,
∴这4个事件发生的可能性最大的是④.
故选:D.
2.解:根据题意可知:摸到红色球的可能性为=,
摸到白色球的可能性为=,
故摸到红色球的可能性大.
故选:A.
3.解:摸到白球的可能性为,摸到黄球的可能性为,摸到红球的可能性为,
所以摸到红球的可能性最大,
故选:A.
4.解:抛一枚质地均匀的硬币,有正面朝上、反面朝上两种结果,故正面朝上的概率=.
故选:B.
5.解:A、卡片上的数字是4的倍数的有4×1,4×2,4×3,4×4,4×5,共5张;
B、卡片上的数字是2的倍数2×1,2×2,2×3,2×4,2×5,2×6,2×7,2×8,2×9,2×10,共10张;
C、卡片上的数字是5的倍数5×1,5×2,5×3,5×4,共4张;
D、卡片上的数字是3的倍数3×1,3×2,3×3,3×4,3×5,3×6,共6张.
故选:B.
6.解:∵指针恰好指向白色扇形的穊率为,
∴黑、白两种颜色的扇形的面积比为1:7,
∴∠AOB=×360°=45°,
故选:B.
7.解:设第3根竹签长为xcm,
∵已有两根长度分别是3cm和6cm的细竹签,
∴第三根可以构成三角形的范围是:3<x<9,
其中4cm,7cm,8cm符合题意,
则小明从盒子里随意抽取一根细竹签,恰能与已有的两根细竹签首尾顺次联结组成三角形的概率是:.
故选:C.
8.解:∵AD:DB=1:2,DE∥BC,
∴AE:EC=1:2,
∵FE∥BA,
∴CF:BF=2:1,
∴△BDF的面积=××△ABC的面积=×△ABC的面积,
△ADE的面积=××△ABC的面积=×△ABC的面积,
△BDF的面积=××△ABC的面积=×△ABC的面积,
∴△DEF(阴影)区域内的面积=×△ABC的面积,
∴针扎到△DEF(阴影)区域内的概率是÷1=.
故选:B.
9.解:∵某十字路口的交通信号灯,红灯亮50秒,绿灯亮40秒,黄灯亮10秒,
∴当你抬头看信号灯时,是红灯的概率为:=
故选:A.
10.解:A、袋子中装有4个黑球和2个白球,摸出的三个球中可能为两个白球一个黑球,
∴3个都是黑球的概率小于1;
B、袋子中有4个黑球,有可能摸到的全部是黑球,B有可能不发生,
∴2个黑球1个白球的概率小于1;
C、袋子中有4个黑球,有可能摸到的全部是黑球,C有可能不发生,
∴2个白球1个黑球的概率小于1;
D、白球只有两个,如果摸到三个球不可能都是白梂,因此至少有一个是黑球,
∴至少有1个黑球的概率为1,
故选:D.
二.填空题
11.解:从一副扑克牌中任意抽取一张,
(1)这张牌是“A”的概率为=;
(2)这张牌是“红心”的概率为;
(3)这张牌是“大王”的概率为;
(4)这张牌是“红色的”的概率为=,
∴(3)<(1)<(2)<(4),
故答案为:(3)<(1)<(2)<(4).
12.解:∵2÷(2+2+1)=,
∴原来白颜色的球被抽到的可能性是;
∵>,
∴添加的球是红球或黄球.
故答案为:红球或黄球.
13.解:一副扑克牌中含“A”4张,“红桃”13张,“大王”1张,“红色的”26张,
∵1<4<13<26,
∴将这些事件按发生的可能性从小到大顺序排列:③①②④.
故答案为:③①②④.
14.解:由图可知:黑色区域在整个地面中所占的比值=,
∴小球最终停留在黑色区域的概率=,
故答案为:.
15.解:在这所学校里,随便询问1人,每天都喝牛奶的概率是=,
故答案为:.
16.解:由题意知,去掉大王、小王的扑克牌共有52张,其中比4小的牌有2,3,
∴小明获胜的概率是=,
故答案为:.
17.解:∵直径为4cm的铜钱的面积=π×22=4π,边长为1cm的正方形小孔的面积=1×1=1,
∴随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入口中的概率=;
故答案为:.
18.解:①根据题意每日接待游客人数10≤x<15为拥挤,15≤x<20为严重拥挤,
由统计图可知,游玩环境评价为“拥挤或严重拥挤”,1日至5日有1天,25日﹣30日有3天,共4天,故①正确;
②本题中位数是指将30天的游客人数从小到大排列,第15与第16位的和除以2,
根据统计图可知0≤x<5的有16天,从而中位数位于0≤x<5范围内,故②错误;
③从统计图可以看出,接近10的有6天,大于10而小于15的有2天,15以上的有2天,
10上下的估算为10,则(10×8+15×2﹣5×10)÷16=3.25,
可以考虑为给每个0至5的补上3.25,则大部分大于5,而0至5范围内有6天接近5,故平均数一定大于5,故③错误;
④由题意可知“这两天游玩环境评价均为好”的可能性为:×=,故④正确.
故答案为:①④.
19.解:∵实数,﹣1,,中,,是无限不循环小数,
∴无理数有2个,
∴取到的数是无理数的可能性大小是:
2÷4=.
故答案为:.
20.解:含“红”字的主题卡片有“北大红楼”和“南湖红船”共2张,
所以抽到含“红”字的主题卡片的概率是.
故答案为:.
三.解答题
21.解:(1)从装有1个红球和2个黄球的袋子中摸出的1个球是白球的概率是0,不可能发生;
(2)随意调查1位青年,他接受过九年制义务教育概率较大,发生的可能性较大;
(3)花2元买一张体育彩票,喜中500万大奖,概率较小,发生的可能性较小;
(4)抛掷1个小石块,石块会下落,概率为1,一定会发生.
故答案为:(4);(2);(3);(1).
22.解:(1)由统计图表可知:
m==0.4,
∴n=1﹣0.12﹣0.18﹣0.4=0.3,
故m=0.4,n=0.3;
(2)结果如下:
(3)∵新中国史的频率为0.4,
∴360°×0.4=144°,
∴“新中国史”主题作品份数对应的圆心角是144°;
(4)列表如下:
∴一共有12种情况,开设课程B,C的有2种情况,
∴开设课程B、C的概率为:P=.
23.解:按颜色把8个扇形分为红1、红2、绿1、绿2、绿3、黄1、黄2、黄3,所有可能结果的总数为8,
(1)指针指向红色的结果有2个,
∴P(指针指向红色)=;
(2)指针指向黄色或绿色的结果有3+3=6个,
∴P(指针指向黄色或绿色)==.
24.解:(1)∵于B、C下面标2,说明它们为中心的8个方格中有2个地雷,而C的右边已经有一个,
∴A就是一个地雷,还有一个可能在B、C的位置,
∴现在还剩下2个地雷;
(2)根据(1)得
P(A有地雷)=1,
P(B有地雷)=,
P(C有地雷)=.
25.解:P(从第一个盒子中摸出一个白球)=,
P(从第二个盒子中摸出一个白球)=,
∵,
∴第一个盒子中摸到白球的可能性大.
26.解:∵不透明的袋子中装有1个白球、2个黄球和3个红球,
∴摸到白球的概率为,
摸到黄球的概率为=,
摸到红球的概率为=,
∵,
∴(1)<(2)<(3).
等可能条件下的概率》单元测试卷
一.选择题
1.从一副普通的54张的扑克牌中随意抽出一张,有4个事件:①抽到大王;②抽到小王;③抽到2;④抽到梅花.则这4个事件发生的可能性最大的是( )
A.①
B.②
C.③
D.④
2.一个袋子中有15个红球,5个白球,每个球除颜色外都相同,任意摸出一个球,摸到( )的可能性较大.
A.红球
B.蓝球
C.白球
D.都一样
3.一只不透明的袋子中装有3个白球,4个黄球,6个红球,每个球除颜色外都相同,从袋子中随机摸出一个球,下列说法正确的是( )
A.摸到红球的可能性最大
B.摸到黄球的可能性最大
C.摸到白球的可能性最大
D.摸到三种颜色的球的可能性一样大
4.小张抛一枚质地均匀的硬币,出现正面朝上的可能性是( )
A.25%
B.50%
C.75%
D.85%
5.从标有1,2,3…,20的20张卡片中任意抽取一张,可能性最大的是( )
A.卡片上的数字是4的倍数
B.卡片上的数字是2的倍数
C.卡片上的数字是5的倍数
D.卡片上的数字是3的倍数
6.如图是一个可以自由转动的转盘,转盘分成黑、白两种颜色指针的位置固定,转动的转盘停止后,指针恰好指向白色扇形的穊率为(指针指向OA时,当作指向黑色扇形;指针指OB时,当作指向白色扇形),则黑色扇形的圆心角∠AOB=( )
A.40°
B.45°
C.50°
D.60°
7.小明已有两根长度分别是3cm和6cm的细竹签,盒子里面有四根长度分别是3cm,4cm,7cm,8cm的细竹签,小明随意从盒子里面抽取一个细竹签,恰能与已有两根细竹签首尾顺次连接成三角形的概率是( )
A.
B.
C.
D.1
8.如图,在△ABC中,D是线段AB上的点,且AD:DB=1:2,F是线段BC上的点,DE∥BC,FE∥BA,小亮同学随机在△ABC内部区域投针,则针扎到△DEF(阴影)区域内的概率是( )
A.
B.
C.
D.
9.某十字路口的交通信号灯,红灯亮50秒,绿灯亮40秒,黄灯亮10秒.当你抬头看信号灯时,是红灯的概率为( )
A.
B.
C.
D.
10.不透明袋子中有除颜色外完全相同的4个黑球和2个白球,从袋子中随机摸出3个球,则概率最大的是( )
A.3个都是黑球
B.2个黑球1个白球
C.2个白球1个黑球
D.至少有1个黑球
二.填空题
11.从一副扑克牌中任意抽取一张.
(1)这张牌是“A”;
(2)这张牌是“红心”;
(3)这张牌是“大王”;
(4)这张牌是“红色的”.
将这些事件的序号按发生的可能性从小到达顺序排列是
.
12.一个箱子装有除颜色外都相同的2个白球,2个黄球,1个红球.现添加上述同种型号的1个球,使得从中随机抽取1个球,白颜色的球被抽到的可能性是,那么添加的球是
.
13.从一副扑克牌中任意抽取1张.
①这张牌是“A”;
②这张牌是“红桃”;
③这张牌是“大王”;
④这张牌是“红色的”.
将这些事件按发生的可能性从小到大顺序排列
.(填序号,用“<”连接)
14.一个小球在如图所示的地面上自由滚动,并随机地停留在某块方砖上,则小球停留在黑色区域的概率是
.
15.在一所有1500名学生的中学里,调查人员随机调查了50名学生,其中有40人每天都喝牛奶,那么在这所学校里,随便询问1人,每天都喝牛奶的概率是
.
16.小明与小颖用一副去掉大王和小王的扑克牌做摸牌游戏:小明从中任意摸一张牌(不放回),小颖从剩余的牌中任意摸一张,谁摸到的牌面大,谁就获胜(规定牌面从小到大的顺序为2,3,4,5,6,7,8,9,10,J,Q,K,A),然后两人把摸到的牌都放回,重新开始游戏,若小明已经摸到的牌面为4,然后小颖摸牌,那么小明获胜的概率是
.
17.欧阳修在《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”.如图所示,可见卖油翁的技艺之高超,若铜钱直径为4cm,中间有边长为1cm的正方形小孔,随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入口中的概率是
.
18.某景区为了解游客人数的变化规律,提高旅游服务质量,收集并整理了某月(30天)接待游客人数(单位:万人)的数据,绘制了下面的统计图和统计表.
每日接待游客人数(单位:万人)
游玩环境评价
0≤x<5
好
5≤x<10
一般
10≤x<15
拥挤
15≤x<20
严重拥挤
根据以上信息,以下四个判断中,正确的是
(填写所有正确结论的序号).
①该景区这个月游玩环境评价为“拥挤或严重拥挤”的天数仅有4天;
②该景区这个月每日接待游客人数的中位数在5~10万人之间;
③该景区这个月平均每日接待游客人数低于5万人;
④这个月1日至5日的五天中,如果某人曾经随机选择其中的两天到该景区游玩,那么他“这两天游玩环境评价均为好”的可能性为.
19.有四张不透明卡片,分别写有实数,﹣1,,,除正面的数不同外其余都相同,将它们背面朝上洗匀后,从中任取一张卡片,取到的数是无理数的可能性大小是
.
20.某校九年级(1)班计划开展“讲中国好故事”主题活动.第一小组的同学推荐了“北大红楼、脱贫攻坚、全面小康、南湖红船、抗疫精神、致敬英雄”六个主题,并将这六个主题分别写在六张完全相同的卡片上,然后将卡片放入不透明的口袋中.组长小东从口袋中随机抽取一张卡片,抽到含“红”字的主题卡片的概率是
.
三.解答题
21.下列事件:
(1)从装有1个红球和2个黄球的袋子中摸出的1个球是白球;
(2)随意调查1位青年,他接受过九年制义务教育;
(3)花2元买一张体育彩票,喜中500万大奖;
(4)抛掷1个小石块,石块会下落.
估计这些事件的可能性大小,在相应位置填上序号.
一定会发生的事件:
;
发生的可能性非常大的事件:
;
发生的可能性非常小的事件:
;
不可能发生的事件:
.
22.为庆祝中国共产党成立100周年,让红色基因、革命薪火代代传承,某校开展以学习“四史”(党史、新中国史、改革开放史、社会主义发展史)为主题的书画展,为了解作品主题分布情况,在学生上交的作品中,随机抽取了50份进行统计,并根据调查统计结果绘制了统计图表:主题
频数
频率
A党史
6
0.12
B新中国史
20
m
C改革开放史
0.18
D社会主义发展史
n
合计
50
1
请结合上述信息完成下列问题:
(1)m=
,n=
;
(2)请补全条形统计图;
(3)在扇形统计图中,“新中国史”主题作品份数对应的圆心角是
度;
(4)若该校同时开设两门课程,则开设课程B、C的概率为
.
23.如图是一个转盘.转盘分成8个相同的图形,颜色分为红、绿、黄三种.指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个图形的交线时,当作指向右边的图形).求下列事件的概率:
(1)指针指向红色;
(2)指针指向黄色或绿色.
24.“扫雷”是一个有趣的游戏,如图是此游戏的一部分:
图中数字2表示以该数字为中心的8个方格中有2个地雷,小旗表示该方格已被探明有地雷,现在还剩下A,B,C三个方格未被探明,其它地方为安全区(包括有数字的方格).试问:
(1)现在还剩下几个地雷?
(2)A,B,C三个方格中有地雷的概率分别是多少?
25.有两个盒子,分别装有若干个除颜色外都相同的球,第一个盒子装有4个红球和6个白球,第二个盒子装有6个红球和6个白球.分别从这两个盒子中各摸出1个球,请你通过计算来判断从哪一个盒子中摸出白球的可能性大.
26.一只不透明的袋子中装有1个白球、2个黄球和3个红球,每个球除颜色外都相同,将球摇匀,从中任意摸出一个球:
(1)该球是白球;
(2)该球是黄球;
(3)该球是红球.
估计上述事件发生的可能性的大小,将这些事件的序号按发生的可能性从小到大的顺序排列.
参考答案与试题解析
一.选择题
1.解:一副普通的54张的扑克牌中,①大王有一张;②小王有一张;③2有4张;④梅花有13张;
∵13>4>1,
∴这4个事件发生的可能性最大的是④.
故选:D.
2.解:根据题意可知:摸到红色球的可能性为=,
摸到白色球的可能性为=,
故摸到红色球的可能性大.
故选:A.
3.解:摸到白球的可能性为,摸到黄球的可能性为,摸到红球的可能性为,
所以摸到红球的可能性最大,
故选:A.
4.解:抛一枚质地均匀的硬币,有正面朝上、反面朝上两种结果,故正面朝上的概率=.
故选:B.
5.解:A、卡片上的数字是4的倍数的有4×1,4×2,4×3,4×4,4×5,共5张;
B、卡片上的数字是2的倍数2×1,2×2,2×3,2×4,2×5,2×6,2×7,2×8,2×9,2×10,共10张;
C、卡片上的数字是5的倍数5×1,5×2,5×3,5×4,共4张;
D、卡片上的数字是3的倍数3×1,3×2,3×3,3×4,3×5,3×6,共6张.
故选:B.
6.解:∵指针恰好指向白色扇形的穊率为,
∴黑、白两种颜色的扇形的面积比为1:7,
∴∠AOB=×360°=45°,
故选:B.
7.解:设第3根竹签长为xcm,
∵已有两根长度分别是3cm和6cm的细竹签,
∴第三根可以构成三角形的范围是:3<x<9,
其中4cm,7cm,8cm符合题意,
则小明从盒子里随意抽取一根细竹签,恰能与已有的两根细竹签首尾顺次联结组成三角形的概率是:.
故选:C.
8.解:∵AD:DB=1:2,DE∥BC,
∴AE:EC=1:2,
∵FE∥BA,
∴CF:BF=2:1,
∴△BDF的面积=××△ABC的面积=×△ABC的面积,
△ADE的面积=××△ABC的面积=×△ABC的面积,
△BDF的面积=××△ABC的面积=×△ABC的面积,
∴△DEF(阴影)区域内的面积=×△ABC的面积,
∴针扎到△DEF(阴影)区域内的概率是÷1=.
故选:B.
9.解:∵某十字路口的交通信号灯,红灯亮50秒,绿灯亮40秒,黄灯亮10秒,
∴当你抬头看信号灯时,是红灯的概率为:=
故选:A.
10.解:A、袋子中装有4个黑球和2个白球,摸出的三个球中可能为两个白球一个黑球,
∴3个都是黑球的概率小于1;
B、袋子中有4个黑球,有可能摸到的全部是黑球,B有可能不发生,
∴2个黑球1个白球的概率小于1;
C、袋子中有4个黑球,有可能摸到的全部是黑球,C有可能不发生,
∴2个白球1个黑球的概率小于1;
D、白球只有两个,如果摸到三个球不可能都是白梂,因此至少有一个是黑球,
∴至少有1个黑球的概率为1,
故选:D.
二.填空题
11.解:从一副扑克牌中任意抽取一张,
(1)这张牌是“A”的概率为=;
(2)这张牌是“红心”的概率为;
(3)这张牌是“大王”的概率为;
(4)这张牌是“红色的”的概率为=,
∴(3)<(1)<(2)<(4),
故答案为:(3)<(1)<(2)<(4).
12.解:∵2÷(2+2+1)=,
∴原来白颜色的球被抽到的可能性是;
∵>,
∴添加的球是红球或黄球.
故答案为:红球或黄球.
13.解:一副扑克牌中含“A”4张,“红桃”13张,“大王”1张,“红色的”26张,
∵1<4<13<26,
∴将这些事件按发生的可能性从小到大顺序排列:③①②④.
故答案为:③①②④.
14.解:由图可知:黑色区域在整个地面中所占的比值=,
∴小球最终停留在黑色区域的概率=,
故答案为:.
15.解:在这所学校里,随便询问1人,每天都喝牛奶的概率是=,
故答案为:.
16.解:由题意知,去掉大王、小王的扑克牌共有52张,其中比4小的牌有2,3,
∴小明获胜的概率是=,
故答案为:.
17.解:∵直径为4cm的铜钱的面积=π×22=4π,边长为1cm的正方形小孔的面积=1×1=1,
∴随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入口中的概率=;
故答案为:.
18.解:①根据题意每日接待游客人数10≤x<15为拥挤,15≤x<20为严重拥挤,
由统计图可知,游玩环境评价为“拥挤或严重拥挤”,1日至5日有1天,25日﹣30日有3天,共4天,故①正确;
②本题中位数是指将30天的游客人数从小到大排列,第15与第16位的和除以2,
根据统计图可知0≤x<5的有16天,从而中位数位于0≤x<5范围内,故②错误;
③从统计图可以看出,接近10的有6天,大于10而小于15的有2天,15以上的有2天,
10上下的估算为10,则(10×8+15×2﹣5×10)÷16=3.25,
可以考虑为给每个0至5的补上3.25,则大部分大于5,而0至5范围内有6天接近5,故平均数一定大于5,故③错误;
④由题意可知“这两天游玩环境评价均为好”的可能性为:×=,故④正确.
故答案为:①④.
19.解:∵实数,﹣1,,中,,是无限不循环小数,
∴无理数有2个,
∴取到的数是无理数的可能性大小是:
2÷4=.
故答案为:.
20.解:含“红”字的主题卡片有“北大红楼”和“南湖红船”共2张,
所以抽到含“红”字的主题卡片的概率是.
故答案为:.
三.解答题
21.解:(1)从装有1个红球和2个黄球的袋子中摸出的1个球是白球的概率是0,不可能发生;
(2)随意调查1位青年,他接受过九年制义务教育概率较大,发生的可能性较大;
(3)花2元买一张体育彩票,喜中500万大奖,概率较小,发生的可能性较小;
(4)抛掷1个小石块,石块会下落,概率为1,一定会发生.
故答案为:(4);(2);(3);(1).
22.解:(1)由统计图表可知:
m==0.4,
∴n=1﹣0.12﹣0.18﹣0.4=0.3,
故m=0.4,n=0.3;
(2)结果如下:
(3)∵新中国史的频率为0.4,
∴360°×0.4=144°,
∴“新中国史”主题作品份数对应的圆心角是144°;
(4)列表如下:
∴一共有12种情况,开设课程B,C的有2种情况,
∴开设课程B、C的概率为:P=.
23.解:按颜色把8个扇形分为红1、红2、绿1、绿2、绿3、黄1、黄2、黄3,所有可能结果的总数为8,
(1)指针指向红色的结果有2个,
∴P(指针指向红色)=;
(2)指针指向黄色或绿色的结果有3+3=6个,
∴P(指针指向黄色或绿色)==.
24.解:(1)∵于B、C下面标2,说明它们为中心的8个方格中有2个地雷,而C的右边已经有一个,
∴A就是一个地雷,还有一个可能在B、C的位置,
∴现在还剩下2个地雷;
(2)根据(1)得
P(A有地雷)=1,
P(B有地雷)=,
P(C有地雷)=.
25.解:P(从第一个盒子中摸出一个白球)=,
P(从第二个盒子中摸出一个白球)=,
∵,
∴第一个盒子中摸到白球的可能性大.
26.解:∵不透明的袋子中装有1个白球、2个黄球和3个红球,
∴摸到白球的概率为,
摸到黄球的概率为=,
摸到红球的概率为=,
∵,
∴(1)<(2)<(3).
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
