人教版八年级上册12.2 全等三角形的判定第4课时 “斜边、直角边” 课件(共20张PPT)
文档属性
| 名称 | 人教版八年级上册12.2 全等三角形的判定第4课时 “斜边、直角边” 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
12.2
全等三角形的判定
第4课时
“斜边、直角边”
教学目标
1.经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
2.掌握直角三角形全等的条件,并能运用其解决一些实际问题.
复习导入
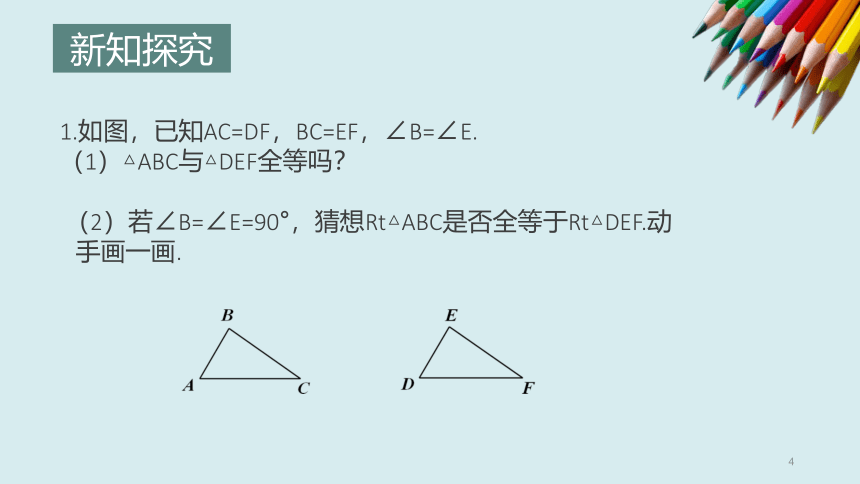
1.我们学过的判定三角形全等的方法有______________.
2.如图,AB⊥BE于C,DE⊥BE于E,
(1)若∠A=∠D,AB=DE,则△ABC与△DEF
(填“全等”或“不全等”
),根据
(用简写法);
(2)若∠A=∠D,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”
),根据
(用简写法);
(3)若AB=DE,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”
),根据
(用简写法).
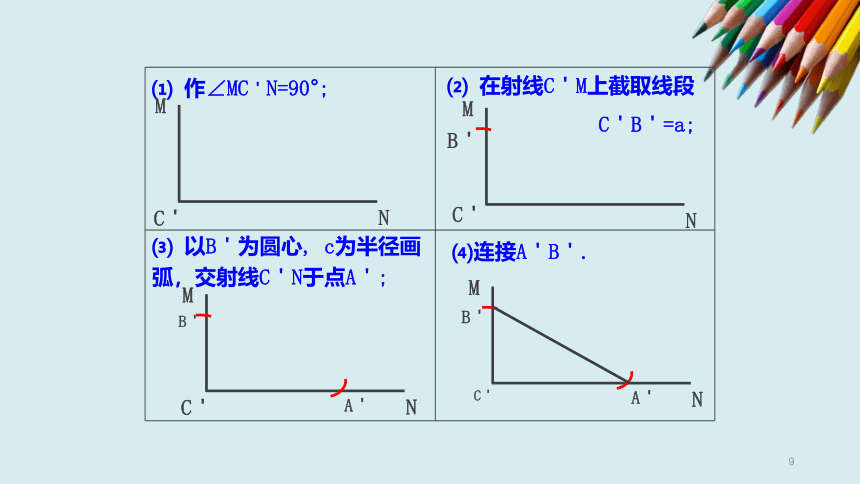
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A
′
B′
C
′
在Rt△ABC和Rt△
A′B′C′
中,
∴Rt△ABC
≌
Rt△
A′B′C′
(HL).
AB=A′B′,
BC=B′C′,
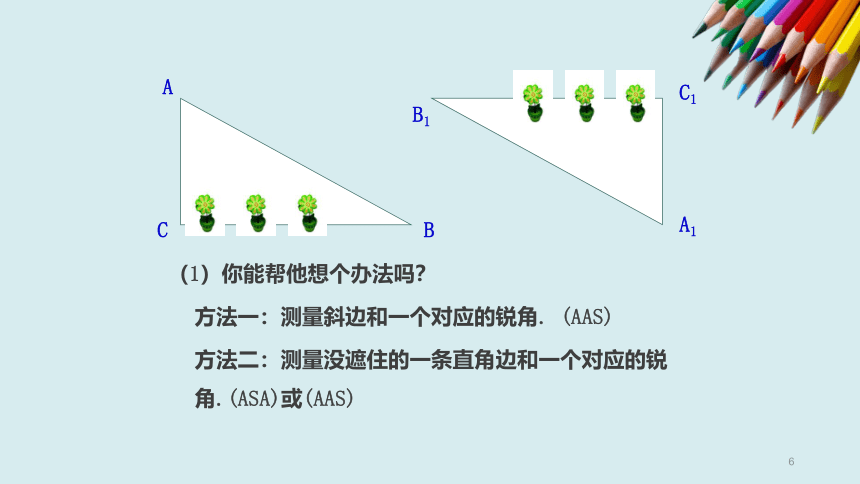
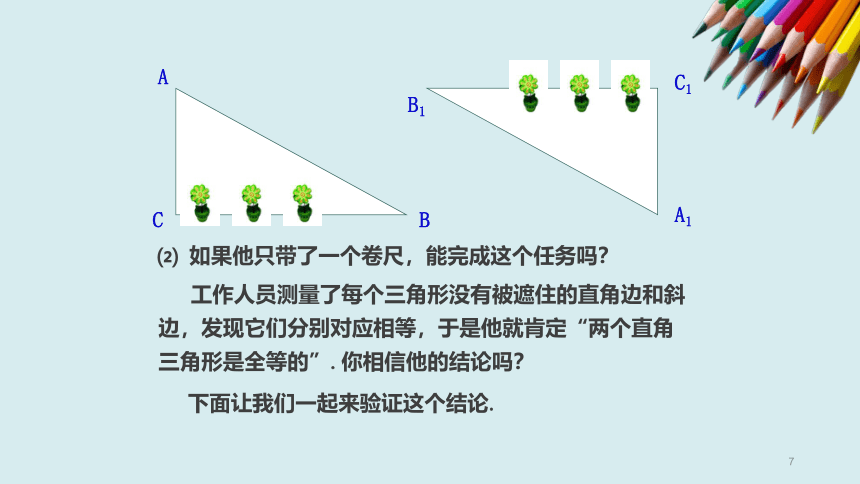
“斜边、直角边”判定方法
判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等;(
)
(2)一个锐角和这个角的邻边对应相等;(
)
(3)一个锐角和斜边对应相等;
(
)
(4)两直角边对应相等;
(
)
(5)一条直角边和斜边对应相等.
(
)
HL
×
SAS
AAS
AAS
判一判
例1
如图,AC⊥BC,
BD⊥AD,
AC﹦BD,求证:BC﹦AD.
证明:
∵
AC⊥BC,
BD⊥AD,
∴∠C与∠D都是直角.
AB=BA,
AC=BD
.
在
Rt△ABC
和Rt△BAD
中,
∴
Rt△ABC≌Rt△BAD
(HL).
∴
BC﹦AD.
A
B
D
C
变式1:
如图,
∠ACB
=∠ADB=90,要证明△ABC≌
△BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由.
(1)
(
)
(2)
(
)
(3)
(
)
(4)
(
)
A
B
D
C
AD=BC
∠
DAB=
∠
CBA
BD=AC
∠
DBA=
∠
CAB
HL
HL
AAS
AAS
4.如图,在△ABC中,已知BD⊥AC,CE
⊥AB,BD=CE.求证:△EBC≌△DCB.
A
B
C
E
D
证明:
∵
BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90
°.
在
Rt△EBC
和Rt△DCB
中,
CE=BD,
BC=CB
.
∴
Rt△EBC≌Rt△DCB
(HL).
3.如图,△ABC中,AB=AC,AD是高,则△ADB与△ADC
(填“全等”或“不全等”),根据
(用简写法).
全等
HL
A
F
C
E
D
B
5.如图,AB=CD,
BF⊥AC,DE⊥AC,AE=CF.
求证:BF=DE.
证明:
∵
BF⊥AC,DE⊥AC,
∴∠BFA=∠DEC=90
°.
∵AE=CF,
∴AE+EF=CF+EF.
即AF=CE.
在Rt△ABF和Rt△CDE中,
AB=CD,
AF=CE.
∴
Rt△ABF≌Rt△CDE(HL).
∴BF=DE.
课堂小结
直角三角形是特殊的三角形,所以不仅有一般三角形
判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形
特殊的判定方法:HL.
12.2
全等三角形的判定
第4课时
“斜边、直角边”
教学目标
1.经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
2.掌握直角三角形全等的条件,并能运用其解决一些实际问题.
复习导入
1.我们学过的判定三角形全等的方法有______________.
2.如图,AB⊥BE于C,DE⊥BE于E,
(1)若∠A=∠D,AB=DE,则△ABC与△DEF
(填“全等”或“不全等”
),根据
(用简写法);
(2)若∠A=∠D,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”
),根据
(用简写法);
(3)若AB=DE,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”
),根据
(用简写法).
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A
′
B′
C
′
在Rt△ABC和Rt△
A′B′C′
中,
∴Rt△ABC
≌
Rt△
A′B′C′
(HL).
AB=A′B′,
BC=B′C′,
“斜边、直角边”判定方法
判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等;(
)
(2)一个锐角和这个角的邻边对应相等;(
)
(3)一个锐角和斜边对应相等;
(
)
(4)两直角边对应相等;
(
)
(5)一条直角边和斜边对应相等.
(
)
HL
×
SAS
AAS
AAS
判一判
例1
如图,AC⊥BC,
BD⊥AD,
AC﹦BD,求证:BC﹦AD.
证明:
∵
AC⊥BC,
BD⊥AD,
∴∠C与∠D都是直角.
AB=BA,
AC=BD
.
在
Rt△ABC
和Rt△BAD
中,
∴
Rt△ABC≌Rt△BAD
(HL).
∴
BC﹦AD.
A
B
D
C
变式1:
如图,
∠ACB
=∠ADB=90,要证明△ABC≌
△BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由.
(1)
(
)
(2)
(
)
(3)
(
)
(4)
(
)
A
B
D
C
AD=BC
∠
DAB=
∠
CBA
BD=AC
∠
DBA=
∠
CAB
HL
HL
AAS
AAS
4.如图,在△ABC中,已知BD⊥AC,CE
⊥AB,BD=CE.求证:△EBC≌△DCB.
A
B
C
E
D
证明:
∵
BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90
°.
在
Rt△EBC
和Rt△DCB
中,
CE=BD,
BC=CB
.
∴
Rt△EBC≌Rt△DCB
(HL).
3.如图,△ABC中,AB=AC,AD是高,则△ADB与△ADC
(填“全等”或“不全等”),根据
(用简写法).
全等
HL
A
F
C
E
D
B
5.如图,AB=CD,
BF⊥AC,DE⊥AC,AE=CF.
求证:BF=DE.
证明:
∵
BF⊥AC,DE⊥AC,
∴∠BFA=∠DEC=90
°.
∵AE=CF,
∴AE+EF=CF+EF.
即AF=CE.
在Rt△ABF和Rt△CDE中,
AB=CD,
AF=CE.
∴
Rt△ABF≌Rt△CDE(HL).
∴BF=DE.
课堂小结
直角三角形是特殊的三角形,所以不仅有一般三角形
判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形
特殊的判定方法:HL.
