2.4 解直角三角形 同步培优提升专题训练 2021-2022学年鲁教版(五四制)九年级数学上册(Word版 含解析)
文档属性
| 名称 | 2.4 解直角三角形 同步培优提升专题训练 2021-2022学年鲁教版(五四制)九年级数学上册(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 407.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览



文档简介
2021年鲁教版九年级数学上册《2.4解直角三角形》同步培优提升专题训练(附答案)
一、选择题
1.如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
A.
B.
C.
D.
2.如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则cos∠CAB的值是( )
A.
B.
C.2
D.
3.如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则sin∠BAC的值为( )
A.
B.
C.
D.
4.如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则sin∠ACB的值为( )
A.
B.
C.
D.无法求得
5.如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为( )
A.
B.
C.
D.
6.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是AB边上的中线,AD=3,CE=5,则tan∠BCE的值为( )
A.
B.
C.
D.
7.如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A.
B.2
C.
D.
8.△ABC中,若AB=6,BC=8,∠B=120°,则△ABC的面积为( )
A.
B.12
C.
D.
9.如图,△ABC中,cosB=,sinC=,AC=5,则△ABC的面积是( )
A.
B.12
C.14
D.21
10.如图,在菱形ABCD中,DE⊥AB,,BE=2,则tan∠DBE的值( )
A.
B.2
C.
D.
11.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=,则AD的长为( )
A.2
B.
C.
D.1
二、非选择题
12.如图,在直角△BAD中,延长斜边BD到点C,使DC=BD,连接AC,若tanB=,则tan∠CAD的值
.
13.如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求sinC的值.
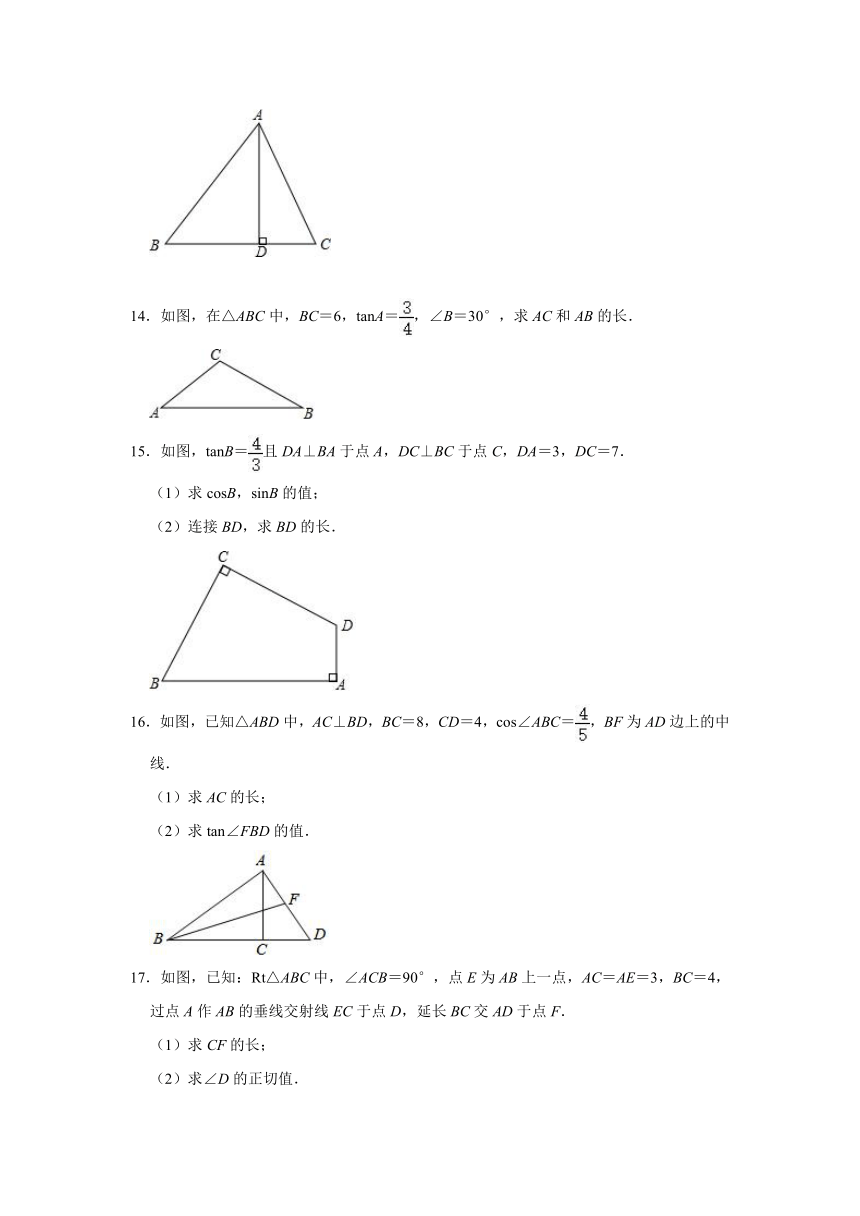
14.如图,在△ABC中,BC=6,tanA=,∠B=30°,求AC和AB的长.
15.如图,tanB=且DA⊥BA于点A,DC⊥BC于点C,DA=3,DC=7.
(1)求cosB,sinB的值;
(2)连接BD,求BD的长.
16.如图,已知△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
(2)求tan∠FBD的值.
17.如图,已知:Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.
(1)求CF的长;
(2)求∠D的正切值.
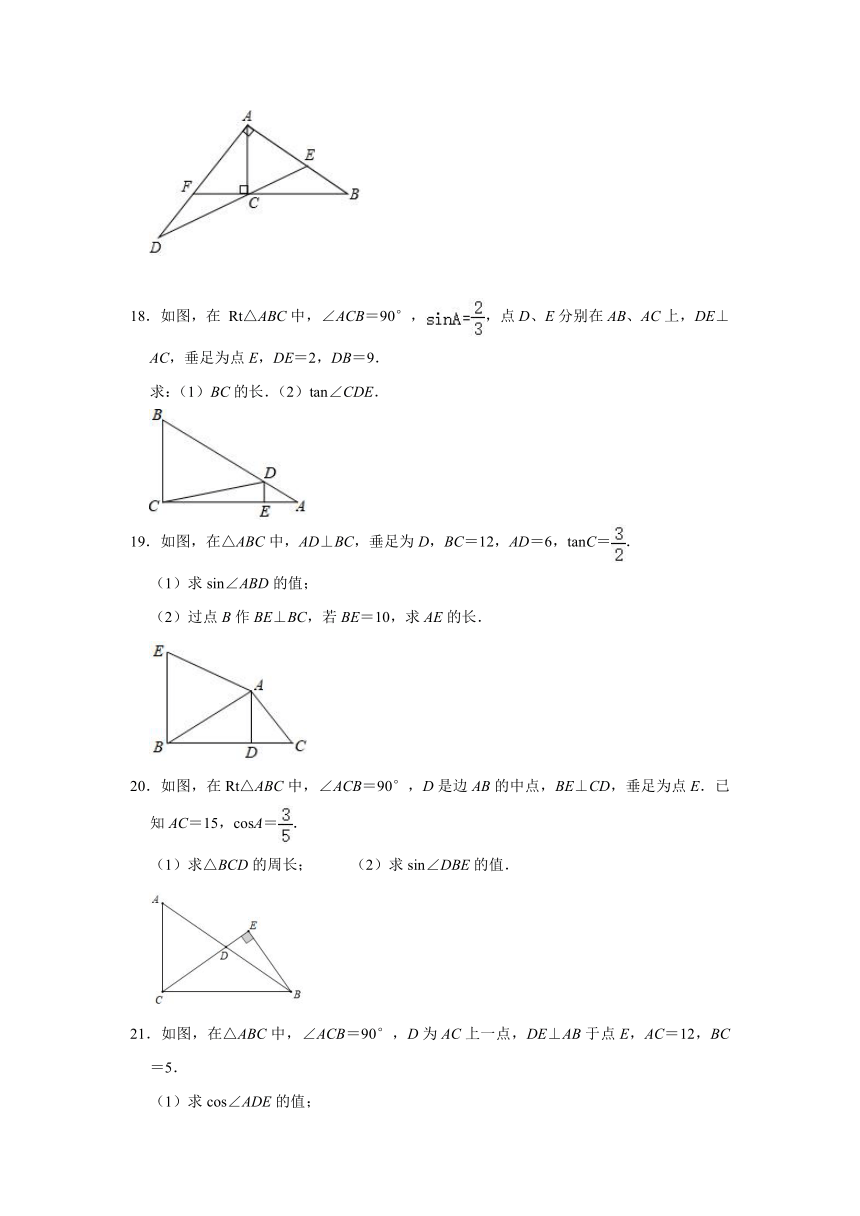
18.如图,在
Rt△ABC中,∠ACB=90°,,点D、E分别在AB、AC上,DE⊥AC,垂足为点E,DE=2,DB=9.
求:(1)BC的长.(2)tan∠CDE.
19.如图,在△ABC中,AD⊥BC,垂足为D,BC=12,AD=6,tanC=.
(1)求sin∠ABD的值;
(2)过点B作BE⊥BC,若BE=10,求AE的长.
20.如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cosA=.
(1)求△BCD的周长;
(2)求sin∠DBE的值.
21.如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
参考答案
1.解:作PA⊥x轴于A,如右图.
∵P(3,4),
∴OA=3,AP=4,
∴OP==5,
∴sinα=.
故选:D.
2.解:取格点D,E,连接BD,如图,
∵∠CDE=∠BDE=45°,
∴∠CDB=90°.
∵AD=,AB=,
∴在Rt△ADB中,cos∠CAB=.
故选:B.
3.解:过B作BH⊥AC于H,
∵S△ABC=BC?AD=AC?BH,
∴BH==,
∴sin∠BAC===,
故选:B.
4.解:作AD⊥BC于点D,
由每个小正方形边长为1,
故AC=BC==,
由三角形等面积法可得:
=,
即2×3=,
∴AD==,
∴sin∠ACB===.
故选:B.
5.解:连接BF,
∵CE是斜边AB上的中线,EF⊥AB,
∴EF是AB的垂直平分线,
∴S△AFE=S△BFE=5,∠FBA=∠A,
∴S△AFB=10=AF?BC,
∵BC=4,
∴AF=5=BF,
在Rt△BCF中,BC=4,BF=5,
∴CF==3,
∵CE=AE=BE=AB,
∴∠A=∠FBA=∠ACE,
又∵∠BCA=90°=∠BEF,
∴∠CBF=90°﹣∠BFC=90°﹣2∠A,
∠CEF=90°﹣∠BEC=90°﹣2∠A,
∴∠CEF=∠FBC,
∴sin∠CEF=sin∠FBC==,
故选:A.
6.解:∵CE是AB边上的中线,CE=5,
∴AE=BE=5,AB=10,
∴∠BCE=∠EBC,
∵AD=3,
∴BD=AB﹣AD=7,DE=AE﹣AD=2,
在Rt△CDE中,由勾股定理得:
CD===,
∴tan∠BCE=tan∠EBC==.
故选:B.
7.解:如图:
作OF⊥AB于F,
∵AB=AC,AD平分∠BAC.
∴∠ODB=90°.BD=CD=6.
∴根据勾股定理得:AD==8.
∵BE平分∠ABC.
∴OF=OD,BF=BD=6,AF=10﹣6=4.
设OD=OF=x,则AO=8﹣x,在Rt△AOF中,根据勾股定理得:
(8﹣x)2=x2+42.
∴x=3.
∴OD=3.
在Rt△OBD中,tan∠OBD===.
故选:A.
8.解:作AD⊥BC于点D.
∵∠B=120°,
∴∠ABD=180°﹣120°=60°,
在直角△ABD中,AD=AB?sin60°=6×=3,
在△ABC的面积是:BC?AD=×8×3=12.
故选:A.
9.解:过点A作AD⊥BC,
∵△ABC中,cosB=,sinC=,AC=5,
∴cosB==,
∴∠B=45°,
∵sinC===,
∴AD=3,
∴CD==4,
∴BD=3,
则△ABC的面积是:×AD×BC=×3×(3+4)=.
故选:A.
10.解:设菱形ABCD边长为t.
∵BE=2,
∴AE=t﹣2.
∵cosA=,
∴.
∴=.
∴t=5.
∴AE=5﹣2=3.
∴DE==4.
∴tan∠DBE===2.
故选:B.
11.解:作DE⊥AB于E,如图,
∵∠C=90°,AC=BC=6,
∴△ACB为等腰直角三角形,AB=AC=6,
∴∠A=45°,
在Rt△ADE中,设AE=x,则DE=x,AD=x,
在Rt△BED中,tan∠DBE==,
∴BE=5x,
∴x+5x=6,解得x=,
∴AD=×=2.
故选:A.
12.解:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,即=,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴===,
∴CE=x,DE=x,
∴AE=,
∴tan∠CAD==,
故答案为.
13.解:∵AD⊥BC,∴∠ADB=90°,
在Rt△ABD中,tan∠BAD==,
∴BD=ADtan∠BAD=9,
∵BC=14,
∴CD=BC﹣BD=5,
∴AC==13,
∴sinC==.
14.解:如图,过点C作CD⊥AB于点D,
在Rt△BCD中,sinB=sin30°==.
∴CD=×6=3,
BD===3
在Rt△ACD中,
tanA==,
∴AD==4.
AC=
=
=5
∴AB=AD+BD
=4+3.
15.解:(1)延长CD,BA,它们相交于点E,如图,
∵DC⊥BC于点C,
∴∠BCE=90°.
∵tanB=,tanB=,
∴.
设CE=4k,则BC=3k.
∴BE=.
∴cosB=.
sinB=.
(2)如下图:
∵DA⊥BA于点A,
∴∠E+∠ADE=90°.
∵DC⊥BC于点C,
∴∠E+∠CBE=90°.
∴∠ADE=∠CBE.
∴cos∠ADE=cos∠CBE=.
∵cos∠ADE=,
∴.
∵AD=3,
∴DE=5.
∴CE=CD+DE=5+7=12.
∵tan∠CBE=,tan∠CBE=,
∴.
∴BC=9.
∴BD=.
16.解:(1)∵AC⊥BD,cos∠ABC==,BC=8,
∴AB=10,
在Rt△ACB中,由勾股定理得,
AC===6,
即AC的长为6;
(2)如图,
连接CF,过F点作BD的垂线,垂足E,
∵BF为AD边上的中线,
即F为AD的中点,
∴CF=AD=FD,
在Rt△ACD中,由勾股定理得,
AD===2,
∵三角形CFD为等腰三角形,FE⊥CD,
∴CE=CD=2,
在Rt△EFC中,EF===3,
∴tan∠FBD===.
解法二:EF直接用三角形中位线定理求解即可.
17.解:(1)∵∠ACB=90°,
∴∠ACF=∠ACB=90°,∠B+∠BAC=90°,
∵AD⊥AB,
∴∠BAC+∠CAF=90°,
∴∠B=∠CAF,
∴△ABC∽△FAC,
∴=,即=,
解得CF=;
(2)如图,过点C作CH⊥AB于点H,
∵AC=3,BC=4,
∴AB=5,
则CH==,
∴AH==,EH=AE﹣AH=,
∴tanD=tan∠ECH==.
18.解:(1)在Rt△DEA中,
∵DE=2,sinA=,
∴AD===3,
∵DB=9,
∴AB=BD+AD=12,
在Rt△ABC中,AB=12,sinA=,
∴BC=AB?sinA=12×=8;
(2)∵在Rt△ABC中,AB=12,BC=8,
∴AC==4,
∵在Rt△DEA中,DE=2,AD=3,
∴AE==,
∴CE=AC﹣AE=3,
∴tan∠CDE==.
19.解:(1)∵tanC===,
∴CD=4,BD=BC﹣CD=12﹣4=8,
∴AB===10,
∴sin∠ABD===.
(2)过点A作AF⊥BE于点F,如图.
∵∠AFB=∠FBD=∠ADB=90°,
∴四边形FBDA为矩形,AF∥BD,AF=BD=8,BF=AD=6,
∴EF=BE﹣BF=10﹣6=4,
在Rt△AEF中,AE===.
20.解:(1)∵AC=15,cosA=,
∴cosA==,
∴AB=25,
∴BC===20,
∵△ACB为直角三角形,D是边AB的中点,
∴CD=,
∴△BCD的周长=25+20=45;
(2)∵AC=15,AB=25,BC=20,
∴cos∠ABC==,
∵DC=DB,
∴∠DCB=∠ABC,
∴cos∠DCB=cos∠ABC=,
∵BE⊥CD,
∴∠BEC=90°,
∴cos∠DCB=,
即=,
∴CE=16,
∴DE=CE﹣CD=16﹣12.5=3.5,
∴sin∠DBE===.
21.解:(1)∵DE⊥AB,
∴∠DEA=90°,
∴∠A+∠ADE=90°,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠ADE=∠B,
在Rt△ABC中,∵AC=12,BC=5,
∴AB=13,
∴,
∴;
(2)由(1)得,
设AD为x,则,
∵AC=AD+CD=12,
∴,
解得,
∴.
一、选择题
1.如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
A.
B.
C.
D.
2.如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则cos∠CAB的值是( )
A.
B.
C.2
D.
3.如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则sin∠BAC的值为( )
A.
B.
C.
D.
4.如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则sin∠ACB的值为( )
A.
B.
C.
D.无法求得
5.如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为( )
A.
B.
C.
D.
6.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是AB边上的中线,AD=3,CE=5,则tan∠BCE的值为( )
A.
B.
C.
D.
7.如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A.
B.2
C.
D.
8.△ABC中,若AB=6,BC=8,∠B=120°,则△ABC的面积为( )
A.
B.12
C.
D.
9.如图,△ABC中,cosB=,sinC=,AC=5,则△ABC的面积是( )
A.
B.12
C.14
D.21
10.如图,在菱形ABCD中,DE⊥AB,,BE=2,则tan∠DBE的值( )
A.
B.2
C.
D.
11.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=,则AD的长为( )
A.2
B.
C.
D.1
二、非选择题
12.如图,在直角△BAD中,延长斜边BD到点C,使DC=BD,连接AC,若tanB=,则tan∠CAD的值
.
13.如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求sinC的值.
14.如图,在△ABC中,BC=6,tanA=,∠B=30°,求AC和AB的长.
15.如图,tanB=且DA⊥BA于点A,DC⊥BC于点C,DA=3,DC=7.
(1)求cosB,sinB的值;
(2)连接BD,求BD的长.
16.如图,已知△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
(2)求tan∠FBD的值.
17.如图,已知:Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.
(1)求CF的长;
(2)求∠D的正切值.
18.如图,在
Rt△ABC中,∠ACB=90°,,点D、E分别在AB、AC上,DE⊥AC,垂足为点E,DE=2,DB=9.
求:(1)BC的长.(2)tan∠CDE.
19.如图,在△ABC中,AD⊥BC,垂足为D,BC=12,AD=6,tanC=.
(1)求sin∠ABD的值;
(2)过点B作BE⊥BC,若BE=10,求AE的长.
20.如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cosA=.
(1)求△BCD的周长;
(2)求sin∠DBE的值.
21.如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
参考答案
1.解:作PA⊥x轴于A,如右图.
∵P(3,4),
∴OA=3,AP=4,
∴OP==5,
∴sinα=.
故选:D.
2.解:取格点D,E,连接BD,如图,
∵∠CDE=∠BDE=45°,
∴∠CDB=90°.
∵AD=,AB=,
∴在Rt△ADB中,cos∠CAB=.
故选:B.
3.解:过B作BH⊥AC于H,
∵S△ABC=BC?AD=AC?BH,
∴BH==,
∴sin∠BAC===,
故选:B.
4.解:作AD⊥BC于点D,
由每个小正方形边长为1,
故AC=BC==,
由三角形等面积法可得:
=,
即2×3=,
∴AD==,
∴sin∠ACB===.
故选:B.
5.解:连接BF,
∵CE是斜边AB上的中线,EF⊥AB,
∴EF是AB的垂直平分线,
∴S△AFE=S△BFE=5,∠FBA=∠A,
∴S△AFB=10=AF?BC,
∵BC=4,
∴AF=5=BF,
在Rt△BCF中,BC=4,BF=5,
∴CF==3,
∵CE=AE=BE=AB,
∴∠A=∠FBA=∠ACE,
又∵∠BCA=90°=∠BEF,
∴∠CBF=90°﹣∠BFC=90°﹣2∠A,
∠CEF=90°﹣∠BEC=90°﹣2∠A,
∴∠CEF=∠FBC,
∴sin∠CEF=sin∠FBC==,
故选:A.
6.解:∵CE是AB边上的中线,CE=5,
∴AE=BE=5,AB=10,
∴∠BCE=∠EBC,
∵AD=3,
∴BD=AB﹣AD=7,DE=AE﹣AD=2,
在Rt△CDE中,由勾股定理得:
CD===,
∴tan∠BCE=tan∠EBC==.
故选:B.
7.解:如图:
作OF⊥AB于F,
∵AB=AC,AD平分∠BAC.
∴∠ODB=90°.BD=CD=6.
∴根据勾股定理得:AD==8.
∵BE平分∠ABC.
∴OF=OD,BF=BD=6,AF=10﹣6=4.
设OD=OF=x,则AO=8﹣x,在Rt△AOF中,根据勾股定理得:
(8﹣x)2=x2+42.
∴x=3.
∴OD=3.
在Rt△OBD中,tan∠OBD===.
故选:A.
8.解:作AD⊥BC于点D.
∵∠B=120°,
∴∠ABD=180°﹣120°=60°,
在直角△ABD中,AD=AB?sin60°=6×=3,
在△ABC的面积是:BC?AD=×8×3=12.
故选:A.
9.解:过点A作AD⊥BC,
∵△ABC中,cosB=,sinC=,AC=5,
∴cosB==,
∴∠B=45°,
∵sinC===,
∴AD=3,
∴CD==4,
∴BD=3,
则△ABC的面积是:×AD×BC=×3×(3+4)=.
故选:A.
10.解:设菱形ABCD边长为t.
∵BE=2,
∴AE=t﹣2.
∵cosA=,
∴.
∴=.
∴t=5.
∴AE=5﹣2=3.
∴DE==4.
∴tan∠DBE===2.
故选:B.
11.解:作DE⊥AB于E,如图,
∵∠C=90°,AC=BC=6,
∴△ACB为等腰直角三角形,AB=AC=6,
∴∠A=45°,
在Rt△ADE中,设AE=x,则DE=x,AD=x,
在Rt△BED中,tan∠DBE==,
∴BE=5x,
∴x+5x=6,解得x=,
∴AD=×=2.
故选:A.
12.解:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,即=,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴===,
∴CE=x,DE=x,
∴AE=,
∴tan∠CAD==,
故答案为.
13.解:∵AD⊥BC,∴∠ADB=90°,
在Rt△ABD中,tan∠BAD==,
∴BD=ADtan∠BAD=9,
∵BC=14,
∴CD=BC﹣BD=5,
∴AC==13,
∴sinC==.
14.解:如图,过点C作CD⊥AB于点D,
在Rt△BCD中,sinB=sin30°==.
∴CD=×6=3,
BD===3
在Rt△ACD中,
tanA==,
∴AD==4.
AC=
=
=5
∴AB=AD+BD
=4+3.
15.解:(1)延长CD,BA,它们相交于点E,如图,
∵DC⊥BC于点C,
∴∠BCE=90°.
∵tanB=,tanB=,
∴.
设CE=4k,则BC=3k.
∴BE=.
∴cosB=.
sinB=.
(2)如下图:
∵DA⊥BA于点A,
∴∠E+∠ADE=90°.
∵DC⊥BC于点C,
∴∠E+∠CBE=90°.
∴∠ADE=∠CBE.
∴cos∠ADE=cos∠CBE=.
∵cos∠ADE=,
∴.
∵AD=3,
∴DE=5.
∴CE=CD+DE=5+7=12.
∵tan∠CBE=,tan∠CBE=,
∴.
∴BC=9.
∴BD=.
16.解:(1)∵AC⊥BD,cos∠ABC==,BC=8,
∴AB=10,
在Rt△ACB中,由勾股定理得,
AC===6,
即AC的长为6;
(2)如图,
连接CF,过F点作BD的垂线,垂足E,
∵BF为AD边上的中线,
即F为AD的中点,
∴CF=AD=FD,
在Rt△ACD中,由勾股定理得,
AD===2,
∵三角形CFD为等腰三角形,FE⊥CD,
∴CE=CD=2,
在Rt△EFC中,EF===3,
∴tan∠FBD===.
解法二:EF直接用三角形中位线定理求解即可.
17.解:(1)∵∠ACB=90°,
∴∠ACF=∠ACB=90°,∠B+∠BAC=90°,
∵AD⊥AB,
∴∠BAC+∠CAF=90°,
∴∠B=∠CAF,
∴△ABC∽△FAC,
∴=,即=,
解得CF=;
(2)如图,过点C作CH⊥AB于点H,
∵AC=3,BC=4,
∴AB=5,
则CH==,
∴AH==,EH=AE﹣AH=,
∴tanD=tan∠ECH==.
18.解:(1)在Rt△DEA中,
∵DE=2,sinA=,
∴AD===3,
∵DB=9,
∴AB=BD+AD=12,
在Rt△ABC中,AB=12,sinA=,
∴BC=AB?sinA=12×=8;
(2)∵在Rt△ABC中,AB=12,BC=8,
∴AC==4,
∵在Rt△DEA中,DE=2,AD=3,
∴AE==,
∴CE=AC﹣AE=3,
∴tan∠CDE==.
19.解:(1)∵tanC===,
∴CD=4,BD=BC﹣CD=12﹣4=8,
∴AB===10,
∴sin∠ABD===.
(2)过点A作AF⊥BE于点F,如图.
∵∠AFB=∠FBD=∠ADB=90°,
∴四边形FBDA为矩形,AF∥BD,AF=BD=8,BF=AD=6,
∴EF=BE﹣BF=10﹣6=4,
在Rt△AEF中,AE===.
20.解:(1)∵AC=15,cosA=,
∴cosA==,
∴AB=25,
∴BC===20,
∵△ACB为直角三角形,D是边AB的中点,
∴CD=,
∴△BCD的周长=25+20=45;
(2)∵AC=15,AB=25,BC=20,
∴cos∠ABC==,
∵DC=DB,
∴∠DCB=∠ABC,
∴cos∠DCB=cos∠ABC=,
∵BE⊥CD,
∴∠BEC=90°,
∴cos∠DCB=,
即=,
∴CE=16,
∴DE=CE﹣CD=16﹣12.5=3.5,
∴sin∠DBE===.
21.解:(1)∵DE⊥AB,
∴∠DEA=90°,
∴∠A+∠ADE=90°,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠ADE=∠B,
在Rt△ABC中,∵AC=12,BC=5,
∴AB=13,
∴,
∴;
(2)由(1)得,
设AD为x,则,
∵AC=AD+CD=12,
∴,
解得,
∴.
