2021-2022学年鲁教版(五四制)九年级数学上册2.5三角函数的应用 同步优生辅导训(word解析版)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学上册2.5三角函数的应用 同步优生辅导训(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 468.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览



文档简介
2021年鲁教版九年级数学上册《2.5三角函数的应用》同步优生辅导训练(附答案)
一.选择题(共15小题)
1.如图,电线杆的高度为CD=m,两根拉线AC与BC互相垂直(点A、点D、点B在同一条直线上),若∠CAB=α,则拉线BC的长度可以表示为( )
A.
B.
C.
D.mcosα
2.如图,要测量一条河两岸相对的两点A,B之间的距离,我们可以在岸边取点C和D,使点B,C,D共线且直线BD与AB垂直,测得∠ACB=56.3°,∠ADB=45°,CD=10m,则AB的长约为( )
(sin56.3°≈0.8,cos56.3°≈0.6,tan56.3°≈1.5,sin45°≈0.7,cos45°≈0.7,tan45=1)
A.15m
B.30m
C.35m
D.40m
3.如图,兴趣小组探究活动中,小明要测量小河两岸相对的两点P,A的距离,他和同学利用工具测得PC=50米,∠PCA=α,根据上述测量数据可计算小河宽度PA为( )
A.
米
B.50sinα米
C.
米
D.50tanα米
4.人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点.图2是它的示意图,AB=AC,BD=140cm,∠BAC=40°,则点D离地面的高度DE为( )
A.140sin20°cm
B.140cos20°cm
C.140sin40°cm
D.140cos40°cm
5.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点D到OB的距离等于( )
A.asinx+bsinx
B.acosx+bcosx
C.asinx+bcosx
D.acosx+bsinx
6.比萨斜塔是意大利的著名建筑,其示意图如图所示,设塔顶中心点为点B,塔身中心线AB与垂直中心线AC的夹角为∠A,过点B向垂直中心线AC引垂线,垂足为点D.通过测量可得AB、BD、AD的长度,利用测量所得的数据计算∠A的三角函数值,进而可求∠A的大小.下列关系式正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.sinA=
7.如图,传送带和地面所成斜坡的坡度i=1:2.4,如果它把某物体从地面送到离地面10米高的地方,那么该物体所经过的路程是( )
A.10米
B.24米
C.25米
D.26米
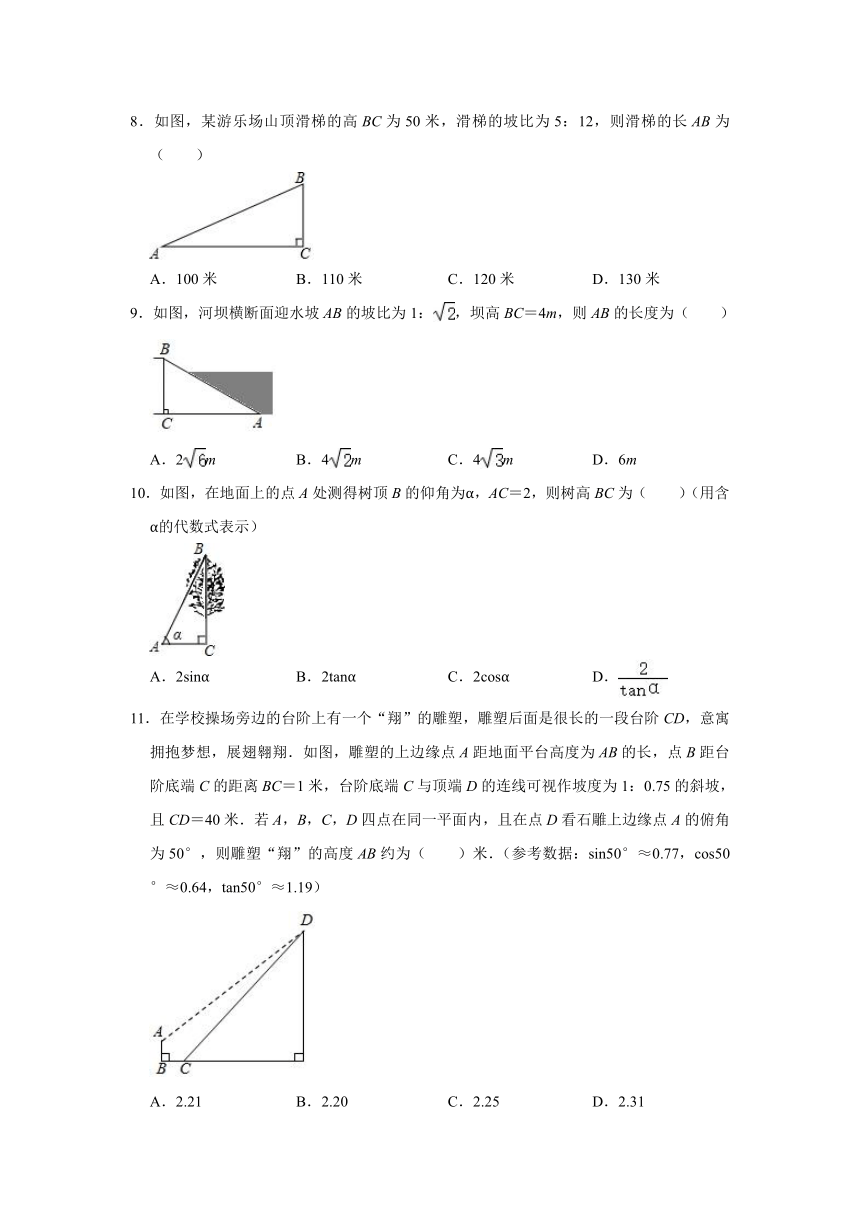
8.如图,某游乐场山顶滑梯的高BC为50米,滑梯的坡比为5:12,则滑梯的长AB为( )
A.100米
B.110米
C.120米
D.130米
9.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,则AB的长度为( )
A.2m
B.4m
C.4m
D.6m
10.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα
B.2tanα
C.2cosα
D.
11.在学校操场旁边的台阶上有一个“翔”的雕塑,雕塑后面是很长的一段台阶CD,意寓拥抱梦想,展翅翱翔.如图,雕塑的上边缘点A距地面平台高度为AB的长,点B距台阶底端C的距离BC=1米,台阶底端C与顶端D的连线可视作坡度为1:0.75的斜坡,且CD=40米.若A,B,C,D四点在同一平面内,且在点D看石雕上边缘点A的俯角为50°,则雕塑“翔”的高度AB约为( )米.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
A.2.21
B.2.20
C.2.25
D.2.31
12.某次暴雨来袭时,需要测量公路AB遇到塌方,运输车辆只能沿从坡度比为i=1:2.4斜坡AE将货物运输到山顶C处,运输车辆到达E处,测得仰角为36°,AE=260米,CE=110米,则山CD的高度为( ).(参考数据:sin36°≈0.6,cos36°≈0.8)
A.137
B.188
C.176
D.166
13.如图,一艘潜水艇在海面下300米的点A处发现其正前方的海底C处有黑匣子,同时测得黑匣子C的俯角为30°,潜水艇继续在同一深度直线航行960米到点B处,测得黑匣子C的俯角为60°,则黑匣子所在的C处距离海面的深度是( )
A.(480+300)米
B.(960+300)米
C.780米
D.1260米
14.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AD与AB的长度之比为( )
A.
B.
C.
D.
15.如果小丽在楼上点A处看到楼下点B处小明的俯角是35°,那么点B处小明看点A处小丽的仰角是( )
A.35°
B.45°
C.55°
D.65°
二.填空题(共8小题)
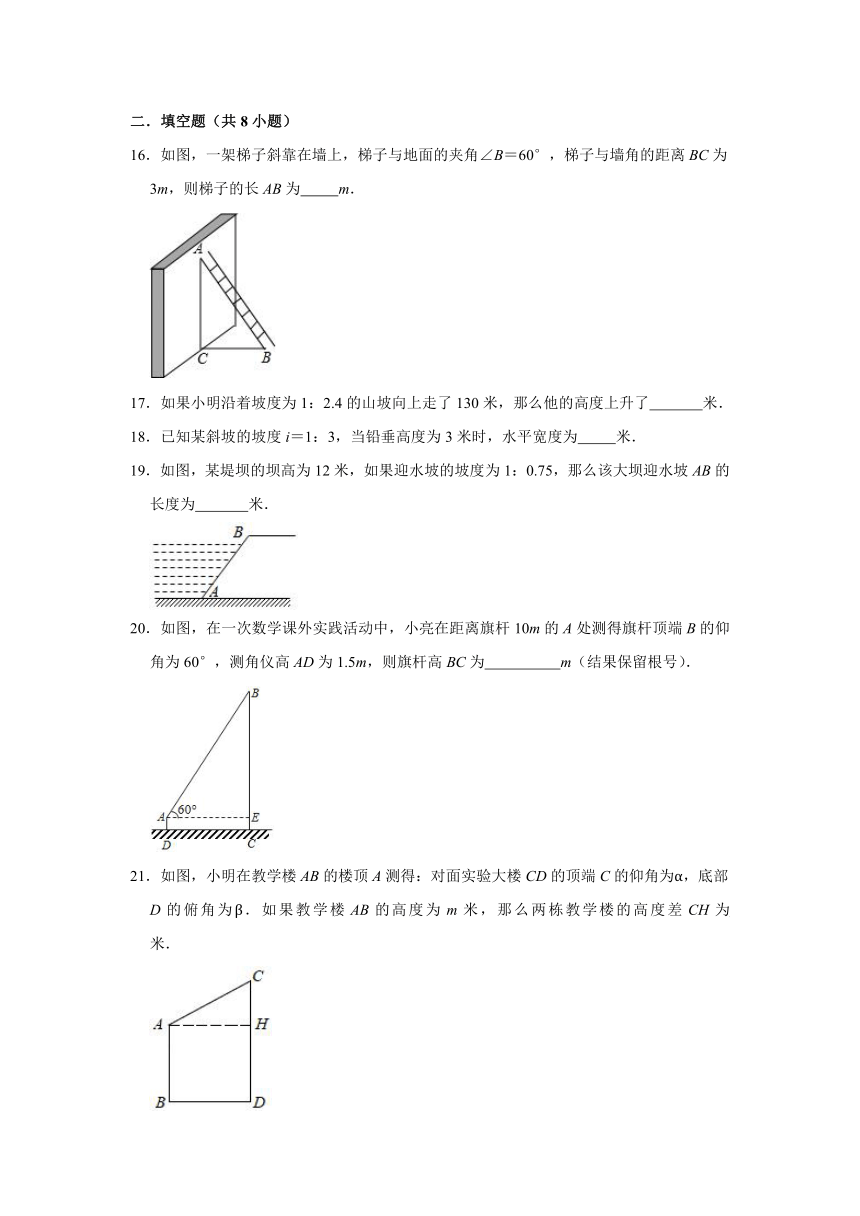
16.如图,一架梯子斜靠在墙上,梯子与地面的夹角∠B=60°,梯子与墙角的距离BC为3m,则梯子的长AB为
m.
17.如果小明沿着坡度为1:2.4的山坡向上走了130米,那么他的高度上升了
米.
18.已知某斜坡的坡度i=1:3,当铅垂高度为3米时,水平宽度为
米.
19.如图,某堤坝的坝高为12米,如果迎水坡的坡度为1:0.75,那么该大坝迎水坡AB的长度为
米.
20.如图,在一次数学课外实践活动中,小亮在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1.5m,则旗杆高BC为
m(结果保留根号).
21.如图,小明在教学楼AB的楼顶A测得:对面实验大楼CD的顶端C的仰角为α,底部D的俯角为β.如果教学楼AB的高度为m米,那么两栋教学楼的高度差CH为
米.
22.如图,小明想在自己家的窗口A处测量对面建筑物CD的高度,他首先量出窗口A到地面的距离AB为1.5m,又测得从A处看建筑物底部C的俯角为30°,看建筑物顶部D的仰角为45°,且AB,CD都与地面垂直,点A,B,C,D在同一平面内.则建筑物CD的高度
m.
23.高新一中初中校区九年级(一)班课外活动小组为了测得学校旗杆的高度,他们在离旗杆6米的A处,用高为1.5米的仪器测得旗杆顶部B处的仰角为60°,如图所示,则旗杆的高度为
米.(结果保留根号)
三.解答题(共7小题)
24.如图,为了测量河宽,在河的一边沿岸选取B、C两点,对岸岸边有一块石头A,在△ABC中,测得∠B=64°,∠C=45°,BC=50米,求河宽(即点A到边BC的距离)(结果精确到0.1米).
(参考数据:≈1.41,sin64°=0.90,cos64°=0.44,tan64°=2.05)
25.如图,修公路遇到一座山,于是要修一条隧道,为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过点C作直线AB的垂线l,过点B作一直线(在山的旁边经过),与l相交于D点,经测量∠ABD=135°,BD=800m,求直线l上距离D点多远的C处开挖?(≈1.414,精确到1米)
26.5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛峰完成峰顶测量任务,受此消息鼓舞,某数学小组开展了一次测量小山高度的活动,如图,该数学小组从地面A处出发,沿坡角为53°的山坡AB直线上行一段距离到达B处,再沿着坡角为22°的山坡BC直线上行600米到达C处,通过测量数据计算出小山高CD=500m.求该数学小组行进的水平距离AD(结果精确到1m).(参考数据:sin22°≈0.37,cos22°≈0.92,tan22°≈0.32,sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
27.如图,某商场门前的台阶高出地面0.8米,即CB=0.8米,现将此台阶改造成供轮椅行走的斜坡AC,并且设计斜坡的倾斜角∠A为10°.求斜坡AC的长.(结果精确到0.1m)
【参考数据:sin10°=0.17.cos10°=0.98,tan10°=0.18】
28.某中学门口新装了一批太阳能路灯,在路面A点观察点D的仰角为60°,观察点C的仰角为45°,灯管安装处D点与太阳能电池板安装处E点在同一水平线上,已知灯管支架CD长度为1.4米,且∠DCE=53°,求路灯杆BE的高度.(结果精确到0.1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.732)
29.某学习小组,为了测量旗杆AB的高度,他们在大楼MN第10层D点测得旗杆底端B的俯角是32°,又上到第35层,在C点测得旗杆顶端A的俯角是60°,每层楼高度是2.8米,请你根据以上数据计算旗杆AB的高度.(精确到0.1米,已知:sin32°≈0.37,cos32°≈0.93,tan32°≈0.62,≈1.73)
30.为了监控大桥下坡路段车辆行驶速度,通常会在下引桥处设置电子眼进行区间测速.如图,电子眼位于点P处,离地面的铅锤高度PQ为9米,区间测速的起点为下引桥坡面点A处,此时电子眼的俯角为30°;区间测速的终点为下引桥坡脚点B处,此时电子眼的俯角为60°(A、B、P、Q四点在同一平面).
(1)求路段BQ的长(结果保留根号);
(2)当下引桥坡度i=1:2时,求电子眼区间测速路段AB的长(结果保留根号).
参考答案
一.选择题(共15小题)
1.解:∵∠CAD+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠CAD=∠BCD,
在Rt△BCD中,∵cos∠BCD=,
∴BC==,
故选:B.
2.解:设AB=xm,
在Rt△ABD中,∵∠ADB=45°,
∴AB=BD=xm,
在Rt△ABC中,∵∠ACB=56.3°,且tan∠ACB=,
∴BC==≈x,
由BC+CD=BD得x+10=x,
解得x=30,
∴AB的长约为30m,
故选:B.
3.解:∵PA⊥PB,
∴∠APC=90°,
∵PC=50米,∠PCA=α,
∴tanα=,
∴小河宽PA=PCtan∠PCA=50?tanα(米).
故选:D.
4.解:∵∠BAC=40°,AB=AC,
∴∠ACB=∠ABC=70°,
∵DE⊥BC,
∴∠DEB=90°,
∴∠BDE=90°﹣70°=20°,
∴DE=BD?cos20°=140cos20°,
故选:B.
5.解:如图,过点D作DE⊥OC于点E,
则点D到OB的距离等于OE的长.
∵四边形ABCD是矩形,
∴∠BCD=90°,CD=AB=a,AD=BC=b,
∴∠CDE=∠BCO=x,
∴OC=BC?cosx=bcosx,
CE=CD?sinx=asinx,
∴OE=OC+CE=bcosx+asinx.
则点D到OB的距离等于bcosx+asinx.
故选:C.
6.解:在Rt△ABD中,∠ADB=90°,
则sinA=,cosA=,tanA=,
因此选项A正确,选项B、C、D不正确;
故选:A.
7.解:作AB⊥CB于B,
由题意得,AB=10米,
∵斜坡的坡度i=1:2.4,
∴=,即=,
解得,BC=24,
由勾股定理得,AC===26(米),
故选:D.
8.解:∵某游乐场山顶滑梯的高BC为50米,滑梯的坡比为5:12,
∴=,
则=,
解得:AC=120米,
故AB===130(米).
故选:D.
9.解:∵河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,
∴=,
则AC=4(m),
故AB===4(m).
故选:C.
10.解:∵BC⊥AC,AC=2,∠BAC=α,
∴tanα=,
∴BC=AC?tanα=2tanα,
故选:B.
11.解:过A作AF⊥DE于F,如图所示:
则四边形ABEF为矩形,
∴AB=EF,AF=BE,
∵台阶底端C与顶端D的连线可视作坡度为1:0.75的斜坡,
∴设DE=4x米,则CE=3x米,
由勾股定理得:CD2=DE2+CE2,即402=(4x)2+(3x)2,
解得:x=8,
则CE=3x=24(米),DE=4x=32(米),
∴BE=BC+CE=1+24=25(米),
∴AF=25米,
∵在点D看石雕上边缘点A的俯角为50°,
∴∠DAF=50°,
在Rt△DAF中,tan∠DAF=,
∴DF=AF?tan∠DAF≈25×1.19=29.75(米),
则AB=FE=DE﹣DF=32﹣29.75=2.25(米)
故选:C.
12.解:过点E作EF⊥CD于F,EH⊥AB于H,如图所示:
则∠CEF=36°,四边形DHEF为矩形,
∴DF=EH,
∵坡度比为i=1:2.4,
∴=,
∴AH=2.4EH,
在Rt△AHE中,AE2=AH2+EH2,
即2602=(2.4EH)2+EH2,
解得:EH=100(米),
∴DF=100米,
在Rt△CEF中,sin∠CEF=,
∴sin36°=,
∴CF=110×sin36°≈110×0.6=66(米),
∴CD=CF+DF=66米+100米=166米,
故选:D.
13.解:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.
已知AB=960米,∠BAC=30°,∠EBC=60°,
∵∠BCA=∠EBC﹣∠BAC=30°,
∴∠BAC=∠BCA.
∴BC=BA=960(米).
在Rt△BEC中,sin∠EBC=,
∴CE=BC?sin60°=960×=480(米).
∴CF=CE+EF=(480+300)米,
故选:A.
14.解:在Rt△ABC中,∵sin∠ABC=,即sinα=,
∴AB=,
在Rt△ADC中,∵sin∠ADC=,即sinβ=,
∴AD=,
∴==,
故选:C.
15.解:因为从点A看点B的仰角与从点B看点A的俯角互为内错角,大小相等.
所以小丽在楼上点A处看到楼下点B处小明的俯角是35°,
点B处小明看点A处小丽的仰角是35°.
故选:A.
二.填空题(共8小题)
16.解:在Rt△ABC中,∠ABC=60°,∠ACB=90°,
∴∠BAC=30°,
∵BC=3米,
∴AB=2BC=6(米).
故答案为:6.
17.解:设他沿着垂直方向升高了x米,
∵坡比为1:2.4,
∴他行走的水平宽度为2.4x米,
由勾股定理得,x2+(2.4x)2=1302,
解得,x=50,
即他沿着垂直方向升高了50米,
故答案为:50.
18.解:∵斜坡的坡度i==1:3,铅垂高度=3米
∴水平宽度=3×铅垂高度=3×3=9(米),
故答案为:9.
19.解:如图,过点B作BC垂直于水平面于点C,
∵BC:AC=1:0.75,
∴12:AC=1:0.75,
∴AC=9(米),
∴AB===15(米),
答:该大坝迎水坡AB的长度为15米.
故答案为:15.
20.解:由题意得,∠BAE=60°,DC=AE=10m,AD=EC=1.5m,
在Rt△ABE中,BE=AE?tan∠BAE=10×tan60°=10(m),
∴BC=BE+EC=(10+1.5)(m),
故答案为:(10+1.5).
21.解:连接AD,过点A作AH⊥CD于点H,则四边形ABDH是矩形,
∴AB=DH=m米,
在Rt△ADH中,∠DAH=β,
∴tanβ=,
∴AH=,
在Rt△ACH中,∠CAH=α,
∴CH=AH?tanα=?tanα=(米),
答:两栋教学楼的高度差CH为米.
故答案为:.
22.解:如图,作AE⊥CD于E,则四边形ABCE为矩形,
∴CE=AB=1.5m,AE=BC,
在Rt△ACE中,tan∠CAE=,
∴AE===(m),
在Rt△ADE中,∵∠DAE=45°,
∴△ADE为等腰直角三角形,
∴DE=AE=m,
又∵CE=AB=1.5m,
∴CD=CE+DE=1.5+=(m),
答:建筑物CD的高度为m.
故答案为:.
23.解:由题意可得:AC=DE=6米,
则tan60°===,
解得:BC=6(米),
则BE=(6+1.5)米.
故答案为:(6+1.5).
三.解答题(共7小题)
24.解:过点A作AD⊥BC于点D.如图所示:
在Rt△ACD中,∵∠C=45°,
∴tanC==1,
∴CD=AD,
在Rt△ABD中,∵∠B=64°,
∴tan∠B==2.05,
∴BD=BD,
∵BC=BD+CD=50米,
∴AD+AD=50米,
解得:AD≈33.6(米).
答:河的宽度约为33.6米.
25.解:∵CD⊥AC,
∴∠ACD=90°,
∵∠ABD=135°,
∴∠DBC=45°,
∴∠D=45°,
∴CB=CD,
在Rt△DCB中:CD2+BC2=BD2,
2CD2=8002,
CD=400≈566(米),
答:直线L上距离D点566米的C处开挖.
26.解:过B作BE⊥CD于E,过B作BH⊥AD于H,
则四边形BEDH是矩形,
∴DE=BH,BE=DH,
在Rt△ACE中,∵BC=600,∠CBE=22°,
∴CE=BC?sin22°=600×0.37=222(m),BE=BC?cos22°=600×0.92=552(m),
∴DH=BE=552m,
∵CD=500m,
∴BH=DE=CD﹣CE=500﹣222=278(m),
在Rt△ABH中,∵∠BAH=53°,
∴tan53°=,
∴AH=≈214(m),
∴AD=AH+DH=214+552=766(m),
答:该数学小组行进的水平距离AD为766m.
27.解:在Rt△ABC中,sinA=,
∴AC===≈4.7(m),
答:斜坡AC的长约为4.7m.
28.解:如图,作DF⊥AB于F,设BE的长度为x米,
在Rt△DEC中,∠DCE=53°,
∴∠CDE=90°﹣53°=37°,
∴CE=CD?sin37°≈0.84,DE=CD?cos37°≈1.12,
∵∠DEB=∠B=∠DFB=90°,
∴四边形DEBF是矩形,
∴DE=BF≈1.12,DF=BE=x,
在Rt△ABC中,∠CAB=45°,BC≈x﹣0.84,
∴AB=BC≈x﹣0.84,
∴AF≈x﹣0.84﹣1.12=x﹣1.96,
在Rt△AFD中,∠DAF=60°,AF≈x﹣1.96,DF=x,
∴DF=AF?tan60°,
∴x=(x﹣1.96),
解得:x≈4.6,
答:路灯杆BE的高度约为4.6米.
29.解:过C作CE⊥BA交BA的延长线于点E,过点D作DF⊥BA交BA于点F.
由题意知:
∵点D在第10层,点C在第35层,每层楼高为2.8米,
∴MD=2.8×10=28(米),CM=2.8×35=98(米),
在Rt△DFB中,∠FDB=32°,BF=MD=28,
∴DF==≈≈45.16(米),
在Rt△CEA中,∠ACE=60°,CE=DF≈45.16,
∴EA=CE?tan∠ACE=45.16×tan60°≈45.16×1.73≈78.13(米),
∵BE=CM=98(米)
∴BA=BE﹣AE≈98﹣78.13=19.87≈19.9(米),
答:旗杆AB的高度约为19.9米.
30.解:(1)由题意,∠PBQ=∠TPB=60°,
∵∠PQB=90°,
∴∠BPQ=30°,
∴BQ=PQ?tan30°=9×=3(米).
(2)如图,过点A作AM⊥QB于M,AH⊥PQ于H.
由题意,∠PAH=∠TPA=30°,
设AM=a米,则BM=2a米,
∵∠AHQ=∠HQM=∠AMQ=90°,
∴四边形AHQM是矩形,
∴AH=QM=(3+2a)米,QH=AM=a米,PH=PQ﹣HQ=(9﹣a)米,
在Rt△APH中,tan∠PAH=,
∴=,
解得a=2,
∴AM=2(米),BM=4(米),
∴AB===2(米).
一.选择题(共15小题)
1.如图,电线杆的高度为CD=m,两根拉线AC与BC互相垂直(点A、点D、点B在同一条直线上),若∠CAB=α,则拉线BC的长度可以表示为( )
A.
B.
C.
D.mcosα
2.如图,要测量一条河两岸相对的两点A,B之间的距离,我们可以在岸边取点C和D,使点B,C,D共线且直线BD与AB垂直,测得∠ACB=56.3°,∠ADB=45°,CD=10m,则AB的长约为( )
(sin56.3°≈0.8,cos56.3°≈0.6,tan56.3°≈1.5,sin45°≈0.7,cos45°≈0.7,tan45=1)
A.15m
B.30m
C.35m
D.40m
3.如图,兴趣小组探究活动中,小明要测量小河两岸相对的两点P,A的距离,他和同学利用工具测得PC=50米,∠PCA=α,根据上述测量数据可计算小河宽度PA为( )
A.
米
B.50sinα米
C.
米
D.50tanα米
4.人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点.图2是它的示意图,AB=AC,BD=140cm,∠BAC=40°,则点D离地面的高度DE为( )
A.140sin20°cm
B.140cos20°cm
C.140sin40°cm
D.140cos40°cm
5.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点D到OB的距离等于( )
A.asinx+bsinx
B.acosx+bcosx
C.asinx+bcosx
D.acosx+bsinx
6.比萨斜塔是意大利的著名建筑,其示意图如图所示,设塔顶中心点为点B,塔身中心线AB与垂直中心线AC的夹角为∠A,过点B向垂直中心线AC引垂线,垂足为点D.通过测量可得AB、BD、AD的长度,利用测量所得的数据计算∠A的三角函数值,进而可求∠A的大小.下列关系式正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.sinA=
7.如图,传送带和地面所成斜坡的坡度i=1:2.4,如果它把某物体从地面送到离地面10米高的地方,那么该物体所经过的路程是( )
A.10米
B.24米
C.25米
D.26米
8.如图,某游乐场山顶滑梯的高BC为50米,滑梯的坡比为5:12,则滑梯的长AB为( )
A.100米
B.110米
C.120米
D.130米
9.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,则AB的长度为( )
A.2m
B.4m
C.4m
D.6m
10.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα
B.2tanα
C.2cosα
D.
11.在学校操场旁边的台阶上有一个“翔”的雕塑,雕塑后面是很长的一段台阶CD,意寓拥抱梦想,展翅翱翔.如图,雕塑的上边缘点A距地面平台高度为AB的长,点B距台阶底端C的距离BC=1米,台阶底端C与顶端D的连线可视作坡度为1:0.75的斜坡,且CD=40米.若A,B,C,D四点在同一平面内,且在点D看石雕上边缘点A的俯角为50°,则雕塑“翔”的高度AB约为( )米.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
A.2.21
B.2.20
C.2.25
D.2.31
12.某次暴雨来袭时,需要测量公路AB遇到塌方,运输车辆只能沿从坡度比为i=1:2.4斜坡AE将货物运输到山顶C处,运输车辆到达E处,测得仰角为36°,AE=260米,CE=110米,则山CD的高度为( ).(参考数据:sin36°≈0.6,cos36°≈0.8)
A.137
B.188
C.176
D.166
13.如图,一艘潜水艇在海面下300米的点A处发现其正前方的海底C处有黑匣子,同时测得黑匣子C的俯角为30°,潜水艇继续在同一深度直线航行960米到点B处,测得黑匣子C的俯角为60°,则黑匣子所在的C处距离海面的深度是( )
A.(480+300)米
B.(960+300)米
C.780米
D.1260米
14.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AD与AB的长度之比为( )
A.
B.
C.
D.
15.如果小丽在楼上点A处看到楼下点B处小明的俯角是35°,那么点B处小明看点A处小丽的仰角是( )
A.35°
B.45°
C.55°
D.65°
二.填空题(共8小题)
16.如图,一架梯子斜靠在墙上,梯子与地面的夹角∠B=60°,梯子与墙角的距离BC为3m,则梯子的长AB为
m.
17.如果小明沿着坡度为1:2.4的山坡向上走了130米,那么他的高度上升了
米.
18.已知某斜坡的坡度i=1:3,当铅垂高度为3米时,水平宽度为
米.
19.如图,某堤坝的坝高为12米,如果迎水坡的坡度为1:0.75,那么该大坝迎水坡AB的长度为
米.
20.如图,在一次数学课外实践活动中,小亮在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1.5m,则旗杆高BC为
m(结果保留根号).
21.如图,小明在教学楼AB的楼顶A测得:对面实验大楼CD的顶端C的仰角为α,底部D的俯角为β.如果教学楼AB的高度为m米,那么两栋教学楼的高度差CH为
米.
22.如图,小明想在自己家的窗口A处测量对面建筑物CD的高度,他首先量出窗口A到地面的距离AB为1.5m,又测得从A处看建筑物底部C的俯角为30°,看建筑物顶部D的仰角为45°,且AB,CD都与地面垂直,点A,B,C,D在同一平面内.则建筑物CD的高度
m.
23.高新一中初中校区九年级(一)班课外活动小组为了测得学校旗杆的高度,他们在离旗杆6米的A处,用高为1.5米的仪器测得旗杆顶部B处的仰角为60°,如图所示,则旗杆的高度为
米.(结果保留根号)
三.解答题(共7小题)
24.如图,为了测量河宽,在河的一边沿岸选取B、C两点,对岸岸边有一块石头A,在△ABC中,测得∠B=64°,∠C=45°,BC=50米,求河宽(即点A到边BC的距离)(结果精确到0.1米).
(参考数据:≈1.41,sin64°=0.90,cos64°=0.44,tan64°=2.05)
25.如图,修公路遇到一座山,于是要修一条隧道,为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过点C作直线AB的垂线l,过点B作一直线(在山的旁边经过),与l相交于D点,经测量∠ABD=135°,BD=800m,求直线l上距离D点多远的C处开挖?(≈1.414,精确到1米)
26.5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛峰完成峰顶测量任务,受此消息鼓舞,某数学小组开展了一次测量小山高度的活动,如图,该数学小组从地面A处出发,沿坡角为53°的山坡AB直线上行一段距离到达B处,再沿着坡角为22°的山坡BC直线上行600米到达C处,通过测量数据计算出小山高CD=500m.求该数学小组行进的水平距离AD(结果精确到1m).(参考数据:sin22°≈0.37,cos22°≈0.92,tan22°≈0.32,sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
27.如图,某商场门前的台阶高出地面0.8米,即CB=0.8米,现将此台阶改造成供轮椅行走的斜坡AC,并且设计斜坡的倾斜角∠A为10°.求斜坡AC的长.(结果精确到0.1m)
【参考数据:sin10°=0.17.cos10°=0.98,tan10°=0.18】
28.某中学门口新装了一批太阳能路灯,在路面A点观察点D的仰角为60°,观察点C的仰角为45°,灯管安装处D点与太阳能电池板安装处E点在同一水平线上,已知灯管支架CD长度为1.4米,且∠DCE=53°,求路灯杆BE的高度.(结果精确到0.1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.732)
29.某学习小组,为了测量旗杆AB的高度,他们在大楼MN第10层D点测得旗杆底端B的俯角是32°,又上到第35层,在C点测得旗杆顶端A的俯角是60°,每层楼高度是2.8米,请你根据以上数据计算旗杆AB的高度.(精确到0.1米,已知:sin32°≈0.37,cos32°≈0.93,tan32°≈0.62,≈1.73)
30.为了监控大桥下坡路段车辆行驶速度,通常会在下引桥处设置电子眼进行区间测速.如图,电子眼位于点P处,离地面的铅锤高度PQ为9米,区间测速的起点为下引桥坡面点A处,此时电子眼的俯角为30°;区间测速的终点为下引桥坡脚点B处,此时电子眼的俯角为60°(A、B、P、Q四点在同一平面).
(1)求路段BQ的长(结果保留根号);
(2)当下引桥坡度i=1:2时,求电子眼区间测速路段AB的长(结果保留根号).
参考答案
一.选择题(共15小题)
1.解:∵∠CAD+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠CAD=∠BCD,
在Rt△BCD中,∵cos∠BCD=,
∴BC==,
故选:B.
2.解:设AB=xm,
在Rt△ABD中,∵∠ADB=45°,
∴AB=BD=xm,
在Rt△ABC中,∵∠ACB=56.3°,且tan∠ACB=,
∴BC==≈x,
由BC+CD=BD得x+10=x,
解得x=30,
∴AB的长约为30m,
故选:B.
3.解:∵PA⊥PB,
∴∠APC=90°,
∵PC=50米,∠PCA=α,
∴tanα=,
∴小河宽PA=PCtan∠PCA=50?tanα(米).
故选:D.
4.解:∵∠BAC=40°,AB=AC,
∴∠ACB=∠ABC=70°,
∵DE⊥BC,
∴∠DEB=90°,
∴∠BDE=90°﹣70°=20°,
∴DE=BD?cos20°=140cos20°,
故选:B.
5.解:如图,过点D作DE⊥OC于点E,
则点D到OB的距离等于OE的长.
∵四边形ABCD是矩形,
∴∠BCD=90°,CD=AB=a,AD=BC=b,
∴∠CDE=∠BCO=x,
∴OC=BC?cosx=bcosx,
CE=CD?sinx=asinx,
∴OE=OC+CE=bcosx+asinx.
则点D到OB的距离等于bcosx+asinx.
故选:C.
6.解:在Rt△ABD中,∠ADB=90°,
则sinA=,cosA=,tanA=,
因此选项A正确,选项B、C、D不正确;
故选:A.
7.解:作AB⊥CB于B,
由题意得,AB=10米,
∵斜坡的坡度i=1:2.4,
∴=,即=,
解得,BC=24,
由勾股定理得,AC===26(米),
故选:D.
8.解:∵某游乐场山顶滑梯的高BC为50米,滑梯的坡比为5:12,
∴=,
则=,
解得:AC=120米,
故AB===130(米).
故选:D.
9.解:∵河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,
∴=,
则AC=4(m),
故AB===4(m).
故选:C.
10.解:∵BC⊥AC,AC=2,∠BAC=α,
∴tanα=,
∴BC=AC?tanα=2tanα,
故选:B.
11.解:过A作AF⊥DE于F,如图所示:
则四边形ABEF为矩形,
∴AB=EF,AF=BE,
∵台阶底端C与顶端D的连线可视作坡度为1:0.75的斜坡,
∴设DE=4x米,则CE=3x米,
由勾股定理得:CD2=DE2+CE2,即402=(4x)2+(3x)2,
解得:x=8,
则CE=3x=24(米),DE=4x=32(米),
∴BE=BC+CE=1+24=25(米),
∴AF=25米,
∵在点D看石雕上边缘点A的俯角为50°,
∴∠DAF=50°,
在Rt△DAF中,tan∠DAF=,
∴DF=AF?tan∠DAF≈25×1.19=29.75(米),
则AB=FE=DE﹣DF=32﹣29.75=2.25(米)
故选:C.
12.解:过点E作EF⊥CD于F,EH⊥AB于H,如图所示:
则∠CEF=36°,四边形DHEF为矩形,
∴DF=EH,
∵坡度比为i=1:2.4,
∴=,
∴AH=2.4EH,
在Rt△AHE中,AE2=AH2+EH2,
即2602=(2.4EH)2+EH2,
解得:EH=100(米),
∴DF=100米,
在Rt△CEF中,sin∠CEF=,
∴sin36°=,
∴CF=110×sin36°≈110×0.6=66(米),
∴CD=CF+DF=66米+100米=166米,
故选:D.
13.解:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.
已知AB=960米,∠BAC=30°,∠EBC=60°,
∵∠BCA=∠EBC﹣∠BAC=30°,
∴∠BAC=∠BCA.
∴BC=BA=960(米).
在Rt△BEC中,sin∠EBC=,
∴CE=BC?sin60°=960×=480(米).
∴CF=CE+EF=(480+300)米,
故选:A.
14.解:在Rt△ABC中,∵sin∠ABC=,即sinα=,
∴AB=,
在Rt△ADC中,∵sin∠ADC=,即sinβ=,
∴AD=,
∴==,
故选:C.
15.解:因为从点A看点B的仰角与从点B看点A的俯角互为内错角,大小相等.
所以小丽在楼上点A处看到楼下点B处小明的俯角是35°,
点B处小明看点A处小丽的仰角是35°.
故选:A.
二.填空题(共8小题)
16.解:在Rt△ABC中,∠ABC=60°,∠ACB=90°,
∴∠BAC=30°,
∵BC=3米,
∴AB=2BC=6(米).
故答案为:6.
17.解:设他沿着垂直方向升高了x米,
∵坡比为1:2.4,
∴他行走的水平宽度为2.4x米,
由勾股定理得,x2+(2.4x)2=1302,
解得,x=50,
即他沿着垂直方向升高了50米,
故答案为:50.
18.解:∵斜坡的坡度i==1:3,铅垂高度=3米
∴水平宽度=3×铅垂高度=3×3=9(米),
故答案为:9.
19.解:如图,过点B作BC垂直于水平面于点C,
∵BC:AC=1:0.75,
∴12:AC=1:0.75,
∴AC=9(米),
∴AB===15(米),
答:该大坝迎水坡AB的长度为15米.
故答案为:15.
20.解:由题意得,∠BAE=60°,DC=AE=10m,AD=EC=1.5m,
在Rt△ABE中,BE=AE?tan∠BAE=10×tan60°=10(m),
∴BC=BE+EC=(10+1.5)(m),
故答案为:(10+1.5).
21.解:连接AD,过点A作AH⊥CD于点H,则四边形ABDH是矩形,
∴AB=DH=m米,
在Rt△ADH中,∠DAH=β,
∴tanβ=,
∴AH=,
在Rt△ACH中,∠CAH=α,
∴CH=AH?tanα=?tanα=(米),
答:两栋教学楼的高度差CH为米.
故答案为:.
22.解:如图,作AE⊥CD于E,则四边形ABCE为矩形,
∴CE=AB=1.5m,AE=BC,
在Rt△ACE中,tan∠CAE=,
∴AE===(m),
在Rt△ADE中,∵∠DAE=45°,
∴△ADE为等腰直角三角形,
∴DE=AE=m,
又∵CE=AB=1.5m,
∴CD=CE+DE=1.5+=(m),
答:建筑物CD的高度为m.
故答案为:.
23.解:由题意可得:AC=DE=6米,
则tan60°===,
解得:BC=6(米),
则BE=(6+1.5)米.
故答案为:(6+1.5).
三.解答题(共7小题)
24.解:过点A作AD⊥BC于点D.如图所示:
在Rt△ACD中,∵∠C=45°,
∴tanC==1,
∴CD=AD,
在Rt△ABD中,∵∠B=64°,
∴tan∠B==2.05,
∴BD=BD,
∵BC=BD+CD=50米,
∴AD+AD=50米,
解得:AD≈33.6(米).
答:河的宽度约为33.6米.
25.解:∵CD⊥AC,
∴∠ACD=90°,
∵∠ABD=135°,
∴∠DBC=45°,
∴∠D=45°,
∴CB=CD,
在Rt△DCB中:CD2+BC2=BD2,
2CD2=8002,
CD=400≈566(米),
答:直线L上距离D点566米的C处开挖.
26.解:过B作BE⊥CD于E,过B作BH⊥AD于H,
则四边形BEDH是矩形,
∴DE=BH,BE=DH,
在Rt△ACE中,∵BC=600,∠CBE=22°,
∴CE=BC?sin22°=600×0.37=222(m),BE=BC?cos22°=600×0.92=552(m),
∴DH=BE=552m,
∵CD=500m,
∴BH=DE=CD﹣CE=500﹣222=278(m),
在Rt△ABH中,∵∠BAH=53°,
∴tan53°=,
∴AH=≈214(m),
∴AD=AH+DH=214+552=766(m),
答:该数学小组行进的水平距离AD为766m.
27.解:在Rt△ABC中,sinA=,
∴AC===≈4.7(m),
答:斜坡AC的长约为4.7m.
28.解:如图,作DF⊥AB于F,设BE的长度为x米,
在Rt△DEC中,∠DCE=53°,
∴∠CDE=90°﹣53°=37°,
∴CE=CD?sin37°≈0.84,DE=CD?cos37°≈1.12,
∵∠DEB=∠B=∠DFB=90°,
∴四边形DEBF是矩形,
∴DE=BF≈1.12,DF=BE=x,
在Rt△ABC中,∠CAB=45°,BC≈x﹣0.84,
∴AB=BC≈x﹣0.84,
∴AF≈x﹣0.84﹣1.12=x﹣1.96,
在Rt△AFD中,∠DAF=60°,AF≈x﹣1.96,DF=x,
∴DF=AF?tan60°,
∴x=(x﹣1.96),
解得:x≈4.6,
答:路灯杆BE的高度约为4.6米.
29.解:过C作CE⊥BA交BA的延长线于点E,过点D作DF⊥BA交BA于点F.
由题意知:
∵点D在第10层,点C在第35层,每层楼高为2.8米,
∴MD=2.8×10=28(米),CM=2.8×35=98(米),
在Rt△DFB中,∠FDB=32°,BF=MD=28,
∴DF==≈≈45.16(米),
在Rt△CEA中,∠ACE=60°,CE=DF≈45.16,
∴EA=CE?tan∠ACE=45.16×tan60°≈45.16×1.73≈78.13(米),
∵BE=CM=98(米)
∴BA=BE﹣AE≈98﹣78.13=19.87≈19.9(米),
答:旗杆AB的高度约为19.9米.
30.解:(1)由题意,∠PBQ=∠TPB=60°,
∵∠PQB=90°,
∴∠BPQ=30°,
∴BQ=PQ?tan30°=9×=3(米).
(2)如图,过点A作AM⊥QB于M,AH⊥PQ于H.
由题意,∠PAH=∠TPA=30°,
设AM=a米,则BM=2a米,
∵∠AHQ=∠HQM=∠AMQ=90°,
∴四边形AHQM是矩形,
∴AH=QM=(3+2a)米,QH=AM=a米,PH=PQ﹣HQ=(9﹣a)米,
在Rt△APH中,tan∠PAH=,
∴=,
解得a=2,
∴AM=2(米),BM=4(米),
∴AB===2(米).
