2021—2022学年鲁教版九年级数学上册第1章反比例函数综合 优生辅导专题提升训练(word版含答案)
文档属性
| 名称 | 2021—2022学年鲁教版九年级数学上册第1章反比例函数综合 优生辅导专题提升训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 810.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 20:09:46 | ||
图片预览



文档简介
2021年鲁教版九年级数学上册《第1章反比例函数综合》优生辅导专题提升训练(附答案)
1.已知反比例函数y=的图象经过点A(2,3).
(1)求该反比例函数的表达式;
(2)如图,在反比例函数y=的图象上点A的右侧取点C,过点C作x轴的垂线交x轴于点H,过点A作y轴的垂线交直线CH于点D.
①过点A,点C分别作x轴,y轴的垂线,两线相交于点B,求证:O,B,D三点共线;
②若AC=2OA,求证:∠AOD=2∠DOH.
2.定义:有一组对边平行,有一个内角是它对角的一半的凸四边形叫做半对角四边形,如图1,直线l1∥l2,点A,D在直线l1上,点B,C在直l2上,若∠BAD=2∠BCD,则四边形ABCD是半对角四边形.
(1)如图2,点E是矩形ABCD的边AD上一点,AB=1,AE=2.若四边形ABCE为半对角四边形,求AD的长:
(2)如图3,以?ABCD的顶点C为坐标原点,边CD所在直线为x轴,对角线AC所在直线为y轴,建立平面直角坐标系.点E是边AD上一点,满足BC=AE+CE.求证:四边形ABCE是半对角四边形;
(3)在(2)的条件下,当AB=AE=2,∠B=60°时,将四边形ABCE向左平移a(a>0)个单位后,恰有两个顶点落在反比例函数y=的图象上,求k的值.
3.如图,正比例函数y=x和反比例函数y=(x>0)的图象都经过点B(a,6),过点B且平行于x轴的直线交y轴于A,点C在AB的延长线上,CD∥y轴交反比例函数图象于D,连接CO,DO.
(1)求反比例函数的表达式;
(2)若∠ABO=∠OCD,求四边形OBCD的面积.
4.在平面直角坐标系xOy中,函数y=(x>0)的图象与直线y=x+1交于点A(2,m).
(1)求k、m的值;
(2)横、纵坐标都是整数的点叫做整点.已知点P(n,0),过点P作平行于y轴的直线,交直线y=x+1于点B,交函数y=(x>0)的图象于点C.将函数y=(x>0)的图象在点A、C之间的部分与线段AB、DC所围成的区域内部(不包括边界)记作图形G.
①当n=4时,直接写出图形G内的整点坐标;
②若图形G内恰有2个整点,直接写出n的取值范围.
5.如图:在平面直角坐标系中,菱形ABCD的顶点D在y轴上,A,C两点的坐标分别为(2,0),(2,m),直线CD:y1=ax+b与双曲线:y2=交于C,P(﹣4,﹣1)两点.
(1)求双曲线y2的函数关系式及m的值;
(2)判断点B是否在双曲线上,并说明理由;
(3)当y1>y2时,请直接写出x的取值范围.
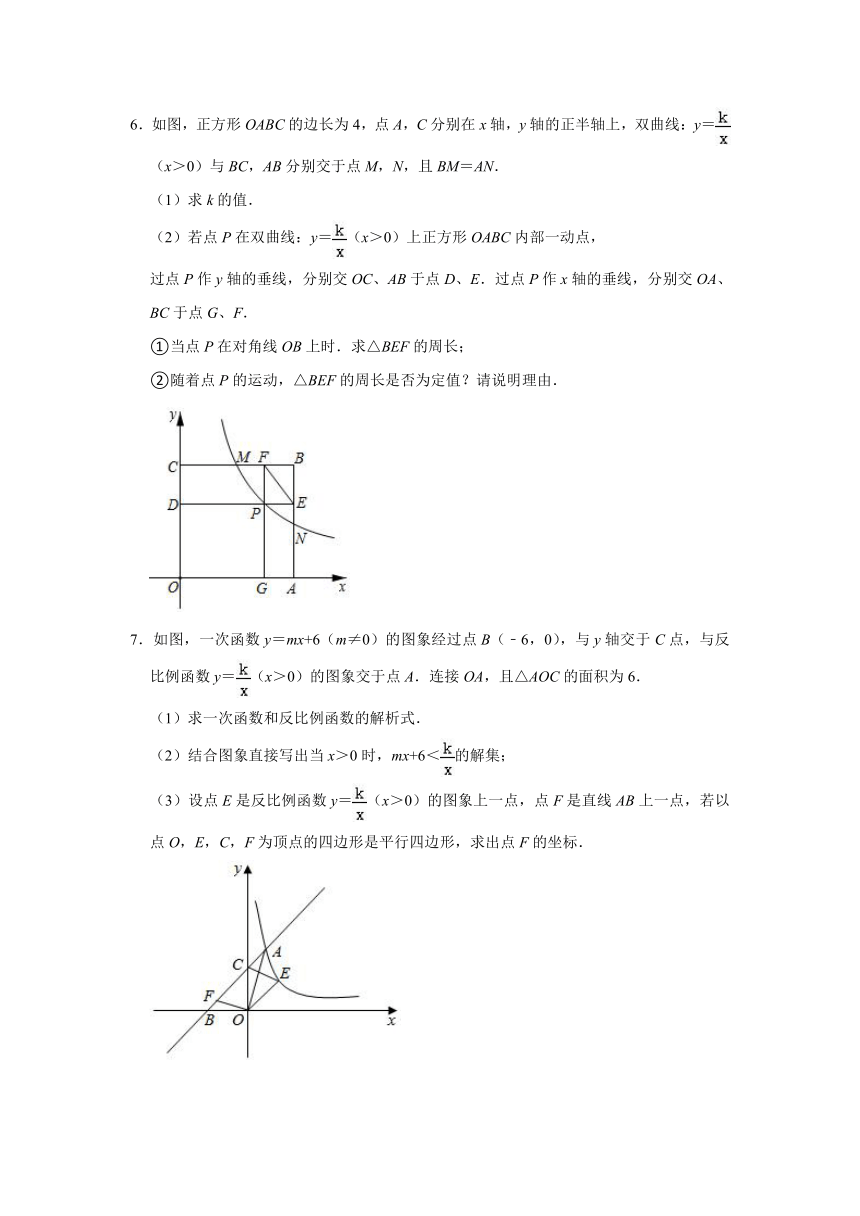
6.如图,正方形OABC的边长为4,点A,C分别在x轴,y轴的正半轴上,双曲线:y=(x>0)与BC,AB分别交于点M,N,且BM=AN.
(1)求k的值.
(2)若点P在双曲线:y=(x>0)上正方形OABC内部一动点,
过点P作y轴的垂线,分别交OC、AB于点D、E.过点P作x轴的垂线,分别交OA、BC于点G、F.
①当点P在对角线OB上时.求△BEF的周长;
②随着点P的运动,△BEF的周长是否为定值?请说明理由.
7.如图,一次函数y=mx+6(m≠0)的图象经过点B(﹣6,0),与y轴交于C点,与反比例函数y=(x>0)的图象交于点A.连接OA,且△AOC的面积为6.
(1)求一次函数和反比例函数的解析式.
(2)结合图象直接写出当x>0时,mx+6<的解集;
(3)设点E是反比例函数y=(x>0)的图象上一点,点F是直线AB上一点,若以点O,E,C,F为顶点的四边形是平行四边形,求出点F的坐标.
8.如图在平面直角坐标系中,等腰Rt△AOB的斜边OB在x轴正半轴上,直线y=3x﹣4经过等腰Rt△AOB的直角顶点A,交y轴于C点,双曲线y=也经过A点.
(1)求点A的坐标和k的值;
(2)过点B作BQ⊥x轴交双曲线于点Q,连接AQ,过点A作AP⊥AQ交x轴于点P,连接PQ,求证:△APQ是等腰直角三角形,并求出此时点Q的坐标.(请根据题意自行画图)
9.如图,在平面直角坐标系中,点B的坐标为(6,4),反比例函数y=(x>0)的图象交矩形OABC的边BC,AB于D、E两点,连接DE,AC.
(1)当点D是BC的中点时,k=
,点E的坐标为
;
(2)设点D的横坐标为m.
①请用含m的代数式表示点E的坐标,
②求证:DE∥AC.
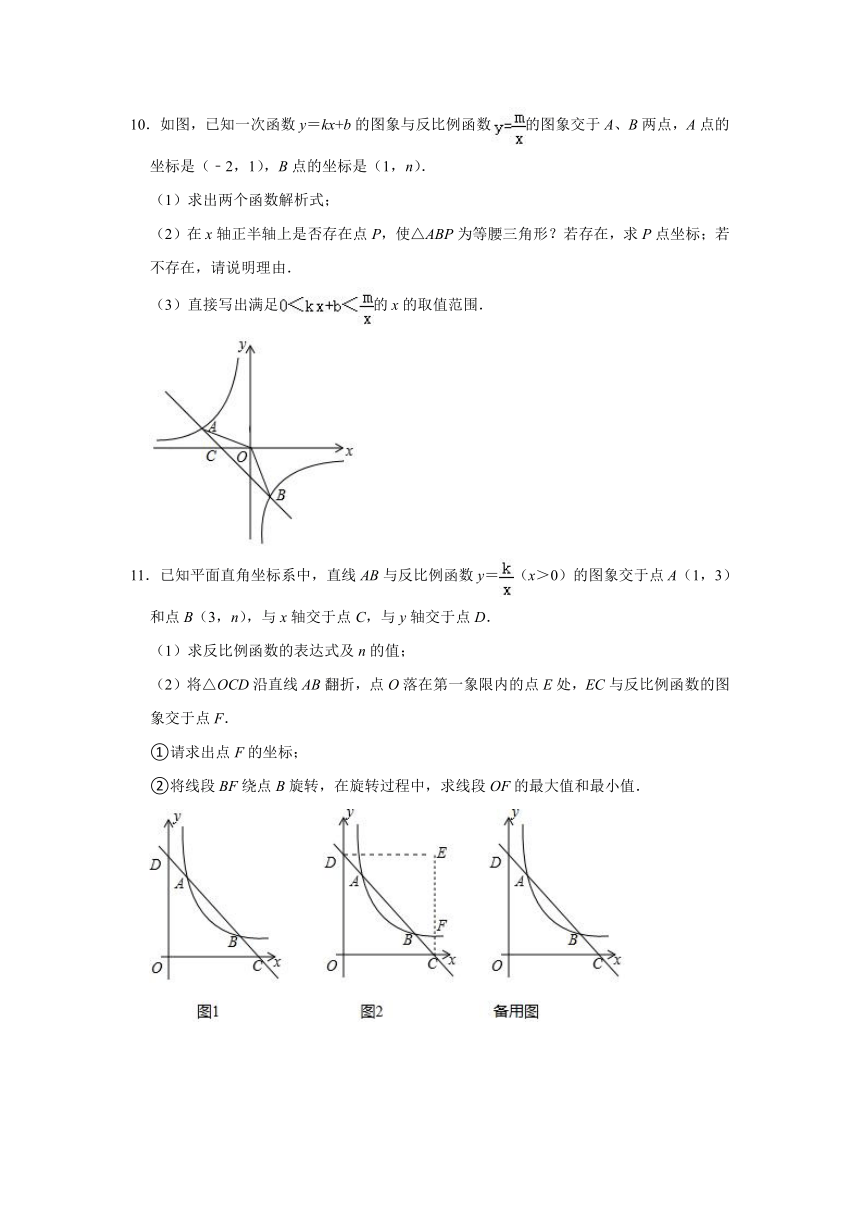
10.如图,已知一次函数y=kx+b的图象与反比例函数的图象交于A、B两点,A点的坐标是(﹣2,1),B点的坐标是(1,n).
(1)求出两个函数解析式;
(2)在x轴正半轴上是否存在点P,使△ABP为等腰三角形?若存在,求P点坐标;若不存在,请说明理由.
(3)直接写出满足的x的取值范围.
11.已知平面直角坐标系中,直线AB与反比例函数y=(x>0)的图象交于点A(1,3)和点B(3,n),与x轴交于点C,与y轴交于点D.
(1)求反比例函数的表达式及n的值;
(2)将△OCD沿直线AB翻折,点O落在第一象限内的点E处,EC与反比例函数的图象交于点F.
①请求出点F的坐标;
②将线段BF绕点B旋转,在旋转过程中,求线段OF的最大值和最小值.
12.如图,直线AC与函数y=﹣的图象相交于点A(﹣1,m),与x轴交于点C(5,0).
(1)求m的值及直线AC的解析式;
(2)直线AE在直线AC的上方,满足∠CAE=∠CAO,求直线AE的解析式;
(3)若D是线段AC上一点将OD绕点O逆时针旋转90°得到OD',点D'恰好落在函数y=﹣的图象上,求点D的坐标.
13.如图,直线y=x,与反比例函数y=在第一象限内的图象相交于点A(m,3).
(1)求该反比例函数的表达式;
(2)将直线y=x沿y轴向上平移,与反比例函数在第一象限内的图象相交于点B,与y轴交于点C,若,连接AB、OB.请判断AB与OA的位置关系,并说明理由;
(3)在(2)的条件下,在射线OA上是否存在一点P,使△PAB与△BAO相似,若存在,请直接写出P点坐标;不存在,请说明理由.
14.如图,在平面直角坐标系中已知四边形ABCD为菱形,且A(0,3),B(﹣4,0).
(1)求过点C的反比例函数表达式;
(2)设直线l与(1)中所求函数图象相切,且与x轴,y轴的交点分别为M,N,O为坐标原点.求证:△OMN的面积为定值.
15.模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
建立函数模型
设矩形相邻两边的长分别为x,y,由矩形的面积为4,得xy=4,即y=;由周长为m,得2(x+y)=m,即y=﹣x+满足要求的(x,y)应是两个函数图象在第一象限内交点的坐标.
作函数图象
(1)①当反比例y=(x>0)的图象与直线y=﹣x+有唯一交点(2,2)时,周长m的值为
;
②交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
解决问题
(2)若能生产出面积为4的矩形模具,则周长m的取值范围为
.
16.如图,一次函数y=﹣x+4与反比例函数y=(x>0)的图象在第一象限交于M,N两点,P是MN上一个动点(点P不与点M,N重合),过点P作PA⊥y轴,PB⊥x轴,垂足为A,B,交反比例函数于点D,点C.
(1)当AP=3AO时,求点D的坐标;
(2)连接AB,CD,若D是AP的中点,试判断AB与CD的位置关系,并说明理由;
(3)点P在运动过程中,AB是否具有最小值,若有,求出最小值;若没有,请说明理由.
17.已知:如图,双曲线y=(k≠0)与直线y=mx(m≠0)交于A(,3)、B两点,将直线AB向下平移n个单位,平移后的直线与双曲线在第一象限的分支交于点C,点D是x轴上一动点.
(1)求双曲线和直线的函数表达式;
(2)连接AD,当点C是线段AD中点时,求n的值;
(3)若点E是双曲线上任意一点,当△ADE是以AE为斜边的直角三角形,且∠DAE=30°时,求点E的坐标.
18.如图,在平面直角坐标系中,矩形ABCO的顶点A、C分别在x轴和y轴的正半轴上,顶点B的坐标为(4,2),双曲线y=(x>0)交BC于点D,交AB于点F,其中BD=.
(1)求反比例函数y=的表达式及F点坐标;
(2)判断DF与AC的位置关系,并说明理由;
(3)点N在y轴正半轴上,反比例函数图象上是否存在一点M,使△DMN是以DM为直角边的等腰直角三角形,若存在,直接写出点M的坐标;若不存在,请说明理由.
19.在平面直角坐标系中,正方形ABCD的位置如图(1)所示,且点A,C在反比例函数y=的图象上,已知点A的横坐标为﹣2,点C的纵坐标为﹣1.
(1)求k的值.
(2)如图(2),AD交y轴于点E,过点B的直线y=x+b交CD于点F,连接EF.求证:△DEF的周长为定值.
20.如图,在平面直角坐标系中,矩形ABCD的顶点B、C在x轴上,A、D在第一象限,反比例函数y=(x>0)的图象经过点A,交CD于点E,OB=2,AB=3.
(1)求k的值;
(2)若点E恰好是DC的中点.
①求直线AE的函数解析式;
②根据图象回答,在第一象限内,当x取何值时,反比例函数的函数值大于直线AE对应函数的函数值?
③若直线AE与x轴交于点M,与y轴交于点N,请你判断线段AN与线段ME的大小关系,并说明理由.
21.如图1,矩形OABC的顶点A、C分别落在x轴、y轴的正半轴上,点B(4,3),反比例函数y=(x>0)的图象与AB、BC分别交于D、E两点,BD=1,点P是线段OA上一动点.
(1)求反比例函数关系式和点E的坐标;
(2)如图2,连接DE、PE、PD,求△PDE周长的最小值;
(3)如图3,当∠PDO=45°时,求线段OP的长.
参考答案
1.(1)解:∵反比例函数y=的图象经过点A(2,3),
∴3=,
∴m=6,
∴反比例函数的解析式为y=.
(2)证明:①过点A作AM⊥x轴于M,过点C作CN⊥y轴于N,AM交CN于点B,连接OB.
∵A(2,3),点C在y=的图象上,
∴可以设C(m,),则B(2,),D(m,3),
∴∠BOM=∠DOH,
∴O,B,D共线.
②设AC交BD于J.
∵AD⊥y轴,CB⊥y轴,
∴AD∥CB,
∵AM⊥x轴,DH⊥x轴,
∴AB∥CD,
∴四边形ABCD是平行四边形,
∵∠ADC=90°,
∴四边形ABCD是矩形,
∴AJ=JC=JD=JB,
∵AC=2OA,
∴AO=AJ,
∴∠AOJ=∠AJO,
∵∠AJO=∠JAD+∠JDA,
∵AD∥OB,
∴∠DOH=∠ADJ,
∵JA=JD,
∴∠JAD=∠ADJ,
∴∠AOD=2∠ADJ=∠DOH.
2.解:(1)∵四边形ABCE为半对角四边形,
∴∠BCE=45°,
∴∠DEC=∠DCE=45°,
∴CD=DE=1,
∴AD=AE+DE=3.
(2)证明∵四边形ABCD为平行四边形,
∴BC∥AD,BC=AD=AE+ED=AE+CE,
∴CE=ED,
∴∠AEC=2∠EDC=2∠B,
又∵AE∥BC,
∴四边形ABCE是半对角四边形;
(3)由题意,可知:点A的坐标为(0,6),点B的坐标为(2,6),点E的坐标为(﹣,3).
(i)当点A,E向左平移a(a>0)个单位后落在反比例函数的图象上时,﹣a?6=(﹣﹣a)?3,
解得:a=,
∴k=﹣6a=﹣6;
(ii)当点B,E向左平移a(a>0)个单位后落在反比例函数的图象上时,(2﹣a)?6=(﹣﹣a)?3,
解得:a=5,
∴k=3(﹣﹣a)=﹣18.
综上所述:k的值为为﹣6或﹣18.
3.解:(1)∵正比例函数y=x和反比例函数y=(x>0)的图象都经过点B(a,6),
∴令y=6,则,
∴x=4,
∴B(4,6),
∴k=24,
∴反比例函数的表达式为;
(2)∵CD∥y轴,
∴∠OCD=∠AOC,
又∠ABO=∠OCD,
∴∠AOC=∠ABO,
∵∠OAC=∠BAO=90°,
∴△OAC∽△BAO,
∴,
∴AO2=AB?AC,
∵B的坐标为(4,6),且AB∥x轴,
∴AO=6,AB=4,
∴36=4AC,
∴AC=9,
∴C(9,6),
∵CD∥y轴,
∴D(9,),
∴,
S四边形OBCD=S△BOC+S△COD==30.
4.解:(1)∵点A(2,m)在直线y=x+1上,
∴m=×2+1=2.
∴A(2,2).
∵点A(2,2)在函数y=(x>0)的图象上,
∴k=4.
(2)①当n=4时,点B(4,3),C(4,1).
∵整点在图形G的内部,
∴2<x<4,且x为整数,
∴x=3.
当x=3时,y=x+1=×3+1=,
y==.
∴.
∵y为整数,
∴y=2.
∴图形G内的整点坐标为(3,2).
②由①知当x=3时,,此时整点为(3,2)共1个;
当x=4时,1<y<3,此时整点为(4,2),1个;
当x=5时,,此时整点有(5,1),(5,2),(5,3),3个;
∵图形G恰好有2个整点,
∴4<n<5.
当x=1时,1.5<y<4,此时整点为(1,2),(1,3),2个,
∴0<n<1.
综上所述,n的取值范围为:4<n<5或0<n<1.
5.解:(1)
连接AC,BD相交于点E,
∵四边形ABCD是菱形,
∴DE=BE,AE=CE,AC⊥BD,
∵A(2,0),C(2,m),
∴E(2,m),AC∥y轴,
∴BD⊥y轴,
∴点D(0,m),B(4,m),
∵点C(2,m),D(0,m),P(﹣4,﹣1)在直线CD上,
∴,
∴,
∴点C(2,2),
∵点C在双曲线y2=上,
∴k=2×2=4,
∴双曲线的函数关系式为y2=;
(2)由(1)知,m=2,B(4,m),
∴B(4,1),
由(1)知双曲线的解析式为y2=;
∵4×1=4,
∴点B在双曲线上;
(3)由(1)知C(2,2),
由图象知,当y1>y2时的x值的范围为﹣4<x<0或x>2.
6.解:(1)∵正方形OABC的边长为4,
∴OA=OC=BC=4,
设点M(m,4),
∴CM=m,
∴BM=BC﹣CM=4﹣m,
∵AN=BM,
∴AN=4﹣m,
∴N(4,4﹣m),
∵点M,N都在双曲线:y=(x>0)上,
∴k=4m=4(4﹣m),
∴m=2,k=8;
(2)由(1)知,k=8,
∴双曲线的解析式为y=,M(2,4),N(4,2),
∵点P在双曲线:y=(x>0)上正方形OABC内部一动点,
∴设P(n,),
①∵正方形OABC的边长为4,
∴B(4,4),
∴直线OB的解析式为y=x,
∵点P在对角线OB上,
∴n=,
∴n=2或n=﹣2(舍),
∴P(2,2),
∵PD⊥y轴,PG⊥x轴,
∴E(2,4),F(4,2),
∴BF=4﹣2,BE=4﹣2,EF=BE=4﹣4,
∴△BEF的周长为4﹣2+4﹣2+4﹣4=4;
②随着点P的运动,△BEF的周长是定值,为4,
理由:∵PD⊥y轴,PG⊥x轴,
∴F(n,4),E(4,),
∴BF=4﹣n,BE=4﹣,
根据勾股定理得,EF====n+﹣4,
∴△BEF的周长为4﹣n+4﹣+n+﹣4=4,
即随着点P的运动,△BEF的周长是定值,其值为4.
7.解:(1)∵一次函数y=mx+6(m≠0)的图象经过点B(﹣6,0),
∴﹣6m+6=0,得m=1,
∴一次函数解析式为y=x+6;
当x=0时,y=6,
∴CO=6,
∵△AOC的面积为6.
∴,
∴xA=2,
当x=2时,y=x+6=8,
∴点A坐标(2,8),
∵反比例函数y=(x>0)的图象经过点A,
∴k=16,
∴反比例函数的解析式为:y=;
(2)结合图象可知当x>0时,mx+6<的解集是0<x<2;
(3)①当CO为边时,如图1,EF∥CO且EF=CO,
设点E坐标为(m,),则点F的坐标为(m,m+6),
∴EF=|﹣m﹣6|,
∴|﹣m﹣6|=6,
当﹣m﹣6=6时,
解得m=4或﹣4(﹣4舍去)此时点F坐标为(4,10);
当﹣m﹣6=﹣6时,
解得m=2﹣6或﹣2﹣6(负值舍去),此时点F坐标为(2﹣6,2);
②当CO为对角线时,如图2,则CO与FE互相平分,
设点E坐标为(m,),点F的坐标为(n,n+6),
由中点坐标公式得,
解得m=4,n=﹣4,此时点F坐标为(﹣4,2),
综上.点N坐标为(4,10)或(2﹣6,2)或(﹣4,2).
8.解:(1)过点A分别作AM⊥y轴于M点,AN⊥x轴于N点,
∵△AOB是等腰直角三角形,
∴AM=AN.
设点A的坐标为(a,a),
∵点A在直线y=3x﹣4上,
∴a=3a﹣4,
解得a=2,
则点A的坐标为(2,2),
∵双曲线y=也经过A点,
∴k=2×2=4;
(2)在△AOP与△ABQ中,
∵∠OAB﹣∠PAB=∠PAQ﹣∠PAB,
∴∠OAP=∠BAQ,
在△AOP和△ABQ中,
,
∴△AOP≌△ABQ(ASA),
∴AP=AQ,
∴△APQ是所求的等腰直角三角形.
∵点A的坐标为(2,2),△OAB为等腰直角三角形,
则OB=4,故B(4,0),
故点Q的横坐标为4,
由(1)知,反比例函数表达式为y=,
当x=4时,y==1,
故Q(4,1).
9.解:(1)∵点D是BC的中点,则点D(3,4),
将点D(3,4)代入反比例函数表达式得:4=,解得k=12;
故反比例函数的表达式为y=,
当x=6时,y===2,
故点E的坐标为(6,2),
故答案为:12,(6,2);
(2)①由题意得,点D的坐标为(m,4),
则k=4m,
则反比例函数表达式为y=,
当x=6时,y==,
即点E的坐标为(6,);
②由①知,BD=6﹣m,BE=4﹣,
∴=1﹣m,=1﹣m=,
∴DE∥AC.
10.解:(1)∵反比例函数y=的图象过点A(﹣2,1),
∴m=﹣2×1=﹣2,
∴反比例函数的解析式为y=﹣,
∵反比例函数y=﹣的图象过点B(1,n),
∴﹣2=1×n,
∴n=﹣2,
∴B(1,﹣2),
∵一次函数y=kx+b的图象过A,B两点,
∴,
解得k=﹣1,b=﹣1,
∴一次函数的解析式为y=﹣x﹣1;
(2)设点P(m,0)(m>0),
∵A(﹣2,1),B(1,﹣2),
∴AB2=(﹣2﹣1)2+[1﹣(﹣2)]2=18,AP2=(m+2)2+1=m2+4m+5,BP2=(m﹣1)2+4=m2﹣2m+5,
∵△ABP为等腰三角形,
∴①当AP=AB时,AP2=AB2,
∴m2+4m+5=18,
∴m=﹣2﹣(舍)或m=﹣2+,
∴P(﹣2+,0),
②当AP=BP时,AP2=BP2,
∴m2+4m+5=m2﹣2m+5,
∴m=0(舍),
③当AB=BP时,AB2=BP2,
∴m2﹣2m+5=18,
∴m=1﹣(舍)或m=1+,
∴P(1+,0),
即满足条件的点P的坐标为(﹣2+,0)或(1+,0).
(3)∵一次函数的解析式为y=﹣x﹣1,其图象与x轴交于点C,
∴点C的坐标为(﹣1,0),
∵CA(﹣2,1),
∴0<kx+b<的x的取值范围是﹣2<x<﹣1.
11.解:(1)将A(1,3)代入y=(x>0)中得,
3=,
解得:k=3,
∴反比例函数解析式为:y=,
∵B(3,n)在反比例函数y=上,
∴n==1;
(2)①设直线DC的解析式为:y=kx+b(k≠0),图象经过点A(1,3)、B(3,1),将其代入得:
,
解得:,
∴直线DC的解析式为:y=﹣x+4,
令y=0,则0=﹣x+4,解得x=4,
令x=0,则y=4,
∴OD=OC=4,
又∵将△OCD沿直线AB翻折,点落在第一象限内的点E处,
∴DE=4,
即F点的横坐标为4,且在反比例函数的图象上,
∴当x=4时,y=,
故F点坐标为(4,);
②由①可知,B(3,1),F(4,),
∴BF==,OB==,
由题意可知;线段BF绕点B旋转过程中,F始终在以B点为圆心,BF为半径的圆上,
情况一:当BF旋转到线段OB上时,如图所示,OF1为线段OF的最小值,
∴OFmin=OB﹣BF1=,
情况二:当BF旋转到线段OB的延长线上时,如图所示,OF2为线段OF的最大值,
∴OFmax=OB+BF2=,
综上,线段BF绕点B在旋转过程中,线段OF的最大值为,最小值为.
12.解:(1)将点A(﹣1,m)代入函数y=﹣中得:
m==6,
设直线AC的解析式为y=kx+b(k≠0),经过A(﹣1,6),C(5,0)两点,将其代入得:
,
解得:,
∴直线AC的解析式为:y=﹣x+5;
(2)在AE上截取AF,使得AF=AO,则:
在△ACO和△ACF中,
,
∴△ACO≌△ACF(SAS),
∴AF=AO==,
在y=﹣x+5中,令y=0,则x=5,
∴OC=CF=5
设F(a,b),
∴AF=,FC=,
∴,
解得:或(舍去),
∴点F坐标为(5,5),
设直线AE的解析式为:y=k'x+b'(k'≠0),经过点F(5,5),点A(﹣1,6),将其代入得:
,
解得:,
∴直线AE的解析式:y=﹣,
(3)设OD绕点O逆时针旋转90°得到OD',则∠DOD'=90°,过点D作DN⊥x轴交于点N,过点D'作D'M⊥x轴交于点M,
∵∠D'OM+∠DON=90°,∠D'OM+∠OD'M=90°,
在△D'OM和△ODN中,
,
∴△D'OM≌△ODN(AAS),
∴DN=OM,NO=D'M,
设D(d,﹣d+5),则:DN=OM=﹣d+5,NO=D'M=d,
∵点D'在第二象限,
∴D’(d﹣5,d)且在y=上,
∴d=﹣,
解得:d1=2,d2=3,
经检验符合题意,
∴D坐标为(2,3)或(3,2).
13.解:(1)∵点A(m,3)在直线y=x,
∴3=m,
∴m=3,
∴点A(3,3),
∵点A(3,3)在反比例函数y=上,
∴k=3×3=9,
∴y=;
(2)OA⊥AB,理由如下:
如图,作BE⊥y轴于E,AF⊥y轴于F.
∴∠BEO=∠AFO=90°,
∵BC∥AO,
∴∠ECB=∠FOA,
∴△BCE∽△AOF,
∴=,
∴=,
∴BE=,
∴B(,9),
又∵A(3,3),
∴OA2=36,OB2=84,AB2=48,
∴OA2+AB2=OB2,
∴∠OAB=90°,
∴OA⊥AB.
(3)如图,①当△APB∽△ABO时,=,
由(2)知,AB=4,OA=6,即
=,
∴AP=8,
∵OA=6,
∴OP=14,
过点A作AH⊥x轴于H,
∵A(3,3),
∴OH=3,AH=3,
在Rt△AOH中,
∴∠AOH=30°.
过点P作PG⊥x轴于G,
在Rt△APG中,∠POG=30°,OP=14,
∴PG=7,OG=7
,
∴P(7,7).
②当△PAB∽△OAB时,==1.
∴AP=OA,即A是OP的中点,
由(2)知,A(3,3),
∴P(6,6).
综上所述,符合条件的点P的坐标是(7,7)或(6,6).
14.(1)解:∵点A的坐标为(0,3),点B的坐标为(﹣4,0),
∴OA=3,OB=4.
在Rt△AOB中,OA=3,OB=4,
∴AB==5.
∵四边形ABCD为菱形,
∴BC∥y轴,且BC=AB=5,
∴点C的坐标为(﹣4,﹣5).
∵点C在反比例函数y=的图象上,
∴k=(﹣4)×(﹣5)=20,
∴过点C的反比例函数表达式为y=.
(2)证明:设直线l的解析式为y=mx+n(m≠0),
将y=mx+n代入y=得:mx+n=,
整理得:mx2+nx﹣20=0.
∵直线l与反比例函数y=的图象相切,
∴△=n2﹣4×m×(﹣20)=0,
∴n2=﹣80m.
当x=0时,y=m×0+n=n,
∴点N的坐标为(0,n);
当y=0时,mx+n=0,解得:x=﹣,
∴点M的坐标为(﹣,0).
∴S△OMN=|n|×|﹣|=||=40,
∴△OMN的面积为定值.
15.解:图象如下所示:
(1)①把点(2,2)代入y=﹣x+得:
2=﹣2+,
解得:m=8,
故答案是:8;
②由①知:0个交点时,0<m<8;2个交点时,m>8;1个交点时,m=8;
(2)联立y=和y=﹣x+并整理得:x2﹣mx+4=0,
△=m2﹣4×4≥0时,两个函数有交点,
解得:m≥8.
故答案是:m≥8.
16.解:设点P的坐标为(m,﹣m+4),则点A、B的坐标分别为(0,﹣m+4)、(m,0).
(1)当AP=3AO时,即m=3(﹣m+4),
解得m=3,
故点A的坐标为(0,1),
当y=1时,即1=,
解得x=1,
故点D的坐标为(1,1);
(2)∵D是AP的中点,故点D的坐标为(m,﹣m+4),
将点D的坐标代入反比例函数表达式并整理得:4﹣m=,
设直线AB的表达式为y=kx+b,则,解得,
即直线AB表达式中的k值为﹣;
同理可得,直线CD表达式中的k值为﹣,
故直线AB∥CD;
(3)有,理由:
由题意得,四边形OAPB为矩形,
则AB=OP===≥2,
故AB有最小值为2.
17.解:(1)将点A的坐标代入反比例函数表达式得:3=,解得k=3,
设直线AB的表达式为y=mx,将点A的坐标代入上式得:3=m,解得m=,
故反比例函数和直线AB的表达式分别为y=和y=x;
(2)平移后直线的表达式为y=x﹣n,
连接A、C、D,分别过点A、C作x轴的垂线,垂足分别为M、N,
∵AM∥CN,点C是线段AD中点,
故CN是△AMD的中位线,设点C的坐标为(a,),
则CN=AM,即=×3,解得a=2,
故点C的坐标为(2,),
将点C的坐标代入y=x﹣n得:=?2﹣n,
解得n=;
(3)过点A、E分别作x轴的垂线,垂足分别为H、N,
在Rt△ADE中,∠DAE=30°,则AD:DE=,
∵∠ADH+∠EDN=90°,∠EDN+∠DEN=90°,
∴∠ADH=∠DEN,
∴Rt△AHD∽Rt△DNE,
∴,
设点D的坐标为(t,0),点E的坐标为(b,),
则AH=3,DH=t﹣,DN=b﹣t,EN=,
即,
解得b=3或﹣,
故点E的坐标为(﹣,﹣3)或(3,1).
18.解:(1)∵四边形ABCD是矩形,
∴BC∥x轴,
∴点D纵坐标和点B纵坐标相同,
设D(x,2),
∵点B(4,2),BD=2,且点B在点D右边,
∴4﹣x=,
∴x=,
∴D(,2),
∴k=5,
∴所求反比例函数表达式为:y=;
∵点F在线段AB上,设F(4,y),
将点F坐标代入反比例函数表达式,得y=,
∴点F的坐标为(4,);
(2)DF∥AC,理由如下:
∵F(4,),B(4,2),
∴BF=,
又BC=4,AB=2,BD=,
∴
又∵∠B=∠B,
∴△BDF∽△BCA,
∴∠BDF=∠BCA.
∴DF∥AC;
(3)存在,M的坐标为(,)或(,,).理由如下:
①当∠MDN=90°时,
过点D作y轴平行线,过M、N分别作x轴的平行线,与过点D的y轴平行线交于点G、H,
∵△MDN是等腰直角三角形,
∴DM=ND,∠MDN=90°,
∴∠MDG+∠NDH=90°,
又∠MDG+∠DMG=90°,
∴∠DMG=∠NDH,
又∠G=∠H=90°,
∴△DMG≌△NDH(AAS),
∴NH=DG,
∵D(,2),
∴H的横坐标为,
∴NH=DG=,
设M(x,y),则点G的纵坐标为y,
DG=y﹣2=,
∴y=,
∴x=,
∴点M的坐标为(,);
②当∠DMN=90°时,
过点M作x轴平行线交y轴于点P,过D分别作y轴的平行线,与过点M的x轴平行线交于点Q,
∵△MDN是等腰直角三角形,
∴MN=DM,∠DMN=90°,
∴∠PMN+∠QMD=90°,
又∠PMN+∠PNM=90°,
∴∠PNM=∠QMD,
又∠MPN=∠Q=90°,
∴△MPN≌△DQM(AAS),
∴PM=QD,
设M(x,y),则点Q的纵坐标为y,
∴PM=x,QD=y﹣2,
∴x=y﹣2,
又y=,
∴=x+2,
解得:x=(舍去负值),
∴y=,
∴M(,,),
综上M的坐标为(,)或(,,).
19.(1)解:如图(1),过点B作EF⊥y轴,过点A作AE⊥EF于E,过点C作CF⊥EF于F,
则∠EAB+∠ABE=90°,
∵∠ABC=90°,
∴∠FBC+∠ABE=90°,
∴∠EAB=∠FBC,
在△BAE和△CBF中,
,
∴△BAE≌△CBF(AAS),
∴CF=BE=2,AE=BF,
设点C的坐标为(a,﹣1),则点A的坐标为(﹣2,a﹣3),
∵点A,C在反比例函数y=的图象上,
∴a×(﹣1)=﹣2×(a﹣3),
解得,a=6,
∴k=6×(﹣1)=﹣6;
(2)证明:如图(2),延长DC至点H,使CH=EA,连接BH,
∵直线BF的解析式为y=x+b,
∴∠EOF=45°,
∵∠ABC=90°,
∴∠ABE+∠CBF=45°,
在△ABE和△CBH中,
,
∴△ABE≌△CBH(SAS),
∴∠CBH=∠ABE,BF=BH,
∴∠FBH=∠CBH+∠CBF=45°,
∴∠EBF=∠HBF,
在△EBF和△HBF中,
,
∴△EBF≌△HBF(SAS),
∴EF=FH=AE+FC,
∴△DEF的周长=DE+EF+DF=DA+DC=2×=4.
20.解:(1)∵OB=2,AB=3,
∴点A的坐标是(2,3),
把A(2,3)代入y=得:3=,
∴k=6.
(2)∵点E恰好是DC的中点,
∴点E的纵坐标是.
当y=时,=,
解得:x=4,
∴点E的坐标是(4,).
①设直线AE的解析式是y=kx+b(k≠0),
将A(2,3),E(4,)代入y=kx+b得:,
解得:,
∴直线AE的解析式是y=﹣x+.
②当y=0时,﹣x+=0,解得:x=6,
∴点M的坐标为(0,6).
观察函数图象可知:在第一象限内,当0<x<2或4<x<6时,反比例函数图象在一次函数图象上方,
∴在第一象限内,当0<x<2或4<x<6时,反比例函数的函数值大于直线AE对应函数的函数值.
③AN=ME,理由如下:
延长DA交y轴于点F,如图所示.
则AF⊥y轴,AF=2,点F的坐标是(0,3),OF=3.
当x=0时,y=﹣×0+=,
∴点N的坐标为(0,),
∴NF=﹣3=,
∴AN===;
当y=0时,﹣x+=0,解得:x=6,
∴点M的坐标为(6,0),
∴CM=6﹣4=2,
∴ME===.
∴AN=ME.
21.解:(1)∵点B的坐标为(4,3),
∴OC=AB=3,OA=BC=4.
∵BD=1,
∴AD=2,
∴点D的坐标为(4,2).
∵反比例函数y=(x>0)的图象过点D,
∴k=4×2=8,
∴反比例函数的关系式为y=.
当y=3时,3=,解得:x=,
∴点E的坐标为(,3).
(2)在图2中,作点D关于x轴的对称点D′,连接D′E交x轴于点P,连接PD,此时PD+PE取得最小值,最小值为D′E.
∵点D的坐标为(4,2),
∴点D′的坐标为(4,﹣2).
又∵点E的坐标为(,3),
∴D′E==.
∵BE=4﹣=,BD=1,
∴DE==,
∴△PDE周长的最小值=D′E+DE=+=.
(3)在图3中,过点P作PF⊥OD于点F,则△PDF为等腰直角三角形.
∵OA=4,AD=2,
∴OD==2.
设AP=m,则OP=4﹣m,
∴PD==.
∵△PDF为等腰直角三角形,
∴DF=PF=PD=,
∴OF=OD﹣DF=2﹣.
∵OF2+PF2=OP2,即(2﹣)2+()2=(4﹣m)2,
整理得:3m2+16m﹣12=0,
解得:m1=,m2=﹣6(不合题意,舍去),
∴OP=4﹣m=.
1.已知反比例函数y=的图象经过点A(2,3).
(1)求该反比例函数的表达式;
(2)如图,在反比例函数y=的图象上点A的右侧取点C,过点C作x轴的垂线交x轴于点H,过点A作y轴的垂线交直线CH于点D.
①过点A,点C分别作x轴,y轴的垂线,两线相交于点B,求证:O,B,D三点共线;
②若AC=2OA,求证:∠AOD=2∠DOH.
2.定义:有一组对边平行,有一个内角是它对角的一半的凸四边形叫做半对角四边形,如图1,直线l1∥l2,点A,D在直线l1上,点B,C在直l2上,若∠BAD=2∠BCD,则四边形ABCD是半对角四边形.
(1)如图2,点E是矩形ABCD的边AD上一点,AB=1,AE=2.若四边形ABCE为半对角四边形,求AD的长:
(2)如图3,以?ABCD的顶点C为坐标原点,边CD所在直线为x轴,对角线AC所在直线为y轴,建立平面直角坐标系.点E是边AD上一点,满足BC=AE+CE.求证:四边形ABCE是半对角四边形;
(3)在(2)的条件下,当AB=AE=2,∠B=60°时,将四边形ABCE向左平移a(a>0)个单位后,恰有两个顶点落在反比例函数y=的图象上,求k的值.
3.如图,正比例函数y=x和反比例函数y=(x>0)的图象都经过点B(a,6),过点B且平行于x轴的直线交y轴于A,点C在AB的延长线上,CD∥y轴交反比例函数图象于D,连接CO,DO.
(1)求反比例函数的表达式;
(2)若∠ABO=∠OCD,求四边形OBCD的面积.
4.在平面直角坐标系xOy中,函数y=(x>0)的图象与直线y=x+1交于点A(2,m).
(1)求k、m的值;
(2)横、纵坐标都是整数的点叫做整点.已知点P(n,0),过点P作平行于y轴的直线,交直线y=x+1于点B,交函数y=(x>0)的图象于点C.将函数y=(x>0)的图象在点A、C之间的部分与线段AB、DC所围成的区域内部(不包括边界)记作图形G.
①当n=4时,直接写出图形G内的整点坐标;
②若图形G内恰有2个整点,直接写出n的取值范围.
5.如图:在平面直角坐标系中,菱形ABCD的顶点D在y轴上,A,C两点的坐标分别为(2,0),(2,m),直线CD:y1=ax+b与双曲线:y2=交于C,P(﹣4,﹣1)两点.
(1)求双曲线y2的函数关系式及m的值;
(2)判断点B是否在双曲线上,并说明理由;
(3)当y1>y2时,请直接写出x的取值范围.
6.如图,正方形OABC的边长为4,点A,C分别在x轴,y轴的正半轴上,双曲线:y=(x>0)与BC,AB分别交于点M,N,且BM=AN.
(1)求k的值.
(2)若点P在双曲线:y=(x>0)上正方形OABC内部一动点,
过点P作y轴的垂线,分别交OC、AB于点D、E.过点P作x轴的垂线,分别交OA、BC于点G、F.
①当点P在对角线OB上时.求△BEF的周长;
②随着点P的运动,△BEF的周长是否为定值?请说明理由.
7.如图,一次函数y=mx+6(m≠0)的图象经过点B(﹣6,0),与y轴交于C点,与反比例函数y=(x>0)的图象交于点A.连接OA,且△AOC的面积为6.
(1)求一次函数和反比例函数的解析式.
(2)结合图象直接写出当x>0时,mx+6<的解集;
(3)设点E是反比例函数y=(x>0)的图象上一点,点F是直线AB上一点,若以点O,E,C,F为顶点的四边形是平行四边形,求出点F的坐标.
8.如图在平面直角坐标系中,等腰Rt△AOB的斜边OB在x轴正半轴上,直线y=3x﹣4经过等腰Rt△AOB的直角顶点A,交y轴于C点,双曲线y=也经过A点.
(1)求点A的坐标和k的值;
(2)过点B作BQ⊥x轴交双曲线于点Q,连接AQ,过点A作AP⊥AQ交x轴于点P,连接PQ,求证:△APQ是等腰直角三角形,并求出此时点Q的坐标.(请根据题意自行画图)
9.如图,在平面直角坐标系中,点B的坐标为(6,4),反比例函数y=(x>0)的图象交矩形OABC的边BC,AB于D、E两点,连接DE,AC.
(1)当点D是BC的中点时,k=
,点E的坐标为
;
(2)设点D的横坐标为m.
①请用含m的代数式表示点E的坐标,
②求证:DE∥AC.
10.如图,已知一次函数y=kx+b的图象与反比例函数的图象交于A、B两点,A点的坐标是(﹣2,1),B点的坐标是(1,n).
(1)求出两个函数解析式;
(2)在x轴正半轴上是否存在点P,使△ABP为等腰三角形?若存在,求P点坐标;若不存在,请说明理由.
(3)直接写出满足的x的取值范围.
11.已知平面直角坐标系中,直线AB与反比例函数y=(x>0)的图象交于点A(1,3)和点B(3,n),与x轴交于点C,与y轴交于点D.
(1)求反比例函数的表达式及n的值;
(2)将△OCD沿直线AB翻折,点O落在第一象限内的点E处,EC与反比例函数的图象交于点F.
①请求出点F的坐标;
②将线段BF绕点B旋转,在旋转过程中,求线段OF的最大值和最小值.
12.如图,直线AC与函数y=﹣的图象相交于点A(﹣1,m),与x轴交于点C(5,0).
(1)求m的值及直线AC的解析式;
(2)直线AE在直线AC的上方,满足∠CAE=∠CAO,求直线AE的解析式;
(3)若D是线段AC上一点将OD绕点O逆时针旋转90°得到OD',点D'恰好落在函数y=﹣的图象上,求点D的坐标.
13.如图,直线y=x,与反比例函数y=在第一象限内的图象相交于点A(m,3).
(1)求该反比例函数的表达式;
(2)将直线y=x沿y轴向上平移,与反比例函数在第一象限内的图象相交于点B,与y轴交于点C,若,连接AB、OB.请判断AB与OA的位置关系,并说明理由;
(3)在(2)的条件下,在射线OA上是否存在一点P,使△PAB与△BAO相似,若存在,请直接写出P点坐标;不存在,请说明理由.
14.如图,在平面直角坐标系中已知四边形ABCD为菱形,且A(0,3),B(﹣4,0).
(1)求过点C的反比例函数表达式;
(2)设直线l与(1)中所求函数图象相切,且与x轴,y轴的交点分别为M,N,O为坐标原点.求证:△OMN的面积为定值.
15.模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
建立函数模型
设矩形相邻两边的长分别为x,y,由矩形的面积为4,得xy=4,即y=;由周长为m,得2(x+y)=m,即y=﹣x+满足要求的(x,y)应是两个函数图象在第一象限内交点的坐标.
作函数图象
(1)①当反比例y=(x>0)的图象与直线y=﹣x+有唯一交点(2,2)时,周长m的值为
;
②交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
解决问题
(2)若能生产出面积为4的矩形模具,则周长m的取值范围为
.
16.如图,一次函数y=﹣x+4与反比例函数y=(x>0)的图象在第一象限交于M,N两点,P是MN上一个动点(点P不与点M,N重合),过点P作PA⊥y轴,PB⊥x轴,垂足为A,B,交反比例函数于点D,点C.
(1)当AP=3AO时,求点D的坐标;
(2)连接AB,CD,若D是AP的中点,试判断AB与CD的位置关系,并说明理由;
(3)点P在运动过程中,AB是否具有最小值,若有,求出最小值;若没有,请说明理由.
17.已知:如图,双曲线y=(k≠0)与直线y=mx(m≠0)交于A(,3)、B两点,将直线AB向下平移n个单位,平移后的直线与双曲线在第一象限的分支交于点C,点D是x轴上一动点.
(1)求双曲线和直线的函数表达式;
(2)连接AD,当点C是线段AD中点时,求n的值;
(3)若点E是双曲线上任意一点,当△ADE是以AE为斜边的直角三角形,且∠DAE=30°时,求点E的坐标.
18.如图,在平面直角坐标系中,矩形ABCO的顶点A、C分别在x轴和y轴的正半轴上,顶点B的坐标为(4,2),双曲线y=(x>0)交BC于点D,交AB于点F,其中BD=.
(1)求反比例函数y=的表达式及F点坐标;
(2)判断DF与AC的位置关系,并说明理由;
(3)点N在y轴正半轴上,反比例函数图象上是否存在一点M,使△DMN是以DM为直角边的等腰直角三角形,若存在,直接写出点M的坐标;若不存在,请说明理由.
19.在平面直角坐标系中,正方形ABCD的位置如图(1)所示,且点A,C在反比例函数y=的图象上,已知点A的横坐标为﹣2,点C的纵坐标为﹣1.
(1)求k的值.
(2)如图(2),AD交y轴于点E,过点B的直线y=x+b交CD于点F,连接EF.求证:△DEF的周长为定值.
20.如图,在平面直角坐标系中,矩形ABCD的顶点B、C在x轴上,A、D在第一象限,反比例函数y=(x>0)的图象经过点A,交CD于点E,OB=2,AB=3.
(1)求k的值;
(2)若点E恰好是DC的中点.
①求直线AE的函数解析式;
②根据图象回答,在第一象限内,当x取何值时,反比例函数的函数值大于直线AE对应函数的函数值?
③若直线AE与x轴交于点M,与y轴交于点N,请你判断线段AN与线段ME的大小关系,并说明理由.
21.如图1,矩形OABC的顶点A、C分别落在x轴、y轴的正半轴上,点B(4,3),反比例函数y=(x>0)的图象与AB、BC分别交于D、E两点,BD=1,点P是线段OA上一动点.
(1)求反比例函数关系式和点E的坐标;
(2)如图2,连接DE、PE、PD,求△PDE周长的最小值;
(3)如图3,当∠PDO=45°时,求线段OP的长.
参考答案
1.(1)解:∵反比例函数y=的图象经过点A(2,3),
∴3=,
∴m=6,
∴反比例函数的解析式为y=.
(2)证明:①过点A作AM⊥x轴于M,过点C作CN⊥y轴于N,AM交CN于点B,连接OB.
∵A(2,3),点C在y=的图象上,
∴可以设C(m,),则B(2,),D(m,3),
∴∠BOM=∠DOH,
∴O,B,D共线.
②设AC交BD于J.
∵AD⊥y轴,CB⊥y轴,
∴AD∥CB,
∵AM⊥x轴,DH⊥x轴,
∴AB∥CD,
∴四边形ABCD是平行四边形,
∵∠ADC=90°,
∴四边形ABCD是矩形,
∴AJ=JC=JD=JB,
∵AC=2OA,
∴AO=AJ,
∴∠AOJ=∠AJO,
∵∠AJO=∠JAD+∠JDA,
∵AD∥OB,
∴∠DOH=∠ADJ,
∵JA=JD,
∴∠JAD=∠ADJ,
∴∠AOD=2∠ADJ=∠DOH.
2.解:(1)∵四边形ABCE为半对角四边形,
∴∠BCE=45°,
∴∠DEC=∠DCE=45°,
∴CD=DE=1,
∴AD=AE+DE=3.
(2)证明∵四边形ABCD为平行四边形,
∴BC∥AD,BC=AD=AE+ED=AE+CE,
∴CE=ED,
∴∠AEC=2∠EDC=2∠B,
又∵AE∥BC,
∴四边形ABCE是半对角四边形;
(3)由题意,可知:点A的坐标为(0,6),点B的坐标为(2,6),点E的坐标为(﹣,3).
(i)当点A,E向左平移a(a>0)个单位后落在反比例函数的图象上时,﹣a?6=(﹣﹣a)?3,
解得:a=,
∴k=﹣6a=﹣6;
(ii)当点B,E向左平移a(a>0)个单位后落在反比例函数的图象上时,(2﹣a)?6=(﹣﹣a)?3,
解得:a=5,
∴k=3(﹣﹣a)=﹣18.
综上所述:k的值为为﹣6或﹣18.
3.解:(1)∵正比例函数y=x和反比例函数y=(x>0)的图象都经过点B(a,6),
∴令y=6,则,
∴x=4,
∴B(4,6),
∴k=24,
∴反比例函数的表达式为;
(2)∵CD∥y轴,
∴∠OCD=∠AOC,
又∠ABO=∠OCD,
∴∠AOC=∠ABO,
∵∠OAC=∠BAO=90°,
∴△OAC∽△BAO,
∴,
∴AO2=AB?AC,
∵B的坐标为(4,6),且AB∥x轴,
∴AO=6,AB=4,
∴36=4AC,
∴AC=9,
∴C(9,6),
∵CD∥y轴,
∴D(9,),
∴,
S四边形OBCD=S△BOC+S△COD==30.
4.解:(1)∵点A(2,m)在直线y=x+1上,
∴m=×2+1=2.
∴A(2,2).
∵点A(2,2)在函数y=(x>0)的图象上,
∴k=4.
(2)①当n=4时,点B(4,3),C(4,1).
∵整点在图形G的内部,
∴2<x<4,且x为整数,
∴x=3.
当x=3时,y=x+1=×3+1=,
y==.
∴.
∵y为整数,
∴y=2.
∴图形G内的整点坐标为(3,2).
②由①知当x=3时,,此时整点为(3,2)共1个;
当x=4时,1<y<3,此时整点为(4,2),1个;
当x=5时,,此时整点有(5,1),(5,2),(5,3),3个;
∵图形G恰好有2个整点,
∴4<n<5.
当x=1时,1.5<y<4,此时整点为(1,2),(1,3),2个,
∴0<n<1.
综上所述,n的取值范围为:4<n<5或0<n<1.
5.解:(1)
连接AC,BD相交于点E,
∵四边形ABCD是菱形,
∴DE=BE,AE=CE,AC⊥BD,
∵A(2,0),C(2,m),
∴E(2,m),AC∥y轴,
∴BD⊥y轴,
∴点D(0,m),B(4,m),
∵点C(2,m),D(0,m),P(﹣4,﹣1)在直线CD上,
∴,
∴,
∴点C(2,2),
∵点C在双曲线y2=上,
∴k=2×2=4,
∴双曲线的函数关系式为y2=;
(2)由(1)知,m=2,B(4,m),
∴B(4,1),
由(1)知双曲线的解析式为y2=;
∵4×1=4,
∴点B在双曲线上;
(3)由(1)知C(2,2),
由图象知,当y1>y2时的x值的范围为﹣4<x<0或x>2.
6.解:(1)∵正方形OABC的边长为4,
∴OA=OC=BC=4,
设点M(m,4),
∴CM=m,
∴BM=BC﹣CM=4﹣m,
∵AN=BM,
∴AN=4﹣m,
∴N(4,4﹣m),
∵点M,N都在双曲线:y=(x>0)上,
∴k=4m=4(4﹣m),
∴m=2,k=8;
(2)由(1)知,k=8,
∴双曲线的解析式为y=,M(2,4),N(4,2),
∵点P在双曲线:y=(x>0)上正方形OABC内部一动点,
∴设P(n,),
①∵正方形OABC的边长为4,
∴B(4,4),
∴直线OB的解析式为y=x,
∵点P在对角线OB上,
∴n=,
∴n=2或n=﹣2(舍),
∴P(2,2),
∵PD⊥y轴,PG⊥x轴,
∴E(2,4),F(4,2),
∴BF=4﹣2,BE=4﹣2,EF=BE=4﹣4,
∴△BEF的周长为4﹣2+4﹣2+4﹣4=4;
②随着点P的运动,△BEF的周长是定值,为4,
理由:∵PD⊥y轴,PG⊥x轴,
∴F(n,4),E(4,),
∴BF=4﹣n,BE=4﹣,
根据勾股定理得,EF====n+﹣4,
∴△BEF的周长为4﹣n+4﹣+n+﹣4=4,
即随着点P的运动,△BEF的周长是定值,其值为4.
7.解:(1)∵一次函数y=mx+6(m≠0)的图象经过点B(﹣6,0),
∴﹣6m+6=0,得m=1,
∴一次函数解析式为y=x+6;
当x=0时,y=6,
∴CO=6,
∵△AOC的面积为6.
∴,
∴xA=2,
当x=2时,y=x+6=8,
∴点A坐标(2,8),
∵反比例函数y=(x>0)的图象经过点A,
∴k=16,
∴反比例函数的解析式为:y=;
(2)结合图象可知当x>0时,mx+6<的解集是0<x<2;
(3)①当CO为边时,如图1,EF∥CO且EF=CO,
设点E坐标为(m,),则点F的坐标为(m,m+6),
∴EF=|﹣m﹣6|,
∴|﹣m﹣6|=6,
当﹣m﹣6=6时,
解得m=4或﹣4(﹣4舍去)此时点F坐标为(4,10);
当﹣m﹣6=﹣6时,
解得m=2﹣6或﹣2﹣6(负值舍去),此时点F坐标为(2﹣6,2);
②当CO为对角线时,如图2,则CO与FE互相平分,
设点E坐标为(m,),点F的坐标为(n,n+6),
由中点坐标公式得,
解得m=4,n=﹣4,此时点F坐标为(﹣4,2),
综上.点N坐标为(4,10)或(2﹣6,2)或(﹣4,2).
8.解:(1)过点A分别作AM⊥y轴于M点,AN⊥x轴于N点,
∵△AOB是等腰直角三角形,
∴AM=AN.
设点A的坐标为(a,a),
∵点A在直线y=3x﹣4上,
∴a=3a﹣4,
解得a=2,
则点A的坐标为(2,2),
∵双曲线y=也经过A点,
∴k=2×2=4;
(2)在△AOP与△ABQ中,
∵∠OAB﹣∠PAB=∠PAQ﹣∠PAB,
∴∠OAP=∠BAQ,
在△AOP和△ABQ中,
,
∴△AOP≌△ABQ(ASA),
∴AP=AQ,
∴△APQ是所求的等腰直角三角形.
∵点A的坐标为(2,2),△OAB为等腰直角三角形,
则OB=4,故B(4,0),
故点Q的横坐标为4,
由(1)知,反比例函数表达式为y=,
当x=4时,y==1,
故Q(4,1).
9.解:(1)∵点D是BC的中点,则点D(3,4),
将点D(3,4)代入反比例函数表达式得:4=,解得k=12;
故反比例函数的表达式为y=,
当x=6时,y===2,
故点E的坐标为(6,2),
故答案为:12,(6,2);
(2)①由题意得,点D的坐标为(m,4),
则k=4m,
则反比例函数表达式为y=,
当x=6时,y==,
即点E的坐标为(6,);
②由①知,BD=6﹣m,BE=4﹣,
∴=1﹣m,=1﹣m=,
∴DE∥AC.
10.解:(1)∵反比例函数y=的图象过点A(﹣2,1),
∴m=﹣2×1=﹣2,
∴反比例函数的解析式为y=﹣,
∵反比例函数y=﹣的图象过点B(1,n),
∴﹣2=1×n,
∴n=﹣2,
∴B(1,﹣2),
∵一次函数y=kx+b的图象过A,B两点,
∴,
解得k=﹣1,b=﹣1,
∴一次函数的解析式为y=﹣x﹣1;
(2)设点P(m,0)(m>0),
∵A(﹣2,1),B(1,﹣2),
∴AB2=(﹣2﹣1)2+[1﹣(﹣2)]2=18,AP2=(m+2)2+1=m2+4m+5,BP2=(m﹣1)2+4=m2﹣2m+5,
∵△ABP为等腰三角形,
∴①当AP=AB时,AP2=AB2,
∴m2+4m+5=18,
∴m=﹣2﹣(舍)或m=﹣2+,
∴P(﹣2+,0),
②当AP=BP时,AP2=BP2,
∴m2+4m+5=m2﹣2m+5,
∴m=0(舍),
③当AB=BP时,AB2=BP2,
∴m2﹣2m+5=18,
∴m=1﹣(舍)或m=1+,
∴P(1+,0),
即满足条件的点P的坐标为(﹣2+,0)或(1+,0).
(3)∵一次函数的解析式为y=﹣x﹣1,其图象与x轴交于点C,
∴点C的坐标为(﹣1,0),
∵CA(﹣2,1),
∴0<kx+b<的x的取值范围是﹣2<x<﹣1.
11.解:(1)将A(1,3)代入y=(x>0)中得,
3=,
解得:k=3,
∴反比例函数解析式为:y=,
∵B(3,n)在反比例函数y=上,
∴n==1;
(2)①设直线DC的解析式为:y=kx+b(k≠0),图象经过点A(1,3)、B(3,1),将其代入得:
,
解得:,
∴直线DC的解析式为:y=﹣x+4,
令y=0,则0=﹣x+4,解得x=4,
令x=0,则y=4,
∴OD=OC=4,
又∵将△OCD沿直线AB翻折,点落在第一象限内的点E处,
∴DE=4,
即F点的横坐标为4,且在反比例函数的图象上,
∴当x=4时,y=,
故F点坐标为(4,);
②由①可知,B(3,1),F(4,),
∴BF==,OB==,
由题意可知;线段BF绕点B旋转过程中,F始终在以B点为圆心,BF为半径的圆上,
情况一:当BF旋转到线段OB上时,如图所示,OF1为线段OF的最小值,
∴OFmin=OB﹣BF1=,
情况二:当BF旋转到线段OB的延长线上时,如图所示,OF2为线段OF的最大值,
∴OFmax=OB+BF2=,
综上,线段BF绕点B在旋转过程中,线段OF的最大值为,最小值为.
12.解:(1)将点A(﹣1,m)代入函数y=﹣中得:
m==6,
设直线AC的解析式为y=kx+b(k≠0),经过A(﹣1,6),C(5,0)两点,将其代入得:
,
解得:,
∴直线AC的解析式为:y=﹣x+5;
(2)在AE上截取AF,使得AF=AO,则:
在△ACO和△ACF中,
,
∴△ACO≌△ACF(SAS),
∴AF=AO==,
在y=﹣x+5中,令y=0,则x=5,
∴OC=CF=5
设F(a,b),
∴AF=,FC=,
∴,
解得:或(舍去),
∴点F坐标为(5,5),
设直线AE的解析式为:y=k'x+b'(k'≠0),经过点F(5,5),点A(﹣1,6),将其代入得:
,
解得:,
∴直线AE的解析式:y=﹣,
(3)设OD绕点O逆时针旋转90°得到OD',则∠DOD'=90°,过点D作DN⊥x轴交于点N,过点D'作D'M⊥x轴交于点M,
∵∠D'OM+∠DON=90°,∠D'OM+∠OD'M=90°,
在△D'OM和△ODN中,
,
∴△D'OM≌△ODN(AAS),
∴DN=OM,NO=D'M,
设D(d,﹣d+5),则:DN=OM=﹣d+5,NO=D'M=d,
∵点D'在第二象限,
∴D’(d﹣5,d)且在y=上,
∴d=﹣,
解得:d1=2,d2=3,
经检验符合题意,
∴D坐标为(2,3)或(3,2).
13.解:(1)∵点A(m,3)在直线y=x,
∴3=m,
∴m=3,
∴点A(3,3),
∵点A(3,3)在反比例函数y=上,
∴k=3×3=9,
∴y=;
(2)OA⊥AB,理由如下:
如图,作BE⊥y轴于E,AF⊥y轴于F.
∴∠BEO=∠AFO=90°,
∵BC∥AO,
∴∠ECB=∠FOA,
∴△BCE∽△AOF,
∴=,
∴=,
∴BE=,
∴B(,9),
又∵A(3,3),
∴OA2=36,OB2=84,AB2=48,
∴OA2+AB2=OB2,
∴∠OAB=90°,
∴OA⊥AB.
(3)如图,①当△APB∽△ABO时,=,
由(2)知,AB=4,OA=6,即
=,
∴AP=8,
∵OA=6,
∴OP=14,
过点A作AH⊥x轴于H,
∵A(3,3),
∴OH=3,AH=3,
在Rt△AOH中,
∴∠AOH=30°.
过点P作PG⊥x轴于G,
在Rt△APG中,∠POG=30°,OP=14,
∴PG=7,OG=7
,
∴P(7,7).
②当△PAB∽△OAB时,==1.
∴AP=OA,即A是OP的中点,
由(2)知,A(3,3),
∴P(6,6).
综上所述,符合条件的点P的坐标是(7,7)或(6,6).
14.(1)解:∵点A的坐标为(0,3),点B的坐标为(﹣4,0),
∴OA=3,OB=4.
在Rt△AOB中,OA=3,OB=4,
∴AB==5.
∵四边形ABCD为菱形,
∴BC∥y轴,且BC=AB=5,
∴点C的坐标为(﹣4,﹣5).
∵点C在反比例函数y=的图象上,
∴k=(﹣4)×(﹣5)=20,
∴过点C的反比例函数表达式为y=.
(2)证明:设直线l的解析式为y=mx+n(m≠0),
将y=mx+n代入y=得:mx+n=,
整理得:mx2+nx﹣20=0.
∵直线l与反比例函数y=的图象相切,
∴△=n2﹣4×m×(﹣20)=0,
∴n2=﹣80m.
当x=0时,y=m×0+n=n,
∴点N的坐标为(0,n);
当y=0时,mx+n=0,解得:x=﹣,
∴点M的坐标为(﹣,0).
∴S△OMN=|n|×|﹣|=||=40,
∴△OMN的面积为定值.
15.解:图象如下所示:
(1)①把点(2,2)代入y=﹣x+得:
2=﹣2+,
解得:m=8,
故答案是:8;
②由①知:0个交点时,0<m<8;2个交点时,m>8;1个交点时,m=8;
(2)联立y=和y=﹣x+并整理得:x2﹣mx+4=0,
△=m2﹣4×4≥0时,两个函数有交点,
解得:m≥8.
故答案是:m≥8.
16.解:设点P的坐标为(m,﹣m+4),则点A、B的坐标分别为(0,﹣m+4)、(m,0).
(1)当AP=3AO时,即m=3(﹣m+4),
解得m=3,
故点A的坐标为(0,1),
当y=1时,即1=,
解得x=1,
故点D的坐标为(1,1);
(2)∵D是AP的中点,故点D的坐标为(m,﹣m+4),
将点D的坐标代入反比例函数表达式并整理得:4﹣m=,
设直线AB的表达式为y=kx+b,则,解得,
即直线AB表达式中的k值为﹣;
同理可得,直线CD表达式中的k值为﹣,
故直线AB∥CD;
(3)有,理由:
由题意得,四边形OAPB为矩形,
则AB=OP===≥2,
故AB有最小值为2.
17.解:(1)将点A的坐标代入反比例函数表达式得:3=,解得k=3,
设直线AB的表达式为y=mx,将点A的坐标代入上式得:3=m,解得m=,
故反比例函数和直线AB的表达式分别为y=和y=x;
(2)平移后直线的表达式为y=x﹣n,
连接A、C、D,分别过点A、C作x轴的垂线,垂足分别为M、N,
∵AM∥CN,点C是线段AD中点,
故CN是△AMD的中位线,设点C的坐标为(a,),
则CN=AM,即=×3,解得a=2,
故点C的坐标为(2,),
将点C的坐标代入y=x﹣n得:=?2﹣n,
解得n=;
(3)过点A、E分别作x轴的垂线,垂足分别为H、N,
在Rt△ADE中,∠DAE=30°,则AD:DE=,
∵∠ADH+∠EDN=90°,∠EDN+∠DEN=90°,
∴∠ADH=∠DEN,
∴Rt△AHD∽Rt△DNE,
∴,
设点D的坐标为(t,0),点E的坐标为(b,),
则AH=3,DH=t﹣,DN=b﹣t,EN=,
即,
解得b=3或﹣,
故点E的坐标为(﹣,﹣3)或(3,1).
18.解:(1)∵四边形ABCD是矩形,
∴BC∥x轴,
∴点D纵坐标和点B纵坐标相同,
设D(x,2),
∵点B(4,2),BD=2,且点B在点D右边,
∴4﹣x=,
∴x=,
∴D(,2),
∴k=5,
∴所求反比例函数表达式为:y=;
∵点F在线段AB上,设F(4,y),
将点F坐标代入反比例函数表达式,得y=,
∴点F的坐标为(4,);
(2)DF∥AC,理由如下:
∵F(4,),B(4,2),
∴BF=,
又BC=4,AB=2,BD=,
∴
又∵∠B=∠B,
∴△BDF∽△BCA,
∴∠BDF=∠BCA.
∴DF∥AC;
(3)存在,M的坐标为(,)或(,,).理由如下:
①当∠MDN=90°时,
过点D作y轴平行线,过M、N分别作x轴的平行线,与过点D的y轴平行线交于点G、H,
∵△MDN是等腰直角三角形,
∴DM=ND,∠MDN=90°,
∴∠MDG+∠NDH=90°,
又∠MDG+∠DMG=90°,
∴∠DMG=∠NDH,
又∠G=∠H=90°,
∴△DMG≌△NDH(AAS),
∴NH=DG,
∵D(,2),
∴H的横坐标为,
∴NH=DG=,
设M(x,y),则点G的纵坐标为y,
DG=y﹣2=,
∴y=,
∴x=,
∴点M的坐标为(,);
②当∠DMN=90°时,
过点M作x轴平行线交y轴于点P,过D分别作y轴的平行线,与过点M的x轴平行线交于点Q,
∵△MDN是等腰直角三角形,
∴MN=DM,∠DMN=90°,
∴∠PMN+∠QMD=90°,
又∠PMN+∠PNM=90°,
∴∠PNM=∠QMD,
又∠MPN=∠Q=90°,
∴△MPN≌△DQM(AAS),
∴PM=QD,
设M(x,y),则点Q的纵坐标为y,
∴PM=x,QD=y﹣2,
∴x=y﹣2,
又y=,
∴=x+2,
解得:x=(舍去负值),
∴y=,
∴M(,,),
综上M的坐标为(,)或(,,).
19.(1)解:如图(1),过点B作EF⊥y轴,过点A作AE⊥EF于E,过点C作CF⊥EF于F,
则∠EAB+∠ABE=90°,
∵∠ABC=90°,
∴∠FBC+∠ABE=90°,
∴∠EAB=∠FBC,
在△BAE和△CBF中,
,
∴△BAE≌△CBF(AAS),
∴CF=BE=2,AE=BF,
设点C的坐标为(a,﹣1),则点A的坐标为(﹣2,a﹣3),
∵点A,C在反比例函数y=的图象上,
∴a×(﹣1)=﹣2×(a﹣3),
解得,a=6,
∴k=6×(﹣1)=﹣6;
(2)证明:如图(2),延长DC至点H,使CH=EA,连接BH,
∵直线BF的解析式为y=x+b,
∴∠EOF=45°,
∵∠ABC=90°,
∴∠ABE+∠CBF=45°,
在△ABE和△CBH中,
,
∴△ABE≌△CBH(SAS),
∴∠CBH=∠ABE,BF=BH,
∴∠FBH=∠CBH+∠CBF=45°,
∴∠EBF=∠HBF,
在△EBF和△HBF中,
,
∴△EBF≌△HBF(SAS),
∴EF=FH=AE+FC,
∴△DEF的周长=DE+EF+DF=DA+DC=2×=4.
20.解:(1)∵OB=2,AB=3,
∴点A的坐标是(2,3),
把A(2,3)代入y=得:3=,
∴k=6.
(2)∵点E恰好是DC的中点,
∴点E的纵坐标是.
当y=时,=,
解得:x=4,
∴点E的坐标是(4,).
①设直线AE的解析式是y=kx+b(k≠0),
将A(2,3),E(4,)代入y=kx+b得:,
解得:,
∴直线AE的解析式是y=﹣x+.
②当y=0时,﹣x+=0,解得:x=6,
∴点M的坐标为(0,6).
观察函数图象可知:在第一象限内,当0<x<2或4<x<6时,反比例函数图象在一次函数图象上方,
∴在第一象限内,当0<x<2或4<x<6时,反比例函数的函数值大于直线AE对应函数的函数值.
③AN=ME,理由如下:
延长DA交y轴于点F,如图所示.
则AF⊥y轴,AF=2,点F的坐标是(0,3),OF=3.
当x=0时,y=﹣×0+=,
∴点N的坐标为(0,),
∴NF=﹣3=,
∴AN===;
当y=0时,﹣x+=0,解得:x=6,
∴点M的坐标为(6,0),
∴CM=6﹣4=2,
∴ME===.
∴AN=ME.
21.解:(1)∵点B的坐标为(4,3),
∴OC=AB=3,OA=BC=4.
∵BD=1,
∴AD=2,
∴点D的坐标为(4,2).
∵反比例函数y=(x>0)的图象过点D,
∴k=4×2=8,
∴反比例函数的关系式为y=.
当y=3时,3=,解得:x=,
∴点E的坐标为(,3).
(2)在图2中,作点D关于x轴的对称点D′,连接D′E交x轴于点P,连接PD,此时PD+PE取得最小值,最小值为D′E.
∵点D的坐标为(4,2),
∴点D′的坐标为(4,﹣2).
又∵点E的坐标为(,3),
∴D′E==.
∵BE=4﹣=,BD=1,
∴DE==,
∴△PDE周长的最小值=D′E+DE=+=.
(3)在图3中,过点P作PF⊥OD于点F,则△PDF为等腰直角三角形.
∵OA=4,AD=2,
∴OD==2.
设AP=m,则OP=4﹣m,
∴PD==.
∵△PDF为等腰直角三角形,
∴DF=PF=PD=,
∴OF=OD﹣DF=2﹣.
∵OF2+PF2=OP2,即(2﹣)2+()2=(4﹣m)2,
整理得:3m2+16m﹣12=0,
解得:m1=,m2=﹣6(不合题意,舍去),
∴OP=4﹣m=.
