2021-2022学年九年级数学鲁教版(五四制)上册《1.3反比例函数的应用》同步优生辅导训练(word版附答案)
文档属性
| 名称 | 2021-2022学年九年级数学鲁教版(五四制)上册《1.3反比例函数的应用》同步优生辅导训练(word版附答案) |  | |
| 格式 | doc | ||
| 文件大小 | 325.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 20:20:53 | ||
图片预览


文档简介
2021年鲁教版九年级数学上册《1.3反比例函数的应用》同步优生辅导训练(附答案)
一、选择题
1.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A.
B.
C.
D.
2.如图过y轴一个动点M作x轴的平行线,交双曲线于点A,交双曲线于点B,点C、点D在x轴上运动,且始终保持DC=AB,则平行四边形ABCD的面积是( )
A.7
B.10
C.14
D.28
3.下列两个变量之间的关系为反比例关系的是( )
A.圆的周长与其半径的关系
B.平行四边形面积一定时,其一边长与这边上的高的关系
C.销售单价一定时,销售总价与销售数量的关系
D.汽车匀速行驶过程中,行驶路程与行驶时间的关系
4.为预防新冠病毒,某学校每周末用药熏消毒法对教室进行消毒,已知药物释放过程中,教室内每立方米空气中含药量y(mg)与时间t(h)成正比例;药物释放完毕后,y与t成反比例,如图所示.根据图象信息,下列选项错误的是( )
A.药物释放过程需要小时
B.药物释放过程中,y与t的函数表达式是y=t
C.空气中含药量大于等于0.5mg/m3的时间为h
D.若当空气中含药量降低到0.25mg/m3以下时对身体无害,那么从消毒开始,至少需要经过4.5小时学生才能进入教室
5.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A.不小于0.5m3
B.不大于0.5m3
C.不小于0.6m3
D.不大于0.6m3
6.某校对学生宿舍采取喷洒药物进行消毒,在对某宿舍进行消毒的过程中,先经过5min的集中药物喷洒,再封闭宿舍10min,然后打开门窗进行通风,室内每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(min)之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
A.经过5min集中喷洒药物,室内空气中的含药量最高达到10mg/m3
B.室内空气中的含药量不低于8mg/m3的持续时间达到了11min
C.此次消毒完全有效.(有效的标准为:当室内空气中的含药量不低于5mg/m3,且持续时间不低于35分钟)
D.当室内空气中的含药量低于2mg/m3时,对人体才是安全的,所以从室内空气中的含药量达到2mg/m3开始,需经过59min后,学生才能进入室内
7.某学校要种植一块面积为200m2的长方形草坪,要求两边长均不小于10m,则草坪的一边长y(单位:m)随另一边长x(单位:m)的变化而变化的图象可能是( )
A.B.C.D.
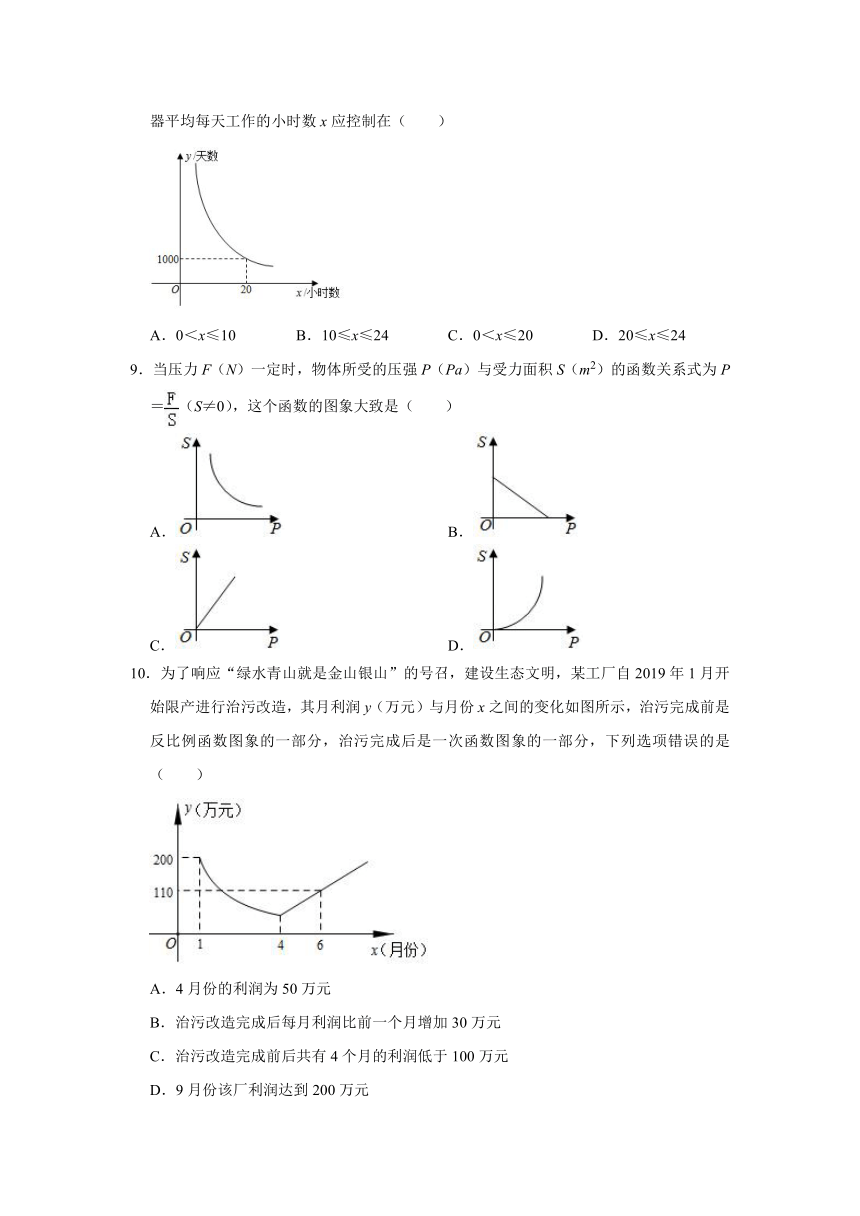
8.已知某品牌显示器的使用寿命为定值.这种显示器可工作的天数y与平均每天工作的小时数x是反比例函数关系,图象如图所示.如果这种显示器至少要用2000天,那么显示器平均每天工作的小时数x应控制在( )
A.0<x≤10
B.10≤x≤24
C.0<x≤20
D.20≤x≤24
9.当压力F(N)一定时,物体所受的压强P(Pa)与受力面积S(m2)的函数关系式为P=(S≠0),这个函数的图象大致是( )
A.
B.
C.
D.
10.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
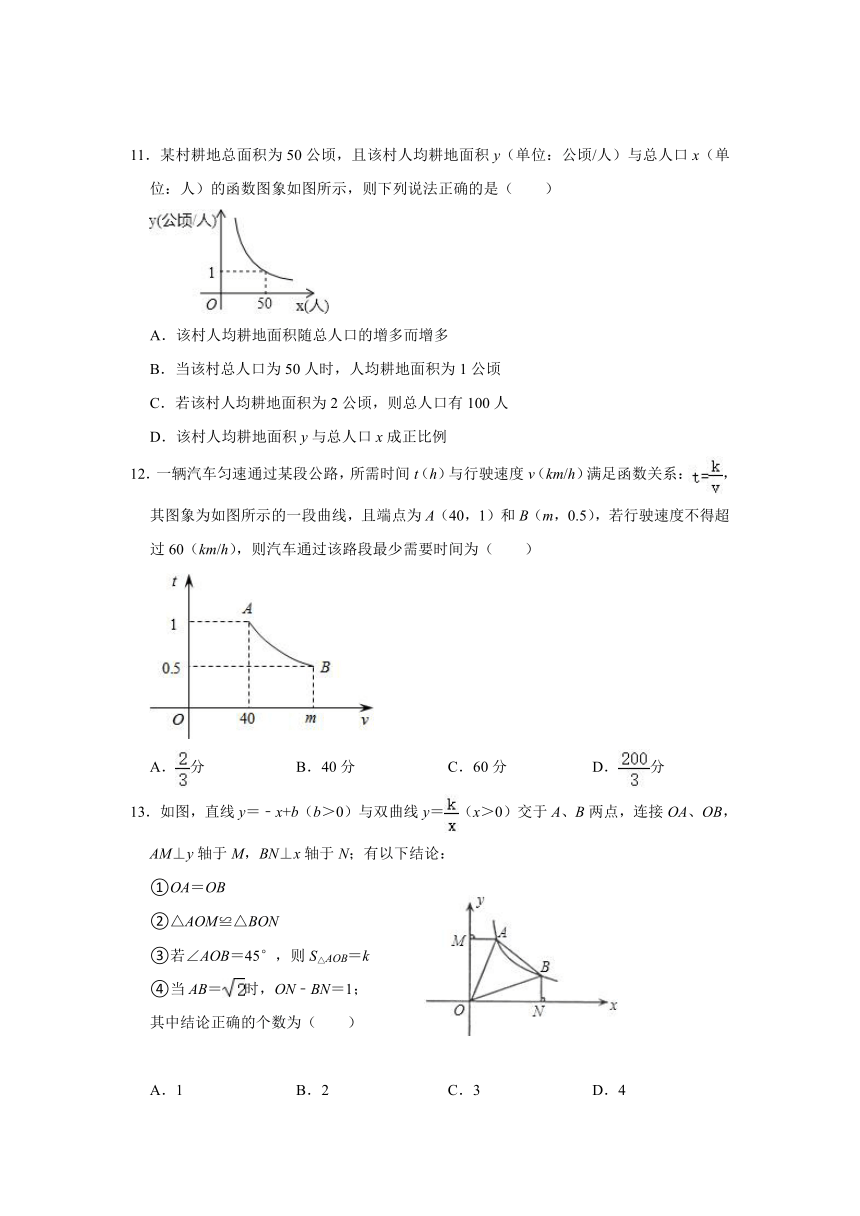
11.某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口有100人
D.该村人均耕地面积y与总人口x成正比例
12.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5),若行驶速度不得超过60(km/h),则汽车通过该路段最少需要时间为( )
A.分
B.40分
C.60分
D.分
13.如图,直线y=﹣x+b(b>0)与双曲线y=(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N;有以下结论:
①OA=OB
②△AOM≌△BON
③若∠AOB=45°,则S△AOB=k
④当AB=时,ON﹣BN=1;
其中结论正确的个数为( )
A.1
B.2
C.3
D.4
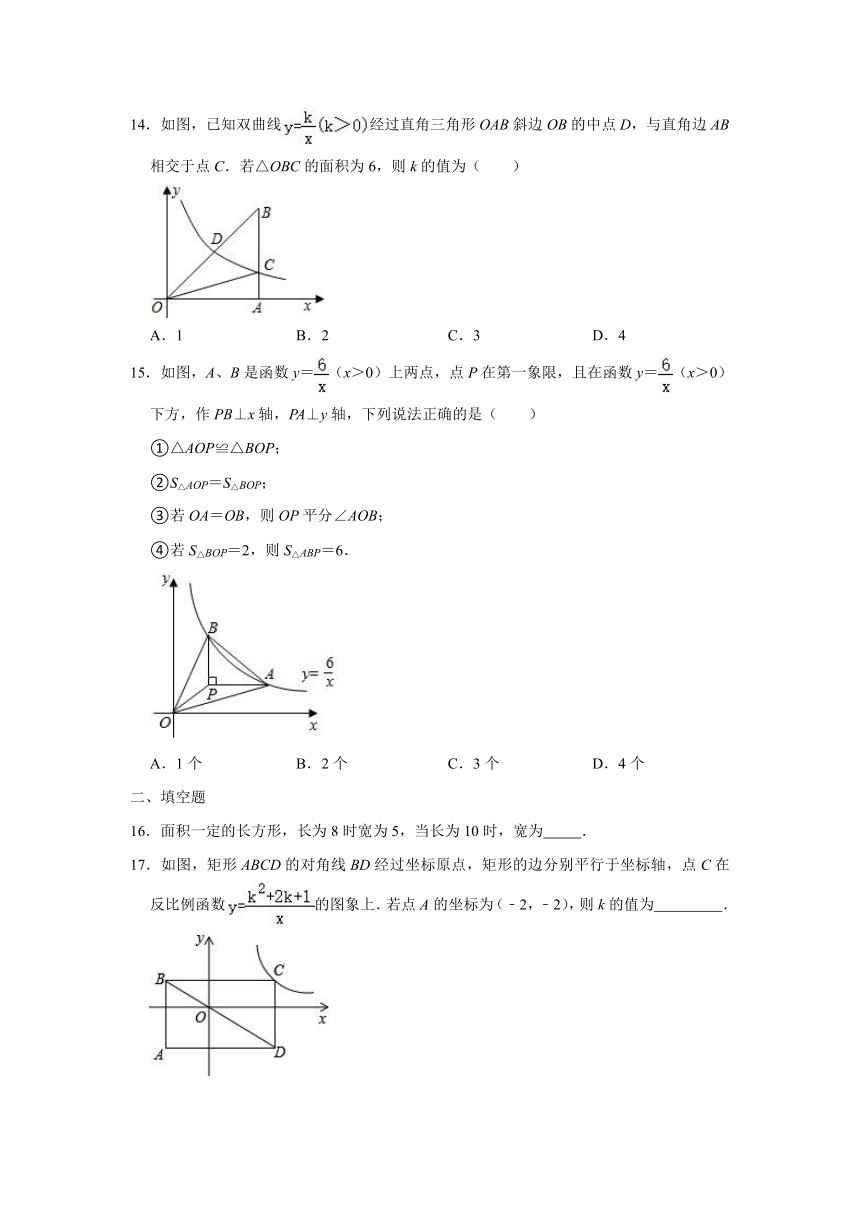
14.如图,已知双曲线经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为6,则k的值为( )
A.1
B.2
C.3
D.4
15.如图,A、B是函数y=(x>0)上两点,点P在第一象限,且在函数y=(x>0)下方,作PB⊥x轴,PA⊥y轴,下列说法正确的是( )
①△AOP≌△BOP;
②S△AOP=S△BOP;
③若OA=OB,则OP平分∠AOB;
④若S△BOP=2,则S△ABP=6.
A.1个
B.2个
C.3个
D.4个
二、填空题
16.面积一定的长方形,长为8时宽为5,当长为10时,宽为
.
17.如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数的图象上.若点A的坐标为(﹣2,﹣2),则k的值为
.
三、解答题
18.为了预防“流感”,某学校对教室采取药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y与x成反比例(如图所示).现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克.
(1)求药物燃烧时y关于x的函数关系式及其自变量x的取值范围;
(2)药物燃烧后y关于x的函数关系式是
;
(3)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回到教室.
19.通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当0≤x<10和10≤x<20时,图象是线段;当20≤x≤45时,图象是反比例函数的一部分.
(1)求点A对应的指标值;
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.
20.一辆客车从甲地出发前往乙地,平均速度v(千米/时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)求v与t的函数关系式及t值的取值范围;
(2)客车上午8时从甲地出发.
①客车需在当天14时40分至15时30分(含14时40分与15时30分)间到达乙地,求客车行驶速度v的范围;
②客车能否在当天12时30分前到达乙地?说明理由.
参考答案
1.解:设用电阻R表示电流I的函数解析式为I=,
∵过(2,3),
∴k=3×2=6,
∴I=,
故选:D.
2.解:设M的坐标为(0,m)(m>0),则直线AB的方程为:y=m,
将y=m代入y=﹣中得:x=﹣,∴A(﹣,m),
将y=m代入y=中得:x=,∴B(,m),
∴DC=AB=﹣(﹣)=,
过B作BN⊥x轴,则有BN=m,
则平行四边形ABCD的面积S=DC?BN=?m=14.故选:C.
3.解:A.圆的周长与其半径是正比例函数,故不符合题意;
B.平行四边形面积一定时,其一边长与这边上的高是反比例函数,故符合题意;
C.销售单价一定时,销售总价与销售数量是正比例函数,故不符合题意;
D.汽车匀速行驶过程中,行驶路程与行驶时间是正比例函数,故不符合题意.
故选:B.
4.解:设正比例函数解析式是y=kt,
反比例函数解析式是y=,
把点(3,)分别代入反比例函数解析式得:=,
解得:m=,
∴反比例函数解析式是y=,
当y=1时,代入上式得t=,
把t=时,y=1代入正比例函数解析式是y=kt得:k=,
∴正比例函数解析式是y=t,
A.由图象知,y=1时,t=,即药物释放过程需要小时,故A不符合题意;
B.药物释放过程中,y与t的成正比例,函数表达式是y=t,故B不符合题意;
C.把y=0.5mg/m3分别代入y=t和y=得,0.5=t1和0.5=,
解得:t1=和t2=3,
∴t2﹣t1=,
∴空气中含药量大于等于0.5mg/m3的时间为h;故C不符合题意;
<0.25,
解得t>6,
所以至少需要经过6小时后,学生才能进入教室,故D符合题意,
故选:D.
5.解:设函数解析式为P=,
∵当V=1.5m3时,p=16000Pa,
∴k=Vp=24000,
∴p=,
∵气球内的气压大于40000Pa时,气球将爆炸,
∴≤40000,
解得:V≥0.6,即气球的体积应不小于0.6m3.
故选:C.
6.解:A、由图象可得此选项正确,不符合题意.
B、由题意x=4时,y=8,故室内空气中的含药量不低于8mg/m3的持续时间达到了11min,正确,不符合题意;
C、y=5时,x=2.5或24,24﹣2.5=21.5<35,故本选项错误,符合题意;
D、当x≤5时,函数关系式为y=2x,y=2时,x=1;当x>15时,函数关系式为y=,y=2时,x=60;60﹣1=59,故当室内空气中的含药量低于2mg/m3时,对人体才是安全的,所以从室内空气中的含药量达到2mg/m3开始,需经过59min后,学生才能进入室内,正确.不符合题意,
故选:C.
7.解:∵草坪面积为200m2,
∴x、y存在关系y=,
∵两边长均不小于10m,
∴x≥10、y≥10,则x≤20,
故选:C.
8.解:由题意可设,
∵图象过点(20,1000),
∴k=20000.
∴.
∴当y=2000时,x=10.
观察图象可得:
∴当y≥2000时,0<x≤10.
故选:A.
9.解:当F一定时,P与S之间成反比例函数,则函数图象是双曲线,同时自变量是正数.
故选:A.
10.解:A、设反比例函数的解析式为y=,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=,
当x=4时,y=50,
∴4月份的利润为50万元,故此选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C、当y=100时,则100=,
解得:x=2,
则只有3月,4月,5月共3个月的利润低于100万元,故此选项不正确,符合题意.
D、设一次函数解析式为:y=kx+b,
则,
解得:,
故一次函数解析式为:y=30x﹣70,
故y=200时,200=30x﹣70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选:C.
11.解:如图所示,人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数关系是反比例函数,它的图象在第一象限,
∴y随x的增大而减小,
∴A,D错误,
设y=(k>0,x>0),把x=50时,y=1代入得:k=50,
∴y=,
把y=2代入上式得:x=25,
∴C错误,
把x=50代入上式得:y=1,
∴B正确,
故选:B.
12.解:由题意得,函数经过点(40,1),
把(40,1)代入t=,得k=40,
则解析式为t=,再把(m,0.5)代入t=,得m=80;
把v=60代入t=,得t=,
小时=40分钟,
则汽车通过该路段最少需要40分钟;
故选:B.
13.解:设A(x1,y1),B(x2,y2),代入y=中,得x1?y1=x2?y2=k,
联立,得x2﹣bx+k=0,
则x1?x2=k,又x1?y1=k,
∴x2=y1,
同理x2?y2=k,
可得x1=y2,
∴ON=OM,AM=BN,
∴①OA=OB,②△AOM≌△BON,正确;
③作OH⊥AB,垂足为H,
∵OA=OB,∠AOB=45°,
∵②△AOM≌△BON,正确;
∴∠MOA=∠BON=22.5°,
∠AOH=∠BOH=22.5°,
∴△OAM≌△OAH≌△OBH≌△OBN,
∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON=k+k=k,正确;
④延长MA,NB交于G点,
∵NG=OM=ON=MG,BN=AM,
∴GB=GA,
∴△ABG为等腰直角三角形,
当AB=时,GA=GB=1,
∴ON﹣BN=GN﹣BN=GB=1,正确.
正确的结论有4个.
故选:D.
14.解:过D点作DE⊥x轴,垂足为E,
由双曲线上点的性质,得S△AOC=S△DOE=k,
∵DE⊥x轴,AB⊥x轴,
∴DE∥AB,
∴△OAB∽△OED,
又∵OB=2OD,
∴S△OAB=4S△DOE=2k,
由S△OAB﹣S△OAC=S△OBC,
得2k﹣k=6,
解得k=4.
故选:D.
15.解:①点P是动点,
∴BP与AP不一定相等,
∴△BOP与△AOP不一定全等,故①不正确;
②设P(m,n),
∴BP∥y轴,
∴B(m,),
∴BP=|﹣n|,
∴S△BOP=×|﹣n|×|m|=|3﹣mn|,
∵PA∥x轴,
∴A(,n)
∴AP=|﹣m|,
∴SAOP=×|﹣m|×|n|=|3﹣mn|,
∴S△AOP=S△BOP,②正确;
③如图1,作PE⊥OB于E,PF⊥OA于F,
∵S△AOP=S△BOP,OA=OB,
∴PE=PF,
∵PE=PF,PE⊥OB,PF⊥OA,
∴OP平分∠AOB,③正确;
④如图2,延长BP交x轴于N,延长AP交y轴于M,
∴AM⊥y轴,BN⊥x轴,又∠MON=90°,
∴四边形OMPN是矩形,
∵点A,B在双曲线y=上,
∴S△AMO=S△BNO=3,
∵S△BOP=2,
∴S△PMO=S△PNO=1,
∴S矩形OMPN=2,
∴mn=2,
∴m=,
∴BP=|﹣n|=|3n﹣n|=2|n|,
AP=|﹣m|=||,
∴S△ABP=×2|n|×||=4,④错误;
故选:B.
16.解:∵矩形的面积为定值,长为8时,宽为5,
∴矩形的面积为40,
∴设长为y,宽为x,
则y=,
∴当长为10时,宽为:=4.
故答案为:4.
17.解:如图:
∵四边形ABCD、HBEO、OECF、GOFD为矩形,
又∵BO为四边形HBEO的对角线,OD为四边形OGDF的对角线,
∴S△BEO=S△BHO,S△OFD=S△OGD,S△CBD=S△ADB,
∴S△CBD﹣S△BEO﹣S△OFD=S△ADB﹣S△BHO﹣S△OGD,
∴S四边形HAGO=S四边形CEOF=2×2=4,
∴xy=k2+2k+1=4,
解得k=1或k=﹣3.
故答案为1或﹣3.
18.解:(1)药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,所以设y关于x的函数关系式是y=k1x(k≠0),
将点(8,6)代入,得:k1=,
即y=x,
自变量
x
的取值范围是0≤x≤8.
(2)设药物燃烧后y关于x的函数关系式是y=,把(8,6)代入得:
k=48,故y关于x的函数关系式是:y=;
故答案为:y=;
(3)当y=1.6时,代入y=得:x=30(分钟),
那么从消毒开始,至少需要经过30分钟后,学生才能回到教室.
19.解:(1)设当20≤x≤45时,反比例函数的解析式为y=,将C(20,45)代入得:
45=,解得k=900,
∴反比例函数的解析式为y=,
当x=45时,y==20,
∴D(45,20),
∴A(0,20),即A对应的指标值为20;
(2)设当0≤x<10时,AB的解析式为y=mx+n,将A(0,20)、B(10,45)代入得:
,解得,
∴AB的解析式为y=x+20,
当y≥36时,x+20≥36,解得x≥,
由(1)得反比例函数的解析式为y=,
当y≥36时,≥36,解得x≤25,
∴≤x≤25时,注意力指标都不低于36,
而25﹣=>17,
∴张老师能经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36.
20.解:(1)设v与t的函数关系式为v=,
将(5,120)代入v=,得:120=,
解得:k=600,
∴v与t的函数关系式为v=(5≤t≤10);
(2)①当t=(8时到14时40分)时,v==600÷=90(千米/时),
当t=时,v==600÷=80(千米/时),
∴客车行驶速度v的范围为80千米/时≤v≤90千米/时;
②当天12时30分到达时,t=4.5<5,
而5≤t≤10,
故客车不能在当天12时30分前到达乙地.
一、选择题
1.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A.
B.
C.
D.
2.如图过y轴一个动点M作x轴的平行线,交双曲线于点A,交双曲线于点B,点C、点D在x轴上运动,且始终保持DC=AB,则平行四边形ABCD的面积是( )
A.7
B.10
C.14
D.28
3.下列两个变量之间的关系为反比例关系的是( )
A.圆的周长与其半径的关系
B.平行四边形面积一定时,其一边长与这边上的高的关系
C.销售单价一定时,销售总价与销售数量的关系
D.汽车匀速行驶过程中,行驶路程与行驶时间的关系
4.为预防新冠病毒,某学校每周末用药熏消毒法对教室进行消毒,已知药物释放过程中,教室内每立方米空气中含药量y(mg)与时间t(h)成正比例;药物释放完毕后,y与t成反比例,如图所示.根据图象信息,下列选项错误的是( )
A.药物释放过程需要小时
B.药物释放过程中,y与t的函数表达式是y=t
C.空气中含药量大于等于0.5mg/m3的时间为h
D.若当空气中含药量降低到0.25mg/m3以下时对身体无害,那么从消毒开始,至少需要经过4.5小时学生才能进入教室
5.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A.不小于0.5m3
B.不大于0.5m3
C.不小于0.6m3
D.不大于0.6m3
6.某校对学生宿舍采取喷洒药物进行消毒,在对某宿舍进行消毒的过程中,先经过5min的集中药物喷洒,再封闭宿舍10min,然后打开门窗进行通风,室内每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(min)之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
A.经过5min集中喷洒药物,室内空气中的含药量最高达到10mg/m3
B.室内空气中的含药量不低于8mg/m3的持续时间达到了11min
C.此次消毒完全有效.(有效的标准为:当室内空气中的含药量不低于5mg/m3,且持续时间不低于35分钟)
D.当室内空气中的含药量低于2mg/m3时,对人体才是安全的,所以从室内空气中的含药量达到2mg/m3开始,需经过59min后,学生才能进入室内
7.某学校要种植一块面积为200m2的长方形草坪,要求两边长均不小于10m,则草坪的一边长y(单位:m)随另一边长x(单位:m)的变化而变化的图象可能是( )
A.B.C.D.
8.已知某品牌显示器的使用寿命为定值.这种显示器可工作的天数y与平均每天工作的小时数x是反比例函数关系,图象如图所示.如果这种显示器至少要用2000天,那么显示器平均每天工作的小时数x应控制在( )
A.0<x≤10
B.10≤x≤24
C.0<x≤20
D.20≤x≤24
9.当压力F(N)一定时,物体所受的压强P(Pa)与受力面积S(m2)的函数关系式为P=(S≠0),这个函数的图象大致是( )
A.
B.
C.
D.
10.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
11.某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口有100人
D.该村人均耕地面积y与总人口x成正比例
12.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5),若行驶速度不得超过60(km/h),则汽车通过该路段最少需要时间为( )
A.分
B.40分
C.60分
D.分
13.如图,直线y=﹣x+b(b>0)与双曲线y=(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N;有以下结论:
①OA=OB
②△AOM≌△BON
③若∠AOB=45°,则S△AOB=k
④当AB=时,ON﹣BN=1;
其中结论正确的个数为( )
A.1
B.2
C.3
D.4
14.如图,已知双曲线经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为6,则k的值为( )
A.1
B.2
C.3
D.4
15.如图,A、B是函数y=(x>0)上两点,点P在第一象限,且在函数y=(x>0)下方,作PB⊥x轴,PA⊥y轴,下列说法正确的是( )
①△AOP≌△BOP;
②S△AOP=S△BOP;
③若OA=OB,则OP平分∠AOB;
④若S△BOP=2,则S△ABP=6.
A.1个
B.2个
C.3个
D.4个
二、填空题
16.面积一定的长方形,长为8时宽为5,当长为10时,宽为
.
17.如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数的图象上.若点A的坐标为(﹣2,﹣2),则k的值为
.
三、解答题
18.为了预防“流感”,某学校对教室采取药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y与x成反比例(如图所示).现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克.
(1)求药物燃烧时y关于x的函数关系式及其自变量x的取值范围;
(2)药物燃烧后y关于x的函数关系式是
;
(3)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回到教室.
19.通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当0≤x<10和10≤x<20时,图象是线段;当20≤x≤45时,图象是反比例函数的一部分.
(1)求点A对应的指标值;
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.
20.一辆客车从甲地出发前往乙地,平均速度v(千米/时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)求v与t的函数关系式及t值的取值范围;
(2)客车上午8时从甲地出发.
①客车需在当天14时40分至15时30分(含14时40分与15时30分)间到达乙地,求客车行驶速度v的范围;
②客车能否在当天12时30分前到达乙地?说明理由.
参考答案
1.解:设用电阻R表示电流I的函数解析式为I=,
∵过(2,3),
∴k=3×2=6,
∴I=,
故选:D.
2.解:设M的坐标为(0,m)(m>0),则直线AB的方程为:y=m,
将y=m代入y=﹣中得:x=﹣,∴A(﹣,m),
将y=m代入y=中得:x=,∴B(,m),
∴DC=AB=﹣(﹣)=,
过B作BN⊥x轴,则有BN=m,
则平行四边形ABCD的面积S=DC?BN=?m=14.故选:C.
3.解:A.圆的周长与其半径是正比例函数,故不符合题意;
B.平行四边形面积一定时,其一边长与这边上的高是反比例函数,故符合题意;
C.销售单价一定时,销售总价与销售数量是正比例函数,故不符合题意;
D.汽车匀速行驶过程中,行驶路程与行驶时间是正比例函数,故不符合题意.
故选:B.
4.解:设正比例函数解析式是y=kt,
反比例函数解析式是y=,
把点(3,)分别代入反比例函数解析式得:=,
解得:m=,
∴反比例函数解析式是y=,
当y=1时,代入上式得t=,
把t=时,y=1代入正比例函数解析式是y=kt得:k=,
∴正比例函数解析式是y=t,
A.由图象知,y=1时,t=,即药物释放过程需要小时,故A不符合题意;
B.药物释放过程中,y与t的成正比例,函数表达式是y=t,故B不符合题意;
C.把y=0.5mg/m3分别代入y=t和y=得,0.5=t1和0.5=,
解得:t1=和t2=3,
∴t2﹣t1=,
∴空气中含药量大于等于0.5mg/m3的时间为h;故C不符合题意;
<0.25,
解得t>6,
所以至少需要经过6小时后,学生才能进入教室,故D符合题意,
故选:D.
5.解:设函数解析式为P=,
∵当V=1.5m3时,p=16000Pa,
∴k=Vp=24000,
∴p=,
∵气球内的气压大于40000Pa时,气球将爆炸,
∴≤40000,
解得:V≥0.6,即气球的体积应不小于0.6m3.
故选:C.
6.解:A、由图象可得此选项正确,不符合题意.
B、由题意x=4时,y=8,故室内空气中的含药量不低于8mg/m3的持续时间达到了11min,正确,不符合题意;
C、y=5时,x=2.5或24,24﹣2.5=21.5<35,故本选项错误,符合题意;
D、当x≤5时,函数关系式为y=2x,y=2时,x=1;当x>15时,函数关系式为y=,y=2时,x=60;60﹣1=59,故当室内空气中的含药量低于2mg/m3时,对人体才是安全的,所以从室内空气中的含药量达到2mg/m3开始,需经过59min后,学生才能进入室内,正确.不符合题意,
故选:C.
7.解:∵草坪面积为200m2,
∴x、y存在关系y=,
∵两边长均不小于10m,
∴x≥10、y≥10,则x≤20,
故选:C.
8.解:由题意可设,
∵图象过点(20,1000),
∴k=20000.
∴.
∴当y=2000时,x=10.
观察图象可得:
∴当y≥2000时,0<x≤10.
故选:A.
9.解:当F一定时,P与S之间成反比例函数,则函数图象是双曲线,同时自变量是正数.
故选:A.
10.解:A、设反比例函数的解析式为y=,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=,
当x=4时,y=50,
∴4月份的利润为50万元,故此选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C、当y=100时,则100=,
解得:x=2,
则只有3月,4月,5月共3个月的利润低于100万元,故此选项不正确,符合题意.
D、设一次函数解析式为:y=kx+b,
则,
解得:,
故一次函数解析式为:y=30x﹣70,
故y=200时,200=30x﹣70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选:C.
11.解:如图所示,人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数关系是反比例函数,它的图象在第一象限,
∴y随x的增大而减小,
∴A,D错误,
设y=(k>0,x>0),把x=50时,y=1代入得:k=50,
∴y=,
把y=2代入上式得:x=25,
∴C错误,
把x=50代入上式得:y=1,
∴B正确,
故选:B.
12.解:由题意得,函数经过点(40,1),
把(40,1)代入t=,得k=40,
则解析式为t=,再把(m,0.5)代入t=,得m=80;
把v=60代入t=,得t=,
小时=40分钟,
则汽车通过该路段最少需要40分钟;
故选:B.
13.解:设A(x1,y1),B(x2,y2),代入y=中,得x1?y1=x2?y2=k,
联立,得x2﹣bx+k=0,
则x1?x2=k,又x1?y1=k,
∴x2=y1,
同理x2?y2=k,
可得x1=y2,
∴ON=OM,AM=BN,
∴①OA=OB,②△AOM≌△BON,正确;
③作OH⊥AB,垂足为H,
∵OA=OB,∠AOB=45°,
∵②△AOM≌△BON,正确;
∴∠MOA=∠BON=22.5°,
∠AOH=∠BOH=22.5°,
∴△OAM≌△OAH≌△OBH≌△OBN,
∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON=k+k=k,正确;
④延长MA,NB交于G点,
∵NG=OM=ON=MG,BN=AM,
∴GB=GA,
∴△ABG为等腰直角三角形,
当AB=时,GA=GB=1,
∴ON﹣BN=GN﹣BN=GB=1,正确.
正确的结论有4个.
故选:D.
14.解:过D点作DE⊥x轴,垂足为E,
由双曲线上点的性质,得S△AOC=S△DOE=k,
∵DE⊥x轴,AB⊥x轴,
∴DE∥AB,
∴△OAB∽△OED,
又∵OB=2OD,
∴S△OAB=4S△DOE=2k,
由S△OAB﹣S△OAC=S△OBC,
得2k﹣k=6,
解得k=4.
故选:D.
15.解:①点P是动点,
∴BP与AP不一定相等,
∴△BOP与△AOP不一定全等,故①不正确;
②设P(m,n),
∴BP∥y轴,
∴B(m,),
∴BP=|﹣n|,
∴S△BOP=×|﹣n|×|m|=|3﹣mn|,
∵PA∥x轴,
∴A(,n)
∴AP=|﹣m|,
∴SAOP=×|﹣m|×|n|=|3﹣mn|,
∴S△AOP=S△BOP,②正确;
③如图1,作PE⊥OB于E,PF⊥OA于F,
∵S△AOP=S△BOP,OA=OB,
∴PE=PF,
∵PE=PF,PE⊥OB,PF⊥OA,
∴OP平分∠AOB,③正确;
④如图2,延长BP交x轴于N,延长AP交y轴于M,
∴AM⊥y轴,BN⊥x轴,又∠MON=90°,
∴四边形OMPN是矩形,
∵点A,B在双曲线y=上,
∴S△AMO=S△BNO=3,
∵S△BOP=2,
∴S△PMO=S△PNO=1,
∴S矩形OMPN=2,
∴mn=2,
∴m=,
∴BP=|﹣n|=|3n﹣n|=2|n|,
AP=|﹣m|=||,
∴S△ABP=×2|n|×||=4,④错误;
故选:B.
16.解:∵矩形的面积为定值,长为8时,宽为5,
∴矩形的面积为40,
∴设长为y,宽为x,
则y=,
∴当长为10时,宽为:=4.
故答案为:4.
17.解:如图:
∵四边形ABCD、HBEO、OECF、GOFD为矩形,
又∵BO为四边形HBEO的对角线,OD为四边形OGDF的对角线,
∴S△BEO=S△BHO,S△OFD=S△OGD,S△CBD=S△ADB,
∴S△CBD﹣S△BEO﹣S△OFD=S△ADB﹣S△BHO﹣S△OGD,
∴S四边形HAGO=S四边形CEOF=2×2=4,
∴xy=k2+2k+1=4,
解得k=1或k=﹣3.
故答案为1或﹣3.
18.解:(1)药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,所以设y关于x的函数关系式是y=k1x(k≠0),
将点(8,6)代入,得:k1=,
即y=x,
自变量
x
的取值范围是0≤x≤8.
(2)设药物燃烧后y关于x的函数关系式是y=,把(8,6)代入得:
k=48,故y关于x的函数关系式是:y=;
故答案为:y=;
(3)当y=1.6时,代入y=得:x=30(分钟),
那么从消毒开始,至少需要经过30分钟后,学生才能回到教室.
19.解:(1)设当20≤x≤45时,反比例函数的解析式为y=,将C(20,45)代入得:
45=,解得k=900,
∴反比例函数的解析式为y=,
当x=45时,y==20,
∴D(45,20),
∴A(0,20),即A对应的指标值为20;
(2)设当0≤x<10时,AB的解析式为y=mx+n,将A(0,20)、B(10,45)代入得:
,解得,
∴AB的解析式为y=x+20,
当y≥36时,x+20≥36,解得x≥,
由(1)得反比例函数的解析式为y=,
当y≥36时,≥36,解得x≤25,
∴≤x≤25时,注意力指标都不低于36,
而25﹣=>17,
∴张老师能经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36.
20.解:(1)设v与t的函数关系式为v=,
将(5,120)代入v=,得:120=,
解得:k=600,
∴v与t的函数关系式为v=(5≤t≤10);
(2)①当t=(8时到14时40分)时,v==600÷=90(千米/时),
当t=时,v==600÷=80(千米/时),
∴客车行驶速度v的范围为80千米/时≤v≤90千米/时;
②当天12时30分到达时,t=4.5<5,
而5≤t≤10,
故客车不能在当天12时30分前到达乙地.
