2021-2022学年鲁教版(五四制)九年级数学上册2.6利用三角函数测高优生辅导专题提升训练(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学上册2.6利用三角函数测高优生辅导专题提升训练(Word版,附答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 343.9KB | ||
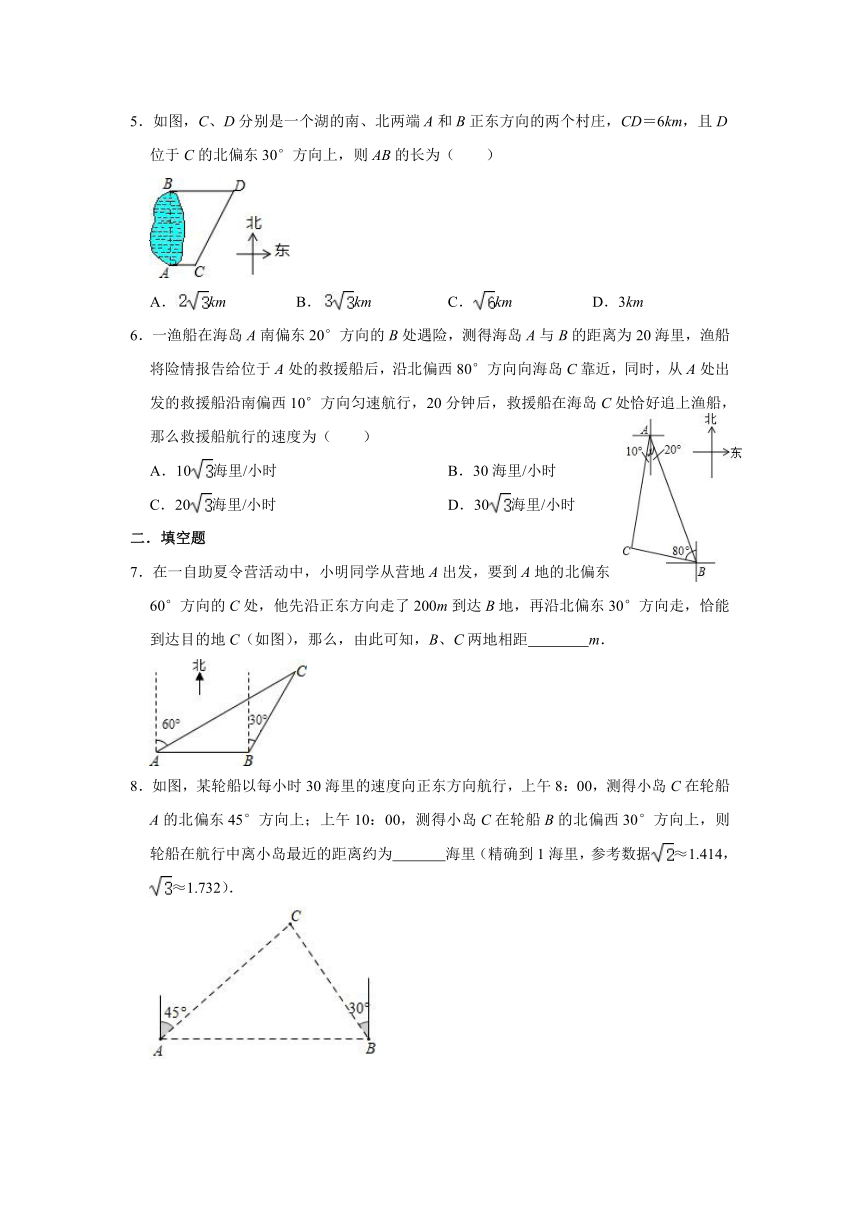
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 23:28:03 | ||
图片预览



文档简介
2021年鲁教版九年级数学上册《2.6利用三角函数测高》优生辅导专题提升训练(附答案)
一.选择题
1.如图,为了测量河两岸A、B两点的距离,在与AB垂直的方向点C处测得AC=a,∠ACB=α,那么AB等于( )
A.a?sinα
B.a?tanα
C.a?cosα
D.
2.如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔2海里的点A处.若海轮沿正南方向航行到灯塔的正东位置B处,则海轮航行的距离AB的长是( )
A.2sin50°海里
B.2cos50°海里
C.2tan40°海里
D.2tan50°海里
3.一艘轮船由海平面上A地出发向南偏西30°的方向行驶50海里到达B地,再由B地向北偏西30°的方向行驶50海里到达C地,则A、C两地相距( )
A.100海里
B.50海里
C.50海里
D.25海里
4.如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
A.10海里
B.10海里
C.10海里
D.20海里
5.如图,C、D分别是一个湖的南、北两端A和B正东方向的两个村庄,CD=6km,且D位于C的北偏东30°方向上,则AB的长为( )
A.km
B.km
C.km
D.3km
6.一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为( )
A.10海里/小时
B.30海里/小时
C.20海里/小时
D.30海里/小时
二.填空题
7.在一自助夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距
m.
8.如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为
海里(精确到1海里,参考数据≈1.414,≈1.732).
9.如图,码头A在码头B的正东方向,两个码头之间的距离为10海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,则码头A与小岛C的距离为
海里(结果保留根号).
10.一船向东航行,上午9时,在灯塔的西南20海里的B处,上午11时到达这灯塔的正南方向C处,则这船航行的速度是
海里/小时.
11.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔20海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的北偏东60°方向上的B处,则此时轮船与灯塔的距离BP为
海里.
三.解答题
12.如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.
(1)求∠CBA的度数.
(2)求出这段河的宽(结果精确到1m,备用数据≈1.41,≈1.73).
13.如图,一艘轮船在海上以每小时36海里的速度向正西方向航行,上午8时,在B处测得小岛A在北偏东30°方向,之后轮船继续向正西方向航行,于上午9时到达C处,这时测得小岛A在北偏东60°方向.如果轮船仍继续向正西方向航行,于上午11时到达D处,这时轮船与小岛A相距多远?
14.如图,设计一个“奔跑”游戏:路线需经A、B、C、D四地.A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向,且BC=CD=2km.
(1)证明路程AB+BD+DC与AB+BC+CD相等;
(2)从A地跑到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,≈1.4)
15.如图,在港口A处的正西方向有两个观测点B,C.一艘轮船从A处出发,沿北偏西26°方向航行60km至D处,在B,C处分别测得∠DBA=45°,∠C=37°.求两个观察点B,C相距的距离.(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)
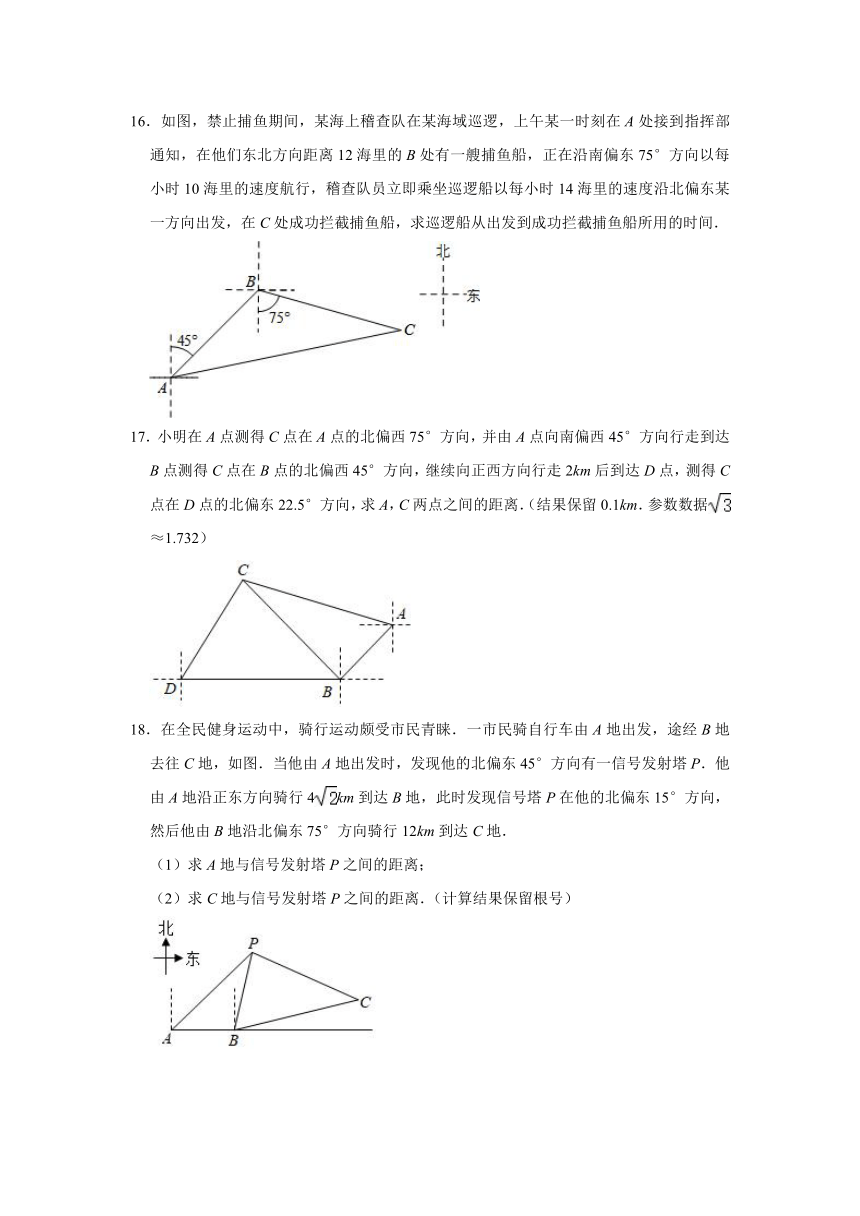
16.如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
17.小明在A点测得C点在A点的北偏西75°方向,并由A点向南偏西45°方向行走到达B点测得C点在B点的北偏西45°方向,继续向正西方向行走2km后到达D点,测得C点在D点的北偏东22.5°方向,求A,C两点之间的距离.(结果保留0.1km.参数数据≈1.732)
18.在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东45°方向有一信号发射塔P.他由A地沿正东方向骑行4km到达B地,此时发现信号塔P在他的北偏东15°方向,然后他由B地沿北偏东75°方向骑行12km到达C地.
(1)求A地与信号发射塔P之间的距离;
(2)求C地与信号发射塔P之间的距离.(计算结果保留根号)
19.时代中学组织学生进行红色研学活动.学生到达爱国主义教育基地后,先从基地门口A处向正南方向走300米到达革命纪念碑B处,再从B处向正东方向走到党史纪念馆C处,然后从C处向北偏西37°方向走200米到达人民英雄雕塑D处,最后从D处回到A处.已知人民英雄雕塑在基地门口的南偏东65°方向,求革命纪念碑与党史纪念馆之间的距离(精确到1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
20.海上测绘船沿正北方向航行,在A点观察东西方向的岛屿的西端M在A点的北偏东36.9°方向航行4km后到达B点,测得该岛屿东端N在B点的北偏东67.4°方向,又航行6km后到达C点,测得该岛屿正好在C点的正东方向(即C,M,N在同一直线上)求该岛屿东西两端M,N之间的距离.(参考数据:sin36.9°≈0.60,tan36.9°≈0.75,sin67.4°≈0.92,tan67.4°≈2.40)
参考答案
一.选择题
1.解:根据题意,在Rt△ABC,有AC=a,∠ACB=α,且tanα=,
则AB=AC×tanα=a?tanα,
故选:B.
2.解:由题意可知∠NPA=50°,PA=6海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=50°.
在Rt△ABP中,∵∠ABP=90°,∠A=50°,PA=2海里,
∴AB=AP?cos∠A=2cos50°海里.
故选:B.
3.解:∵由海平面上A地出发向南偏西30°的方向行驶50海里到达B地,再由B地向北偏西30°的方向行驶50海里到达C地,
∴∠ABC=60°,AB=BC=50海里,
∴△ABC是等边三角形,
∴AC=AB=50海里,
故选:C.
4.解:作BD⊥AC于点D.
∵∠CBA=25°+50°=75°,
∴∠CAB=(90°﹣70°)+(90°﹣50°)=20°+40°=60°,
∠ABD=30°,
∴∠CBD=75°﹣30°=45°.
在直角△ABD中,BD=AB?sin∠CAB=20×sin60°=20×=10.
在直角△BCD中,∠CBD=45°,
则BC=BD=10×=10(海里).
故选:C.
5.解:过C作CE⊥BD于E,则CE=AB.
直角△CED中,∠ECD=30°,CD=6,
则CE=CD?cos30°=3=AB.
所以AB=3(km).
故选:B.
6.解:∵∠CAB=10°+20°=30°,∠CBA=80°﹣20°=60°,
∴∠C=90°,
∵AB=20海里,
∴AC=AB?cos30°=10(海里),
∴救援船航行的速度为:10÷=30(海里/小时).
故选:D.
二.填空题
7.解:由已知得:
∠ABC=90°+30°=120°,
∠BAC=90°﹣60°=30°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=180°﹣120°﹣30°=30°,
∴∠ACB=∠BAC,
∴BC=AB=200.
故答案为:200.
8.解:根据题意可知:
AB=30×(10﹣8)=60(海里),∠ACD=45°,∠BCD=30°,
如图,作CD⊥AB于点D,
在Rt△ACD中,CD=AD,
在Rt△CBD中,BD=AB﹣AD=60﹣CD,
∴tan30°=,
即=,
解得CD≈38(海里).
答:轮船在航行中离小岛最近的距离约为38海里.
故答案为:38.
9.解:作CD⊥AB交AB延长线于点D,
由题意,得∠DCB=45°,∠CAD=90°﹣60°=30°,AB=10海里,
设CD=x海里,
在Rt△DCB中,tan∠DCB=,tan45°==1,
∴BD=x,
则AD=AB+BD=10+x,
由tan30°=,
解得x=5+5,
∵∠CAD=30°,∠CDA=90°,
∴AC=2CD=(10+10)海里.
故答案为:(10+10).
10.解:∵AB=20,∠BAC=45°,
∴AC=BC=10.
∵从B到C用时11﹣9=2时,
∴速度为10÷2=5(海里/小时).
11.解:如图,由题意,可知PA=20海里,∠1=30°,∠1+∠APB=60°,则∠APB=30°,∠2=30°.
∵PQ∥AB,
∴∠B=∠2=30°,
∴PA=AB=20海里,
过点A作AC⊥PB于点C,则BP=2PC.
在Rt△PAC中,∵PA=20海里,∠APC=30°,
∴PC=AP?cos∠APC=20×=10海里.
∴BP=2PC=20海里.
即此时轮船与灯塔的距离BP为20海里.
故答案为20.
三.解答题
12.解:(1)由题意得,∠BAD=45°,∠BCA=30°,
∴∠CBA=∠BAD﹣∠BCA=15°;
(2)作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CD==x,
∵∠BAD=45°,
∴AD=BD=x,
则x﹣x=60,
解得x=≈82,
答:这段河的宽约为82m.
13.解:作AE⊥BD于点E,
则∠ACB=90°﹣60°=30°,∠ABE=90°﹣30°=60°,
∵∠ABE=∠ACB+∠CAB
∴∠CAB=30°
∴∠ACB=∠CAB
∴AB=BC=36海里,
在直角△ABE中,∠ABE=60°,
∴AE=AB=18海里,BE=AB=18海里,
在直角△ADE中,DE=126海里,
根据勾股定理得到AD===36海里.
14.(1)证明:根据两直线平行,同旁内角互补可得,∠DCA+45°+75°=180°,
∴∠DCA=180°﹣75°﹣45°=60°,
∵BC=CD,
∴△BCD是等边三角形.
∴BC=BD,
∴AB+BD+DC=AB+BC+CD;
(2)解:过点B作BE垂直于AD,垂足为E,
由题意可知∠DAC=75°﹣30°=45°,
∵△BCD是等边三角形,
∴∠DBC=60°,BD=BC=CD=2km,
∵∠DBC=∠DAC+∠ADB
∴∠ADB=∠DBC﹣∠DAC=15°,
在Rt△BDE中,sin∠ADB=,
∴BE=BD?sin15°≈2×0.26≈0.52(km),
在Rt△ABE中,sin∠EAB=,
∴AB==0.52×≈0.52×1.4≈0.7(km),
∴AB+BC+CD≈0.7+2+2≈4.7(km).
答:从A地跑到D地的路程大约是4.7km.
15.解:过点D作DE⊥AC,垂足为E,如图所示:
在Rt△ABE中,AD=60km,∠ADE=26°,
∴DE=AD?cos∠ADE=60×cos26°≈60×0.9=54(km),
∵∠DBE=45°,∠DEB=90°,
∴BE=DE=54km,
∵∠C=37°,
∴,
∴CE=.
∴CE≈54÷0.75=72(km),
∴BC=CE﹣BE=72﹣54=18(km),
答:两个观察点B,C相距的距离为18海里.
16.解:设巡逻船从出发到成功拦截所用时间为x小时;如图所示,
由题意得:∠ABC=45°+75°=120°,AB=12,BC=10x,AC=14x,
过点A作AD⊥CB的延长线于点D,
在Rt△ABD中,AB=12,∠ABD=45°+(90°﹣75°)=60°,
∴BD=AB?cos60°=AB=6,AD=AB?sin60°=6,
∴CD=10x+6.
在Rt△ACD中,由勾股定理得:,
解得:(不合题意舍去).
答:巡逻船从出发到成功拦截所用时间为2小时.
17.解:过点A作AM∥BD,过B点作BM⊥BD,AM与BM交于点M,
∵在A点测得C点在A点的北偏西75°方向,
∴∠NAC=75°,
∴∠CAM=15°,
∵由A点向南偏西45°方向行走到达B点,
∴∠MAB=45°,
∴∠MBA=45°,
∵C点在B点的北偏西45°方向,
∴∠CBM=45°,
∴∠CBA=90°,∠CBD=45°,
∵C点在D点的北偏东22.5°方向,
∴∠PDC=22.5°,
∴∠DCB=67.5°,
∴∠BDC=180°﹣67.5°﹣45°=67.5°,
∴BD=BC,
由题可得DB=2km,
∴BC=2km,
在Rt△ABC中,∠CAB=15°+45°=60°,BC=2,
∴AC=≈1.3km.
18.解:(1)依题意知:∠PAB=45°,∠PBG=15°,∠GBC=75°,
过点B作BD⊥AP于D点,
∵∠DAB=45°,,
∴AD=BD=4,
∵∠ABD=∠GBD=45°,∠GBP=15°,
∴∠PBD=60°,
∵BD=4,
∴,
∴PA=(4+4)(km);
(2)∵∠PBD=60°,BD=4,
∴PB=8,
过点P作PE⊥BC于E,
∵∠PBG=15°,∠GBC=75°,
∴∠PBE=60°,
∵PB=8,
∴BE=4,,
∵BC=12,
∴CE=8,
∴PC=4(km).
19.解:过D作DE⊥AB于E,DF⊥BC于F,如图所示:
由题意得:∠CDF=37°,CD=200米,
在Rt△CDF中,sin∠CDF==sin37°≈0.60,cos∠CDF==cos37°≈0.80,
∴CF≈200×0.60=120(米),DF≈200×0.80=160(米),
∵AB⊥BC,DF⊥BC,DE⊥AB,
∴∠B=∠DFB=∠DEB=90°,
∴四边形BFDE是矩形,
∴BF=DE,BE=DF=160米,
∴AE=AB﹣BE=300﹣160=140(米),
在Rt△ADE中,tan∠DAE==tan65°≈2.14,
∴DE≈AE×2.14=140×2.14=299.60(米),
∴BF=DE≈299.60(米),
∴BC=BF+CF=299.60+120≈420(米),
答:革命纪念碑与党史纪念馆之间的距离约为420米.
20.解:AC=AB+BC=4+6=10(km),
在Rt△ACM中,tan∠CAM==tan36.9°≈0.75,
∴CM≈7.5(km),
在Rt△BCN中,tan∠CBN==tan67.4°≈2.40,
∴CN≈14.4(km),
∴MN=CN﹣CM≈14.4﹣7.5=6.9(km).
答:该岛屿东西两端M,N之间的距离约为6.9km.
一.选择题
1.如图,为了测量河两岸A、B两点的距离,在与AB垂直的方向点C处测得AC=a,∠ACB=α,那么AB等于( )
A.a?sinα
B.a?tanα
C.a?cosα
D.
2.如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔2海里的点A处.若海轮沿正南方向航行到灯塔的正东位置B处,则海轮航行的距离AB的长是( )
A.2sin50°海里
B.2cos50°海里
C.2tan40°海里
D.2tan50°海里
3.一艘轮船由海平面上A地出发向南偏西30°的方向行驶50海里到达B地,再由B地向北偏西30°的方向行驶50海里到达C地,则A、C两地相距( )
A.100海里
B.50海里
C.50海里
D.25海里
4.如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
A.10海里
B.10海里
C.10海里
D.20海里
5.如图,C、D分别是一个湖的南、北两端A和B正东方向的两个村庄,CD=6km,且D位于C的北偏东30°方向上,则AB的长为( )
A.km
B.km
C.km
D.3km
6.一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为( )
A.10海里/小时
B.30海里/小时
C.20海里/小时
D.30海里/小时
二.填空题
7.在一自助夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距
m.
8.如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为
海里(精确到1海里,参考数据≈1.414,≈1.732).
9.如图,码头A在码头B的正东方向,两个码头之间的距离为10海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,则码头A与小岛C的距离为
海里(结果保留根号).
10.一船向东航行,上午9时,在灯塔的西南20海里的B处,上午11时到达这灯塔的正南方向C处,则这船航行的速度是
海里/小时.
11.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔20海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的北偏东60°方向上的B处,则此时轮船与灯塔的距离BP为
海里.
三.解答题
12.如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.
(1)求∠CBA的度数.
(2)求出这段河的宽(结果精确到1m,备用数据≈1.41,≈1.73).
13.如图,一艘轮船在海上以每小时36海里的速度向正西方向航行,上午8时,在B处测得小岛A在北偏东30°方向,之后轮船继续向正西方向航行,于上午9时到达C处,这时测得小岛A在北偏东60°方向.如果轮船仍继续向正西方向航行,于上午11时到达D处,这时轮船与小岛A相距多远?
14.如图,设计一个“奔跑”游戏:路线需经A、B、C、D四地.A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向,且BC=CD=2km.
(1)证明路程AB+BD+DC与AB+BC+CD相等;
(2)从A地跑到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,≈1.4)
15.如图,在港口A处的正西方向有两个观测点B,C.一艘轮船从A处出发,沿北偏西26°方向航行60km至D处,在B,C处分别测得∠DBA=45°,∠C=37°.求两个观察点B,C相距的距离.(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)
16.如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
17.小明在A点测得C点在A点的北偏西75°方向,并由A点向南偏西45°方向行走到达B点测得C点在B点的北偏西45°方向,继续向正西方向行走2km后到达D点,测得C点在D点的北偏东22.5°方向,求A,C两点之间的距离.(结果保留0.1km.参数数据≈1.732)
18.在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东45°方向有一信号发射塔P.他由A地沿正东方向骑行4km到达B地,此时发现信号塔P在他的北偏东15°方向,然后他由B地沿北偏东75°方向骑行12km到达C地.
(1)求A地与信号发射塔P之间的距离;
(2)求C地与信号发射塔P之间的距离.(计算结果保留根号)
19.时代中学组织学生进行红色研学活动.学生到达爱国主义教育基地后,先从基地门口A处向正南方向走300米到达革命纪念碑B处,再从B处向正东方向走到党史纪念馆C处,然后从C处向北偏西37°方向走200米到达人民英雄雕塑D处,最后从D处回到A处.已知人民英雄雕塑在基地门口的南偏东65°方向,求革命纪念碑与党史纪念馆之间的距离(精确到1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
20.海上测绘船沿正北方向航行,在A点观察东西方向的岛屿的西端M在A点的北偏东36.9°方向航行4km后到达B点,测得该岛屿东端N在B点的北偏东67.4°方向,又航行6km后到达C点,测得该岛屿正好在C点的正东方向(即C,M,N在同一直线上)求该岛屿东西两端M,N之间的距离.(参考数据:sin36.9°≈0.60,tan36.9°≈0.75,sin67.4°≈0.92,tan67.4°≈2.40)
参考答案
一.选择题
1.解:根据题意,在Rt△ABC,有AC=a,∠ACB=α,且tanα=,
则AB=AC×tanα=a?tanα,
故选:B.
2.解:由题意可知∠NPA=50°,PA=6海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=50°.
在Rt△ABP中,∵∠ABP=90°,∠A=50°,PA=2海里,
∴AB=AP?cos∠A=2cos50°海里.
故选:B.
3.解:∵由海平面上A地出发向南偏西30°的方向行驶50海里到达B地,再由B地向北偏西30°的方向行驶50海里到达C地,
∴∠ABC=60°,AB=BC=50海里,
∴△ABC是等边三角形,
∴AC=AB=50海里,
故选:C.
4.解:作BD⊥AC于点D.
∵∠CBA=25°+50°=75°,
∴∠CAB=(90°﹣70°)+(90°﹣50°)=20°+40°=60°,
∠ABD=30°,
∴∠CBD=75°﹣30°=45°.
在直角△ABD中,BD=AB?sin∠CAB=20×sin60°=20×=10.
在直角△BCD中,∠CBD=45°,
则BC=BD=10×=10(海里).
故选:C.
5.解:过C作CE⊥BD于E,则CE=AB.
直角△CED中,∠ECD=30°,CD=6,
则CE=CD?cos30°=3=AB.
所以AB=3(km).
故选:B.
6.解:∵∠CAB=10°+20°=30°,∠CBA=80°﹣20°=60°,
∴∠C=90°,
∵AB=20海里,
∴AC=AB?cos30°=10(海里),
∴救援船航行的速度为:10÷=30(海里/小时).
故选:D.
二.填空题
7.解:由已知得:
∠ABC=90°+30°=120°,
∠BAC=90°﹣60°=30°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=180°﹣120°﹣30°=30°,
∴∠ACB=∠BAC,
∴BC=AB=200.
故答案为:200.
8.解:根据题意可知:
AB=30×(10﹣8)=60(海里),∠ACD=45°,∠BCD=30°,
如图,作CD⊥AB于点D,
在Rt△ACD中,CD=AD,
在Rt△CBD中,BD=AB﹣AD=60﹣CD,
∴tan30°=,
即=,
解得CD≈38(海里).
答:轮船在航行中离小岛最近的距离约为38海里.
故答案为:38.
9.解:作CD⊥AB交AB延长线于点D,
由题意,得∠DCB=45°,∠CAD=90°﹣60°=30°,AB=10海里,
设CD=x海里,
在Rt△DCB中,tan∠DCB=,tan45°==1,
∴BD=x,
则AD=AB+BD=10+x,
由tan30°=,
解得x=5+5,
∵∠CAD=30°,∠CDA=90°,
∴AC=2CD=(10+10)海里.
故答案为:(10+10).
10.解:∵AB=20,∠BAC=45°,
∴AC=BC=10.
∵从B到C用时11﹣9=2时,
∴速度为10÷2=5(海里/小时).
11.解:如图,由题意,可知PA=20海里,∠1=30°,∠1+∠APB=60°,则∠APB=30°,∠2=30°.
∵PQ∥AB,
∴∠B=∠2=30°,
∴PA=AB=20海里,
过点A作AC⊥PB于点C,则BP=2PC.
在Rt△PAC中,∵PA=20海里,∠APC=30°,
∴PC=AP?cos∠APC=20×=10海里.
∴BP=2PC=20海里.
即此时轮船与灯塔的距离BP为20海里.
故答案为20.
三.解答题
12.解:(1)由题意得,∠BAD=45°,∠BCA=30°,
∴∠CBA=∠BAD﹣∠BCA=15°;
(2)作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CD==x,
∵∠BAD=45°,
∴AD=BD=x,
则x﹣x=60,
解得x=≈82,
答:这段河的宽约为82m.
13.解:作AE⊥BD于点E,
则∠ACB=90°﹣60°=30°,∠ABE=90°﹣30°=60°,
∵∠ABE=∠ACB+∠CAB
∴∠CAB=30°
∴∠ACB=∠CAB
∴AB=BC=36海里,
在直角△ABE中,∠ABE=60°,
∴AE=AB=18海里,BE=AB=18海里,
在直角△ADE中,DE=126海里,
根据勾股定理得到AD===36海里.
14.(1)证明:根据两直线平行,同旁内角互补可得,∠DCA+45°+75°=180°,
∴∠DCA=180°﹣75°﹣45°=60°,
∵BC=CD,
∴△BCD是等边三角形.
∴BC=BD,
∴AB+BD+DC=AB+BC+CD;
(2)解:过点B作BE垂直于AD,垂足为E,
由题意可知∠DAC=75°﹣30°=45°,
∵△BCD是等边三角形,
∴∠DBC=60°,BD=BC=CD=2km,
∵∠DBC=∠DAC+∠ADB
∴∠ADB=∠DBC﹣∠DAC=15°,
在Rt△BDE中,sin∠ADB=,
∴BE=BD?sin15°≈2×0.26≈0.52(km),
在Rt△ABE中,sin∠EAB=,
∴AB==0.52×≈0.52×1.4≈0.7(km),
∴AB+BC+CD≈0.7+2+2≈4.7(km).
答:从A地跑到D地的路程大约是4.7km.
15.解:过点D作DE⊥AC,垂足为E,如图所示:
在Rt△ABE中,AD=60km,∠ADE=26°,
∴DE=AD?cos∠ADE=60×cos26°≈60×0.9=54(km),
∵∠DBE=45°,∠DEB=90°,
∴BE=DE=54km,
∵∠C=37°,
∴,
∴CE=.
∴CE≈54÷0.75=72(km),
∴BC=CE﹣BE=72﹣54=18(km),
答:两个观察点B,C相距的距离为18海里.
16.解:设巡逻船从出发到成功拦截所用时间为x小时;如图所示,
由题意得:∠ABC=45°+75°=120°,AB=12,BC=10x,AC=14x,
过点A作AD⊥CB的延长线于点D,
在Rt△ABD中,AB=12,∠ABD=45°+(90°﹣75°)=60°,
∴BD=AB?cos60°=AB=6,AD=AB?sin60°=6,
∴CD=10x+6.
在Rt△ACD中,由勾股定理得:,
解得:(不合题意舍去).
答:巡逻船从出发到成功拦截所用时间为2小时.
17.解:过点A作AM∥BD,过B点作BM⊥BD,AM与BM交于点M,
∵在A点测得C点在A点的北偏西75°方向,
∴∠NAC=75°,
∴∠CAM=15°,
∵由A点向南偏西45°方向行走到达B点,
∴∠MAB=45°,
∴∠MBA=45°,
∵C点在B点的北偏西45°方向,
∴∠CBM=45°,
∴∠CBA=90°,∠CBD=45°,
∵C点在D点的北偏东22.5°方向,
∴∠PDC=22.5°,
∴∠DCB=67.5°,
∴∠BDC=180°﹣67.5°﹣45°=67.5°,
∴BD=BC,
由题可得DB=2km,
∴BC=2km,
在Rt△ABC中,∠CAB=15°+45°=60°,BC=2,
∴AC=≈1.3km.
18.解:(1)依题意知:∠PAB=45°,∠PBG=15°,∠GBC=75°,
过点B作BD⊥AP于D点,
∵∠DAB=45°,,
∴AD=BD=4,
∵∠ABD=∠GBD=45°,∠GBP=15°,
∴∠PBD=60°,
∵BD=4,
∴,
∴PA=(4+4)(km);
(2)∵∠PBD=60°,BD=4,
∴PB=8,
过点P作PE⊥BC于E,
∵∠PBG=15°,∠GBC=75°,
∴∠PBE=60°,
∵PB=8,
∴BE=4,,
∵BC=12,
∴CE=8,
∴PC=4(km).
19.解:过D作DE⊥AB于E,DF⊥BC于F,如图所示:
由题意得:∠CDF=37°,CD=200米,
在Rt△CDF中,sin∠CDF==sin37°≈0.60,cos∠CDF==cos37°≈0.80,
∴CF≈200×0.60=120(米),DF≈200×0.80=160(米),
∵AB⊥BC,DF⊥BC,DE⊥AB,
∴∠B=∠DFB=∠DEB=90°,
∴四边形BFDE是矩形,
∴BF=DE,BE=DF=160米,
∴AE=AB﹣BE=300﹣160=140(米),
在Rt△ADE中,tan∠DAE==tan65°≈2.14,
∴DE≈AE×2.14=140×2.14=299.60(米),
∴BF=DE≈299.60(米),
∴BC=BF+CF=299.60+120≈420(米),
答:革命纪念碑与党史纪念馆之间的距离约为420米.
20.解:AC=AB+BC=4+6=10(km),
在Rt△ACM中,tan∠CAM==tan36.9°≈0.75,
∴CM≈7.5(km),
在Rt△BCN中,tan∠CBN==tan67.4°≈2.40,
∴CN≈14.4(km),
∴MN=CN﹣CM≈14.4﹣7.5=6.9(km).
答:该岛屿东西两端M,N之间的距离约为6.9km.
