5.2 三角形的面积(课件) 数学五年级上册-西师大版(共21张PPT)
文档属性
| 名称 | 5.2 三角形的面积(课件) 数学五年级上册-西师大版(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 08:18:10 | ||
图片预览






文档简介
(共21张PPT)
三角形面积的计算
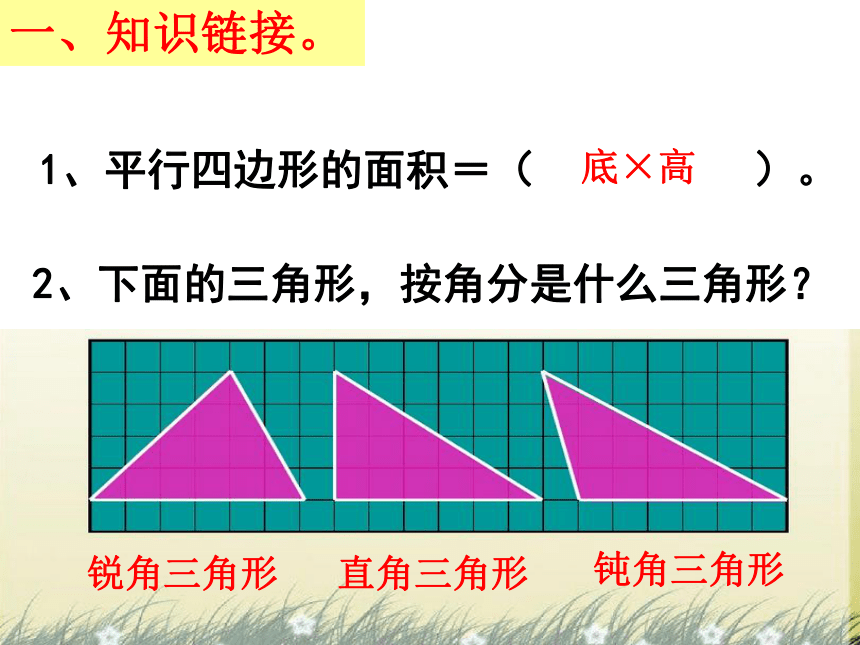
1、平行四边形的面积=(
)。
一、知识链接。
2、下面的三角形,按角分是什么三角形?
底×高
锐角三角形
直角三角形
钝角三角形
8厘米
大胆猜一猜:
下面三角形的面积是多少平方厘米?
4厘米
4厘米
8厘米
32平方厘米
?
(一)自主学习
二、学。
6×4=24(平方厘米)
计算下面这个平行四边形的面积。如果去掉平行四边形的一半,只求涂色部分图形三角形的面积,你会吗?
(1)平行四边形的面积:
(2)涂色部分三角形的面积:
涂色部分三角形的底(
??)平行四边形的底;
涂色部分三角形的高(?
?)平行四边形的高;
涂色的三角形的面积正好是平行四边形的面积的(
)
平行四边形的面积
=
(
)。
我猜想:
三角形的面积
=
(
)
24÷2=12(平方厘米)
等于
等于
一半
底×高
底×高÷2
(二)合作探究。
★活动一:
同桌合作:玩一玩手中的两个三角形,看能拼成什么我们熟悉的图形。
思考:
1)拼得的图形的底与所用三角形的底有什么关系??????
2)拼得的图形的高与所用三角形的高有什么关系?
3)其中一个三角形的面积与拼得的图形的面积有什么关系?
长方形
平行四边形
┓
┓
┓
┓
┓
┓
┓
┓
┓
┓
┓
┓
┓
┓
平行四边形
┓
平行四边形
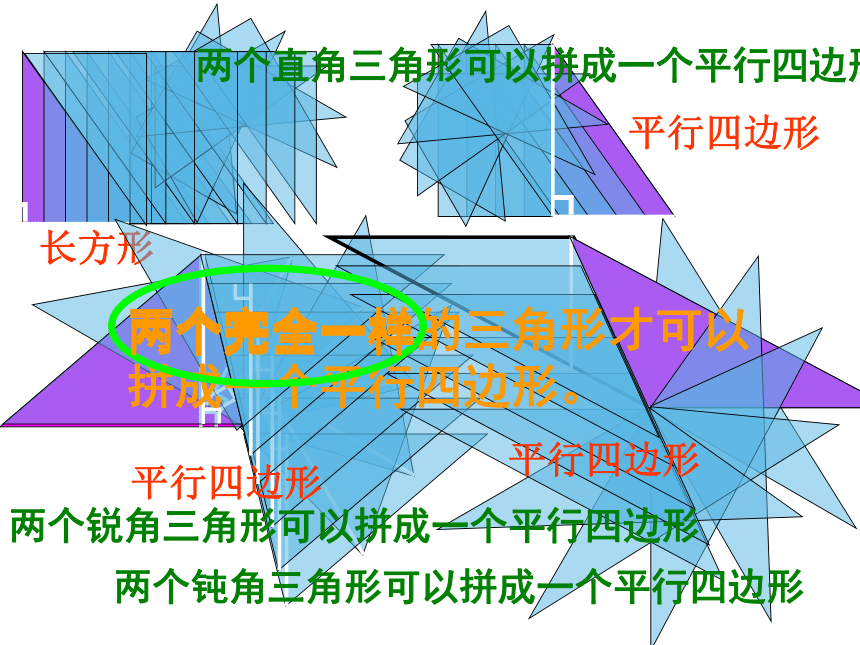
两个直角三角形可以拼成一个平行四边形
两个锐角三角形可以拼成一个平行四边形
两个钝角三角形可以拼成一个平行四边形
两个完全一样的三角形才可以拼成一个平行四边形。
两个完全一样
(二)合作探究。
★活动二:
小组合作:
1)仔细观察比较,你有什么发现?
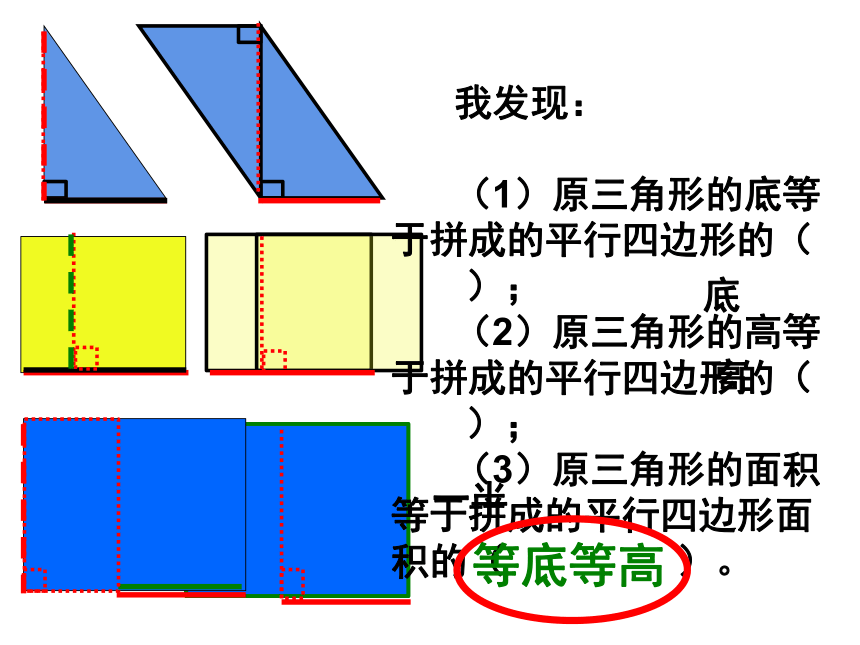
我发现:
(1)原三角形的底等于拼成的平行四边形的(???????);?
(2)原三角形的高等于拼成的平行四边形的(???????);?
(3)原三角形的面积等于拼成的平行四边形面积的(???????)。
2)根据上面的发现,我能推导出三角形的面积公式。
因为:平行四边形的面积=(??
??)×(????)
???????????????
三角形面积
=
平行四边形面积
÷
(???
?)
?
???????所以:三角形的面积=(??
???)×(???
?)÷(???
?)
3)要计算三角形的面积,必须知道它的(?????)和(???????)。
我发现:
(1)原三角形的底等于拼成的平行四边形的(???????);?
(2)原三角形的高等于拼成的平行四边形的(???????);?
(3)原三角形的面积等于拼成的平行四边形面积的(??????
?)。
底
高
一半
等底
等高
三角形的面积等于与它等底等高
的平行四边形面积的一半。
因为:平行四边形的面积
=(????)×(????)
三角形的面积
=
平行四边形面积÷(
?)
(等底等高)
2
所以:三角形的面积=(?????)×(????)÷(????)
底
×
高
2
底
×
高
想一想:求三角形的面积必须知道哪两个条件?
必须知道三角形的底和对应的高。
三角形的面积=底×高÷2
抢答:求下面三角形的面积。
6
dm
2
dm
5m
4m
3m
(二)合作探究。
★活动三:
1、2、3组探究完成3题
4、5、6组探究完成2题
7、8、9组探究完成1题
自己组完成后可以思考其他组探究的问题。
1、比较下列三角形的面积。
三角形A的底是(
)cm,高是(
)cm,面积是(
)cm2。
三角形B的底是(
),高是(
),面积是(
)。
三角形C的底是(
),高是(
),面积是(
)。
三角形A、B和C的底(
),高(
),面积就(
)。
(二)合作探究。
★活动三:
结论:等底等高的三角形的面积(
)。
相等
底:5cm
4cm
5
5
5
4
4
4
10
10
10
相等
相等
相等
(二)合作探究。
★活动三:
2、一个三角形的面积是24
dm2,底是6dm,
高是多少dm?
6dm
24dm2
?
等底等高的平行四边形
24×2=48(dm2
)
48÷6=8(dm)
三角形的高
=
三角形的面积×2÷底
三角形的底
=
三角形的面积×2÷高
(二)合作探究。
★活动三:
3、一个三角形与一个平行四边形面积相等,底相等,已知平行四边的高是16cm,三角形的高是(
)cm。
A、8
B、32
C、16
D、无法确定
结论:当一个三角形和一个平行四边形等底等面积的时候,三角形的高是平行四边形高的(
)。
2倍
B
通过今天的学习,你有什么收获?
五、练
★达标测评
:
每组的1、2、3号学生完成第1题和第3题
每组的4、5、6、7号学生完成第1题和第2题,
古代数学名著《九章算术》记载,
大约在2000年前,三角形面积公式就已经在土地的测量中使用。世界十大数学家之一、被称作“中国数学史上的牛顿”的山东人刘徽,就曾经用一个三角形推导出了它面积的计算公式。
数学文化:欣赏
传承
拓展:
你还有其他方法推导出三角形的面积公式吗?试试只用一个三角形,把它转化成我们学过的图形吗?试着把你转化的过程写下来,并说说你又能发现什么?
我的方法是:(
)
?????????????????????????????????????????????????????????????????????????????????????????????????????????????????
我的发现是:
(
)
通过今天的学习,你有什么收获?
愿同学们乘风破浪,
在数学的海洋里自由翱翔,驶向成功的彼岸。
三角形面积的计算
1、平行四边形的面积=(
)。
一、知识链接。
2、下面的三角形,按角分是什么三角形?
底×高
锐角三角形
直角三角形
钝角三角形
8厘米
大胆猜一猜:
下面三角形的面积是多少平方厘米?
4厘米
4厘米
8厘米
32平方厘米
?
(一)自主学习
二、学。
6×4=24(平方厘米)
计算下面这个平行四边形的面积。如果去掉平行四边形的一半,只求涂色部分图形三角形的面积,你会吗?
(1)平行四边形的面积:
(2)涂色部分三角形的面积:
涂色部分三角形的底(
??)平行四边形的底;
涂色部分三角形的高(?
?)平行四边形的高;
涂色的三角形的面积正好是平行四边形的面积的(
)
平行四边形的面积
=
(
)。
我猜想:
三角形的面积
=
(
)
24÷2=12(平方厘米)
等于
等于
一半
底×高
底×高÷2
(二)合作探究。
★活动一:
同桌合作:玩一玩手中的两个三角形,看能拼成什么我们熟悉的图形。
思考:
1)拼得的图形的底与所用三角形的底有什么关系??????
2)拼得的图形的高与所用三角形的高有什么关系?
3)其中一个三角形的面积与拼得的图形的面积有什么关系?
长方形
平行四边形
┓
┓
┓
┓
┓
┓
┓
┓
┓
┓
┓
┓
┓
┓
平行四边形
┓
平行四边形
两个直角三角形可以拼成一个平行四边形
两个锐角三角形可以拼成一个平行四边形
两个钝角三角形可以拼成一个平行四边形
两个完全一样的三角形才可以拼成一个平行四边形。
两个完全一样
(二)合作探究。
★活动二:
小组合作:
1)仔细观察比较,你有什么发现?
我发现:
(1)原三角形的底等于拼成的平行四边形的(???????);?
(2)原三角形的高等于拼成的平行四边形的(???????);?
(3)原三角形的面积等于拼成的平行四边形面积的(???????)。
2)根据上面的发现,我能推导出三角形的面积公式。
因为:平行四边形的面积=(??
??)×(????)
???????????????
三角形面积
=
平行四边形面积
÷
(???
?)
?
???????所以:三角形的面积=(??
???)×(???
?)÷(???
?)
3)要计算三角形的面积,必须知道它的(?????)和(???????)。
我发现:
(1)原三角形的底等于拼成的平行四边形的(???????);?
(2)原三角形的高等于拼成的平行四边形的(???????);?
(3)原三角形的面积等于拼成的平行四边形面积的(??????
?)。
底
高
一半
等底
等高
三角形的面积等于与它等底等高
的平行四边形面积的一半。
因为:平行四边形的面积
=(????)×(????)
三角形的面积
=
平行四边形面积÷(
?)
(等底等高)
2
所以:三角形的面积=(?????)×(????)÷(????)
底
×
高
2
底
×
高
想一想:求三角形的面积必须知道哪两个条件?
必须知道三角形的底和对应的高。
三角形的面积=底×高÷2
抢答:求下面三角形的面积。
6
dm
2
dm
5m
4m
3m
(二)合作探究。
★活动三:
1、2、3组探究完成3题
4、5、6组探究完成2题
7、8、9组探究完成1题
自己组完成后可以思考其他组探究的问题。
1、比较下列三角形的面积。
三角形A的底是(
)cm,高是(
)cm,面积是(
)cm2。
三角形B的底是(
),高是(
),面积是(
)。
三角形C的底是(
),高是(
),面积是(
)。
三角形A、B和C的底(
),高(
),面积就(
)。
(二)合作探究。
★活动三:
结论:等底等高的三角形的面积(
)。
相等
底:5cm
4cm
5
5
5
4
4
4
10
10
10
相等
相等
相等
(二)合作探究。
★活动三:
2、一个三角形的面积是24
dm2,底是6dm,
高是多少dm?
6dm
24dm2
?
等底等高的平行四边形
24×2=48(dm2
)
48÷6=8(dm)
三角形的高
=
三角形的面积×2÷底
三角形的底
=
三角形的面积×2÷高
(二)合作探究。
★活动三:
3、一个三角形与一个平行四边形面积相等,底相等,已知平行四边的高是16cm,三角形的高是(
)cm。
A、8
B、32
C、16
D、无法确定
结论:当一个三角形和一个平行四边形等底等面积的时候,三角形的高是平行四边形高的(
)。
2倍
B
通过今天的学习,你有什么收获?
五、练
★达标测评
:
每组的1、2、3号学生完成第1题和第3题
每组的4、5、6、7号学生完成第1题和第2题,
古代数学名著《九章算术》记载,
大约在2000年前,三角形面积公式就已经在土地的测量中使用。世界十大数学家之一、被称作“中国数学史上的牛顿”的山东人刘徽,就曾经用一个三角形推导出了它面积的计算公式。
数学文化:欣赏
传承
拓展:
你还有其他方法推导出三角形的面积公式吗?试试只用一个三角形,把它转化成我们学过的图形吗?试着把你转化的过程写下来,并说说你又能发现什么?
我的方法是:(
)
?????????????????????????????????????????????????????????????????????????????????????????????????????????????????
我的发现是:
(
)
通过今天的学习,你有什么收获?
愿同学们乘风破浪,
在数学的海洋里自由翱翔,驶向成功的彼岸。
