2021-2022学年青岛版九年级数学上册 1.3相似三角形的性质 同步优生辅导训练 (word版含解析)
文档属性
| 名称 | 2021-2022学年青岛版九年级数学上册 1.3相似三角形的性质 同步优生辅导训练 (word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 164.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 00:00:00 | ||
图片预览



文档简介
2021-2022年青岛版九年级数学上册《1.3相似三角形的性质》同步优生辅导训练(附答案)
一、选择题
1.如图,在△ABC中,CD,BE分别是△ABC的边AB,AC上的中线,则=( )
A.
B.
C.
D.
2.如果两个相似三角形的相似比为4:3,那么这两个相似三角形的面积比为( )
A.2:
B.4:3
C.16:9
D.256:81
3.在一张缩印出来的纸上,一个三角形的一条边由原图中的6cm变成了2cm,则缩印出的三角形的面积是原图中三角形面积的( )
A.
B.
C.
D.
4.已知△ABC∽△DEF,若周长比为4:9,则AC:DF等于( )
A.4:9
B.16:81
C.3:5
D.2:3
5.若△ABC∽△DEF,且对应高线比为4:9,则△ABC与△DEF的周长比为( )
A.2:3
B.3:2
C.4:9
D.16:81
6.如图,已知△ADE∽△ACB,若AB=10,AC=8,AD=4,则AE的长是( )
A.4
B.5
C.20
D.3.2
7.已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( )
A.3
B.2
C.4
D.5
8.已知△ABC∽△A1B1C1,且∠A=60°,∠B1=40°,则∠C1的度数为( )
A.40°
B.60°
C.80°
D.100°
9.两相似三角形的相似比为2:3,它们的面积之差为15,则面积之和是( )
A.39
B.75
C.76
D.40
10.如图,点D、E分别在△ABC的两边BA、CA的延长线上,下列条件能判定ED∥BC的是( )
A.
B.
C.AD?AB=DE?BC
D.AD?AC=AB?AE
二、填空题
11.已知△ABC∽△A′B′C′,AD和A′D′是它们的对应中线,若AD=8,A′D′=6,则△ABC与△A′B′C′的周长比是
.
12.如果两个相似三角形的周长的比等于1:3,那么它们对应高的比为
.
13.△ABC的三边长为4、5、6,与△ABC相似的△DEF的最长边为18,则△DEF的最短边为
.
14.两个相似三角形的相似比是3:4,其中较小的三角形的面积是8,则另一个三角形的面积是
.
15.如果两个相似三角形的对应高比是:2,那么它们的相似比是
.
三、解答题
16.如图,在△ABC,D,E分别是AB,AC上的点,△ADE∽△ACB,相似比为AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F,求AG与GF的比.
17.△ABC∽△A′B′C',且△ABC的三边长分别是、2、,△A'B'C'的两边长分别是,,求△A′B′C′的第三边长.
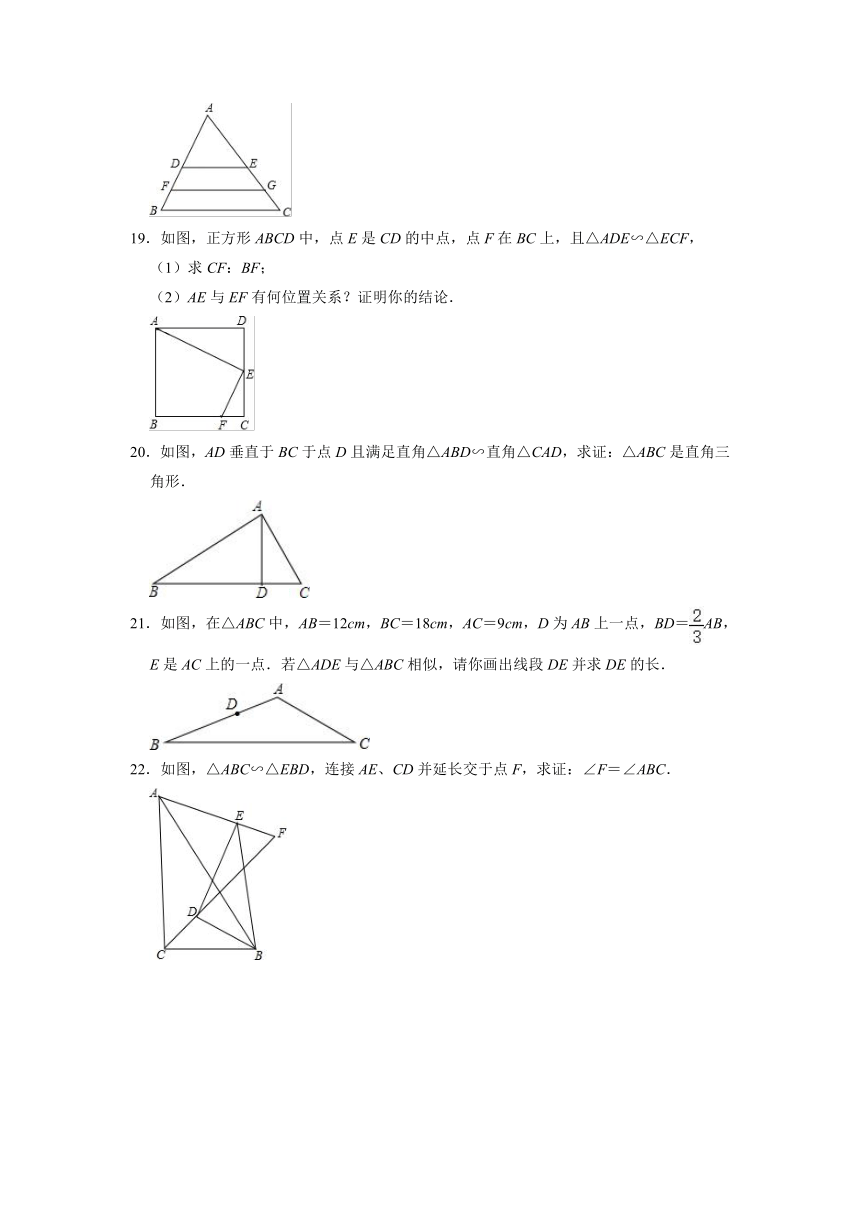
18.如图,已知△ADE∽△AFG∽△ABC,且△ABC的面积被线段DE、FG三等分,其中BC=12cm,求线段DE和FG的长度.
19.如图,正方形ABCD中,点E是CD的中点,点F在BC上,且△ADE∽△ECF,
(1)求CF:BF;
(2)AE与EF有何位置关系?证明你的结论.
20.如图,AD垂直于BC于点D且满足直角△ABD∽直角△CAD,求证:△ABC是直角三角形.
21.如图,在△ABC中,AB=12cm,BC=18cm,AC=9cm,D为AB上一点,BD=AB,E是AC上的一点.若△ADE与△ABC相似,请你画出线段DE并求DE的长.
22.如图,△ABC∽△EBD,连接AE、CD并延长交于点F,求证:∠F=∠ABC.
参考答案
1.解:∵CD,BE分别是△ABC的边AB,AC上中线,
∴D是AB的中点,E是AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∴△DEF∽△CBF,
∴==,
故选:D.
2.解:∵两个相似三角形的相似比为4:3,
∴这两个相似三角形的面积比为16:9.
故选:C.
3.解:∵三角形的一条边由原图中的6cm变成了2cm,
∴原三角形与缩印出的三角形是相似比为3:1,
∴原三角形与缩印出的三角形是面积比为9:1,
∴缩印出的三角形的面积是原图中三角形面积的,
故选:C.
4.解:∵△ABC∽△DEF,
∴==.
故选:A.
5.解:∵△ABC∽△DEF,且对应高线比为4:9,
∴△ABC与△DEF的周长比为4:9.
故选:C.
6.解:∵△ADE∽△ACB,
∴=,
∵AB=10,AC=8,AD=4,
∴=,
解得:AE=5.
故选:B.
7.解:∵△FHB和△EAD的周长分别为30和15,
∴△FHB和△EAD的周长比为2:1,
∵△FHB∽△EAD,
∴=2,即=2,
解得,EA=3,
故选:A.
8.解:∵△ABC∽△A1B1C1,
∴∠A1=∠A=60°,∠B=∠B1=40°,
则∠C1=180°﹣60°﹣40°=80°.
故选:C.
9.解:∵这两个相似三角形的相似比为2:3,
∴它们的面积比为:4:9,
设此两个三角形的面积分别为4xcm2,9xcm2,
∵它们的面积之差为15cm2,
∴9x﹣4x=15,
解得:x=3,
∴它们的面积之和是:9x+4x=13x=39.
故选:A.
10.解:∵∠EAD=∠CAB,
∴当,
即AD?AC=AB?AE,
∴ED∥BC,
故选:D.
11.解:∵AD=8,A′D′=6,
∴AD:A′D′=4:3,
∵△ABC∽△A′B′C′,AD和A′D′是它们的对应中线,
∴△ABC与△A′B′C′的相似比=AD:A′D′=4:3,
∴△ABC与△A′B′C′的周长比是4:3,
故答案为:4:3.
12.解:∵两个相似三角形的周长比为1:3,
∴两个相似三角形的相似比为1:3,
∴对应高线的比为:1:3,
故答案为:1:3.
13.解:设△DEF的最短边为x,
∵△ABC∽△DEF,
∴=,
解得,x=12,
故答案为:12.
14.解:∵两个相似三角形的相似比是3:4,
∴这两个相似三角形的面积比是9:16,
∵较小的三角形的面积是8,
∴另一个三角形的面积是.
故答案为:.
15.解:∵两个相似三角形的对应高比是:2,
∴它们的相似比是:2,
故答案为::2.
16.解:∵△ADE∽△ACB,
∴∠ADE=∠ACB,∠AED=∠ABC,
∵AF是∠BAC的平分线,
∴∠BAF=∠CAF,
∵∠AGD=∠CAF+∠AED,∠AFC=∠BAF+∠ABC,
∴∠AGD=∠AFC,
∴△AGD∽△AFC,
∴==,
∴AG:GF=2:1.
17.解:设△A′B′C′的第三边长为x,
∵△ABC∽△A′B′C,△ABC的三边长分别是、2、,△A'B'C'的两边长分别是,,
∴与、与是对应边,
则=,
解得,x=2,
∴△A′B′C′的第三边长为2.
18.解:∵△ADE∽△ABC,且△ABC的面积被线段DE、FG三等分,
∴()2=,
即()2=,
解得DE=4,
∵△AFG∽△ABC,且△ABC的面积被线段DE、FG三等分,
∴()2=,
即()2=,
解得FG=4,
答:线段DE和FG的长度分别为4cm,4cm.
19.即:(1)∵点E是CD的中点,
∴DE=CE.
∵△ADE∽△ECF,
∴==;
(2)AE⊥EF.
理由:∵△ADE∽△ECF,
∴∠CEF=∠DAE.
∵∠AED+∠DAE=90°,
∴∠AED+∠CEF=90°,即AE⊥EF.
20.解:∵直角△ABD∽直角△CAD,
∴∠BAD=∠C,
∵AD⊥BC,
∴∠DAC+∠C=90°,
∴∠DAC+∠BAD=90°,
∴∠BAC=90°,
∴△ABC是直角三角形.
21.解:如图1,△ADE∽△ABC,
∴=,
又∵BD=AB,AB=12cm,BC=18cm,
∴DE=6cm;
如图2,△ADE∽△ACB,
∴=,
∵BD=AB,AB=12cm,
∴AD=4cm,
又∵BC=18cm,
∴DE=8cm.
答:DE的长是6cm或8cm.
22.证明:如图,
∵△ABC∽△EBD,
∴=,∠ABC=∠EBD,
即=,∠1+∠2=∠2+∠3,
∴∠1=∠3,
∴△BCD∽△BAE,
∴∠5=∠6,
而∠7=∠8,
∴∠F=∠ABC.
一、选择题
1.如图,在△ABC中,CD,BE分别是△ABC的边AB,AC上的中线,则=( )
A.
B.
C.
D.
2.如果两个相似三角形的相似比为4:3,那么这两个相似三角形的面积比为( )
A.2:
B.4:3
C.16:9
D.256:81
3.在一张缩印出来的纸上,一个三角形的一条边由原图中的6cm变成了2cm,则缩印出的三角形的面积是原图中三角形面积的( )
A.
B.
C.
D.
4.已知△ABC∽△DEF,若周长比为4:9,则AC:DF等于( )
A.4:9
B.16:81
C.3:5
D.2:3
5.若△ABC∽△DEF,且对应高线比为4:9,则△ABC与△DEF的周长比为( )
A.2:3
B.3:2
C.4:9
D.16:81
6.如图,已知△ADE∽△ACB,若AB=10,AC=8,AD=4,则AE的长是( )
A.4
B.5
C.20
D.3.2
7.已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( )
A.3
B.2
C.4
D.5
8.已知△ABC∽△A1B1C1,且∠A=60°,∠B1=40°,则∠C1的度数为( )
A.40°
B.60°
C.80°
D.100°
9.两相似三角形的相似比为2:3,它们的面积之差为15,则面积之和是( )
A.39
B.75
C.76
D.40
10.如图,点D、E分别在△ABC的两边BA、CA的延长线上,下列条件能判定ED∥BC的是( )
A.
B.
C.AD?AB=DE?BC
D.AD?AC=AB?AE
二、填空题
11.已知△ABC∽△A′B′C′,AD和A′D′是它们的对应中线,若AD=8,A′D′=6,则△ABC与△A′B′C′的周长比是
.
12.如果两个相似三角形的周长的比等于1:3,那么它们对应高的比为
.
13.△ABC的三边长为4、5、6,与△ABC相似的△DEF的最长边为18,则△DEF的最短边为
.
14.两个相似三角形的相似比是3:4,其中较小的三角形的面积是8,则另一个三角形的面积是
.
15.如果两个相似三角形的对应高比是:2,那么它们的相似比是
.
三、解答题
16.如图,在△ABC,D,E分别是AB,AC上的点,△ADE∽△ACB,相似比为AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F,求AG与GF的比.
17.△ABC∽△A′B′C',且△ABC的三边长分别是、2、,△A'B'C'的两边长分别是,,求△A′B′C′的第三边长.
18.如图,已知△ADE∽△AFG∽△ABC,且△ABC的面积被线段DE、FG三等分,其中BC=12cm,求线段DE和FG的长度.
19.如图,正方形ABCD中,点E是CD的中点,点F在BC上,且△ADE∽△ECF,
(1)求CF:BF;
(2)AE与EF有何位置关系?证明你的结论.
20.如图,AD垂直于BC于点D且满足直角△ABD∽直角△CAD,求证:△ABC是直角三角形.
21.如图,在△ABC中,AB=12cm,BC=18cm,AC=9cm,D为AB上一点,BD=AB,E是AC上的一点.若△ADE与△ABC相似,请你画出线段DE并求DE的长.
22.如图,△ABC∽△EBD,连接AE、CD并延长交于点F,求证:∠F=∠ABC.
参考答案
1.解:∵CD,BE分别是△ABC的边AB,AC上中线,
∴D是AB的中点,E是AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∴△DEF∽△CBF,
∴==,
故选:D.
2.解:∵两个相似三角形的相似比为4:3,
∴这两个相似三角形的面积比为16:9.
故选:C.
3.解:∵三角形的一条边由原图中的6cm变成了2cm,
∴原三角形与缩印出的三角形是相似比为3:1,
∴原三角形与缩印出的三角形是面积比为9:1,
∴缩印出的三角形的面积是原图中三角形面积的,
故选:C.
4.解:∵△ABC∽△DEF,
∴==.
故选:A.
5.解:∵△ABC∽△DEF,且对应高线比为4:9,
∴△ABC与△DEF的周长比为4:9.
故选:C.
6.解:∵△ADE∽△ACB,
∴=,
∵AB=10,AC=8,AD=4,
∴=,
解得:AE=5.
故选:B.
7.解:∵△FHB和△EAD的周长分别为30和15,
∴△FHB和△EAD的周长比为2:1,
∵△FHB∽△EAD,
∴=2,即=2,
解得,EA=3,
故选:A.
8.解:∵△ABC∽△A1B1C1,
∴∠A1=∠A=60°,∠B=∠B1=40°,
则∠C1=180°﹣60°﹣40°=80°.
故选:C.
9.解:∵这两个相似三角形的相似比为2:3,
∴它们的面积比为:4:9,
设此两个三角形的面积分别为4xcm2,9xcm2,
∵它们的面积之差为15cm2,
∴9x﹣4x=15,
解得:x=3,
∴它们的面积之和是:9x+4x=13x=39.
故选:A.
10.解:∵∠EAD=∠CAB,
∴当,
即AD?AC=AB?AE,
∴ED∥BC,
故选:D.
11.解:∵AD=8,A′D′=6,
∴AD:A′D′=4:3,
∵△ABC∽△A′B′C′,AD和A′D′是它们的对应中线,
∴△ABC与△A′B′C′的相似比=AD:A′D′=4:3,
∴△ABC与△A′B′C′的周长比是4:3,
故答案为:4:3.
12.解:∵两个相似三角形的周长比为1:3,
∴两个相似三角形的相似比为1:3,
∴对应高线的比为:1:3,
故答案为:1:3.
13.解:设△DEF的最短边为x,
∵△ABC∽△DEF,
∴=,
解得,x=12,
故答案为:12.
14.解:∵两个相似三角形的相似比是3:4,
∴这两个相似三角形的面积比是9:16,
∵较小的三角形的面积是8,
∴另一个三角形的面积是.
故答案为:.
15.解:∵两个相似三角形的对应高比是:2,
∴它们的相似比是:2,
故答案为::2.
16.解:∵△ADE∽△ACB,
∴∠ADE=∠ACB,∠AED=∠ABC,
∵AF是∠BAC的平分线,
∴∠BAF=∠CAF,
∵∠AGD=∠CAF+∠AED,∠AFC=∠BAF+∠ABC,
∴∠AGD=∠AFC,
∴△AGD∽△AFC,
∴==,
∴AG:GF=2:1.
17.解:设△A′B′C′的第三边长为x,
∵△ABC∽△A′B′C,△ABC的三边长分别是、2、,△A'B'C'的两边长分别是,,
∴与、与是对应边,
则=,
解得,x=2,
∴△A′B′C′的第三边长为2.
18.解:∵△ADE∽△ABC,且△ABC的面积被线段DE、FG三等分,
∴()2=,
即()2=,
解得DE=4,
∵△AFG∽△ABC,且△ABC的面积被线段DE、FG三等分,
∴()2=,
即()2=,
解得FG=4,
答:线段DE和FG的长度分别为4cm,4cm.
19.即:(1)∵点E是CD的中点,
∴DE=CE.
∵△ADE∽△ECF,
∴==;
(2)AE⊥EF.
理由:∵△ADE∽△ECF,
∴∠CEF=∠DAE.
∵∠AED+∠DAE=90°,
∴∠AED+∠CEF=90°,即AE⊥EF.
20.解:∵直角△ABD∽直角△CAD,
∴∠BAD=∠C,
∵AD⊥BC,
∴∠DAC+∠C=90°,
∴∠DAC+∠BAD=90°,
∴∠BAC=90°,
∴△ABC是直角三角形.
21.解:如图1,△ADE∽△ABC,
∴=,
又∵BD=AB,AB=12cm,BC=18cm,
∴DE=6cm;
如图2,△ADE∽△ACB,
∴=,
∵BD=AB,AB=12cm,
∴AD=4cm,
又∵BC=18cm,
∴DE=8cm.
答:DE的长是6cm或8cm.
22.证明:如图,
∵△ABC∽△EBD,
∴=,∠ABC=∠EBD,
即=,∠1+∠2=∠2+∠3,
∴∠1=∠3,
∴△BCD∽△BAE,
∴∠5=∠6,
而∠7=∠8,
∴∠F=∠ABC.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
