2021-2022学年青岛版九年级数学上册 1.1相似多边形 同步训练 (word版含解析)
文档属性
| 名称 | 2021-2022学年青岛版九年级数学上册 1.1相似多边形 同步训练 (word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 156.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 00:55:33 | ||
图片预览



文档简介
2021-2022学年青岛版九年级数学上册《1.1相似多边形》同步优生辅导训练(附答案)
一、选择题
1.下列图形中不一定相似的是( )
A.两个矩形
B.两个圆
C.两个正方形
D.两个等边三角形
2.如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为( )
A.70°
B.80°
C.90°
D.120°
3.在10倍的放大镜下看到的三角形与原三角形相比,三角形的周长( )
A.没有发生变化
B.放大了10倍
C.放大了30倍
D.放大了100倍
4.下列说法中,错误的是( )
A.全等图形一定是相似图形
B.两个等边三角形一定相似
C.两个等腰直角三角形一定相似
D.两个直角三角形一定相似
5.下列各组图形中,一定相似的是( )
A.两个等腰三角形
B.两个等边三角形
C.两个平行四边形
D.两个菱形
6.下列说法错误的是( )
A.等边三角形都相似
B.矩形都相似
C.等腰直角三角形都相似
D.正方形都相似
7.下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )
A.
B.
C.
D.
8.下列说法中,正确的是( )
A.两个矩形必相似
B.两个含45°角的等腰三角形必相似
C.两个菱形必相似
D.两个含30°角的直角三角形必相似
9.两个相似多边形的一组对应边分别是3cm和4.5cm,如果它们的周长之和是80cm,那么较大的多边形的周长是( )
A.16cm
B.32cm
C.48cm
D.52cm
10.如图,四边形ABCD∽四边形EFGH,则下列角的度数正确的是( )
A.∠D=81°
B.∠F=83°
C.∠G=78°
D.∠H=76°
11.若四边形ABCD与四边形A′B′C′D′相似,AB与A′B′,AD与A′D′分别是对应边,AB=8cm,A′B′=6cm,AD=5cm,则A′D′等于( )
A.cm
B.cm
C.cm
D.cm
12.如图,已知矩形ABCD中,AB=3,BE=2,EF⊥BC.若四边形EFDC与四边形BEFA相似而不全等,则CE=( )
A.3
B.3.5
C.4
D.4.5
13.若一个多边形的各边长分别为2,3,4,5,6,另一个和它相似的多边形的最长边长为24,则另一个多边形的最短边长为( )
A.6
B.8
C.10
D.12
14.如图,在矩形ABCD中,点E,F分别是AD,BC边的中点,连接EF,若矩形ABFE与矩形ABCD相似,AB=1,则矩形ABCD的面积为( )
A.1
B.
C.
D.2
15.如图,将一张矩形纸片沿较长边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么我们把这样的纸张叫做标准纸.则标准纸的宽和长的比值为( )
A.
B.
C.
D.
16.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )
A.
B.
C.
D.
17.如图所示的四边形,与选项中的四边形一定相似的是( )
A.
B.
C.
D.
18.两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为( )
A.
B.
C.
D.
19.若矩形ABCD∽矩形EFGH,相似比为2:3,已知AB=3cm,BC=5cm,则矩形EFGH的周长是( )
A.16cm
B.12cm
C.24cm
D.36cm
20.在矩形ABCD中,AB=1,BC=m(m>1),将此矩形对折,使得边AB与CD重合.如果对折后得到的矩形与原矩形相似,那么m等于( )
A.
B.2
C.
D.
21.如图,矩形相框的外框矩形的长为12dm,宽为8dm,上下边框的宽度都为xdm,左右边框的宽度都为ydm.则符合下列条件的x,y的值能使内边框矩形和外边框矩形相似的为( )
A.x=y
B.3x=2y
C.x=1,y=2
D.x=3,y=2
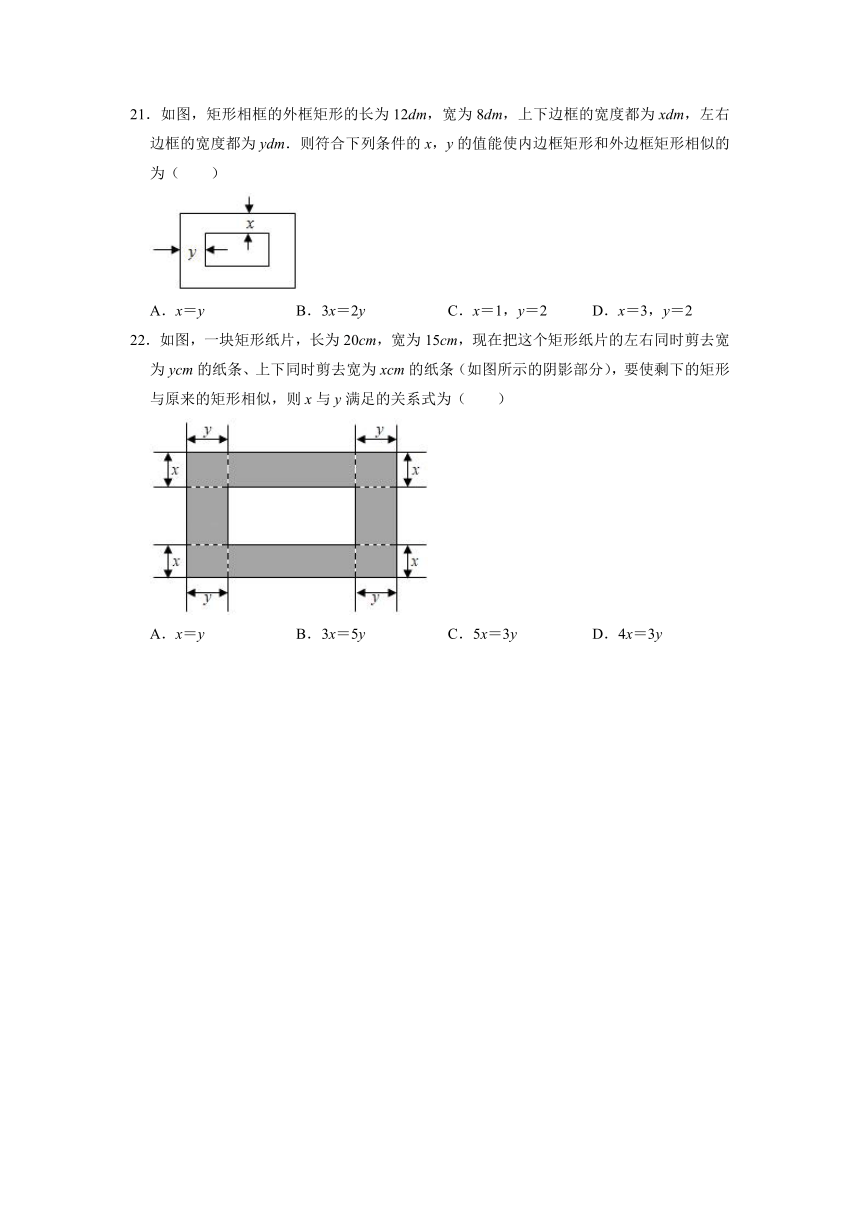
22.如图,一块矩形纸片,长为20cm,宽为15cm,现在把这个矩形纸片的左右同时剪去宽为ycm的纸条、上下同时剪去宽为xcm的纸条(如图所示的阴影部分),要使剩下的矩形与原来的矩形相似,则x与y满足的关系式为( )
A.x=y
B.3x=5y
C.5x=3y
D.4x=3y
参考答案
1.解:A.所有的矩形,对应边不一定成比例,对应角一定相等,故不一定相似,故本选项符合题意;
B.所有的圆,一定相似,故本选项不合题意;
C.所有的正方形对应边成比例,对应角相等,一定相似,故本选项不合题意;
D.所有的等边三角形对应边成比例,对应角相等,一定相似,故本选项不合题意.
故选:A.
2.解:∵四边形ABCD∽四边形EFGH,∠A=80°,
∴∠E=∠A=80°,
故选:B.
3.解:在10倍的放大镜下看到的三角形与原三角形相比,则边长扩大10倍,故三角形的周长放大了10倍.
故选:B.
4.解:A、全等图形一定是相似图形,正确,不合题意;
B、两个等边三角形一定相似,正确,不合题意;
C、两个等腰直角三角形一定相似,正确,不合题意;
D、两个直角三角形不一定相似,原说法错误,故此选项符合题意.
故选:D.
5.解:A、任意两个等腰三角形的对应边的比相等,但对应角不一定相等,故不一定相似,不符合题意;
B、任意两个等边三角形的对应角相等,对应边的比也相等,故一定相似,符合题意;
C、任意两个平行四边形对应角不一定相等,对应边的比也不一定相等,故不一定相似,不符合题意,
D、任意两个菱形的对应边的比相等,但对应角不一定相等,故不一定相似,不符合题意;
故选:B.
6.解:因为所有等边三角形,正方形,等腰直角三角形都相似,
故选:B.
7.解:A、两图形形状相同,是相似图形,不符合题意;
B、两图形形状不同,不是相似图形,符合题意;
C、两图形形状相同,是相似图形,不符合题意;
D、两图形形状相同,是相似图形,不符合题意;
故选:B.
8.解:A、两个矩形对应边不一定成比例,故此选项错误;
B、两个含45°角的等腰三角形,45°不一定是对应角,故不一定相似,故此选项错误;
C、两个菱形的对应角不一定相等,不一定相似,故此选项错误;
D、两个含30°角的直角三角形必相似,故此选项正确.
故选:D.
9.解:设较大多边形与较小多边形的周长分别是m,n.则==.
因而n=m.
根据周长之和是80cm.得到m+m=80.
解得:m=48cm.
故选:C.
10.解:∵四边形ABCD和四边形EFGH相似,
∴∠B=∠F=78°,∠A=∠E=118°,∠C=∠G=88°,
∴∠D=360°﹣78°﹣118°﹣88°=76°.
故选:D.
11.解:∵四边形ABCD与四边形A′B′C′D′相似,AB与A′B′,AD与A′D′分别是对应边,
∴=,
∵AB=8cm,A′B′=6cm,AD=5cm,
∴=,
则A′D′=.
故选:B.
12.解:设CE=x,
∵四边形EFDC与四边形BEFA相似,
∴,
∵AB=3,BE=2,EF=AB,
∴,
解得:x=4.5,
故选:D.
13.解:设这个多边形的最短边长为x,
∵两个多边形相似,
∴,
解得,x=8,
故选:B.
14.解:设AE=x,则AD=2AE=2x,
∵矩形ABFE与矩形ABCD相似,
∴,即,
解得,x=,
∴AD=2x=,
∴矩形ABCD的面积为AB?AD=1×=,
故选:C.
15.解:设原来矩形的长为x,宽为y,
则对折后的矩形的长为y,宽为,
∵得到的两个矩形都和原矩形相似,
∴x:y=y:,
解得y:x=.
故选:A.
16.解:由题意得,A中三角形对应角相等,对应边成比例,两三角形相似;
C,D中正方形,菱形四条边均相等,所以对应边成比例,又角也相等,所以正方形,菱形相似;
而B中矩形四个角相等,但对应边不一定成比例,所以B中矩形不是相似多边形.
故选:B.
17.解:作AE⊥BC于E,
则四边形AECD为矩形,
∴EC=AD=1,AE=CD=3,
∴BE=4,
由勾股定理得,AB==5,
∴四边形ABCD的四条边之比为1:3:5:5,
D选项中,四条边之比为1:3:5:5,且对应角相等,
故选:D.
18.解:∵两个相似多边形一组对应边分别为3cm,4.5cm,
∴它们的相似比为:=.
故选:A.
19.解:∵AB=3cm,BC=5cm,
∴矩形ABCD的周长=2×(3+5)=16cm,
∵矩形ABCD∽矩形EFGH,相似比为2:3,
∴矩形ABCD与矩形EFGH的周长比2:3,
∴矩形EFGH的周长为24cm,
故选:C.
20.解:根据矩形相似,对应边的比相等得到:=,
∴=,
∴m2=2,
∵m>0,
∴m=,
故选:A.
21.解:如图,当矩形ABCD∽矩形EFGH时,则有=,
∴=,
可得3x=2y,选项B符合题意,
当矩形ABCD∽矩形EHFG时,则有=,
∴=,
推不出:x=y或3x=2y或x=1,y=2或x=3,y=2.故选项A,B,C,D都不满足条件,此种情形不存在.
∴矩形ABCD∽矩形EFGH,可得3x=2y,
故选:B.
22.解:∵剩下的矩形与原来的矩形相似,
∴=,
整理得:30y=40x,
则4x=3y.
故选:D.
一、选择题
1.下列图形中不一定相似的是( )
A.两个矩形
B.两个圆
C.两个正方形
D.两个等边三角形
2.如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为( )
A.70°
B.80°
C.90°
D.120°
3.在10倍的放大镜下看到的三角形与原三角形相比,三角形的周长( )
A.没有发生变化
B.放大了10倍
C.放大了30倍
D.放大了100倍
4.下列说法中,错误的是( )
A.全等图形一定是相似图形
B.两个等边三角形一定相似
C.两个等腰直角三角形一定相似
D.两个直角三角形一定相似
5.下列各组图形中,一定相似的是( )
A.两个等腰三角形
B.两个等边三角形
C.两个平行四边形
D.两个菱形
6.下列说法错误的是( )
A.等边三角形都相似
B.矩形都相似
C.等腰直角三角形都相似
D.正方形都相似
7.下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )
A.
B.
C.
D.
8.下列说法中,正确的是( )
A.两个矩形必相似
B.两个含45°角的等腰三角形必相似
C.两个菱形必相似
D.两个含30°角的直角三角形必相似
9.两个相似多边形的一组对应边分别是3cm和4.5cm,如果它们的周长之和是80cm,那么较大的多边形的周长是( )
A.16cm
B.32cm
C.48cm
D.52cm
10.如图,四边形ABCD∽四边形EFGH,则下列角的度数正确的是( )
A.∠D=81°
B.∠F=83°
C.∠G=78°
D.∠H=76°
11.若四边形ABCD与四边形A′B′C′D′相似,AB与A′B′,AD与A′D′分别是对应边,AB=8cm,A′B′=6cm,AD=5cm,则A′D′等于( )
A.cm
B.cm
C.cm
D.cm
12.如图,已知矩形ABCD中,AB=3,BE=2,EF⊥BC.若四边形EFDC与四边形BEFA相似而不全等,则CE=( )
A.3
B.3.5
C.4
D.4.5
13.若一个多边形的各边长分别为2,3,4,5,6,另一个和它相似的多边形的最长边长为24,则另一个多边形的最短边长为( )
A.6
B.8
C.10
D.12
14.如图,在矩形ABCD中,点E,F分别是AD,BC边的中点,连接EF,若矩形ABFE与矩形ABCD相似,AB=1,则矩形ABCD的面积为( )
A.1
B.
C.
D.2
15.如图,将一张矩形纸片沿较长边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么我们把这样的纸张叫做标准纸.则标准纸的宽和长的比值为( )
A.
B.
C.
D.
16.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )
A.
B.
C.
D.
17.如图所示的四边形,与选项中的四边形一定相似的是( )
A.
B.
C.
D.
18.两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为( )
A.
B.
C.
D.
19.若矩形ABCD∽矩形EFGH,相似比为2:3,已知AB=3cm,BC=5cm,则矩形EFGH的周长是( )
A.16cm
B.12cm
C.24cm
D.36cm
20.在矩形ABCD中,AB=1,BC=m(m>1),将此矩形对折,使得边AB与CD重合.如果对折后得到的矩形与原矩形相似,那么m等于( )
A.
B.2
C.
D.
21.如图,矩形相框的外框矩形的长为12dm,宽为8dm,上下边框的宽度都为xdm,左右边框的宽度都为ydm.则符合下列条件的x,y的值能使内边框矩形和外边框矩形相似的为( )
A.x=y
B.3x=2y
C.x=1,y=2
D.x=3,y=2
22.如图,一块矩形纸片,长为20cm,宽为15cm,现在把这个矩形纸片的左右同时剪去宽为ycm的纸条、上下同时剪去宽为xcm的纸条(如图所示的阴影部分),要使剩下的矩形与原来的矩形相似,则x与y满足的关系式为( )
A.x=y
B.3x=5y
C.5x=3y
D.4x=3y
参考答案
1.解:A.所有的矩形,对应边不一定成比例,对应角一定相等,故不一定相似,故本选项符合题意;
B.所有的圆,一定相似,故本选项不合题意;
C.所有的正方形对应边成比例,对应角相等,一定相似,故本选项不合题意;
D.所有的等边三角形对应边成比例,对应角相等,一定相似,故本选项不合题意.
故选:A.
2.解:∵四边形ABCD∽四边形EFGH,∠A=80°,
∴∠E=∠A=80°,
故选:B.
3.解:在10倍的放大镜下看到的三角形与原三角形相比,则边长扩大10倍,故三角形的周长放大了10倍.
故选:B.
4.解:A、全等图形一定是相似图形,正确,不合题意;
B、两个等边三角形一定相似,正确,不合题意;
C、两个等腰直角三角形一定相似,正确,不合题意;
D、两个直角三角形不一定相似,原说法错误,故此选项符合题意.
故选:D.
5.解:A、任意两个等腰三角形的对应边的比相等,但对应角不一定相等,故不一定相似,不符合题意;
B、任意两个等边三角形的对应角相等,对应边的比也相等,故一定相似,符合题意;
C、任意两个平行四边形对应角不一定相等,对应边的比也不一定相等,故不一定相似,不符合题意,
D、任意两个菱形的对应边的比相等,但对应角不一定相等,故不一定相似,不符合题意;
故选:B.
6.解:因为所有等边三角形,正方形,等腰直角三角形都相似,
故选:B.
7.解:A、两图形形状相同,是相似图形,不符合题意;
B、两图形形状不同,不是相似图形,符合题意;
C、两图形形状相同,是相似图形,不符合题意;
D、两图形形状相同,是相似图形,不符合题意;
故选:B.
8.解:A、两个矩形对应边不一定成比例,故此选项错误;
B、两个含45°角的等腰三角形,45°不一定是对应角,故不一定相似,故此选项错误;
C、两个菱形的对应角不一定相等,不一定相似,故此选项错误;
D、两个含30°角的直角三角形必相似,故此选项正确.
故选:D.
9.解:设较大多边形与较小多边形的周长分别是m,n.则==.
因而n=m.
根据周长之和是80cm.得到m+m=80.
解得:m=48cm.
故选:C.
10.解:∵四边形ABCD和四边形EFGH相似,
∴∠B=∠F=78°,∠A=∠E=118°,∠C=∠G=88°,
∴∠D=360°﹣78°﹣118°﹣88°=76°.
故选:D.
11.解:∵四边形ABCD与四边形A′B′C′D′相似,AB与A′B′,AD与A′D′分别是对应边,
∴=,
∵AB=8cm,A′B′=6cm,AD=5cm,
∴=,
则A′D′=.
故选:B.
12.解:设CE=x,
∵四边形EFDC与四边形BEFA相似,
∴,
∵AB=3,BE=2,EF=AB,
∴,
解得:x=4.5,
故选:D.
13.解:设这个多边形的最短边长为x,
∵两个多边形相似,
∴,
解得,x=8,
故选:B.
14.解:设AE=x,则AD=2AE=2x,
∵矩形ABFE与矩形ABCD相似,
∴,即,
解得,x=,
∴AD=2x=,
∴矩形ABCD的面积为AB?AD=1×=,
故选:C.
15.解:设原来矩形的长为x,宽为y,
则对折后的矩形的长为y,宽为,
∵得到的两个矩形都和原矩形相似,
∴x:y=y:,
解得y:x=.
故选:A.
16.解:由题意得,A中三角形对应角相等,对应边成比例,两三角形相似;
C,D中正方形,菱形四条边均相等,所以对应边成比例,又角也相等,所以正方形,菱形相似;
而B中矩形四个角相等,但对应边不一定成比例,所以B中矩形不是相似多边形.
故选:B.
17.解:作AE⊥BC于E,
则四边形AECD为矩形,
∴EC=AD=1,AE=CD=3,
∴BE=4,
由勾股定理得,AB==5,
∴四边形ABCD的四条边之比为1:3:5:5,
D选项中,四条边之比为1:3:5:5,且对应角相等,
故选:D.
18.解:∵两个相似多边形一组对应边分别为3cm,4.5cm,
∴它们的相似比为:=.
故选:A.
19.解:∵AB=3cm,BC=5cm,
∴矩形ABCD的周长=2×(3+5)=16cm,
∵矩形ABCD∽矩形EFGH,相似比为2:3,
∴矩形ABCD与矩形EFGH的周长比2:3,
∴矩形EFGH的周长为24cm,
故选:C.
20.解:根据矩形相似,对应边的比相等得到:=,
∴=,
∴m2=2,
∵m>0,
∴m=,
故选:A.
21.解:如图,当矩形ABCD∽矩形EFGH时,则有=,
∴=,
可得3x=2y,选项B符合题意,
当矩形ABCD∽矩形EHFG时,则有=,
∴=,
推不出:x=y或3x=2y或x=1,y=2或x=3,y=2.故选项A,B,C,D都不满足条件,此种情形不存在.
∴矩形ABCD∽矩形EFGH,可得3x=2y,
故选:B.
22.解:∵剩下的矩形与原来的矩形相似,
∴=,
整理得:30y=40x,
则4x=3y.
故选:D.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
