2021-2022学年青岛版九年级数学上册 1.4图形的位似 同步能力提升训练 (word版含解析)
文档属性
| 名称 | 2021-2022学年青岛版九年级数学上册 1.4图形的位似 同步能力提升训练 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 283.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 01:10:40 | ||
图片预览




文档简介
2021-2022学年青岛版九年级数学上册《1.4图形的位似》同步能力提升训练(附答案)
一、选择题
1.已知点A的坐标是(2,1),以坐标原点O为位似中心,像与原图形的位似比为2,则点A′的坐标为( )
A.()
B.(4,2)
C.(1,)或(﹣1,)
D.(4,2)或(﹣4,﹣2)
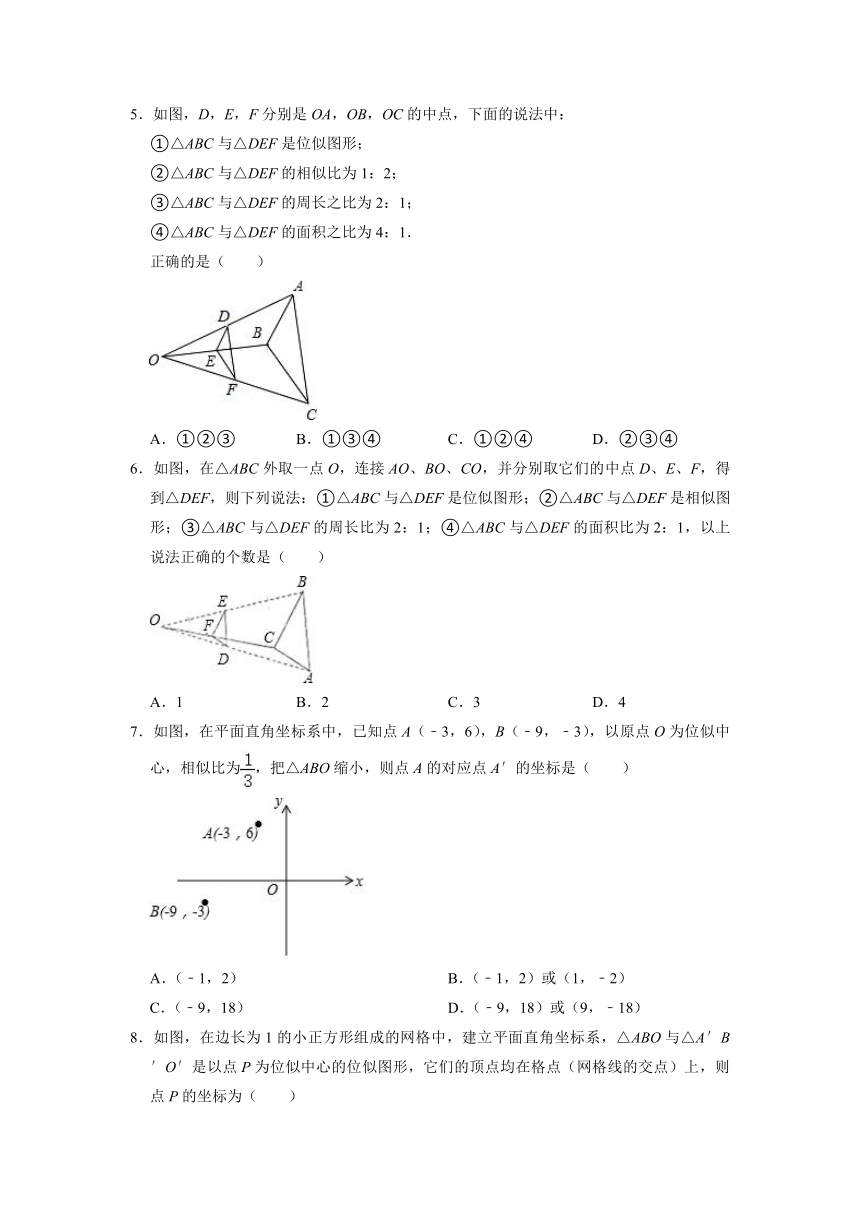
2.如图,△ABC与△DEF是位似图形,位似中心为O,OA:AD=3:4,S△ABC=9,则△DEF的面积为( )
A.12
B.16
C.21
D.49
3.如图,△ABC是△DEF以点O为位似中心经过位似变换得到的,若△ABC与△DEF的周长比为2:3,则OA与OD之比为( )
A.2:3
B.3:2
C.2:5
D.3:5
4.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且,则=( )
A.
B.
C.
D.
5.如图,D,E,F分别是OA,OB,OC的中点,下面的说法中:
①△ABC与△DEF是位似图形;
②△ABC与△DEF的相似比为1:2;
③△ABC与△DEF的周长之比为2:1;
④△ABC与△DEF的面积之比为4:1.
正确的是( )
A.①②③
B.①③④
C.①②④
D.②③④
6.如图,在△ABC外取一点O,连接AO、BO、CO,并分别取它们的中点D、E、F,得到△DEF,则下列说法:①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC与△DEF的周长比为2:1;④△ABC与△DEF的面积比为2:1,以上说法正确的个数是( )
A.1
B.2
C.3
D.4
7.如图,在平面直角坐标系中,已知点A(﹣3,6),B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(﹣1,2)
B.(﹣1,2)或(1,﹣2)
C.(﹣9,18)
D.(﹣9,18)或(9,﹣18)
8.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
A.(0,0)
B.(0,1)
C.(﹣3,2)
D.(3,﹣2)
9.如图,△ABC的顶点坐标分别为A(﹣4,2),B(﹣2,4),C(﹣4,4),以原点O为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,﹣2),则点A的对应点A′的坐标为( )
A.(2,﹣3)
B.(2,﹣1)
C.(3,﹣2)
D.(1,﹣2)
10.在平面直角坐标系中,已知两点A(7,5),B(4,3),先将线段AB向右平移1个单位,再向上平移1个单位,然后以原点O为位似中心,将其缩小为原来的,得到线段CD,则点A的对应点C的坐标为( )
A.(4,3)
B.(4,3)或(﹣4,﹣3)
C.(﹣4,﹣3)
D.(3,2)或(﹣3,﹣2)
11.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A、B、E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )
A.(2,2)
B.(3,1)
C.(3,2)
D.(4,2)
12.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
A.﹣2a+3
B.﹣2a+1
C.﹣2a+2
D.﹣2a﹣2
二、填空题
13.在平面直角坐标系中,△ABO三个顶点的坐标分别为A(﹣2,4),B(﹣4,0),O(0,0).以原点O为位似中心,把这个三角形缩小为原来的,得到△CDO,则点A的对应点C的坐标是
.
14.如图,已知△ABO顶点A(﹣2,4),以原点O为位似中心,把△ABO缩小到原来的,则与点A对应的点A'的坐标是
.
15.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的,那么点B'的坐标是
.
16.如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是
.
17.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,则点B的横坐标是
.
18.如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第一象限内,将矩形OABC以原点O为位似中心放大为原来的2倍,得到矩形OA1B1C1,再将矩形OA1B1C1以原点O为位似中心放大2倍,得到矩形OA2B2C2…,以此类推,得到的矩形OAnBn?n的对角线交点的坐标为
.
三、解答题
19.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点的坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.
20.如图所示的平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣3,2),B(﹣1,3),C(﹣1,1),请按如下要求画图:
(1)以坐标原点O为旋转中心,将△ABC顺时针旋转90°,得到△A1B1C1,请画出△A1B1C1;
(2)以坐标原点O为位似中心,在x轴下方,画出△ABC的位似图形△A2B2C2,使它与△ABC的位似比为2:1.
21.如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(1,2),B(3,1)(每个方格的边长均为1个单位长度).
(1)将△OAB以点O为旋转中心,逆时针旋转90度得到△OA1B1,请画出△OA1B1;
(2)请以点O为位似中心,画出△OAB的位似三角形△OA2B2,使相似比为2:1.
22.如图,在直角坐标系中,△ABO三个顶点及点P的坐标分别是O(0,0),A(4,2),B(2,4),P(4,4),以点P为位似中心,画△DEF与△ABO位似,且相似比为1:2,请在网格中画出符合条件的△DEF.
参考答案
1.解:如图,
则点A′的坐标为(4,2)或(﹣4,﹣2).
故选:D.
2.解:∵△ABC与△DEF是位似图形,位似中心为O,OA:AD=3:4,
∴OA:OD=3:7,
∴S△ABC:S△DEF=9:49,
∵S△ABC=9,
∴△DEF的面积为:49.
故选:D.
3.解:∵△ABC是△DEF以点O为位似中心经过位似变换得到的,
∴AC∥FD,△ABC∽△DEF,
∵△ABC与△DEF的周长比为2:3,
∴=,
∵AC∥FD,
∴△AOC∽△DOF,
∴==,
故选:A.
4.解:∵四边形ABCD与四边形EFGH位似,其位似中心为点O,
∴==,
∵=,
∴==.
故选:A.
5.解:根据位似性质得出①△ABC与△DEF是位似图形,
②△ABC与△DEF是相似图形,且相似比是:=2,
③△ABC与△DEF的周长比等于相似比,即2:1,
④根据面积比等于相似比的平方,则△ABC与△DEF的面积比为4:1.
综上所述,正确的结论是:①③④.
故选:B.
6.解:根据位似的定义可得:△ABC与△DEF是位似图形,位似比是2:1,则周长的比是2:1,因而面积的比是4:1,故①②③正确,④错误.
故选:C.
7.解:∵点A的坐标为(﹣3,6),以原点O为位似中心,相似比为,把△ABO缩小,
∴点A的对应点A′的坐标为(﹣3×,6×)或(﹣3×(﹣),6×(﹣)),
即(﹣1,2)或(1,﹣2),
故选:B.
8.解:如图所示:P点即为所求,
故P点坐标为:(﹣3,2).
故选:C.
9.解:∵△ABC的顶点坐标分别为A(﹣4,2),B(﹣2,4),C(﹣4,4),以原点O为位似中心,
将△ABC缩小后得到△A′B′C′,点C的对应点C′的坐标为(2,﹣2),
∴点A的对应点A′的坐标为:(2,﹣1).
故选:B.
10.解:∵点A(7,5),B(4,3),先将线段AB向右平移1个单位,再向上平移1个单位,
∴点A,B平移后的对应点的坐标为A′(8,6),B(5,4),
∵以原点O为位似中心,将其缩小为原来的,得到线段CD,
∴则点A′的对应点C的坐标为:(4,3)或(﹣4,﹣3).
故选:B.
11.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,
∴=,==,
即=,=,
解得,OB=3,CD=2,
∴点C的坐标为(3,2),
故选:C.
12.解:设点B′的横坐标为x,
则B、C间的水平距离为a﹣1,B′、C间的水平距离为﹣x+1,
∵△ABC放大到原来的2倍得到△A′B′C,
∴2(a﹣1)=﹣x+1,
解得:x=﹣2a+3,
故选:A.
13.解:以原点O为位似中心,把这个三角形缩小为原来的,
则△ABO与△CDO的相似比为,
∵点A的坐标为(﹣2,4),
∴点C的坐标为(﹣2×,4×)或(2×,﹣4×),即(﹣1,2)或(1,﹣2),
故答案为:(﹣1,2)或(1,﹣2).
14.解:∵顶点A(﹣2,4),以原点O为位似中心,把△ABO缩小到原来的,
∴与点A对应的点A'的坐标是(﹣1,2)或(1,﹣2).
故答案为(﹣1,2)或(1,﹣2).
15.解:∵矩形OA'B'C'与矩形OABC关于点O位似,
∴矩形OA'B'C'∽矩形OABC,
∵矩形OA'B'C'的面积等于矩形OABC面积的,
∴矩形OA'B'C'与矩形OABC的相似比为,
∵点B的坐标为(﹣4,6),
∴点B'的坐标为(﹣4×,6×)或(4×,﹣6×),即(﹣2,3)或(2,﹣3),
故答案为:(﹣2,3)或(2,﹣3).
16.解:∵△DEF是由△ABC经过位似变换得到的,
∴△DEF∽△ABC,
∴S△DEF:S△ABC=()2,
∵D,E,F分别是OA,OB,OC的中点,
∴DE:AB=1:2,
∴S△DEF:S△ABC=1:4.
故答案为:1:4.
17.解:过点B、B'分别作BD⊥x轴于D,B'E⊥x轴于E,
∴∠BDC=∠B'EC=90°.
∵△ABC的位似图形是△A'B'C,
∴点B、C、B'在一条直线上,
∴∠BCD=∠B'CE,
∴△BCD∽△B'CE.
∴=,
又∵=,
∴=,
又∵点B'的横坐标是2,点C的坐标是(﹣1,0),
∴CE=3,
∴CD=.
∴OD=,
∴点B的横坐标为:﹣2.5.
故答案为:﹣2.5.
18.解:∵在第一象限内,将矩形AOCB以原点O为位似中心放大为原来的2倍,
∴矩形A1OC1B1与矩形AOCB是位似图形,点B与点B1是对应点,
∵OA=2,OC=1.
∵点B的坐标为(2,1),
∴点B1的坐标为(2×2,1×2),
∵将矩形A1OC1B1以原点O为位似中心放大2倍,得到矩形A2OC2B2…,
∴B2(2×2×2,1×2×2),
以此类推,Bn(2n+1,2n),
矩形OAnBn?n的对角线交点为Bn﹣1,即(2n,2n﹣1),
故答案为:(2n,2n﹣1).
19.解:(1)△A1B1C1如图所示C1(3,2)
(2)△A2B2C2如图所示C2(﹣6,4);
(3)∵D点的坐标为(a,b),
∴D2点的坐标为(2a,2b).
20.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
21.解:(1)如图所示,△OA1B1即为所求;
(2)如图所示,△OA2B2即为所求.
22.解:如图所示:
一、选择题
1.已知点A的坐标是(2,1),以坐标原点O为位似中心,像与原图形的位似比为2,则点A′的坐标为( )
A.()
B.(4,2)
C.(1,)或(﹣1,)
D.(4,2)或(﹣4,﹣2)
2.如图,△ABC与△DEF是位似图形,位似中心为O,OA:AD=3:4,S△ABC=9,则△DEF的面积为( )
A.12
B.16
C.21
D.49
3.如图,△ABC是△DEF以点O为位似中心经过位似变换得到的,若△ABC与△DEF的周长比为2:3,则OA与OD之比为( )
A.2:3
B.3:2
C.2:5
D.3:5
4.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且,则=( )
A.
B.
C.
D.
5.如图,D,E,F分别是OA,OB,OC的中点,下面的说法中:
①△ABC与△DEF是位似图形;
②△ABC与△DEF的相似比为1:2;
③△ABC与△DEF的周长之比为2:1;
④△ABC与△DEF的面积之比为4:1.
正确的是( )
A.①②③
B.①③④
C.①②④
D.②③④
6.如图,在△ABC外取一点O,连接AO、BO、CO,并分别取它们的中点D、E、F,得到△DEF,则下列说法:①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC与△DEF的周长比为2:1;④△ABC与△DEF的面积比为2:1,以上说法正确的个数是( )
A.1
B.2
C.3
D.4
7.如图,在平面直角坐标系中,已知点A(﹣3,6),B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(﹣1,2)
B.(﹣1,2)或(1,﹣2)
C.(﹣9,18)
D.(﹣9,18)或(9,﹣18)
8.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
A.(0,0)
B.(0,1)
C.(﹣3,2)
D.(3,﹣2)
9.如图,△ABC的顶点坐标分别为A(﹣4,2),B(﹣2,4),C(﹣4,4),以原点O为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,﹣2),则点A的对应点A′的坐标为( )
A.(2,﹣3)
B.(2,﹣1)
C.(3,﹣2)
D.(1,﹣2)
10.在平面直角坐标系中,已知两点A(7,5),B(4,3),先将线段AB向右平移1个单位,再向上平移1个单位,然后以原点O为位似中心,将其缩小为原来的,得到线段CD,则点A的对应点C的坐标为( )
A.(4,3)
B.(4,3)或(﹣4,﹣3)
C.(﹣4,﹣3)
D.(3,2)或(﹣3,﹣2)
11.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A、B、E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )
A.(2,2)
B.(3,1)
C.(3,2)
D.(4,2)
12.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
A.﹣2a+3
B.﹣2a+1
C.﹣2a+2
D.﹣2a﹣2
二、填空题
13.在平面直角坐标系中,△ABO三个顶点的坐标分别为A(﹣2,4),B(﹣4,0),O(0,0).以原点O为位似中心,把这个三角形缩小为原来的,得到△CDO,则点A的对应点C的坐标是
.
14.如图,已知△ABO顶点A(﹣2,4),以原点O为位似中心,把△ABO缩小到原来的,则与点A对应的点A'的坐标是
.
15.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的,那么点B'的坐标是
.
16.如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是
.
17.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,则点B的横坐标是
.
18.如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第一象限内,将矩形OABC以原点O为位似中心放大为原来的2倍,得到矩形OA1B1C1,再将矩形OA1B1C1以原点O为位似中心放大2倍,得到矩形OA2B2C2…,以此类推,得到的矩形OAnBn?n的对角线交点的坐标为
.
三、解答题
19.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点的坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.
20.如图所示的平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣3,2),B(﹣1,3),C(﹣1,1),请按如下要求画图:
(1)以坐标原点O为旋转中心,将△ABC顺时针旋转90°,得到△A1B1C1,请画出△A1B1C1;
(2)以坐标原点O为位似中心,在x轴下方,画出△ABC的位似图形△A2B2C2,使它与△ABC的位似比为2:1.
21.如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(1,2),B(3,1)(每个方格的边长均为1个单位长度).
(1)将△OAB以点O为旋转中心,逆时针旋转90度得到△OA1B1,请画出△OA1B1;
(2)请以点O为位似中心,画出△OAB的位似三角形△OA2B2,使相似比为2:1.
22.如图,在直角坐标系中,△ABO三个顶点及点P的坐标分别是O(0,0),A(4,2),B(2,4),P(4,4),以点P为位似中心,画△DEF与△ABO位似,且相似比为1:2,请在网格中画出符合条件的△DEF.
参考答案
1.解:如图,
则点A′的坐标为(4,2)或(﹣4,﹣2).
故选:D.
2.解:∵△ABC与△DEF是位似图形,位似中心为O,OA:AD=3:4,
∴OA:OD=3:7,
∴S△ABC:S△DEF=9:49,
∵S△ABC=9,
∴△DEF的面积为:49.
故选:D.
3.解:∵△ABC是△DEF以点O为位似中心经过位似变换得到的,
∴AC∥FD,△ABC∽△DEF,
∵△ABC与△DEF的周长比为2:3,
∴=,
∵AC∥FD,
∴△AOC∽△DOF,
∴==,
故选:A.
4.解:∵四边形ABCD与四边形EFGH位似,其位似中心为点O,
∴==,
∵=,
∴==.
故选:A.
5.解:根据位似性质得出①△ABC与△DEF是位似图形,
②△ABC与△DEF是相似图形,且相似比是:=2,
③△ABC与△DEF的周长比等于相似比,即2:1,
④根据面积比等于相似比的平方,则△ABC与△DEF的面积比为4:1.
综上所述,正确的结论是:①③④.
故选:B.
6.解:根据位似的定义可得:△ABC与△DEF是位似图形,位似比是2:1,则周长的比是2:1,因而面积的比是4:1,故①②③正确,④错误.
故选:C.
7.解:∵点A的坐标为(﹣3,6),以原点O为位似中心,相似比为,把△ABO缩小,
∴点A的对应点A′的坐标为(﹣3×,6×)或(﹣3×(﹣),6×(﹣)),
即(﹣1,2)或(1,﹣2),
故选:B.
8.解:如图所示:P点即为所求,
故P点坐标为:(﹣3,2).
故选:C.
9.解:∵△ABC的顶点坐标分别为A(﹣4,2),B(﹣2,4),C(﹣4,4),以原点O为位似中心,
将△ABC缩小后得到△A′B′C′,点C的对应点C′的坐标为(2,﹣2),
∴点A的对应点A′的坐标为:(2,﹣1).
故选:B.
10.解:∵点A(7,5),B(4,3),先将线段AB向右平移1个单位,再向上平移1个单位,
∴点A,B平移后的对应点的坐标为A′(8,6),B(5,4),
∵以原点O为位似中心,将其缩小为原来的,得到线段CD,
∴则点A′的对应点C的坐标为:(4,3)或(﹣4,﹣3).
故选:B.
11.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,
∴=,==,
即=,=,
解得,OB=3,CD=2,
∴点C的坐标为(3,2),
故选:C.
12.解:设点B′的横坐标为x,
则B、C间的水平距离为a﹣1,B′、C间的水平距离为﹣x+1,
∵△ABC放大到原来的2倍得到△A′B′C,
∴2(a﹣1)=﹣x+1,
解得:x=﹣2a+3,
故选:A.
13.解:以原点O为位似中心,把这个三角形缩小为原来的,
则△ABO与△CDO的相似比为,
∵点A的坐标为(﹣2,4),
∴点C的坐标为(﹣2×,4×)或(2×,﹣4×),即(﹣1,2)或(1,﹣2),
故答案为:(﹣1,2)或(1,﹣2).
14.解:∵顶点A(﹣2,4),以原点O为位似中心,把△ABO缩小到原来的,
∴与点A对应的点A'的坐标是(﹣1,2)或(1,﹣2).
故答案为(﹣1,2)或(1,﹣2).
15.解:∵矩形OA'B'C'与矩形OABC关于点O位似,
∴矩形OA'B'C'∽矩形OABC,
∵矩形OA'B'C'的面积等于矩形OABC面积的,
∴矩形OA'B'C'与矩形OABC的相似比为,
∵点B的坐标为(﹣4,6),
∴点B'的坐标为(﹣4×,6×)或(4×,﹣6×),即(﹣2,3)或(2,﹣3),
故答案为:(﹣2,3)或(2,﹣3).
16.解:∵△DEF是由△ABC经过位似变换得到的,
∴△DEF∽△ABC,
∴S△DEF:S△ABC=()2,
∵D,E,F分别是OA,OB,OC的中点,
∴DE:AB=1:2,
∴S△DEF:S△ABC=1:4.
故答案为:1:4.
17.解:过点B、B'分别作BD⊥x轴于D,B'E⊥x轴于E,
∴∠BDC=∠B'EC=90°.
∵△ABC的位似图形是△A'B'C,
∴点B、C、B'在一条直线上,
∴∠BCD=∠B'CE,
∴△BCD∽△B'CE.
∴=,
又∵=,
∴=,
又∵点B'的横坐标是2,点C的坐标是(﹣1,0),
∴CE=3,
∴CD=.
∴OD=,
∴点B的横坐标为:﹣2.5.
故答案为:﹣2.5.
18.解:∵在第一象限内,将矩形AOCB以原点O为位似中心放大为原来的2倍,
∴矩形A1OC1B1与矩形AOCB是位似图形,点B与点B1是对应点,
∵OA=2,OC=1.
∵点B的坐标为(2,1),
∴点B1的坐标为(2×2,1×2),
∵将矩形A1OC1B1以原点O为位似中心放大2倍,得到矩形A2OC2B2…,
∴B2(2×2×2,1×2×2),
以此类推,Bn(2n+1,2n),
矩形OAnBn?n的对角线交点为Bn﹣1,即(2n,2n﹣1),
故答案为:(2n,2n﹣1).
19.解:(1)△A1B1C1如图所示C1(3,2)
(2)△A2B2C2如图所示C2(﹣6,4);
(3)∵D点的坐标为(a,b),
∴D2点的坐标为(2a,2b).
20.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
21.解:(1)如图所示,△OA1B1即为所求;
(2)如图所示,△OA2B2即为所求.
22.解:如图所示:
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
