1.2怎样判定三角形相似 能力提升训练 2021-2022学年青岛版九年级数学上册(word版含答案)
文档属性
| 名称 | 1.2怎样判定三角形相似 能力提升训练 2021-2022学年青岛版九年级数学上册(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 535.3KB | ||
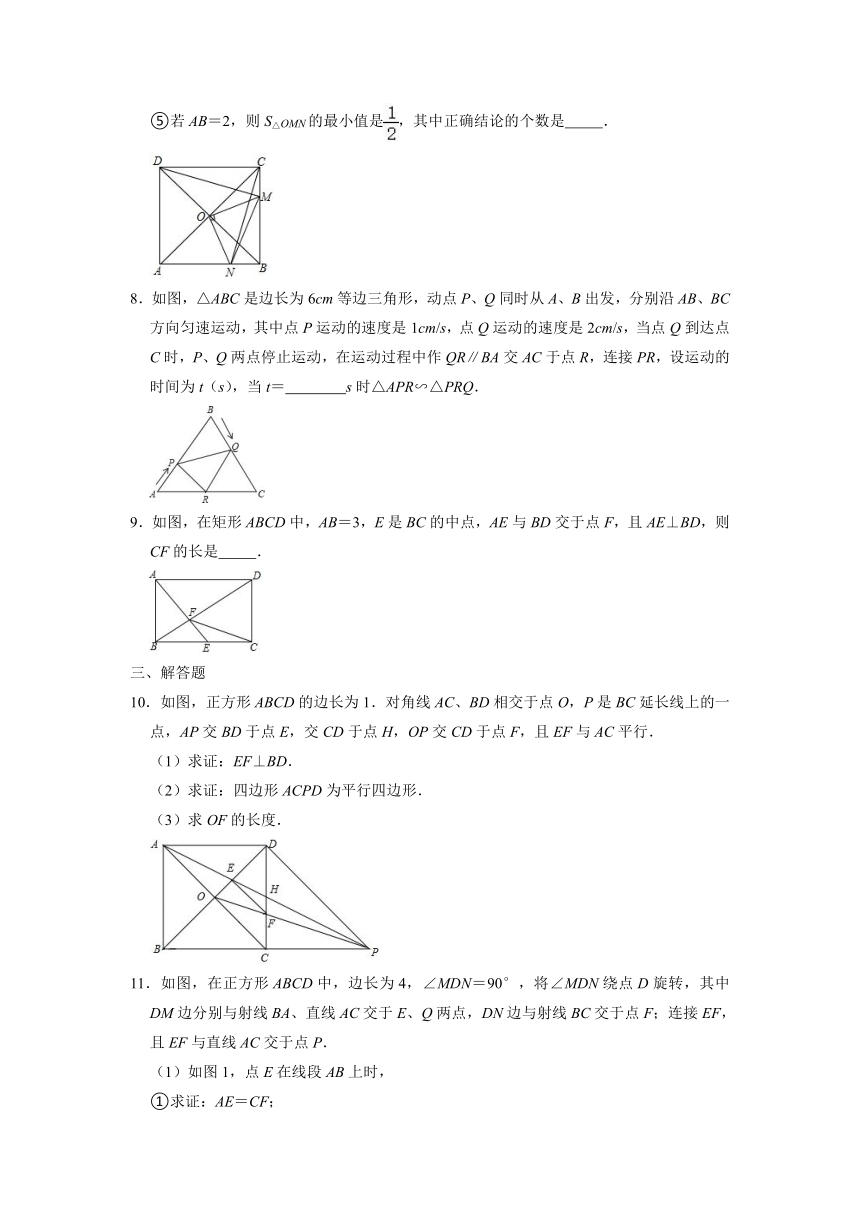
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 08:47:21 | ||
图片预览


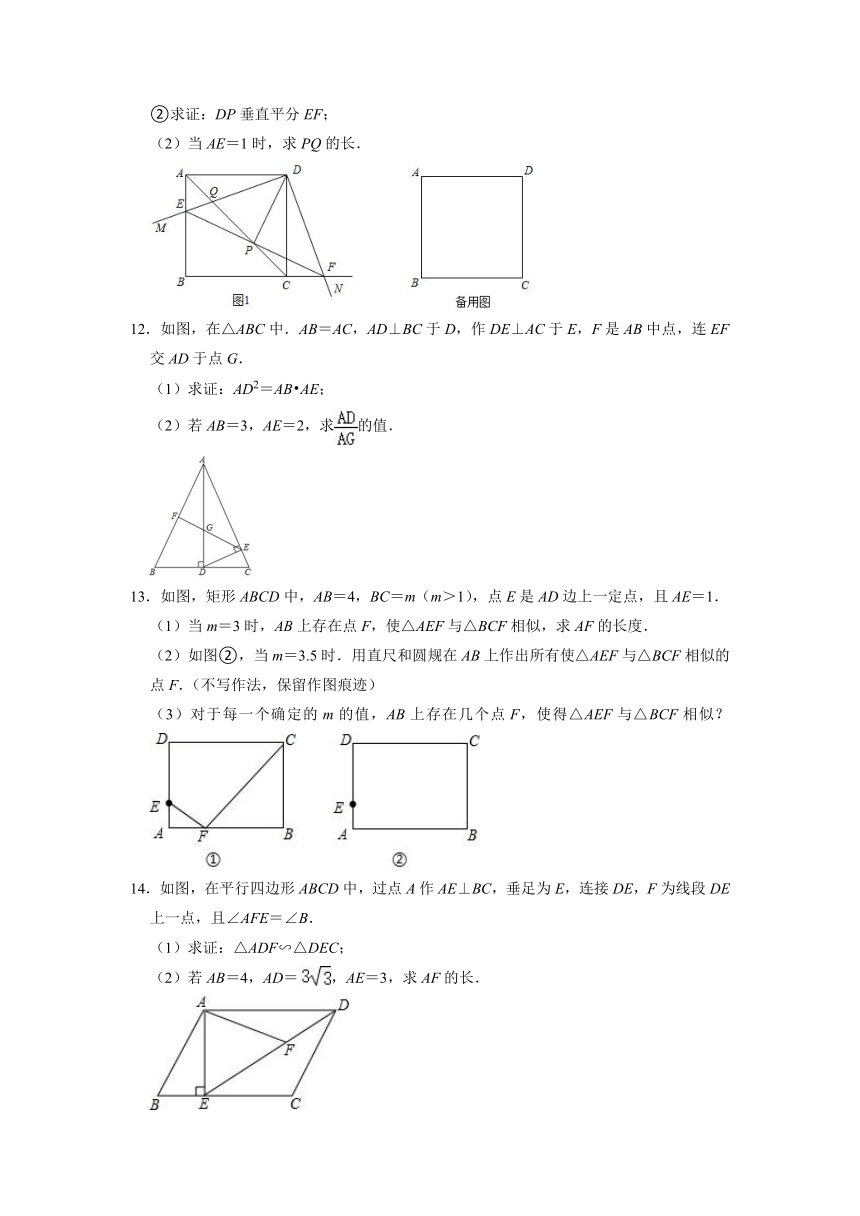
文档简介
2021-2022学年青岛版九年级数学上册《1.2怎样判定三角形相似》能力提升训练(附答案)
一、选择题
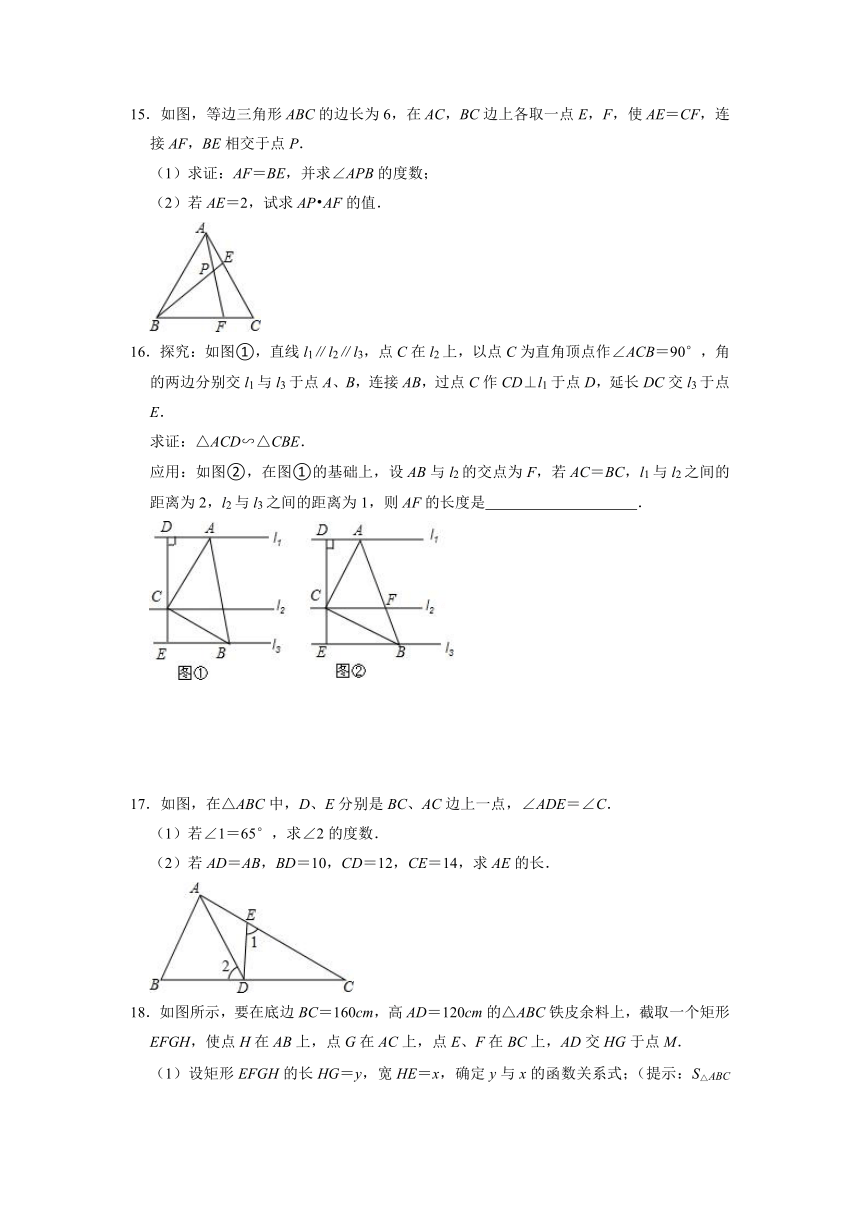
1.如图,在△ABC中,点E在BC边上,连接AE,点D在线段AE上,GD∥BA,且交BC于点G,DF∥BC,且交AC于点F,则下列结论一定正确的是( )
A.=
B.=
C.=
D.=
2.如图,正方形ABCD,点F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M,且交AD于点E,AC与DF交于点N,延长CB至G,使BG=BC,连接GM.有如下结论:①DE=AF;②AN=AB;③∠ADF=∠GMF;④S△ANF:S四边形CNFB=1:8.上述结论中,所有正确结论的序号是( )
A.①②
B.①③
C.①②③
D.②③④
3.如图,矩形ABCD,AD=1,CD=2,点P为边CD上的动点(P不与C重合),作点P关于BC的对称点Q,连接AP,BP和BQ,现有两个结论:①若DP≥1,当△APB为等腰三角形时,△APB和△PBQ一定相似;②记经过P,Q,A三点的圆面积为S,则4π≤S<.
下列说法正确的是( )
A.①对②对
B.①对②错
C.①错②对
D.①错②错
4.在矩形ABCD中,AB=6,AD=9,点E为线段AD上一点,且DE=2AE,点G是线段AB上的动点,EF⊥EG交BC所在直线于点F,连接GF.则GF的最小值是( )
A.3
B.6
C.6
D.3
5.如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M则下列结论①∠AME=90°;②∠BAF=∠EDB;③MD=2AM=4EM;④AM=MF,其中正确结论的个数是( )
A.4个
B.3个
C.2个
D.1个
6.如图,正方形ABCD中,AB=2,点N为AD为边上一点,连接BN,作AP⊥BN于点P,点M为AB边上一点,且∠PMA=∠PCB,连接CM.下列结论正确的个数有( )
(1)△PAM∽△PBC
(2)PM⊥PC;
(3)∠MPB=∠MCB;
(4)若点N为AD中点,则S△PCN=6
(5)AN=AM
A.5个
B.4个
C.3个
D.2个
二、填空题
7.如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是,其中正确结论的个数是
.
8.如图,△ABC是边长为6cm等边三角形,动点P、Q同时从A、B出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点停止运动,在运动过程中作QR∥BA交AC于点R,连接PR,设运动的时间为t(s),当t=
s时△APR∽△PRQ.
9.如图,在矩形ABCD中,AB=3,E是BC的中点,AE与BD交于点F,且AE⊥BD,则CF的长是
.
三、解答题
10.如图,正方形ABCD的边长为1.对角线AC、BD相交于点O,P是BC延长线上的一点,AP交BD于点E,交CD于点H,OP交CD于点F,且EF与AC平行.
(1)求证:EF⊥BD.
(2)求证:四边形ACPD为平行四边形.
(3)求OF的长度.
11.如图,在正方形ABCD中,边长为4,∠MDN=90°,将∠MDN绕点D旋转,其中DM边分别与射线BA、直线AC交于E、Q两点,DN边与射线BC交于点F;连接EF,且EF与直线AC交于点P.
(1)如图1,点E在线段AB上时,
①求证:AE=CF;
②求证:DP垂直平分EF;
(2)当AE=1时,求PQ的长.
12.如图,在△ABC中.AB=AC,AD⊥BC于D,作DE⊥AC于E,F是AB中点,连EF交AD于点G.
(1)求证:AD2=AB?AE;
(2)若AB=3,AE=2,求的值.
13.如图,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.
(1)当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
(2)如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)
(3)对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
14.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=,AE=3,求AF的长.
15.如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF,BE相交于点P.
(1)求证:AF=BE,并求∠APB的度数;
(2)若AE=2,试求AP?AF的值.
16.探究:如图①,直线l1∥l2∥l3,点C在l2上,以点C为直角顶点作∠ACB=90°,角的两边分别交l1与l3于点A、B,连接AB,过点C作CD⊥l1于点D,延长DC交l3于点E.
求证:△ACD∽△CBE.
应用:如图②,在图①的基础上,设AB与l2的交点为F,若AC=BC,l1与l2之间的距离为2,l2与l3之间的距离为1,则AF的长度是
.
17.如图,在△ABC中,D、E分别是BC、AC边上一点,∠ADE=∠C.
(1)若∠1=65°,求∠2的度数.
(2)若AD=AB,BD=10,CD=12,CE=14,求AE的长.
18.如图所示,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.
(1)设矩形EFGH的长HG=y,宽HE=x,确定y与x的函数关系式;(提示:S△ABC=S△AHG+S梯形BCGH)
(2)设矩形EFGH的面积为S,确定S与x的函数关系式;
(3)当x为何值时,矩形EFGH的面积S最大?
19.现有一块直角三角形木板,它的两条直角边分别为3米和4米.要把它加工成面积最大的正方形桌面,甲、乙二人加工方法分别如图1和图2所示.请运用所学知识说明谁的加工方法符合要求.
20.如图,在矩形ABCD中对角线AC、BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形,平行四边形对角线AE交BD、CD分别为点G和点H.
(1)证明:DG2=FG?BG;
(2)若AB=5,BC=6,则线段GH的长度.
21.如图,在梯形ABCD中,AD∥BC,∠BAD=90°,且对角线BD⊥DC,
试问:
①△ABD与△DCB相似吗?请说明理由;
②若AD=2,BC=8,请求出BD的长.
参考答案
1.解:∵DG∥AB,
∴=,故本选项不符合题意;
B、∵DF∥CE,
∴△ADF∽△AEC,
∴=≠,故本选项不符合题意;
C、∵DF∥CE,
∴△ADF∽△AEC,
∴=,
∵DG∥AB,
∴=,
∴=,故本选项符合题意;
D、∵DF∥CE,
∴=,
∵DG∥AB,
∴△DGE∽△ABE,
∴=,
∴≠,故本选项不符合题意;
故选:C.
2.解:∵四边形ABCD是正方形,
∴AD=AB=CD=BC,∠CDE=∠DAF=90°,
∵CE⊥DF,
∴∠DCE+∠CDF=∠ADF+∠CDF=90°,
∴∠ADF=∠DCE,
在△ADF与△DCE中,
,
∴△ADF≌△DCE(ASA),
∴DE=AF;故①正确;
∵AB∥CD,
∴=,
∵AF:FB=1:2,
∴AF:AB=AF:CD=1:3,
∴=,
∴=,
∵AC=AB,
∴=,
∴AN=AB;故②正确;
作GH⊥CE于H,设AF=DE=a,BF=2a,则AB=CD=BC=3a,EC=a,
由△CMD∽△CDE,可得CM=a,
由△GHC∽△CDE,可得CH=a,
∴CH=MH=CM,
∵GH⊥CM,
∴GM=GC,
∴∠GMH=∠GCH,
∵∠FMG+∠GMH=90°,∠DCE+∠GCM=90°,
∴∠FMG=∠DCE,
∵∠ADF=∠DCE,
∴∠ADF=∠GMF;故③正确,
(补充方法:延长MF交CG的延长线于T,证明CG=GT,利用直角三角形斜边中线的性质即可解决问题)
设△ANF的面积为m,
∵AF∥CD,
∴==,△AFN∽△CDN,
∴△ADN的面积为3m,△DCN的面积为9m,
∴△ADC的面积=△ABC的面积=12m,
∴S△ANF:S四边形CNFB=1:11,故④错误,
故选:C.
3.解:①如图1中,
∵DP≥1,当△APB为等腰三角形,
∴只有AP=AB,
在Rt△ADP中,∵∠D=90°,AP=2,AD=1,
∴PA=2AD,
∴∠APD=30°,
∵CD∥AB,
∴∠CPB=∠ABP,
∵AP=AB,
∴∠ABP=∠APB,
∴∠APB=∠CPB=75°,
∵P,Q关于BC对称,
∴BP=BQ,
∴∠BPC=∠BQC=75°,
∴△APB∽△BPQ,故①正确.
②当点O与B重合时,⊙O的半径最小,此时⊙O的面积为4π,
当点P与C重合时,设OA=OP=x,
在Rt△AOB中,则有x2=22+(x﹣1)2,
∴x=,
此时⊙O的面积=π,
观察图象可知:4π≤S<.故②正确,
故选:A.
4.解:如图,过点F作FM⊥AD于M,
∵四边形ABCD为矩形,
∴∠A=∠EMF=90°,MF=AB=6,
∵EF⊥GE,
∴∠AGE+∠AEG=90°,∠AEG+∠MEF=90°,
∴∠AGE=∠MEF,
∴△AEG∽△MFE,
∴=,
设AG=x,
∵AD=9,DE=2AE,
∴AE=3,
∴=,
∴ME=2x,
∴BF=AM=3+2x,
在Rt△GBF中,
GF2=GB2+BF2
=(6﹣x)2+(3+2x)2
=5x2+45,
∵点G在线段AB上,
∴0≤x≤6,
由二次函数的性质可知,当x=0时,GF2有最小值45,
∴GF的最小值为3,
故选:D.
5.解:(1)∵四边形ABCD为正方形,
∴AD=AB=∴BC,∠DAE=∠ABF=90°,
∵E、F分别为正方形ABCD的边AB,BC的中点,
∴AE=AB,BF=BC,
∴AE=BF,
∴△DAE≌△ABF(SAS),
∴∠BAF=∠ADE,
∵∠BAF+∠DAM=90°,
∴∠ADE+∠DAM=90°,
∴∠AME=∠ADE+∠DAM=90°,
故①正确;
(2)设AF与BD交于点N,正方形ABCD的边长为4,
则AE=BE=BF=2,
∴DE=AF==2,
∵AD∥BF,
∴△BFN∽△DAN,
∴==,
∴FN=,AN=,
∵S△AED=AD?AE=DE?AM,
∴AM===,
∴MN=AF﹣AM﹣NF=,
∴AM≠MN,
若∠BAF=∠EDB,
则∠ADE=∠EDB,
又∵DM=DM,∠DMA=∠DMN=90°,
∴△DAM≌△DNM(ASA),
∴AM=MN,
不符合题意,
故②错误;
(3)由(1)知,∠BAF=∠ADE,
又∵∠AME=∠EAD=∠AMD=90°,
∴△AME∽△DMA∽△DAE,
∴===,
∴AM=2EM,DM=2AM,
∴MD=2AM=4EM,
故③正确;
(4)由(2)知AM=,MN=,FN=,
∴MF=MN+FN=+=,
∴=,
故④正确;
故选:B.
6.解:(1)∵AP⊥BN,
∴∠PAM+∠PBA=90°,
∵∠PBA+∠PBC=90°,
∴∠PAM=∠PBC,
∵∠PMA=∠PCB,
∴△PAM∽△PBC,
故(1)正确;
(2)∵△PAM∽△PBC,
∴∠APM=∠BPC,
∴∠CPM=∠APB=90°,即PM⊥PC,
故(2)正确;
(3)∵∠MPC+∠MBC=90°+90°=180°,
∴B、C、P、M四点共圆,
∴∠MPB=∠MCB,
故(3)正确;
(4)过点P作EF⊥BC,分别交AD、BC于E、F点,
∵N为AD的中点,AB=2
∴AN=DN=,BC=EF=2,
∴BN=,
易证△ANP∽△NBA,得,
即,
∴PN=1,
∴PB=5﹣1=4,
∵AD∥BC,
∴△PEN∽△PFB,
∴,
∴PF=,
∴,
故(4)错误;
(5)易证△PAN∽△PAB,
∴,
∵△PAM∽△PBC,
∴,
∴,
∵AB=BC,
∴AM=AN,
故(5)正确;
故选:B.
7.解:∵正方形ABCD中,CD=BC,∠BCD=90°,
∴∠BCN+∠DCN=90°,
又∵CN⊥DM,
∴∠CDM+∠DCN=90°,
∴∠BCN=∠CDM,
又∵∠CBN=∠DCM=90°,
∴△CNB≌△DMC(ASA),故①正确;
根据△CNB≌△DMC,可得CM=BN,
又∵∠OCM=∠OBN=45°,OC=OB,
∴△OCM≌△OBN(SAS),
∴OM=ON,∠COM=∠BON,
∴∠DOC+∠COM=∠COB+∠BPN,即∠DOM=∠CON,
又∵DO=CO,
∴△CON≌△DOM(SAS),故②正确;
∵∠BON+∠BOM=∠COM+∠BOM=90°,
∴∠MON=90°,即△MON是等腰直角三角形,
又∵△AOD是等腰直角三角形,
∴△OMN∽△OAD,故③正确;
∵AB=BC,CM=BN,
∴BM=AN,
又∵Rt△BMN中,BM2+BN2=MN2,
∴AN2+CM2=MN2,故④正确;
∵△OCM≌△OBN,
∴四边形BMON的面积=△BOC的面积=1,即四边形BMON的面积是定值1,
∴当△MNB的面积最大时,△MNO的面积最小,
设BN=x=CM,则BM=2﹣x,
∴△MNB的面积=x(2﹣x)=﹣x2+x,
∴当x=1时,△MNB的面积有最大值,
此时S△OMN的最小值是1﹣=,故⑤正确;
综上所述,正确结论的个数是5个,
故答案为:5.
8.解:∵△ABC是边长为6cm等边三角形,
∴∠A=∠B=∠C=60°
∵QR∥BA
∴∠CRQ=∠A=60°,∠CQR=∠B=60°
∴△CRQ为等边三角形
∵点P运动的速度是1cm/s,点Q运动的速度是2cm/s
∴AP=t,PB=6﹣t,BQ=2t,CQ=CR=RQ=6﹣2t,AR=2t
∵QR∥BA
∴∠QRP=∠APR
若要△APR∽△PQR,则需满足∠RPQ=60°
∴∠BPQ+∠APR=120°,∠ARP+∠APR=120°
∴∠BPQ=∠ARP
又∵∠A=∠B
∴△APR∽△BQP
∴=
∴=
解得t=1.2
故答案为1.2.
9.解:延长AE、DC交于点G,
∵E是BC的中点,
∴BE=CE,
∵四边形ABCD为矩形,
∴AB∥CD,AB=CD,
∴∠ABE=∠GCE,
∵∠AEB=∠GEC,
∴△AEB≌△GEC(ASA),
∴AB=CG,
∴CD=CG,
即FC为△DFG的中线,
∵AE⊥BD,
CF=GD=CD=3,
故答案为3.
10.(1)证明:∵四边形ABCD是正方形,
∴AC⊥BD,
∵EF∥AC,
∴EF⊥BD;
(2)证明:
∵EF∥AC,
∴=,=,
∵四边形ABCD是正方形,
∴AD∥CP,OA=OC,
∴=,
即=,
∴AO∥DP,
∵AD∥CP,
∴四边形ACPD为平行四边形;
(3)解:由勾股定理得:AC=BD==,
∵四边形ACPD为平行四边形,
∴CP=AD=BC,
∴=,
∵AD∥BP,
∴==,
∴DE=BD=,OE=OD﹣DE=﹣=,
∵DO=BD=,
∵∠DEF=∠DOC=90°﹣∠EDF=45°,
∴∠DFE=45°,
∴EF=DE=,
在Rt△OEF中,由勾股定理得:OF===.
11.(1)①证明:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=∠DAE=∠DCF=90°,
∴∠ADC=∠MDN=90°,
∴∠ADE=∠CDF,
∴△ADE≌△CDF(ASA),
∴AE=CF.
②∵△ADE≌△CDF(ASA),
∴DE=DF,∵∠MDN=90°,
∴∠DEF=45°,
∵∠DAC=45°,
∴∠DAQ=∠PEQ,∵∠AQD=∠EQP,
∴△AQD∽△EQP,
∴=,
∴=,∵∠AQE=∠PQD,
∴△AQE∽△DQP,
∴∠QDP=∠QAE=45°,
∴∠DPE=90°,
∴DP⊥EF,∵DE=DF,
∴PE=PF,
∴DP垂直平分线段EF.
(2)解:①当点E在线段AB上时,作QH⊥AD于H,QG⊥AB于G.
在Rt△ADE中,DE==,
∵∠QAH=∠QAG=45°,
∴HQ=QG=AH=AG,设QH=x,
∵×4×x+×1×x=×1×4,
∵x=,
∴AQ=,DQ==,EQ=,
∵△AQD∽△EQP,
∴AQ?PQ=DQ?EQ,
∴PQ==.
②当点E在BA的延长线上时,作QH⊥AD于H,QG⊥AB于G.
在Rt△ADE中,DE==,
∵∠QAH=∠QAG=45°,
∴HQ=QG=AH=AG,设QH=x,
∵×4×x﹣×1×x=×1×4,
∵x=,
∴AQ=,DQ==,EQ=,
∵△AQD∽△EQP,
∴AQ?PQ=DQ?EQ,
∴PQ==.
综上所述,PQ的长为或.
12.(1)证明:∵AD⊥BC于D,作DE⊥AC于E,
∴∠ADC=∠AED=90°,
∵∠DAE=∠DAC,
∴△DAE∽△CAD,
∴=,
∴AD2=AC?AE,
∵AC=AB,
∴AD2=AB?AE.
解法二:可以直接证明△DAE∽△BAD,得出结论.
(2)解:如图,连接DF.
∵AB=3,∠ADB=90°,BF=AF,
∴DF=AB=,
∵AB=AC,AD⊥BC,
∴BD=DC,
∴DF∥AC,
∴===,
∴=.
13.解:(1)当∠AEF=∠BFC时,
要使△AEF∽△BFC,需=,即=,
解得AF=1或3;
当∠AEF=∠BCF时,
要使△AEF∽△BCF,需=,即=,
解得AF=1;
综上所述AF=1或3.
(3)当1<m<4且m≠3时,有3个;
当m=3时,有2个;
当m=4时,有2个;
当m>4时,有1个.
14.解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠B+∠C=180°,∠ADF=∠DEC,
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)∵AE⊥BC,AD=3,AE=3,
∴在Rt△DAE中,DE===6,
由(1)知△ADF∽△DEC,得=,
∴AF===2.
15.解:(1)∵△ABC为等边三角形,
∴AB=AC,∠C=∠CAB=60°,
在△ABE和△CAF中,,
∴△ABE≌△CAF,
∴AF=BE,∠ABE=∠CAF.
又∵∠APE=∠BPF=∠ABP+∠BAP,
∴∠APE=∠BAP+∠CAF=60°,
∴∠APB=180°﹣∠APE=120°
(2)∵∠C=∠APE=60°,∠PAE=∠CAF,
∴△APE∽△ACF,
∴=,即=,
∴AP?AF=12.
16.探究:证明:∵l1∥l3,CD⊥l1,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠DAC=90°,
∵∠ACB=90°,
∴∠ACD+∠ECB=90°,
∴∠DAC=∠ECB,
∴△ACD∽△CBE;
应用:在△ACD与△CBE中,
,
∴△ACD≌△BCE,
∴AD=CE=1,CD=BE=2,
∵∠ADC=CEB=90°,
∴AC=BC==,
∵∠ACB=90°,
∴AB=,
∵l1∥l2∥l3,
∴,
∴AF=.
故答案为:.
17.解:(1)∵∠1+∠EDC+∠C=180°,∠2+∠EDC+∠ADE=180°,且∠ADE=∠C,
∴∠2=∠1=65°;
(2)∵AD=AB,
∴∠B=∠2,
∵∠2=∠1,
∴∠B=∠1,
∵∠C=∠C,
∴△CBA∽△CED,
∴,
设AE=x,
则,
解得:x=,
即AE=.
18.解:(1)∵S△ABC=S△AHG+S梯形BCGH,
∴×160×120=y(120﹣x)+x(y+160),
化简得:y=﹣x+160;
(2)把y=﹣x+160代入S=xy,
得:S=﹣x2+160x;
(3)将S=﹣x2+160x,
右边配方得:S=﹣(x﹣60)2+4800;
∵﹣(x﹣60)2≤0,
∴当﹣(x﹣60)2=0时,即x=60时,S=﹣(x﹣60)2+4800有最大值4800.
19.解:图1加工的方法合理.
设图1加工桌面长xm,
∵FD∥BC,
∴Rt△AFD∽Rt△ACB,
∴AF:AC=FD:BC,
即(4﹣x):4=x:3,
解得x=,
设图2加工桌面长ym,过点C作CM⊥AB,垂足是M,与GF相交于点N,
∵GF∥DE,
∴△CGF∽△CAB,
∴CN:CM=GF:AB,
∴(CM﹣y):CM=y:AB.
∴AB=.
由面积相等可求得CM=2.4,
故此可求得y=;
很明显x>y,故x2>y2,
∴图1加工的方法合理.
20.解:(1)证明:∵ABCD是矩形,且AD∥BC,
∴△ADG∽△EBG.
∴=.
又∵△AGF∽△EGD,
∴=.
∴=.
∴DG2=FG?BG.
(2)∵ACED为平行四边形,AE,CD相交点H,
∴DH=DC=AB=.
∴在直角三角形ADH中,AH2=AD2+DH2
∴AH=.
又∵△ADG∽△EBG,
∴==.
∴AG=GE=×AE=×13=.
∴GH=AH﹣AG=﹣=.
21.解:①∵BD⊥DC(已知),
∴∠BDC=90°(垂直性质),
而∠BAD=90°(已知),
∴∠BDC=∠BAD(等量代换),
又∵AD∥BC(已知),
∴∠ADB=∠CBD(两直线平行,内错角相等).
∴△ABD∽△DCB(如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似).
②∵△ABD∽△DCB,
∴=,
而AD=2,BC=8,
∴=,
∴DB2=16,
∴BD=4.
一、选择题
1.如图,在△ABC中,点E在BC边上,连接AE,点D在线段AE上,GD∥BA,且交BC于点G,DF∥BC,且交AC于点F,则下列结论一定正确的是( )
A.=
B.=
C.=
D.=
2.如图,正方形ABCD,点F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M,且交AD于点E,AC与DF交于点N,延长CB至G,使BG=BC,连接GM.有如下结论:①DE=AF;②AN=AB;③∠ADF=∠GMF;④S△ANF:S四边形CNFB=1:8.上述结论中,所有正确结论的序号是( )
A.①②
B.①③
C.①②③
D.②③④
3.如图,矩形ABCD,AD=1,CD=2,点P为边CD上的动点(P不与C重合),作点P关于BC的对称点Q,连接AP,BP和BQ,现有两个结论:①若DP≥1,当△APB为等腰三角形时,△APB和△PBQ一定相似;②记经过P,Q,A三点的圆面积为S,则4π≤S<.
下列说法正确的是( )
A.①对②对
B.①对②错
C.①错②对
D.①错②错
4.在矩形ABCD中,AB=6,AD=9,点E为线段AD上一点,且DE=2AE,点G是线段AB上的动点,EF⊥EG交BC所在直线于点F,连接GF.则GF的最小值是( )
A.3
B.6
C.6
D.3
5.如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M则下列结论①∠AME=90°;②∠BAF=∠EDB;③MD=2AM=4EM;④AM=MF,其中正确结论的个数是( )
A.4个
B.3个
C.2个
D.1个
6.如图,正方形ABCD中,AB=2,点N为AD为边上一点,连接BN,作AP⊥BN于点P,点M为AB边上一点,且∠PMA=∠PCB,连接CM.下列结论正确的个数有( )
(1)△PAM∽△PBC
(2)PM⊥PC;
(3)∠MPB=∠MCB;
(4)若点N为AD中点,则S△PCN=6
(5)AN=AM
A.5个
B.4个
C.3个
D.2个
二、填空题
7.如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是,其中正确结论的个数是
.
8.如图,△ABC是边长为6cm等边三角形,动点P、Q同时从A、B出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点停止运动,在运动过程中作QR∥BA交AC于点R,连接PR,设运动的时间为t(s),当t=
s时△APR∽△PRQ.
9.如图,在矩形ABCD中,AB=3,E是BC的中点,AE与BD交于点F,且AE⊥BD,则CF的长是
.
三、解答题
10.如图,正方形ABCD的边长为1.对角线AC、BD相交于点O,P是BC延长线上的一点,AP交BD于点E,交CD于点H,OP交CD于点F,且EF与AC平行.
(1)求证:EF⊥BD.
(2)求证:四边形ACPD为平行四边形.
(3)求OF的长度.
11.如图,在正方形ABCD中,边长为4,∠MDN=90°,将∠MDN绕点D旋转,其中DM边分别与射线BA、直线AC交于E、Q两点,DN边与射线BC交于点F;连接EF,且EF与直线AC交于点P.
(1)如图1,点E在线段AB上时,
①求证:AE=CF;
②求证:DP垂直平分EF;
(2)当AE=1时,求PQ的长.
12.如图,在△ABC中.AB=AC,AD⊥BC于D,作DE⊥AC于E,F是AB中点,连EF交AD于点G.
(1)求证:AD2=AB?AE;
(2)若AB=3,AE=2,求的值.
13.如图,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.
(1)当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
(2)如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)
(3)对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
14.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=,AE=3,求AF的长.
15.如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF,BE相交于点P.
(1)求证:AF=BE,并求∠APB的度数;
(2)若AE=2,试求AP?AF的值.
16.探究:如图①,直线l1∥l2∥l3,点C在l2上,以点C为直角顶点作∠ACB=90°,角的两边分别交l1与l3于点A、B,连接AB,过点C作CD⊥l1于点D,延长DC交l3于点E.
求证:△ACD∽△CBE.
应用:如图②,在图①的基础上,设AB与l2的交点为F,若AC=BC,l1与l2之间的距离为2,l2与l3之间的距离为1,则AF的长度是
.
17.如图,在△ABC中,D、E分别是BC、AC边上一点,∠ADE=∠C.
(1)若∠1=65°,求∠2的度数.
(2)若AD=AB,BD=10,CD=12,CE=14,求AE的长.
18.如图所示,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.
(1)设矩形EFGH的长HG=y,宽HE=x,确定y与x的函数关系式;(提示:S△ABC=S△AHG+S梯形BCGH)
(2)设矩形EFGH的面积为S,确定S与x的函数关系式;
(3)当x为何值时,矩形EFGH的面积S最大?
19.现有一块直角三角形木板,它的两条直角边分别为3米和4米.要把它加工成面积最大的正方形桌面,甲、乙二人加工方法分别如图1和图2所示.请运用所学知识说明谁的加工方法符合要求.
20.如图,在矩形ABCD中对角线AC、BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形,平行四边形对角线AE交BD、CD分别为点G和点H.
(1)证明:DG2=FG?BG;
(2)若AB=5,BC=6,则线段GH的长度.
21.如图,在梯形ABCD中,AD∥BC,∠BAD=90°,且对角线BD⊥DC,
试问:
①△ABD与△DCB相似吗?请说明理由;
②若AD=2,BC=8,请求出BD的长.
参考答案
1.解:∵DG∥AB,
∴=,故本选项不符合题意;
B、∵DF∥CE,
∴△ADF∽△AEC,
∴=≠,故本选项不符合题意;
C、∵DF∥CE,
∴△ADF∽△AEC,
∴=,
∵DG∥AB,
∴=,
∴=,故本选项符合题意;
D、∵DF∥CE,
∴=,
∵DG∥AB,
∴△DGE∽△ABE,
∴=,
∴≠,故本选项不符合题意;
故选:C.
2.解:∵四边形ABCD是正方形,
∴AD=AB=CD=BC,∠CDE=∠DAF=90°,
∵CE⊥DF,
∴∠DCE+∠CDF=∠ADF+∠CDF=90°,
∴∠ADF=∠DCE,
在△ADF与△DCE中,
,
∴△ADF≌△DCE(ASA),
∴DE=AF;故①正确;
∵AB∥CD,
∴=,
∵AF:FB=1:2,
∴AF:AB=AF:CD=1:3,
∴=,
∴=,
∵AC=AB,
∴=,
∴AN=AB;故②正确;
作GH⊥CE于H,设AF=DE=a,BF=2a,则AB=CD=BC=3a,EC=a,
由△CMD∽△CDE,可得CM=a,
由△GHC∽△CDE,可得CH=a,
∴CH=MH=CM,
∵GH⊥CM,
∴GM=GC,
∴∠GMH=∠GCH,
∵∠FMG+∠GMH=90°,∠DCE+∠GCM=90°,
∴∠FMG=∠DCE,
∵∠ADF=∠DCE,
∴∠ADF=∠GMF;故③正确,
(补充方法:延长MF交CG的延长线于T,证明CG=GT,利用直角三角形斜边中线的性质即可解决问题)
设△ANF的面积为m,
∵AF∥CD,
∴==,△AFN∽△CDN,
∴△ADN的面积为3m,△DCN的面积为9m,
∴△ADC的面积=△ABC的面积=12m,
∴S△ANF:S四边形CNFB=1:11,故④错误,
故选:C.
3.解:①如图1中,
∵DP≥1,当△APB为等腰三角形,
∴只有AP=AB,
在Rt△ADP中,∵∠D=90°,AP=2,AD=1,
∴PA=2AD,
∴∠APD=30°,
∵CD∥AB,
∴∠CPB=∠ABP,
∵AP=AB,
∴∠ABP=∠APB,
∴∠APB=∠CPB=75°,
∵P,Q关于BC对称,
∴BP=BQ,
∴∠BPC=∠BQC=75°,
∴△APB∽△BPQ,故①正确.
②当点O与B重合时,⊙O的半径最小,此时⊙O的面积为4π,
当点P与C重合时,设OA=OP=x,
在Rt△AOB中,则有x2=22+(x﹣1)2,
∴x=,
此时⊙O的面积=π,
观察图象可知:4π≤S<.故②正确,
故选:A.
4.解:如图,过点F作FM⊥AD于M,
∵四边形ABCD为矩形,
∴∠A=∠EMF=90°,MF=AB=6,
∵EF⊥GE,
∴∠AGE+∠AEG=90°,∠AEG+∠MEF=90°,
∴∠AGE=∠MEF,
∴△AEG∽△MFE,
∴=,
设AG=x,
∵AD=9,DE=2AE,
∴AE=3,
∴=,
∴ME=2x,
∴BF=AM=3+2x,
在Rt△GBF中,
GF2=GB2+BF2
=(6﹣x)2+(3+2x)2
=5x2+45,
∵点G在线段AB上,
∴0≤x≤6,
由二次函数的性质可知,当x=0时,GF2有最小值45,
∴GF的最小值为3,
故选:D.
5.解:(1)∵四边形ABCD为正方形,
∴AD=AB=∴BC,∠DAE=∠ABF=90°,
∵E、F分别为正方形ABCD的边AB,BC的中点,
∴AE=AB,BF=BC,
∴AE=BF,
∴△DAE≌△ABF(SAS),
∴∠BAF=∠ADE,
∵∠BAF+∠DAM=90°,
∴∠ADE+∠DAM=90°,
∴∠AME=∠ADE+∠DAM=90°,
故①正确;
(2)设AF与BD交于点N,正方形ABCD的边长为4,
则AE=BE=BF=2,
∴DE=AF==2,
∵AD∥BF,
∴△BFN∽△DAN,
∴==,
∴FN=,AN=,
∵S△AED=AD?AE=DE?AM,
∴AM===,
∴MN=AF﹣AM﹣NF=,
∴AM≠MN,
若∠BAF=∠EDB,
则∠ADE=∠EDB,
又∵DM=DM,∠DMA=∠DMN=90°,
∴△DAM≌△DNM(ASA),
∴AM=MN,
不符合题意,
故②错误;
(3)由(1)知,∠BAF=∠ADE,
又∵∠AME=∠EAD=∠AMD=90°,
∴△AME∽△DMA∽△DAE,
∴===,
∴AM=2EM,DM=2AM,
∴MD=2AM=4EM,
故③正确;
(4)由(2)知AM=,MN=,FN=,
∴MF=MN+FN=+=,
∴=,
故④正确;
故选:B.
6.解:(1)∵AP⊥BN,
∴∠PAM+∠PBA=90°,
∵∠PBA+∠PBC=90°,
∴∠PAM=∠PBC,
∵∠PMA=∠PCB,
∴△PAM∽△PBC,
故(1)正确;
(2)∵△PAM∽△PBC,
∴∠APM=∠BPC,
∴∠CPM=∠APB=90°,即PM⊥PC,
故(2)正确;
(3)∵∠MPC+∠MBC=90°+90°=180°,
∴B、C、P、M四点共圆,
∴∠MPB=∠MCB,
故(3)正确;
(4)过点P作EF⊥BC,分别交AD、BC于E、F点,
∵N为AD的中点,AB=2
∴AN=DN=,BC=EF=2,
∴BN=,
易证△ANP∽△NBA,得,
即,
∴PN=1,
∴PB=5﹣1=4,
∵AD∥BC,
∴△PEN∽△PFB,
∴,
∴PF=,
∴,
故(4)错误;
(5)易证△PAN∽△PAB,
∴,
∵△PAM∽△PBC,
∴,
∴,
∵AB=BC,
∴AM=AN,
故(5)正确;
故选:B.
7.解:∵正方形ABCD中,CD=BC,∠BCD=90°,
∴∠BCN+∠DCN=90°,
又∵CN⊥DM,
∴∠CDM+∠DCN=90°,
∴∠BCN=∠CDM,
又∵∠CBN=∠DCM=90°,
∴△CNB≌△DMC(ASA),故①正确;
根据△CNB≌△DMC,可得CM=BN,
又∵∠OCM=∠OBN=45°,OC=OB,
∴△OCM≌△OBN(SAS),
∴OM=ON,∠COM=∠BON,
∴∠DOC+∠COM=∠COB+∠BPN,即∠DOM=∠CON,
又∵DO=CO,
∴△CON≌△DOM(SAS),故②正确;
∵∠BON+∠BOM=∠COM+∠BOM=90°,
∴∠MON=90°,即△MON是等腰直角三角形,
又∵△AOD是等腰直角三角形,
∴△OMN∽△OAD,故③正确;
∵AB=BC,CM=BN,
∴BM=AN,
又∵Rt△BMN中,BM2+BN2=MN2,
∴AN2+CM2=MN2,故④正确;
∵△OCM≌△OBN,
∴四边形BMON的面积=△BOC的面积=1,即四边形BMON的面积是定值1,
∴当△MNB的面积最大时,△MNO的面积最小,
设BN=x=CM,则BM=2﹣x,
∴△MNB的面积=x(2﹣x)=﹣x2+x,
∴当x=1时,△MNB的面积有最大值,
此时S△OMN的最小值是1﹣=,故⑤正确;
综上所述,正确结论的个数是5个,
故答案为:5.
8.解:∵△ABC是边长为6cm等边三角形,
∴∠A=∠B=∠C=60°
∵QR∥BA
∴∠CRQ=∠A=60°,∠CQR=∠B=60°
∴△CRQ为等边三角形
∵点P运动的速度是1cm/s,点Q运动的速度是2cm/s
∴AP=t,PB=6﹣t,BQ=2t,CQ=CR=RQ=6﹣2t,AR=2t
∵QR∥BA
∴∠QRP=∠APR
若要△APR∽△PQR,则需满足∠RPQ=60°
∴∠BPQ+∠APR=120°,∠ARP+∠APR=120°
∴∠BPQ=∠ARP
又∵∠A=∠B
∴△APR∽△BQP
∴=
∴=
解得t=1.2
故答案为1.2.
9.解:延长AE、DC交于点G,
∵E是BC的中点,
∴BE=CE,
∵四边形ABCD为矩形,
∴AB∥CD,AB=CD,
∴∠ABE=∠GCE,
∵∠AEB=∠GEC,
∴△AEB≌△GEC(ASA),
∴AB=CG,
∴CD=CG,
即FC为△DFG的中线,
∵AE⊥BD,
CF=GD=CD=3,
故答案为3.
10.(1)证明:∵四边形ABCD是正方形,
∴AC⊥BD,
∵EF∥AC,
∴EF⊥BD;
(2)证明:
∵EF∥AC,
∴=,=,
∵四边形ABCD是正方形,
∴AD∥CP,OA=OC,
∴=,
即=,
∴AO∥DP,
∵AD∥CP,
∴四边形ACPD为平行四边形;
(3)解:由勾股定理得:AC=BD==,
∵四边形ACPD为平行四边形,
∴CP=AD=BC,
∴=,
∵AD∥BP,
∴==,
∴DE=BD=,OE=OD﹣DE=﹣=,
∵DO=BD=,
∵∠DEF=∠DOC=90°﹣∠EDF=45°,
∴∠DFE=45°,
∴EF=DE=,
在Rt△OEF中,由勾股定理得:OF===.
11.(1)①证明:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=∠DAE=∠DCF=90°,
∴∠ADC=∠MDN=90°,
∴∠ADE=∠CDF,
∴△ADE≌△CDF(ASA),
∴AE=CF.
②∵△ADE≌△CDF(ASA),
∴DE=DF,∵∠MDN=90°,
∴∠DEF=45°,
∵∠DAC=45°,
∴∠DAQ=∠PEQ,∵∠AQD=∠EQP,
∴△AQD∽△EQP,
∴=,
∴=,∵∠AQE=∠PQD,
∴△AQE∽△DQP,
∴∠QDP=∠QAE=45°,
∴∠DPE=90°,
∴DP⊥EF,∵DE=DF,
∴PE=PF,
∴DP垂直平分线段EF.
(2)解:①当点E在线段AB上时,作QH⊥AD于H,QG⊥AB于G.
在Rt△ADE中,DE==,
∵∠QAH=∠QAG=45°,
∴HQ=QG=AH=AG,设QH=x,
∵×4×x+×1×x=×1×4,
∵x=,
∴AQ=,DQ==,EQ=,
∵△AQD∽△EQP,
∴AQ?PQ=DQ?EQ,
∴PQ==.
②当点E在BA的延长线上时,作QH⊥AD于H,QG⊥AB于G.
在Rt△ADE中,DE==,
∵∠QAH=∠QAG=45°,
∴HQ=QG=AH=AG,设QH=x,
∵×4×x﹣×1×x=×1×4,
∵x=,
∴AQ=,DQ==,EQ=,
∵△AQD∽△EQP,
∴AQ?PQ=DQ?EQ,
∴PQ==.
综上所述,PQ的长为或.
12.(1)证明:∵AD⊥BC于D,作DE⊥AC于E,
∴∠ADC=∠AED=90°,
∵∠DAE=∠DAC,
∴△DAE∽△CAD,
∴=,
∴AD2=AC?AE,
∵AC=AB,
∴AD2=AB?AE.
解法二:可以直接证明△DAE∽△BAD,得出结论.
(2)解:如图,连接DF.
∵AB=3,∠ADB=90°,BF=AF,
∴DF=AB=,
∵AB=AC,AD⊥BC,
∴BD=DC,
∴DF∥AC,
∴===,
∴=.
13.解:(1)当∠AEF=∠BFC时,
要使△AEF∽△BFC,需=,即=,
解得AF=1或3;
当∠AEF=∠BCF时,
要使△AEF∽△BCF,需=,即=,
解得AF=1;
综上所述AF=1或3.
(3)当1<m<4且m≠3时,有3个;
当m=3时,有2个;
当m=4时,有2个;
当m>4时,有1个.
14.解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠B+∠C=180°,∠ADF=∠DEC,
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)∵AE⊥BC,AD=3,AE=3,
∴在Rt△DAE中,DE===6,
由(1)知△ADF∽△DEC,得=,
∴AF===2.
15.解:(1)∵△ABC为等边三角形,
∴AB=AC,∠C=∠CAB=60°,
在△ABE和△CAF中,,
∴△ABE≌△CAF,
∴AF=BE,∠ABE=∠CAF.
又∵∠APE=∠BPF=∠ABP+∠BAP,
∴∠APE=∠BAP+∠CAF=60°,
∴∠APB=180°﹣∠APE=120°
(2)∵∠C=∠APE=60°,∠PAE=∠CAF,
∴△APE∽△ACF,
∴=,即=,
∴AP?AF=12.
16.探究:证明:∵l1∥l3,CD⊥l1,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠DAC=90°,
∵∠ACB=90°,
∴∠ACD+∠ECB=90°,
∴∠DAC=∠ECB,
∴△ACD∽△CBE;
应用:在△ACD与△CBE中,
,
∴△ACD≌△BCE,
∴AD=CE=1,CD=BE=2,
∵∠ADC=CEB=90°,
∴AC=BC==,
∵∠ACB=90°,
∴AB=,
∵l1∥l2∥l3,
∴,
∴AF=.
故答案为:.
17.解:(1)∵∠1+∠EDC+∠C=180°,∠2+∠EDC+∠ADE=180°,且∠ADE=∠C,
∴∠2=∠1=65°;
(2)∵AD=AB,
∴∠B=∠2,
∵∠2=∠1,
∴∠B=∠1,
∵∠C=∠C,
∴△CBA∽△CED,
∴,
设AE=x,
则,
解得:x=,
即AE=.
18.解:(1)∵S△ABC=S△AHG+S梯形BCGH,
∴×160×120=y(120﹣x)+x(y+160),
化简得:y=﹣x+160;
(2)把y=﹣x+160代入S=xy,
得:S=﹣x2+160x;
(3)将S=﹣x2+160x,
右边配方得:S=﹣(x﹣60)2+4800;
∵﹣(x﹣60)2≤0,
∴当﹣(x﹣60)2=0时,即x=60时,S=﹣(x﹣60)2+4800有最大值4800.
19.解:图1加工的方法合理.
设图1加工桌面长xm,
∵FD∥BC,
∴Rt△AFD∽Rt△ACB,
∴AF:AC=FD:BC,
即(4﹣x):4=x:3,
解得x=,
设图2加工桌面长ym,过点C作CM⊥AB,垂足是M,与GF相交于点N,
∵GF∥DE,
∴△CGF∽△CAB,
∴CN:CM=GF:AB,
∴(CM﹣y):CM=y:AB.
∴AB=.
由面积相等可求得CM=2.4,
故此可求得y=;
很明显x>y,故x2>y2,
∴图1加工的方法合理.
20.解:(1)证明:∵ABCD是矩形,且AD∥BC,
∴△ADG∽△EBG.
∴=.
又∵△AGF∽△EGD,
∴=.
∴=.
∴DG2=FG?BG.
(2)∵ACED为平行四边形,AE,CD相交点H,
∴DH=DC=AB=.
∴在直角三角形ADH中,AH2=AD2+DH2
∴AH=.
又∵△ADG∽△EBG,
∴==.
∴AG=GE=×AE=×13=.
∴GH=AH﹣AG=﹣=.
21.解:①∵BD⊥DC(已知),
∴∠BDC=90°(垂直性质),
而∠BAD=90°(已知),
∴∠BDC=∠BAD(等量代换),
又∵AD∥BC(已知),
∴∠ADB=∠CBD(两直线平行,内错角相等).
∴△ABD∽△DCB(如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似).
②∵△ABD∽△DCB,
∴=,
而AD=2,BC=8,
∴=,
∴DB2=16,
∴BD=4.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
