2021-2022学年鲁教版(五四制)六年级数学上册第一章丰富的图形世界课后提高练习(Word版,含答案解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)六年级数学上册第一章丰富的图形世界课后提高练习(Word版,含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 216.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 00:00:00 | ||
图片预览

文档简介
2021-2022学年鲁教版六年级数学上册《第1章丰富的图形世界》课后提高练习(附答案)
一、选择题
1.下面四个几何体的三视图中没有矩形的是( )
A.
B.
C.
D.
2.如图,是某几何体的展开图,AD=16π,则r=( )
A.2
B.4
C.8
D.16
4.从左面观察如图所示的几何体,看到的平面图形是( )
A.
B.
C.
D.
5.如图,由七个相同的小正方体拼成立体图形,若从标有①②③④的四个小正方体中取走一个或多个后,余下的几何体与原几何体的左视图相同,则取走的正方体不可能是( )
A.④
B.③
C.②
D.①
6.由几个大小相同的小正方体搭建而成的几何体的主视图和俯视图如图所示,则搭建这个几何体所需要的小正方体的个数至少为( )
A.5
B.6
C.7
D.8
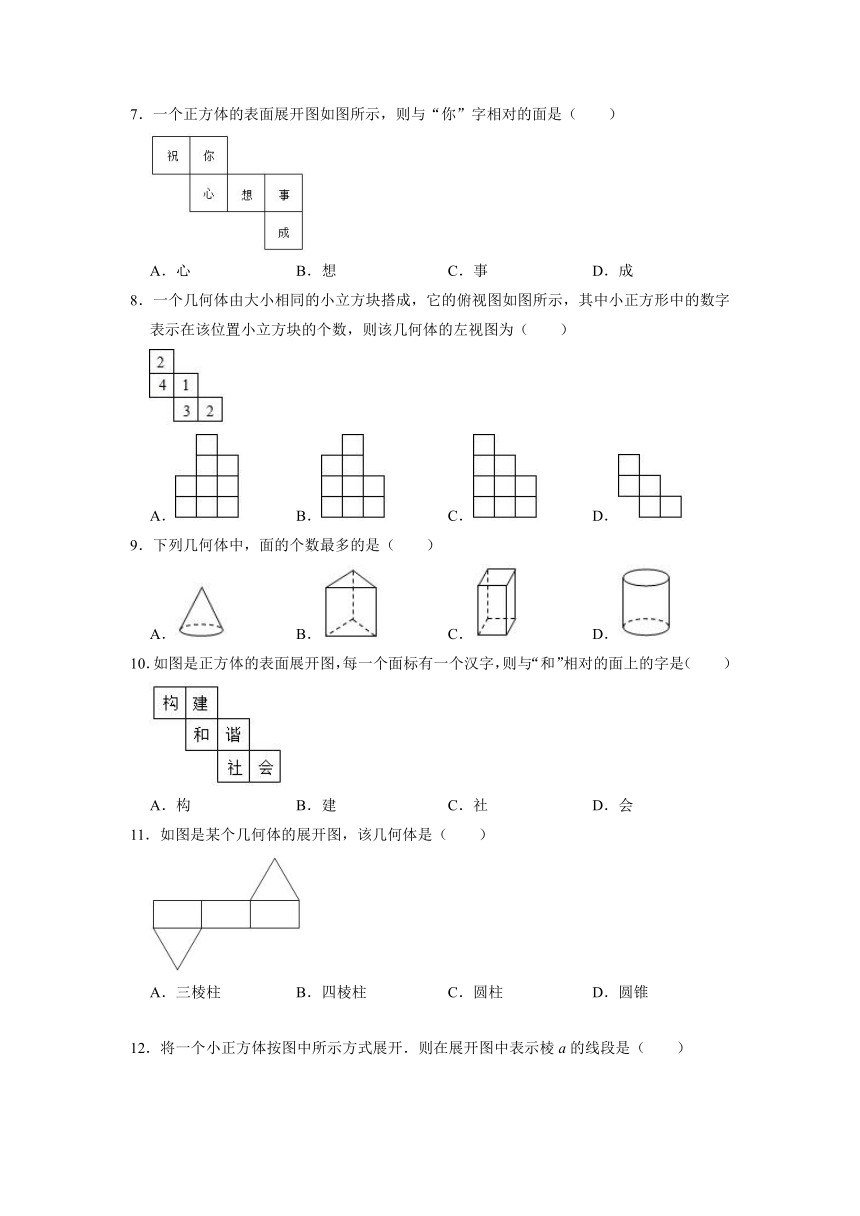
7.一个正方体的表面展开图如图所示,则与“你”字相对的面是( )
A.心
B.想
C.事
D.成
8.一个几何体由大小相同的小立方块搭成,它的俯视图如图所示,其中小正方形中的数字表示在该位置小立方块的个数,则该几何体的左视图为( )
A.
B.
C.
D.
9.下列几何体中,面的个数最多的是( )
A.
B.
C.
D.
10.如图是正方体的表面展开图,每一个面标有一个汉字,则与“和”相对的面上的字是( )
A.构
B.建
C.社
D.会
11.如图是某个几何体的展开图,该几何体是( )
A.三棱柱
B.四棱柱
C.圆柱
D.圆锥
12.将一个小正方体按图中所示方式展开.则在展开图中表示棱a的线段是( )
A.AB
B.CD
C.DE
D.CF
13.图1是一个小正方体的展开图,小正方体从图2的所示位置依次翻到第1格,第2格,第3格,这时小正方体朝上一面的字是( )
A.常
B.州
C.越
D.来
14.下列图形绕虚线旋转一周,便能形成圆锥体的是( )
A.
B.
C.
D.
15.用一平面截一个正方体,不能得到的截面形状是( )
A.等边三角形
B.长方形
C.六边形
D.七边形
16.如图所示是正方体的展开图,原正方体“4”的相邻面上的数字之和是( )
A.2
B.12
C.14
D.15
17.下列图形中不能作为正方体的展开图的是( )
A.B.C.D.
18.用一个平面去截正方体,截面图形不可能是( )
A.
B.
C.
D.
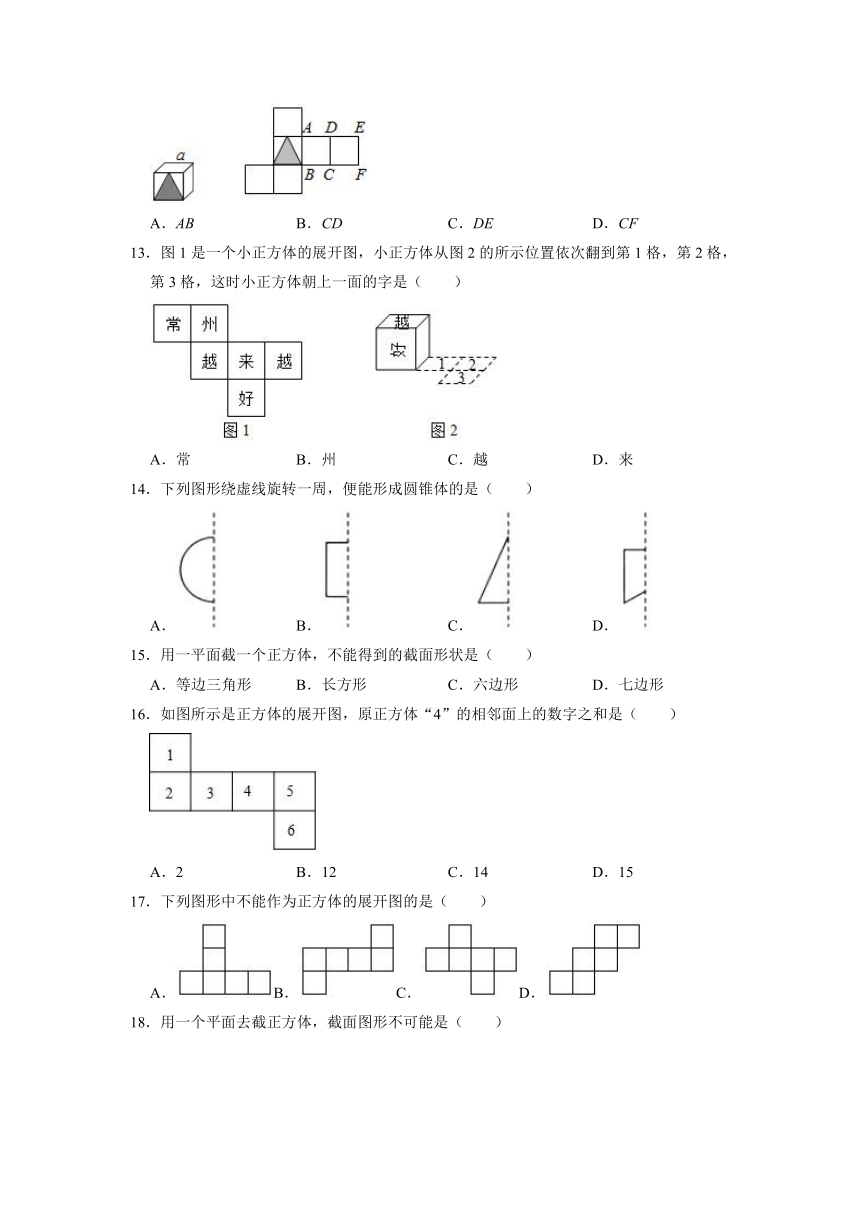
19.如图形状的四张纸板,按图中线经过折叠可以围成一个直三棱柱的是( )
A.
B.
C.
D.
二、填空题
20.一个由125个同样的小正方体组成的大正方体,从这个大正方体中抽出若干个正方体,把大正方体中相对的两面打通,结果如图,则图中剩下的小正方有
个.
21.如图是一个正方体纸盒的展开图,当折成纸盒时,与数11重合的数是
.
22.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是
.
23.流星划过天空时留下一道明亮的光线,用数学知识解释为
.
24.如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是
.
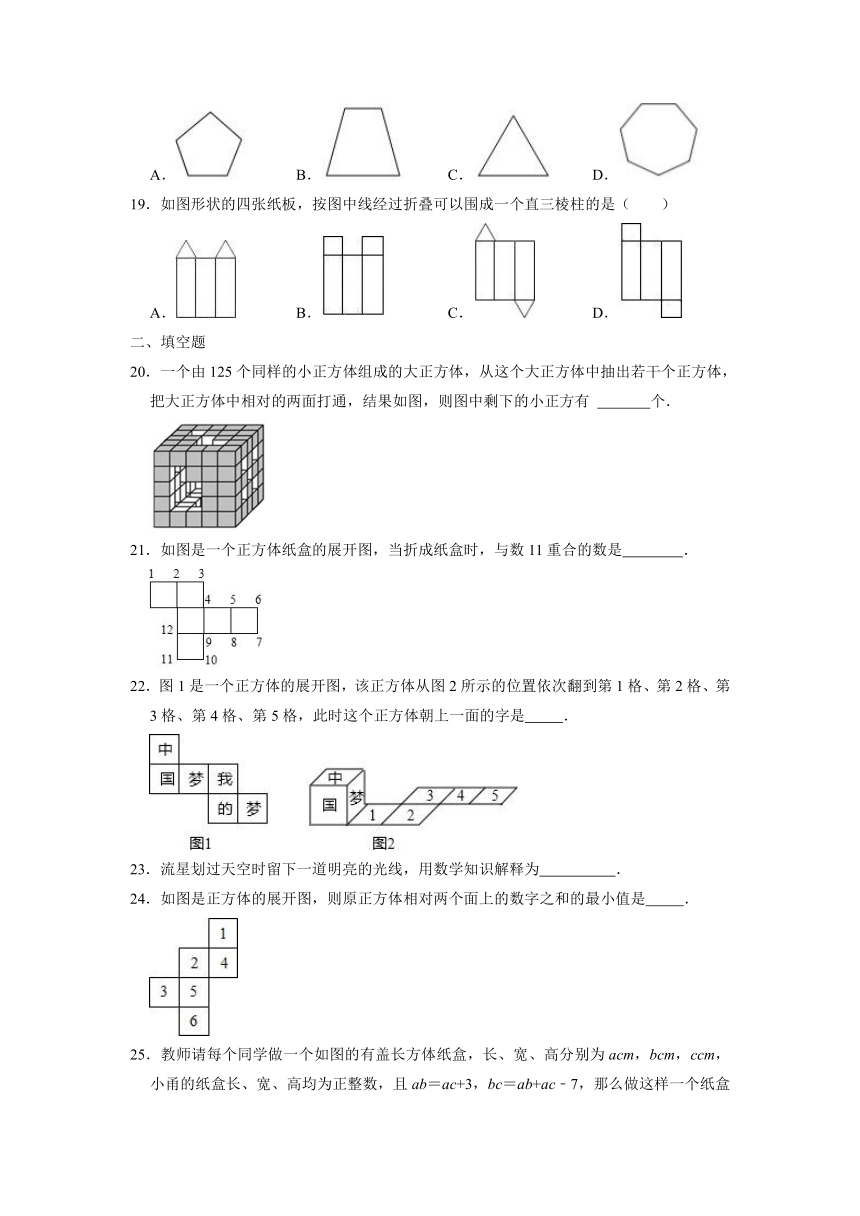
25.教师请每个同学做一个如图的有盖长方体纸盒,长、宽、高分别为acm,bcm,ccm,小甬的纸盒长、宽、高均为正整数,且ab=ac+3,bc=ab+ac﹣7,那么做这样一个纸盒需纸板
cm2.
三、解答题
26.如图,两个体积相同的图柱形铁块A和B,圆柱A的底面半径为2厘米,高为20厘米且比圆柱B高.(π取3)
(1)求圆柱B的底面积是多少平方厘米?
(2)如图,一个底面长8匣米,宽6厘米的长方体水箱里有一些水,将圆柱A和B立放于水箱里,水面恰好与圆柱A高度相同,求将圆柱A、B放入之前水面的高度是多少厘米?
(3)若要使水面下降至与圆柱B高度相同,需将圆柱A提起多少厘米?
27.如图①,是一个边长为10cm正方形,按要求解答下列问题:
(1)如图②,若将该正方形沿粗黑实线剪下4个边长为
cm的小正方形,拼成一个大正方形作为直四棱柱的一个底面,余下部分按虚线折叠成一个无盖直四棱柱,最后把两部分拼在一起,组成一个完整的直四棱柱,它的表面积等于原正方形的面积;
(2)若该正方形是一个圆柱的侧面展开图,求该圆柱的体积.(结果保留π)
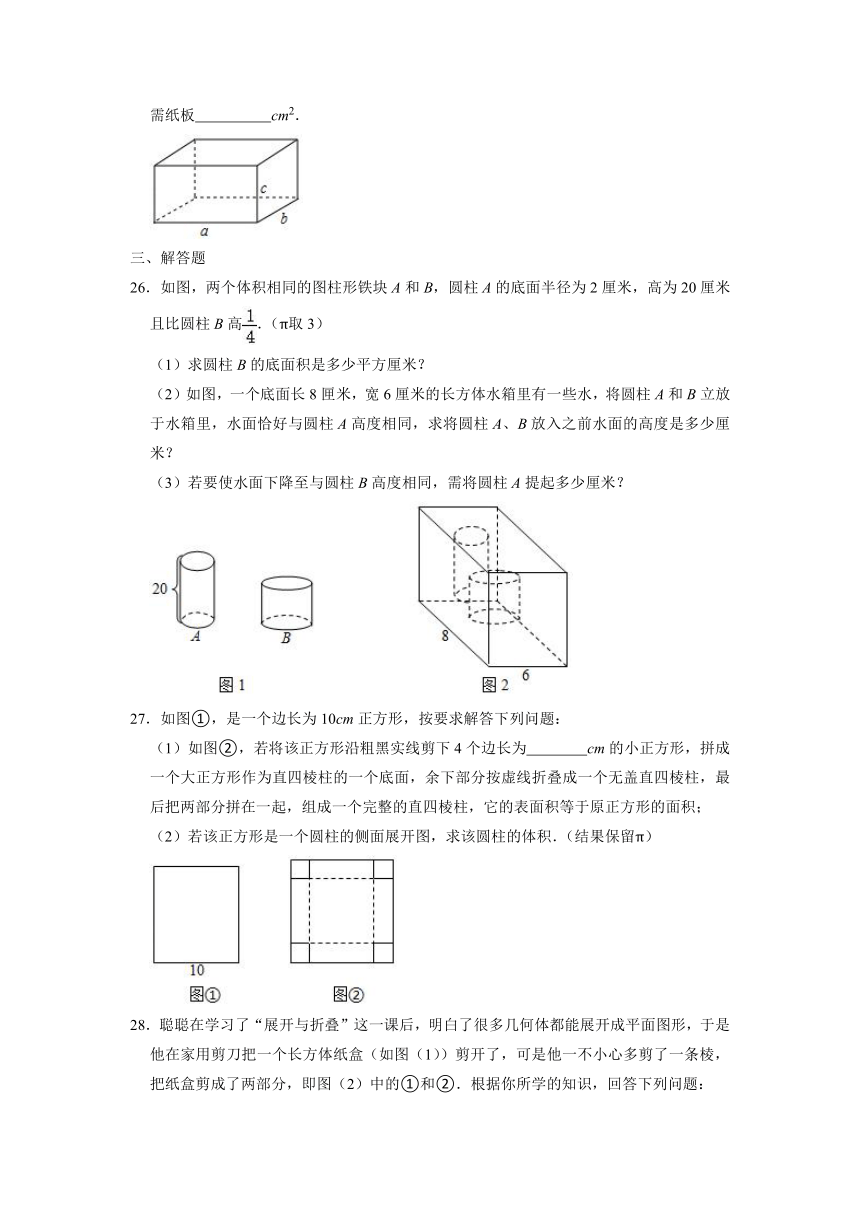
28.聪聪在学习了“展开与折叠”这一课后,明白了很多几何体都能展开成平面图形,于是他在家用剪刀把一个长方体纸盒(如图(1))剪开了,可是他一不小心多剪了一条棱,把纸盒剪成了两部分,即图(2)中的①和②.根据你所学的知识,回答下列问题:
(1)若这个长方体纸盒的长、宽、高分别是8cm,4cm,2cm,则该长方体纸盒的体积是多少?
(2)聪聪一共剪开了
条棱;
(3)现在聪聪想将剪掉的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪掉的②粘贴到①中的什么位置?请你帮助他在①上补全一种情况.
29.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到
种大小不同的几何体?
(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=πr2h,其中π取3)
30.如图所示是一张铁皮.
(1)计算该铁皮的面积;
(2)它能否做成一个长方体盒子?若能,画出长方体盒子的立体图形,并计算其体积;若不能,说明理由.
31.修建一些圆柱形的沼气池,底面直径是3m,深2m.在池的侧面与下底面抹上厚度为0.02m的水泥.(π取3.14)
(1)修建一个圆柱形的沼气池,抹水泥部分的面积是多少?
(2)如图是一个水泥罐尺寸的示意图,这个水泥罐的内部都装满水泥(水泡罐壁的厚度忽略不计).在使用水泥过程中没有损耗的情况下.这个水泥罐中的水泥最多可以满足修建多少个圆柱形的沼气池的水泥用量?
参考答案
1.解:A.正方体的主视图、左视图、俯视图都是正方形,因此选项A不符合题意;
B.三棱柱的三个侧面是长方形的,其俯视图、主视图是长方形,因此选项B不符合题意;
C.圆柱体的主视图、俯视图是长方形,因此选项C不符合题意;
D.球体的三视图都是圆形,没有矩形,因此选项D符合题意;
故选:D.
2.解:由图可知,该几何体是圆柱,
∵AD=16π,
∴底面圆的圆周长是16π,
故2πr=16π,解得r=8.
故选:C.
4.解:从左边看,底层是两个小正方形,上层左边一个小正方形,
故选:B.
5.解:原来的几何体的左视图底层是两个小正方形,若从标有①②③④的四个小正方体中取走一个或多个后,余下的几何体与原几何体的左视图相同,则取走的正方体不可能是④.
故选:A.
6.解:由俯视图易得最底层有3个正方体,由主视图第二层最少有2个正方体,
那么最少有3+2=5个立方体.
故选:A.
7.解:这是一个正方体的平面展开图,共有六个面,其中与“你”字相对的字是“成”.
故选:D.
8.解:从左面看所得到的图形,.
故选:A.
9.解:A选项有一个底面一个侧面,共两个面;
B选项有两个底面三个侧面,共五个面;
C选项有两个底面四个侧面,共六个面;
D选项有两个底面一个侧面,共三个面;
故选:C.
10.解:这是一个正方体的平面展开图,共有六个面,其中面“构”与面“谐”相对,面“建”与面“社”相对,面“和”与面“会”相对.
故选:D.
11.解:从展开图可知,该几何体有五个面,两个三角形的底面,三个长方形的侧面,因此该几何体是三棱柱,
故选:A.
12.解:三角形对应的面为DCFE,
a对应的边为DE.
故选:C.
13.解:由正方体的表面展开图的“相间、Z端是对面”可知,
“常”与“来”是对面,
“州”与“好”是对面,
“越”与“越”是对面,
翻动第1次,第2次时,“好”在前面,“州”在后面,
翻动第3次时,“好”在下面,“州”在上面,
故选:B.
14.解:直角三角形绕它的直角边旋转一周可形成圆锥.
故选:C.
15.解:∵用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,
∴最多可以截出六边形,
∴不可能截得七边形.
故选:D.
16.解:∵正方体的展开图,原正方体“4”的相对面上的数字为2,
∴原正方体“4”的相邻面上的数字分别为1,3,5,6,
∴原正方体“4”的相邻面上的数字之和是15,
故选:D.
17.解:正方体展开图的11种情况可分为“1﹣4﹣1型”6种,“2﹣3﹣1型”3种,“2﹣2﹣2型”1种,“3﹣3型”1种,
因此选项A符合题意,
故选:A.
18.解:正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.
因此不可能是七边形,
故选:D.
19.解:A、围成三棱柱时,两个三角形重合为同一底面,而另一底面没有,故不能围成直三棱柱;
B、D的两底面不是三角形,故也不能围成直三棱柱;
只有C经过折叠可以围成一个直三棱柱.
故选:C.
20.解:前后面少(3+2)×5=25(个),
上下面少的(去掉与前后面重复的)(5﹣3)+2×3+1×5=13(个),
左右面少的(去掉与前后,上下复的)(5﹣3)+(5﹣1)+(5﹣2)+(5﹣2﹣1)+(5﹣2)=14(个),
125﹣(25+13+14)=73(个),
答:图中剩下的小正方体有73个.
故答案为:73.
21.解:由正方体展开图的特征得出,折叠成正方体后,点11所在的正方形分别和点7、点1所在的两个正方形相交,
故点1与点7、点1重合.
故答案为1和7;
22.解:由图1可得,“中”和“的”相对;“国”和“我”相对;“梦”和“梦”相对;
由图2可得,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格时,“国”在下面,则这时小正方体朝上一面的字是“我”.
故答案为:我.
23.解:流星划过天空时留下一道明亮的光线,用数学知识解释为点动成线.
故答案为:点动成线.
24.解:易得2和6是相对的两个面;3和4是相对两个面;1和5是相对的2个面,
所以原正方体相对的面上的数字和的最小值是6.
故答案为:6.
25.解:∵a(b﹣c)=3,且a、b、c均为正整数,
∴或,
即,或,
①当时,代入bc=ab+ac﹣7中,得(c+3)c=c+3+c﹣7,
整理,得c2+c+4=0,此方程无实数根;
②当时,代入bc=ab+ac﹣7中,得(c+1)c=3(1+c)+3c﹣7,
整理,得c2﹣5c+4=0,
解得c=1或c=4,
∴a=3,b=2,c=1或a=3,b=5,c=4,
因此长方体的表面积为:(3×2+2×1+3×1)×2=22(cm2),或(3×5+5×4+3×4)×2=94(cm2),
故答案为:22或94.
26.解:(1)设B的底面半径为rcm,B的高为20÷(1+)=16cm,
∵A与B体积相同,
∴π×22×20=π×r2×16,
解得r2=5,
∵π=3,
∴B的底面积=πr2=15(cm2);
答:B的底面积是15平方厘米.
(2)V总=8×6×20=960(cm3),
∵VA=VB,
∴VA+VB=2VB=15×16×2=480(cm3),
∴V之前=V总﹣2VB=480(cm3),
∴之前高度==10(cm).
答:放入A、B之前的高度为10cm.
(3)当水面与B等高时V水箱=8×6×16=768(cm3),
∴相较于等A时体积相差V=960﹣768=192(cm3),
∴需将A提起高度为==16(cm).
答:需要将A圆柱提起16厘米.
27.解:(1)设粗黑实线剪下4个边长为xcm的小正方形,
根据题意列方程2x=10÷2
解得x=2.5,
故答案为:2.5;
(2)∵正方形边长为10cm,
∴圆柱的底面半径是=(cm),
∴圆柱的体积是?10=(cm3).
答:圆柱的体积是cm3.
28.解:(1)8×4×2=64(cm3)
该长方体纸盒的体积是64cm3;
(2)聪聪一共剪开了8条棱.
故答案为:8;
(3)如图,就是所画的图形(答案不唯一,有以下四种情况供参考).
29.解:(1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体.
故答案为:3.
(2)以AB为轴:
×3×82×4
=×3×64×4
=256(立方厘米);
以BC为轴:
×3×42×8
=×3×16×8
=128(立方厘米).
答:以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.
30.解:(1)(1×3+1×2+2×3)×2=22
(平方米)
答:该铁皮的面积为22平方米.
(2)能做成一个长方体的盒子,
体积为:3×1×2=6(立方米)
31.解:(1)3.14×()2+3.14×3×2=25.905(m2),
答:修建一个圆柱形的沼气池,抹水泥部分的面积是25.905m2;
(2)[3.14×()2×12+×3.14×()2×6]÷(25.905×0.02)
=98.91÷0.5181
≈190(个),
答:这个水泥罐中的水泥最多可以满足修建190个圆柱形的沼气池的水泥用量
一、选择题
1.下面四个几何体的三视图中没有矩形的是( )
A.
B.
C.
D.
2.如图,是某几何体的展开图,AD=16π,则r=( )
A.2
B.4
C.8
D.16
4.从左面观察如图所示的几何体,看到的平面图形是( )
A.
B.
C.
D.
5.如图,由七个相同的小正方体拼成立体图形,若从标有①②③④的四个小正方体中取走一个或多个后,余下的几何体与原几何体的左视图相同,则取走的正方体不可能是( )
A.④
B.③
C.②
D.①
6.由几个大小相同的小正方体搭建而成的几何体的主视图和俯视图如图所示,则搭建这个几何体所需要的小正方体的个数至少为( )
A.5
B.6
C.7
D.8
7.一个正方体的表面展开图如图所示,则与“你”字相对的面是( )
A.心
B.想
C.事
D.成
8.一个几何体由大小相同的小立方块搭成,它的俯视图如图所示,其中小正方形中的数字表示在该位置小立方块的个数,则该几何体的左视图为( )
A.
B.
C.
D.
9.下列几何体中,面的个数最多的是( )
A.
B.
C.
D.
10.如图是正方体的表面展开图,每一个面标有一个汉字,则与“和”相对的面上的字是( )
A.构
B.建
C.社
D.会
11.如图是某个几何体的展开图,该几何体是( )
A.三棱柱
B.四棱柱
C.圆柱
D.圆锥
12.将一个小正方体按图中所示方式展开.则在展开图中表示棱a的线段是( )
A.AB
B.CD
C.DE
D.CF
13.图1是一个小正方体的展开图,小正方体从图2的所示位置依次翻到第1格,第2格,第3格,这时小正方体朝上一面的字是( )
A.常
B.州
C.越
D.来
14.下列图形绕虚线旋转一周,便能形成圆锥体的是( )
A.
B.
C.
D.
15.用一平面截一个正方体,不能得到的截面形状是( )
A.等边三角形
B.长方形
C.六边形
D.七边形
16.如图所示是正方体的展开图,原正方体“4”的相邻面上的数字之和是( )
A.2
B.12
C.14
D.15
17.下列图形中不能作为正方体的展开图的是( )
A.B.C.D.
18.用一个平面去截正方体,截面图形不可能是( )
A.
B.
C.
D.
19.如图形状的四张纸板,按图中线经过折叠可以围成一个直三棱柱的是( )
A.
B.
C.
D.
二、填空题
20.一个由125个同样的小正方体组成的大正方体,从这个大正方体中抽出若干个正方体,把大正方体中相对的两面打通,结果如图,则图中剩下的小正方有
个.
21.如图是一个正方体纸盒的展开图,当折成纸盒时,与数11重合的数是
.
22.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是
.
23.流星划过天空时留下一道明亮的光线,用数学知识解释为
.
24.如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是
.
25.教师请每个同学做一个如图的有盖长方体纸盒,长、宽、高分别为acm,bcm,ccm,小甬的纸盒长、宽、高均为正整数,且ab=ac+3,bc=ab+ac﹣7,那么做这样一个纸盒需纸板
cm2.
三、解答题
26.如图,两个体积相同的图柱形铁块A和B,圆柱A的底面半径为2厘米,高为20厘米且比圆柱B高.(π取3)
(1)求圆柱B的底面积是多少平方厘米?
(2)如图,一个底面长8匣米,宽6厘米的长方体水箱里有一些水,将圆柱A和B立放于水箱里,水面恰好与圆柱A高度相同,求将圆柱A、B放入之前水面的高度是多少厘米?
(3)若要使水面下降至与圆柱B高度相同,需将圆柱A提起多少厘米?
27.如图①,是一个边长为10cm正方形,按要求解答下列问题:
(1)如图②,若将该正方形沿粗黑实线剪下4个边长为
cm的小正方形,拼成一个大正方形作为直四棱柱的一个底面,余下部分按虚线折叠成一个无盖直四棱柱,最后把两部分拼在一起,组成一个完整的直四棱柱,它的表面积等于原正方形的面积;
(2)若该正方形是一个圆柱的侧面展开图,求该圆柱的体积.(结果保留π)
28.聪聪在学习了“展开与折叠”这一课后,明白了很多几何体都能展开成平面图形,于是他在家用剪刀把一个长方体纸盒(如图(1))剪开了,可是他一不小心多剪了一条棱,把纸盒剪成了两部分,即图(2)中的①和②.根据你所学的知识,回答下列问题:
(1)若这个长方体纸盒的长、宽、高分别是8cm,4cm,2cm,则该长方体纸盒的体积是多少?
(2)聪聪一共剪开了
条棱;
(3)现在聪聪想将剪掉的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪掉的②粘贴到①中的什么位置?请你帮助他在①上补全一种情况.
29.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到
种大小不同的几何体?
(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=πr2h,其中π取3)
30.如图所示是一张铁皮.
(1)计算该铁皮的面积;
(2)它能否做成一个长方体盒子?若能,画出长方体盒子的立体图形,并计算其体积;若不能,说明理由.
31.修建一些圆柱形的沼气池,底面直径是3m,深2m.在池的侧面与下底面抹上厚度为0.02m的水泥.(π取3.14)
(1)修建一个圆柱形的沼气池,抹水泥部分的面积是多少?
(2)如图是一个水泥罐尺寸的示意图,这个水泥罐的内部都装满水泥(水泡罐壁的厚度忽略不计).在使用水泥过程中没有损耗的情况下.这个水泥罐中的水泥最多可以满足修建多少个圆柱形的沼气池的水泥用量?
参考答案
1.解:A.正方体的主视图、左视图、俯视图都是正方形,因此选项A不符合题意;
B.三棱柱的三个侧面是长方形的,其俯视图、主视图是长方形,因此选项B不符合题意;
C.圆柱体的主视图、俯视图是长方形,因此选项C不符合题意;
D.球体的三视图都是圆形,没有矩形,因此选项D符合题意;
故选:D.
2.解:由图可知,该几何体是圆柱,
∵AD=16π,
∴底面圆的圆周长是16π,
故2πr=16π,解得r=8.
故选:C.
4.解:从左边看,底层是两个小正方形,上层左边一个小正方形,
故选:B.
5.解:原来的几何体的左视图底层是两个小正方形,若从标有①②③④的四个小正方体中取走一个或多个后,余下的几何体与原几何体的左视图相同,则取走的正方体不可能是④.
故选:A.
6.解:由俯视图易得最底层有3个正方体,由主视图第二层最少有2个正方体,
那么最少有3+2=5个立方体.
故选:A.
7.解:这是一个正方体的平面展开图,共有六个面,其中与“你”字相对的字是“成”.
故选:D.
8.解:从左面看所得到的图形,.
故选:A.
9.解:A选项有一个底面一个侧面,共两个面;
B选项有两个底面三个侧面,共五个面;
C选项有两个底面四个侧面,共六个面;
D选项有两个底面一个侧面,共三个面;
故选:C.
10.解:这是一个正方体的平面展开图,共有六个面,其中面“构”与面“谐”相对,面“建”与面“社”相对,面“和”与面“会”相对.
故选:D.
11.解:从展开图可知,该几何体有五个面,两个三角形的底面,三个长方形的侧面,因此该几何体是三棱柱,
故选:A.
12.解:三角形对应的面为DCFE,
a对应的边为DE.
故选:C.
13.解:由正方体的表面展开图的“相间、Z端是对面”可知,
“常”与“来”是对面,
“州”与“好”是对面,
“越”与“越”是对面,
翻动第1次,第2次时,“好”在前面,“州”在后面,
翻动第3次时,“好”在下面,“州”在上面,
故选:B.
14.解:直角三角形绕它的直角边旋转一周可形成圆锥.
故选:C.
15.解:∵用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,
∴最多可以截出六边形,
∴不可能截得七边形.
故选:D.
16.解:∵正方体的展开图,原正方体“4”的相对面上的数字为2,
∴原正方体“4”的相邻面上的数字分别为1,3,5,6,
∴原正方体“4”的相邻面上的数字之和是15,
故选:D.
17.解:正方体展开图的11种情况可分为“1﹣4﹣1型”6种,“2﹣3﹣1型”3种,“2﹣2﹣2型”1种,“3﹣3型”1种,
因此选项A符合题意,
故选:A.
18.解:正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.
因此不可能是七边形,
故选:D.
19.解:A、围成三棱柱时,两个三角形重合为同一底面,而另一底面没有,故不能围成直三棱柱;
B、D的两底面不是三角形,故也不能围成直三棱柱;
只有C经过折叠可以围成一个直三棱柱.
故选:C.
20.解:前后面少(3+2)×5=25(个),
上下面少的(去掉与前后面重复的)(5﹣3)+2×3+1×5=13(个),
左右面少的(去掉与前后,上下复的)(5﹣3)+(5﹣1)+(5﹣2)+(5﹣2﹣1)+(5﹣2)=14(个),
125﹣(25+13+14)=73(个),
答:图中剩下的小正方体有73个.
故答案为:73.
21.解:由正方体展开图的特征得出,折叠成正方体后,点11所在的正方形分别和点7、点1所在的两个正方形相交,
故点1与点7、点1重合.
故答案为1和7;
22.解:由图1可得,“中”和“的”相对;“国”和“我”相对;“梦”和“梦”相对;
由图2可得,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格时,“国”在下面,则这时小正方体朝上一面的字是“我”.
故答案为:我.
23.解:流星划过天空时留下一道明亮的光线,用数学知识解释为点动成线.
故答案为:点动成线.
24.解:易得2和6是相对的两个面;3和4是相对两个面;1和5是相对的2个面,
所以原正方体相对的面上的数字和的最小值是6.
故答案为:6.
25.解:∵a(b﹣c)=3,且a、b、c均为正整数,
∴或,
即,或,
①当时,代入bc=ab+ac﹣7中,得(c+3)c=c+3+c﹣7,
整理,得c2+c+4=0,此方程无实数根;
②当时,代入bc=ab+ac﹣7中,得(c+1)c=3(1+c)+3c﹣7,
整理,得c2﹣5c+4=0,
解得c=1或c=4,
∴a=3,b=2,c=1或a=3,b=5,c=4,
因此长方体的表面积为:(3×2+2×1+3×1)×2=22(cm2),或(3×5+5×4+3×4)×2=94(cm2),
故答案为:22或94.
26.解:(1)设B的底面半径为rcm,B的高为20÷(1+)=16cm,
∵A与B体积相同,
∴π×22×20=π×r2×16,
解得r2=5,
∵π=3,
∴B的底面积=πr2=15(cm2);
答:B的底面积是15平方厘米.
(2)V总=8×6×20=960(cm3),
∵VA=VB,
∴VA+VB=2VB=15×16×2=480(cm3),
∴V之前=V总﹣2VB=480(cm3),
∴之前高度==10(cm).
答:放入A、B之前的高度为10cm.
(3)当水面与B等高时V水箱=8×6×16=768(cm3),
∴相较于等A时体积相差V=960﹣768=192(cm3),
∴需将A提起高度为==16(cm).
答:需要将A圆柱提起16厘米.
27.解:(1)设粗黑实线剪下4个边长为xcm的小正方形,
根据题意列方程2x=10÷2
解得x=2.5,
故答案为:2.5;
(2)∵正方形边长为10cm,
∴圆柱的底面半径是=(cm),
∴圆柱的体积是?10=(cm3).
答:圆柱的体积是cm3.
28.解:(1)8×4×2=64(cm3)
该长方体纸盒的体积是64cm3;
(2)聪聪一共剪开了8条棱.
故答案为:8;
(3)如图,就是所画的图形(答案不唯一,有以下四种情况供参考).
29.解:(1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体.
故答案为:3.
(2)以AB为轴:
×3×82×4
=×3×64×4
=256(立方厘米);
以BC为轴:
×3×42×8
=×3×16×8
=128(立方厘米).
答:以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.
30.解:(1)(1×3+1×2+2×3)×2=22
(平方米)
答:该铁皮的面积为22平方米.
(2)能做成一个长方体的盒子,
体积为:3×1×2=6(立方米)
31.解:(1)3.14×()2+3.14×3×2=25.905(m2),
答:修建一个圆柱形的沼气池,抹水泥部分的面积是25.905m2;
(2)[3.14×()2×12+×3.14×()2×6]÷(25.905×0.02)
=98.91÷0.5181
≈190(个),
答:这个水泥罐中的水泥最多可以满足修建190个圆柱形的沼气池的水泥用量
