《第2章轴对称》同步能力达标测评(附答案) 2021-2022学年鲁教版(五四制)七年级数学上册(word版含解析)
文档属性
| 名称 | 《第2章轴对称》同步能力达标测评(附答案) 2021-2022学年鲁教版(五四制)七年级数学上册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 360.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 22:11:21 | ||
图片预览




文档简介
2021-2022学年鲁教版七年级数学上册《第2章轴对称》同步能力达标测评(附答案)
一.选择题(共10小题,每小题3分,共计30分)
1.等腰三角形的一边长9cm,另一边长4cm,则它的周长是( )
A.22
cm
B.17
cm
C.22cm或17cm
D.无法确定
2.如图,在△ABC中,AD是∠BAC的平分线,DE⊥AC,垂足为E,若AB=12,DE=4,则△ABD的面积是( )
A.4
B.12
C.24
D.48
3.在△ABC中,AB=AC,∠BAC=108°,AC的中垂线交BC于点D,交AC于点E,连接AD,∠ADB的角平分线交AB于点F则图中等腰三角形的个数为( )
A.6
B.5
C.4
D.3
4.如图,△ABC中,AB=AC,∠BAC=100°,AD是BC边上的中线,CE平分∠BCA交AB于点E,AD、CE相交于点F,则∠CFA的度数是( )
A.100°
B.105°
C.110°
D.120°
5.如图,等边△ABC,边长为8,点D为边BC上一点,以AD为边在AD右侧作等边△ADE,连接CE,当△ADE周长最小时,CE的长度为( )
A.1
B.2
C.4
D.8
6.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列结论:
①EF=BE+CF;②点O到△ABC各边的距离相等;
③∠BOC=90°+∠A;④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的个数为( )
A.1
B.2
C.3
D.4
7.如图,在△ABC中,∠ABC和∠ACB的外角平分线BP、CP交于点P,PE⊥AC于点E,若S△BPC=6,PE=4,S△ABC=8,则△ABC的周长为( )
A.9
B.10
C.11
D.12
8.如图,在△ABC中,BD⊥AC于点D,CE平分∠ACB,与BD交于点E,若BC=5,△BCE的面积为5,则ED的长为( )
A.
B.1
C.2
D.5
9.如图,三条公路两两相交,现计划修建一个油库,计划使得该油库到三条公路的距离相等,则油库的可选位置有( )处.
A.1
B.2
C.3
D.4
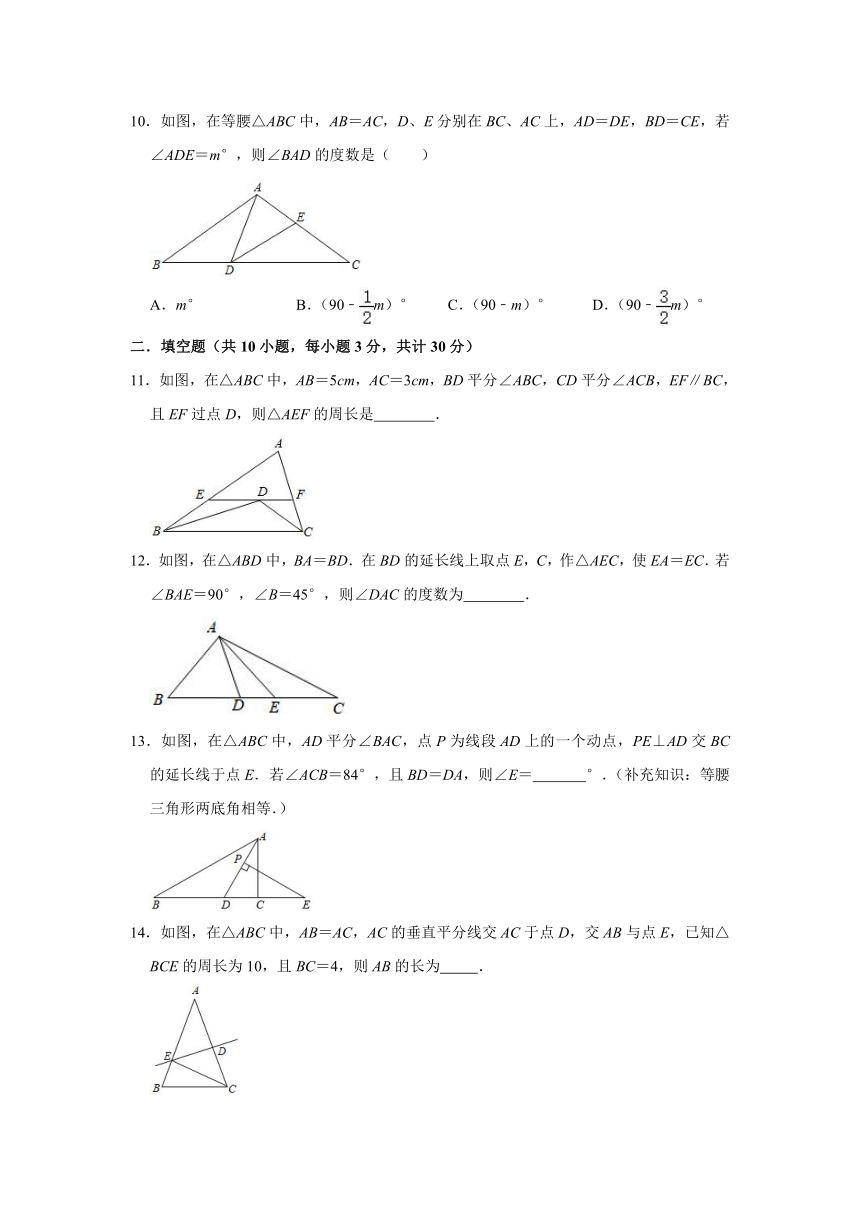
10.如图,在等腰△ABC中,AB=AC,D、E分别在BC、AC上,AD=DE,BD=CE,若∠ADE=m°,则∠BAD的度数是( )
A.m°
B.(90﹣m)°
C.(90﹣m)°
D.(90﹣m)°
二.填空题(共10小题,每小题3分,共计30分)
11.如图,在△ABC中,AB=5cm,AC=3cm,BD平分∠ABC,CD平分∠ACB,EF∥BC,且EF过点D,则△AEF的周长是
.
12.如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,则∠DAC的度数为
.
13.如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.若∠ACB=84°,且BD=DA,则∠E=
°.(补充知识:等腰三角形两底角相等.)
14.如图,在△ABC中,AB=AC,AC的垂直平分线交AC于点D,交AB与点E,已知△BCE的周长为10,且BC=4,则AB的长为
.
15.已知△ABC中,AB=AC,AD是BC边上的中线,且∠BAD=40°.点E是边AC上的一点,若△ADE为等腰三角形,则∠EDC的度数是
.
16.如图,△ABC的面积为6cm2,AP垂直∠ABC的平分线BP于点P,则△PBC的面积是
cm2.
17.已知在等腰△ABC中,AD⊥BC于点D,且BC=2AD,则等腰△ABC底角的度数为
.
18.如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是
.
19.如图,在△ABC中,AB=AC=5,AD是∠BAC的平分线,BC=6,AD=4,若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是
.
20.已知:△ABC是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、Q同时在不等边△ABC的内部时,∠BOC=100度,那么∠BPC=
.
三.解答题(共6小题,每小题10分,共计60分)
21.如图,在△ABC中,DM,EN分别垂直平分边AC和边BC,交边AB于M,N两点,DM与EN相交于点F.
(1)若AB=3cm,求△CMN的周长.
(2)若∠MFN=70°,求∠MCN的度数.
22.已知,在△ABC中,∠ABC=∠ACB,点D为射线CB上一点,过点D作DE⊥AC于点E.
(1)如图1,当点D在线段BC上时,请直接写出∠BAC与∠EDC的数量关系:
.
(2)如图2,当点D在CB的延长线上时,画出图形,探究∠BAC与∠EDC的数量关系,并说明理由.
(3)在(2)的条件下,点F为线段BC上一点,过点F作FG⊥AC于点G,连接AF,且∠AFG=∠CFG,∠BAF=∠BFA,延长ED、AB交于点K,求∠EKA的度数.
23.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC=
°,∠DEC=
°;点D从B向C运动时,∠BDA逐渐变
(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
24.如图,在△ABC中,∠ABC=90°,BD是AC边上的高,AE是∠BAC的角平分线,分别交BD、BC于点G、E,过点B作AE的垂线BF,分别交AE、AC于点H、F.
(1)求证:BF平分∠DBC;
(2)若∠ABF=3∠C,求∠C的度数.
25.如图△ABC中,AB=AC,∠ABC的平分线BE交AC于点D,AF⊥AB交BE于点F.
(1)如图1,若∠BAC=40°,求∠AFE的度数.
(2)如图2,若BD⊥AC,垂足为D,BF=8,求DF的长.
26.17.已知,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
(1)【特殊情况,探索结论】如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:AE
DB(填“>”、“<”或“=”).
(2)【特例启发,解答题目】如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE
DB(填“>”、“<”或“=”);理由如下,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程).
(3)【拓展结论,设计新题】
在等边三角形ABC中,点E在直线AB上,点D在线段CB的延长线上,且ED=EC,若△ABC的边长为1,AE=2,求CD的长(请你画出相应图形,并直接写出结果).
参考答案
一.选择题(共10小题,每小题3分,共计30分)
1.解:①当腰为4cm时,三边为4cm,4cm,9cm,
∵4+4<9,
∴不符合三角形的三边关系定理,此种情况舍去;
②当腰为9cm时,三边为4cm,9cm,9cm,
此时符合三角形的三边关系定理,
此时等腰三角形的周长是4cm+9cm+9cm=22cm,
故选:A.
2.解:过D点作DF⊥AB于F,如图,
∵AD是∠BAC的平分线,DE⊥AC,DF⊥AB,
∴DF=DE=4,
∴S△ABD=×12×4=24.
故选:C.
3.解:∵AB=AC,∠BAC=108°,
∴∠B=∠C=36°,△ABC是等腰三角形,
∵DE是AC的中垂线,
∴AD=CD,△ADC是等腰三角形,
∴∠DAC=∠C=36°,∠BAD=108°﹣36°=72°,
∵∠B=36°,
∴∠BDA=180°﹣36°﹣72°=72°,
∴∠BAD=∠BDA,△ABD是等腰三角形,
∵DF平分∠ADB,∠ADB=72°,
∴∠BDF=∠ADF=36°,
∴△ADF和△BDF是等腰三角形.
故选:B.
4.解:在△ABC中,AB=AC,∠BAC=100°,
∴∠ACB=(180°﹣100°)÷2=40°,
∵CE平分∠BCA,
∴∠BCE=20°,
∵AD是BC边上的中线,
∴∠ADC=90°,
∴∠CFA=90°+20°=110°.
故选:C.
5.解:
∵△ADE是等边三角形,
∴AD=DE=AE,
∴C△ADE=3AD,
当△ADE周长最小时,
即AD最小,
当AD⊥BC时,AD最小,
此时,BD=AB?sin30°=4,
∵△ABC是等边三角形,
∴∠1+∠2=60°,
又∵∠2+∠3=60°,
∴∠1=∠3,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE=4,
故选:C.
6.解:在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°﹣∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+∠A;故③正确;
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=AE?OM+AF?OD=OD?(AE+AF)=mn;故④错误;
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故②正确.
故选:C.
7.解:如图,过点P作PF⊥BC于F,作PG⊥AB于G,连接AP,
∵∠ABC和∠ACB的外角平分线BP、CP交于P,
∴PF=PG=PE=4,
∵S△BPC=6,
∴×BC×4=6,
解得,BC=3,
∵S△ABC=S△ACP+S△ABP﹣S△BCP,
=×(AB+AC)×4﹣6
=8,
∴AB+AC=7,
∴△ABC的周长=AB+AC+BC=10,
故选:B.
8.解:过点E作EF⊥BC于F,
∵△BCE的面积为5,
∴×BC×EF=5,即×5×EF=5,
解得,EF=2,
∵CE平分∠ACB,ED⊥AC,EF⊥BC,
∴ED=EF=2,
故选:C.
9.解:如图,油库的可选位置有4处.
故选:D.
10.解:分别过点E、D作EF⊥CD、DG⊥AB,垂直分别为F、G,
∵AB=AC,
∴∠B=∠C,
∵EF⊥CD,DG⊥AB,
∴∠EFC=∠DGB=90°,
在△CEF和△BDG中
∴△CEF≌△DGB(AAS),
∴EF=DG,
在Rt△DEF和Rt△ADG中
∴Rt△DEF≌Rt△ADG(HL),
∴∠CED=∠ADB,∠EDC=∠DAB,
∵AD=ED,∠ADE=m°,
∴∠DEA=()°,
∴∠ADB=∠CED=(180﹣)°,
∴∠BAD=∠EDC=180°﹣(∠ADB+∠ADE)=180°﹣(180﹣+m)°=(90﹣m)°.
故选:D.
二.填空题(共10小题,每小题3分,共计30分)
11.解:∵EF∥BC,
∴∠DBC=∠BDE,∠DCB=∠CDF
∵BD、CD分别是∠ABC和∠ACB的角平分线,
∴∠DBC=∠DBE=∠BDE,∠FCD=∠DCB=∠CDF,
∴DE=BE,DF=CF,
∴△AEF的周长=AF+FE+AE=AF+DF+DE+AE=AF+CF+BE+AE=AB+AC,
∵AB=5cm,AC=3cm,
∴△AEF的周长=8cm,
故答案为:8cm.
12.解:∵EA=EC,
∴∠EAC=∠C,
∵BA=BD,
∴∠BAD=∠BDA,
∴∠ADB=∠BAD=(180°﹣45°)=67.5°,
∵∠BAE=90°,∠B=45°,
∵∠AEB=∠B=45°,∠EAC=∠C,
∴∠EAC=22.5°,
∴∠DAE=∠DAE+∠EAC=45°,
故答案为:45°.
13.解:∵BD=AD,
∴∠B=∠BAD,
∵AD平分∠BAC,
∴∠BAC=2∠BAD=2∠B,
∵∠B+∠BAC+∠ACB=180°,∠ACB=84°,
∴∠B+2∠B+84°=180°,
解得∠B=32°,
∵∠ADC=∠B+∠BAD=2∠B,
∴∠ADC=64°,
∵PE⊥AD交BC的延长线于点E.
∴∠E+∠ADC=90°,
解得∠E=26°.
故答案为26.
14.解:∵DE是AB的垂直平分线,
∴AE=CE,
∵△BCE的周长为10,BC=4,
∴4+BE+CE=10,
∵AE=CE,
∴AE+BE=10﹣4=6,
∴AB=AE+BE=6.
故答案为:6.
15.解:∵AB=AC,AD是BC边上的中线,且∠BAD=40°,
∴∠CAD=∠BAD=40°,∠ADC=90°,
①AE1=DE1时,
∠ADE1=∠CAD=40°,
则∠E1DC=90°﹣40°=50°;
②AE2=AD时,
∠ADE2=∠AE2D=(180°﹣40°)÷2=70°,
则∠E2DC=90°﹣70°=20°.
故∠EDC的度数是50°或20°.
故答案为:50°或20°.
16.解:延长AP交BC于点E,如图所示.
∵AP垂直∠ABC的平分线BP于点P,
∴∠ABP=∠EBP.
在△ABP和△EBP中,
,
∴△ABP≌△EBP(ASA),
∴AP=EP.
∵△APC和△EPC等底同高,
∴S△APC=S△CPE,
∴S△PBC=S△BPE+S△CPE=S△ABC=×6=3(cm2),
故答案为:3.
17.解:①当AB=AC时,∵△ABC是等腰三角形,
∴AB=AC.
∵AD⊥BC,
∴BD=DC,∠ADB=90°.
∵BC=2AD,
∴BD=AD.
∴∠B=∠BAD.
∵∠B+∠BAD=90°,
∴∠B=45°.
②当CA=CB时,在Rt△ADC中,AC=2AD,
∴∠C=30°,
∴∠B=∠CAB=75°,
③当AB=BC时,在Rt△ADB中,
∵AD=BC,AB=BC,
∴AD=AB,
∴∠DBA=30°,
∴∠BAC=∠BCA=15°.
故答案为:15°或45°或75°.
18.解:如连接BE,与AD交于点P,此时PE+PC最小,
∵△ABC是等边三角形,AD⊥BC,
∴PC=PB,
∴PE+PC=PB+PE=BE,
即BE就是PE+PC的最小值,
∵△ABC是等边三角形,
∴∠BCE=60°,
∵BA=BC,AE=EC,
∴BE⊥AC,
∴∠BEC=90°,
∴∠EBC=30°,
∵PB=PC,
∴∠PCB=∠PBC=30°,
∴∠CPE=∠PBC+∠PCB=60°,
故答案为60°.
19.解:∵AB=AC,AD是∠BAC的平分线,
∴AD垂直平分BC,
∴BP=CP.
如图,过点B作BQ⊥AC于点Q,BQ交AD于点P,则此时PC+PQ取最小值,最小值为BQ的长,如图所示.
∵S△ABC=BC?AD=AC?BQ,
∴BQ==,
即PC+PQ的最小值是.
故答案为:.
20.解:连接AO,
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=90°+∠BAC,
∵点O是这个三角形三边垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,∠OBC=∠OCB,
∴∠AOB=180°﹣2∠OAB,∠AOC=180°﹣2∠OAC,
∴∠BOC=360°﹣(∠AOB+∠AOC),
=360°﹣(180°﹣2∠OAB+180°﹣2∠OAC),
=2∠OAB+2∠OAC
=2∠BAC,
∴2∠BAC=100°,
解得,∠BAC=50°,
∴∠BPC=90°+×50°=115°,
故答案为:115°.
三.解答题(共6小题,每小题10分,共计60分)
21.解:(1)∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB=3(cm);
(2)∵∠MFN=70°,
∴∠MNF+∠NMF=180°﹣70°=110°,
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠MNF+∠NMF=110°,
∴∠A+∠B=90°﹣∠AMD+90°﹣∠BNE=180°﹣110°=70°,
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°﹣2(∠A+∠B)=180°﹣2×70°=40°.
22.(1)如图1中,作AH⊥BC于H.
∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH,
∵DE⊥AC,
∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.
故答案为∠BAC=2∠EDC.
(2)如图2中,结论:∠BAC=2∠EDC.
理由:∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH,
∵DE⊥AC,
∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.
(3)如图2中,设∠C=∠FAC=∠ABC=x,则∠BAF=∠BFA=2x,
∴5x=180°,
∴x=36°,
∴∠EAK=∠ABC+∠C=72°,
∵KE⊥EC,
∴∠E=90°,
∴∠EKA=90°﹣72°=18°.
23.解:(1)∠EDC=180°﹣∠ADB﹣∠ADE=180°﹣115°﹣40°=25°,
∠DEC=180°﹣∠EDC﹣∠C=180°﹣40°﹣25°=115°,
∠BDA逐渐变小;
故答案为:25°,115°,小;
(2)当DC=2时,△ABD≌△DCE,
理由:∵∠C=40°,
∴∠DEC+∠EDC=140°,
又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC,
又∵AB=DC=2,
∴△ABD≌△DCE(AAS),
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,
理由:∵∠BDA=110°时,
∴∠ADC=70°,
∵∠C=40°,
∴∠DAC=70°,∠AED=∠C+∠EDC=30°+40°=70°,
∴∠DAC=∠AED,
∴△ADE的形状是等腰三角形;
∵当∠BDA的度数为80°时,
∴∠ADC=100°,
∵∠C=40°,
∴∠DAC=40°,
∴∠DAC=∠ADE,
∴△ADE的形状是等腰三角形.
24.(1)证明:∵BD⊥AC,
∴∠BDC=90°,
∵∠ABC=90°,
∴∠ABD+∠DBC=90°,∠DBC+∠C=90°,
∴∠ABD=∠C,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠BGE=∠ABD+∠BAE,∠BEG=∠C+∠EAC,
∴∠BGE=∠BEG,
∴BG=BE,
∵BF⊥EG,
∴BF平分∠DBC.
(2)解:∵∠ABF=3∠C,∠ABD=∠C,BF平分∠DBC,
∴∠FBD=∠FBC=2∠C,
∴5∠C=90°,
∴∠C=18°.
25.解:(1)∵AB=AC,∠BAC=40°,
∴∠ABC=70°,
∵BE平分∠ABC,
∴∠ABF=35°,
∵AF⊥AB,
∴∠BAF=90°,
∴∠AFE=125°.
(2)∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵BD⊥AC,
∴∠ADB=CDB=90°,
∴△ABD≌△CBD(ASA),
∴AB=BC,
∵AB=AC,
∴三角形ABC是等边三角形,
∴∠ABF=30°,
∴AF=4,
在Rt△ADF中,
DF=2.
26.解:(1)当E为AB的中点时,AE=DB;
(2)AE=DB,理由如下,过点E作EF∥BC,交AC于点F,
证明:∵△ABC为等边三角形,
∴△AEF为等边三角形,
∴AE=EF,BE=CF,
∵ED=EC,
∴∠D=∠ECD,
∵∠DEB=60°﹣∠D,∠ECF=60°﹣∠ECD,
∴∠DEB=∠ECF,
在△DBE和△EFC中,
,
∴△DBE≌△EFC(SAS),
∴DB=EF,
则AE=DB;
(3)点E在AB延长线上时,如图所示,同理可得△DBE≌△EFC,
∴DB=EF=2,BC=1,
则CD=BC+DB=3.
故答案为:(1)=;(2)=
一.选择题(共10小题,每小题3分,共计30分)
1.等腰三角形的一边长9cm,另一边长4cm,则它的周长是( )
A.22
cm
B.17
cm
C.22cm或17cm
D.无法确定
2.如图,在△ABC中,AD是∠BAC的平分线,DE⊥AC,垂足为E,若AB=12,DE=4,则△ABD的面积是( )
A.4
B.12
C.24
D.48
3.在△ABC中,AB=AC,∠BAC=108°,AC的中垂线交BC于点D,交AC于点E,连接AD,∠ADB的角平分线交AB于点F则图中等腰三角形的个数为( )
A.6
B.5
C.4
D.3
4.如图,△ABC中,AB=AC,∠BAC=100°,AD是BC边上的中线,CE平分∠BCA交AB于点E,AD、CE相交于点F,则∠CFA的度数是( )
A.100°
B.105°
C.110°
D.120°
5.如图,等边△ABC,边长为8,点D为边BC上一点,以AD为边在AD右侧作等边△ADE,连接CE,当△ADE周长最小时,CE的长度为( )
A.1
B.2
C.4
D.8
6.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列结论:
①EF=BE+CF;②点O到△ABC各边的距离相等;
③∠BOC=90°+∠A;④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的个数为( )
A.1
B.2
C.3
D.4
7.如图,在△ABC中,∠ABC和∠ACB的外角平分线BP、CP交于点P,PE⊥AC于点E,若S△BPC=6,PE=4,S△ABC=8,则△ABC的周长为( )
A.9
B.10
C.11
D.12
8.如图,在△ABC中,BD⊥AC于点D,CE平分∠ACB,与BD交于点E,若BC=5,△BCE的面积为5,则ED的长为( )
A.
B.1
C.2
D.5
9.如图,三条公路两两相交,现计划修建一个油库,计划使得该油库到三条公路的距离相等,则油库的可选位置有( )处.
A.1
B.2
C.3
D.4
10.如图,在等腰△ABC中,AB=AC,D、E分别在BC、AC上,AD=DE,BD=CE,若∠ADE=m°,则∠BAD的度数是( )
A.m°
B.(90﹣m)°
C.(90﹣m)°
D.(90﹣m)°
二.填空题(共10小题,每小题3分,共计30分)
11.如图,在△ABC中,AB=5cm,AC=3cm,BD平分∠ABC,CD平分∠ACB,EF∥BC,且EF过点D,则△AEF的周长是
.
12.如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,则∠DAC的度数为
.
13.如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.若∠ACB=84°,且BD=DA,则∠E=
°.(补充知识:等腰三角形两底角相等.)
14.如图,在△ABC中,AB=AC,AC的垂直平分线交AC于点D,交AB与点E,已知△BCE的周长为10,且BC=4,则AB的长为
.
15.已知△ABC中,AB=AC,AD是BC边上的中线,且∠BAD=40°.点E是边AC上的一点,若△ADE为等腰三角形,则∠EDC的度数是
.
16.如图,△ABC的面积为6cm2,AP垂直∠ABC的平分线BP于点P,则△PBC的面积是
cm2.
17.已知在等腰△ABC中,AD⊥BC于点D,且BC=2AD,则等腰△ABC底角的度数为
.
18.如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是
.
19.如图,在△ABC中,AB=AC=5,AD是∠BAC的平分线,BC=6,AD=4,若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是
.
20.已知:△ABC是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、Q同时在不等边△ABC的内部时,∠BOC=100度,那么∠BPC=
.
三.解答题(共6小题,每小题10分,共计60分)
21.如图,在△ABC中,DM,EN分别垂直平分边AC和边BC,交边AB于M,N两点,DM与EN相交于点F.
(1)若AB=3cm,求△CMN的周长.
(2)若∠MFN=70°,求∠MCN的度数.
22.已知,在△ABC中,∠ABC=∠ACB,点D为射线CB上一点,过点D作DE⊥AC于点E.
(1)如图1,当点D在线段BC上时,请直接写出∠BAC与∠EDC的数量关系:
.
(2)如图2,当点D在CB的延长线上时,画出图形,探究∠BAC与∠EDC的数量关系,并说明理由.
(3)在(2)的条件下,点F为线段BC上一点,过点F作FG⊥AC于点G,连接AF,且∠AFG=∠CFG,∠BAF=∠BFA,延长ED、AB交于点K,求∠EKA的度数.
23.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC=
°,∠DEC=
°;点D从B向C运动时,∠BDA逐渐变
(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
24.如图,在△ABC中,∠ABC=90°,BD是AC边上的高,AE是∠BAC的角平分线,分别交BD、BC于点G、E,过点B作AE的垂线BF,分别交AE、AC于点H、F.
(1)求证:BF平分∠DBC;
(2)若∠ABF=3∠C,求∠C的度数.
25.如图△ABC中,AB=AC,∠ABC的平分线BE交AC于点D,AF⊥AB交BE于点F.
(1)如图1,若∠BAC=40°,求∠AFE的度数.
(2)如图2,若BD⊥AC,垂足为D,BF=8,求DF的长.
26.17.已知,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
(1)【特殊情况,探索结论】如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:AE
DB(填“>”、“<”或“=”).
(2)【特例启发,解答题目】如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE
DB(填“>”、“<”或“=”);理由如下,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程).
(3)【拓展结论,设计新题】
在等边三角形ABC中,点E在直线AB上,点D在线段CB的延长线上,且ED=EC,若△ABC的边长为1,AE=2,求CD的长(请你画出相应图形,并直接写出结果).
参考答案
一.选择题(共10小题,每小题3分,共计30分)
1.解:①当腰为4cm时,三边为4cm,4cm,9cm,
∵4+4<9,
∴不符合三角形的三边关系定理,此种情况舍去;
②当腰为9cm时,三边为4cm,9cm,9cm,
此时符合三角形的三边关系定理,
此时等腰三角形的周长是4cm+9cm+9cm=22cm,
故选:A.
2.解:过D点作DF⊥AB于F,如图,
∵AD是∠BAC的平分线,DE⊥AC,DF⊥AB,
∴DF=DE=4,
∴S△ABD=×12×4=24.
故选:C.
3.解:∵AB=AC,∠BAC=108°,
∴∠B=∠C=36°,△ABC是等腰三角形,
∵DE是AC的中垂线,
∴AD=CD,△ADC是等腰三角形,
∴∠DAC=∠C=36°,∠BAD=108°﹣36°=72°,
∵∠B=36°,
∴∠BDA=180°﹣36°﹣72°=72°,
∴∠BAD=∠BDA,△ABD是等腰三角形,
∵DF平分∠ADB,∠ADB=72°,
∴∠BDF=∠ADF=36°,
∴△ADF和△BDF是等腰三角形.
故选:B.
4.解:在△ABC中,AB=AC,∠BAC=100°,
∴∠ACB=(180°﹣100°)÷2=40°,
∵CE平分∠BCA,
∴∠BCE=20°,
∵AD是BC边上的中线,
∴∠ADC=90°,
∴∠CFA=90°+20°=110°.
故选:C.
5.解:
∵△ADE是等边三角形,
∴AD=DE=AE,
∴C△ADE=3AD,
当△ADE周长最小时,
即AD最小,
当AD⊥BC时,AD最小,
此时,BD=AB?sin30°=4,
∵△ABC是等边三角形,
∴∠1+∠2=60°,
又∵∠2+∠3=60°,
∴∠1=∠3,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE=4,
故选:C.
6.解:在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°﹣∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+∠A;故③正确;
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=AE?OM+AF?OD=OD?(AE+AF)=mn;故④错误;
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故②正确.
故选:C.
7.解:如图,过点P作PF⊥BC于F,作PG⊥AB于G,连接AP,
∵∠ABC和∠ACB的外角平分线BP、CP交于P,
∴PF=PG=PE=4,
∵S△BPC=6,
∴×BC×4=6,
解得,BC=3,
∵S△ABC=S△ACP+S△ABP﹣S△BCP,
=×(AB+AC)×4﹣6
=8,
∴AB+AC=7,
∴△ABC的周长=AB+AC+BC=10,
故选:B.
8.解:过点E作EF⊥BC于F,
∵△BCE的面积为5,
∴×BC×EF=5,即×5×EF=5,
解得,EF=2,
∵CE平分∠ACB,ED⊥AC,EF⊥BC,
∴ED=EF=2,
故选:C.
9.解:如图,油库的可选位置有4处.
故选:D.
10.解:分别过点E、D作EF⊥CD、DG⊥AB,垂直分别为F、G,
∵AB=AC,
∴∠B=∠C,
∵EF⊥CD,DG⊥AB,
∴∠EFC=∠DGB=90°,
在△CEF和△BDG中
∴△CEF≌△DGB(AAS),
∴EF=DG,
在Rt△DEF和Rt△ADG中
∴Rt△DEF≌Rt△ADG(HL),
∴∠CED=∠ADB,∠EDC=∠DAB,
∵AD=ED,∠ADE=m°,
∴∠DEA=()°,
∴∠ADB=∠CED=(180﹣)°,
∴∠BAD=∠EDC=180°﹣(∠ADB+∠ADE)=180°﹣(180﹣+m)°=(90﹣m)°.
故选:D.
二.填空题(共10小题,每小题3分,共计30分)
11.解:∵EF∥BC,
∴∠DBC=∠BDE,∠DCB=∠CDF
∵BD、CD分别是∠ABC和∠ACB的角平分线,
∴∠DBC=∠DBE=∠BDE,∠FCD=∠DCB=∠CDF,
∴DE=BE,DF=CF,
∴△AEF的周长=AF+FE+AE=AF+DF+DE+AE=AF+CF+BE+AE=AB+AC,
∵AB=5cm,AC=3cm,
∴△AEF的周长=8cm,
故答案为:8cm.
12.解:∵EA=EC,
∴∠EAC=∠C,
∵BA=BD,
∴∠BAD=∠BDA,
∴∠ADB=∠BAD=(180°﹣45°)=67.5°,
∵∠BAE=90°,∠B=45°,
∵∠AEB=∠B=45°,∠EAC=∠C,
∴∠EAC=22.5°,
∴∠DAE=∠DAE+∠EAC=45°,
故答案为:45°.
13.解:∵BD=AD,
∴∠B=∠BAD,
∵AD平分∠BAC,
∴∠BAC=2∠BAD=2∠B,
∵∠B+∠BAC+∠ACB=180°,∠ACB=84°,
∴∠B+2∠B+84°=180°,
解得∠B=32°,
∵∠ADC=∠B+∠BAD=2∠B,
∴∠ADC=64°,
∵PE⊥AD交BC的延长线于点E.
∴∠E+∠ADC=90°,
解得∠E=26°.
故答案为26.
14.解:∵DE是AB的垂直平分线,
∴AE=CE,
∵△BCE的周长为10,BC=4,
∴4+BE+CE=10,
∵AE=CE,
∴AE+BE=10﹣4=6,
∴AB=AE+BE=6.
故答案为:6.
15.解:∵AB=AC,AD是BC边上的中线,且∠BAD=40°,
∴∠CAD=∠BAD=40°,∠ADC=90°,
①AE1=DE1时,
∠ADE1=∠CAD=40°,
则∠E1DC=90°﹣40°=50°;
②AE2=AD时,
∠ADE2=∠AE2D=(180°﹣40°)÷2=70°,
则∠E2DC=90°﹣70°=20°.
故∠EDC的度数是50°或20°.
故答案为:50°或20°.
16.解:延长AP交BC于点E,如图所示.
∵AP垂直∠ABC的平分线BP于点P,
∴∠ABP=∠EBP.
在△ABP和△EBP中,
,
∴△ABP≌△EBP(ASA),
∴AP=EP.
∵△APC和△EPC等底同高,
∴S△APC=S△CPE,
∴S△PBC=S△BPE+S△CPE=S△ABC=×6=3(cm2),
故答案为:3.
17.解:①当AB=AC时,∵△ABC是等腰三角形,
∴AB=AC.
∵AD⊥BC,
∴BD=DC,∠ADB=90°.
∵BC=2AD,
∴BD=AD.
∴∠B=∠BAD.
∵∠B+∠BAD=90°,
∴∠B=45°.
②当CA=CB时,在Rt△ADC中,AC=2AD,
∴∠C=30°,
∴∠B=∠CAB=75°,
③当AB=BC时,在Rt△ADB中,
∵AD=BC,AB=BC,
∴AD=AB,
∴∠DBA=30°,
∴∠BAC=∠BCA=15°.
故答案为:15°或45°或75°.
18.解:如连接BE,与AD交于点P,此时PE+PC最小,
∵△ABC是等边三角形,AD⊥BC,
∴PC=PB,
∴PE+PC=PB+PE=BE,
即BE就是PE+PC的最小值,
∵△ABC是等边三角形,
∴∠BCE=60°,
∵BA=BC,AE=EC,
∴BE⊥AC,
∴∠BEC=90°,
∴∠EBC=30°,
∵PB=PC,
∴∠PCB=∠PBC=30°,
∴∠CPE=∠PBC+∠PCB=60°,
故答案为60°.
19.解:∵AB=AC,AD是∠BAC的平分线,
∴AD垂直平分BC,
∴BP=CP.
如图,过点B作BQ⊥AC于点Q,BQ交AD于点P,则此时PC+PQ取最小值,最小值为BQ的长,如图所示.
∵S△ABC=BC?AD=AC?BQ,
∴BQ==,
即PC+PQ的最小值是.
故答案为:.
20.解:连接AO,
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=90°+∠BAC,
∵点O是这个三角形三边垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,∠OBC=∠OCB,
∴∠AOB=180°﹣2∠OAB,∠AOC=180°﹣2∠OAC,
∴∠BOC=360°﹣(∠AOB+∠AOC),
=360°﹣(180°﹣2∠OAB+180°﹣2∠OAC),
=2∠OAB+2∠OAC
=2∠BAC,
∴2∠BAC=100°,
解得,∠BAC=50°,
∴∠BPC=90°+×50°=115°,
故答案为:115°.
三.解答题(共6小题,每小题10分,共计60分)
21.解:(1)∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB=3(cm);
(2)∵∠MFN=70°,
∴∠MNF+∠NMF=180°﹣70°=110°,
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠MNF+∠NMF=110°,
∴∠A+∠B=90°﹣∠AMD+90°﹣∠BNE=180°﹣110°=70°,
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°﹣2(∠A+∠B)=180°﹣2×70°=40°.
22.(1)如图1中,作AH⊥BC于H.
∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH,
∵DE⊥AC,
∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.
故答案为∠BAC=2∠EDC.
(2)如图2中,结论:∠BAC=2∠EDC.
理由:∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH,
∵DE⊥AC,
∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.
(3)如图2中,设∠C=∠FAC=∠ABC=x,则∠BAF=∠BFA=2x,
∴5x=180°,
∴x=36°,
∴∠EAK=∠ABC+∠C=72°,
∵KE⊥EC,
∴∠E=90°,
∴∠EKA=90°﹣72°=18°.
23.解:(1)∠EDC=180°﹣∠ADB﹣∠ADE=180°﹣115°﹣40°=25°,
∠DEC=180°﹣∠EDC﹣∠C=180°﹣40°﹣25°=115°,
∠BDA逐渐变小;
故答案为:25°,115°,小;
(2)当DC=2时,△ABD≌△DCE,
理由:∵∠C=40°,
∴∠DEC+∠EDC=140°,
又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC,
又∵AB=DC=2,
∴△ABD≌△DCE(AAS),
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,
理由:∵∠BDA=110°时,
∴∠ADC=70°,
∵∠C=40°,
∴∠DAC=70°,∠AED=∠C+∠EDC=30°+40°=70°,
∴∠DAC=∠AED,
∴△ADE的形状是等腰三角形;
∵当∠BDA的度数为80°时,
∴∠ADC=100°,
∵∠C=40°,
∴∠DAC=40°,
∴∠DAC=∠ADE,
∴△ADE的形状是等腰三角形.
24.(1)证明:∵BD⊥AC,
∴∠BDC=90°,
∵∠ABC=90°,
∴∠ABD+∠DBC=90°,∠DBC+∠C=90°,
∴∠ABD=∠C,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠BGE=∠ABD+∠BAE,∠BEG=∠C+∠EAC,
∴∠BGE=∠BEG,
∴BG=BE,
∵BF⊥EG,
∴BF平分∠DBC.
(2)解:∵∠ABF=3∠C,∠ABD=∠C,BF平分∠DBC,
∴∠FBD=∠FBC=2∠C,
∴5∠C=90°,
∴∠C=18°.
25.解:(1)∵AB=AC,∠BAC=40°,
∴∠ABC=70°,
∵BE平分∠ABC,
∴∠ABF=35°,
∵AF⊥AB,
∴∠BAF=90°,
∴∠AFE=125°.
(2)∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵BD⊥AC,
∴∠ADB=CDB=90°,
∴△ABD≌△CBD(ASA),
∴AB=BC,
∵AB=AC,
∴三角形ABC是等边三角形,
∴∠ABF=30°,
∴AF=4,
在Rt△ADF中,
DF=2.
26.解:(1)当E为AB的中点时,AE=DB;
(2)AE=DB,理由如下,过点E作EF∥BC,交AC于点F,
证明:∵△ABC为等边三角形,
∴△AEF为等边三角形,
∴AE=EF,BE=CF,
∵ED=EC,
∴∠D=∠ECD,
∵∠DEB=60°﹣∠D,∠ECF=60°﹣∠ECD,
∴∠DEB=∠ECF,
在△DBE和△EFC中,
,
∴△DBE≌△EFC(SAS),
∴DB=EF,
则AE=DB;
(3)点E在AB延长线上时,如图所示,同理可得△DBE≌△EFC,
∴DB=EF=2,BC=1,
则CD=BC+DB=3.
故答案为:(1)=;(2)=
