第1章丰富的图形世界 能力提高训练 2021-2022学年鲁教版(五四制)六年级数学上册(word版含解析)
文档属性
| 名称 | 第1章丰富的图形世界 能力提高训练 2021-2022学年鲁教版(五四制)六年级数学上册(word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 237.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 22:08:57 | ||
图片预览



文档简介
2021-2022学年鲁教版六年级数学上册《第1章丰富的图形世界》能力提高训练(附答案)
一、选择题
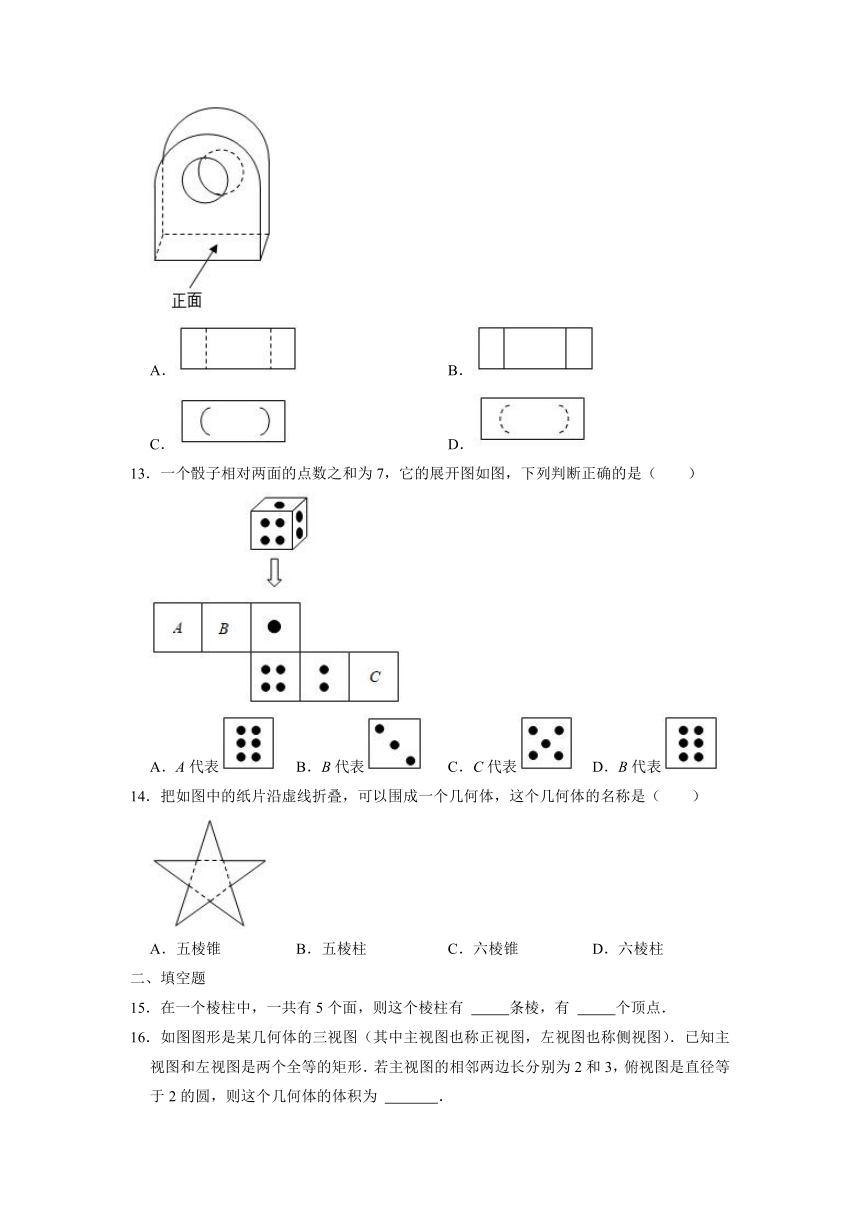
1.下列图形中不是正方体的表面展开图的是( )
A.
B.
C.
D.
2.某立体图形的表面展开图如图所示,这个立体图形是( )
A.
B.
C.
D.
3.用一个平面去截下列的几何体,可以得到长方形截面的几何体有( )
A.1个
B.2个
C.3个
D.4个
4.如图所示,将正方体纸盒的表面沿某些棱剪开,该正方体的展开图为( )
A.
B.
C.
D.
5.从上面看如图几何体得到的平面图形是( )
A.
B.
C.
D.
6.小明在一个正方体盒子的每个面上都写了一个字,正方体的平面展开图如图所示,那么在这个正方体盒子的表面与“祝”相对的面上所写的字是( )
A.考
B.试
C.成
D.功
7.某几何体的展开图如图所示,该几何体是( )
A.
B.
C.
D.
8.下列三棱柱展开图错误的是( )
A.
B.
C.
D.
9.甲和乙两个几何体都是由大小相同的小立方块搭成,它们的俯视图如图,小正方形中数字表示该位置上的小立方块个数,则下列说法中正确的是( )
A.甲和乙左视图相同,主视图相同
B.甲和乙左视图不相同,主视图不相同
C.甲和乙左视图相同,主视图不相同
D.甲和乙左视图不相同,主视图相同
10.如图所示的几何体是由5个大小相同的小正方体搭成的.其左视图是( )
A.
B.
C.
D.
11.下列四个正方体的展开图中,能折叠成如图所示的正方体的是( )
A.
B.
C.
D.
12.如图所示的几何体,其上半部有一个圆孔,则该几何体的俯视图是( )
A.
B.
C.
D.
13.一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )
A.A代表
B.B代表
C.C代表
D.B代表
14.把如图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )
A.五棱锥
B.五棱柱
C.六棱锥
D.六棱柱
二、填空题
15.在一个棱柱中,一共有5个面,则这个棱柱有
条棱,有
个顶点.
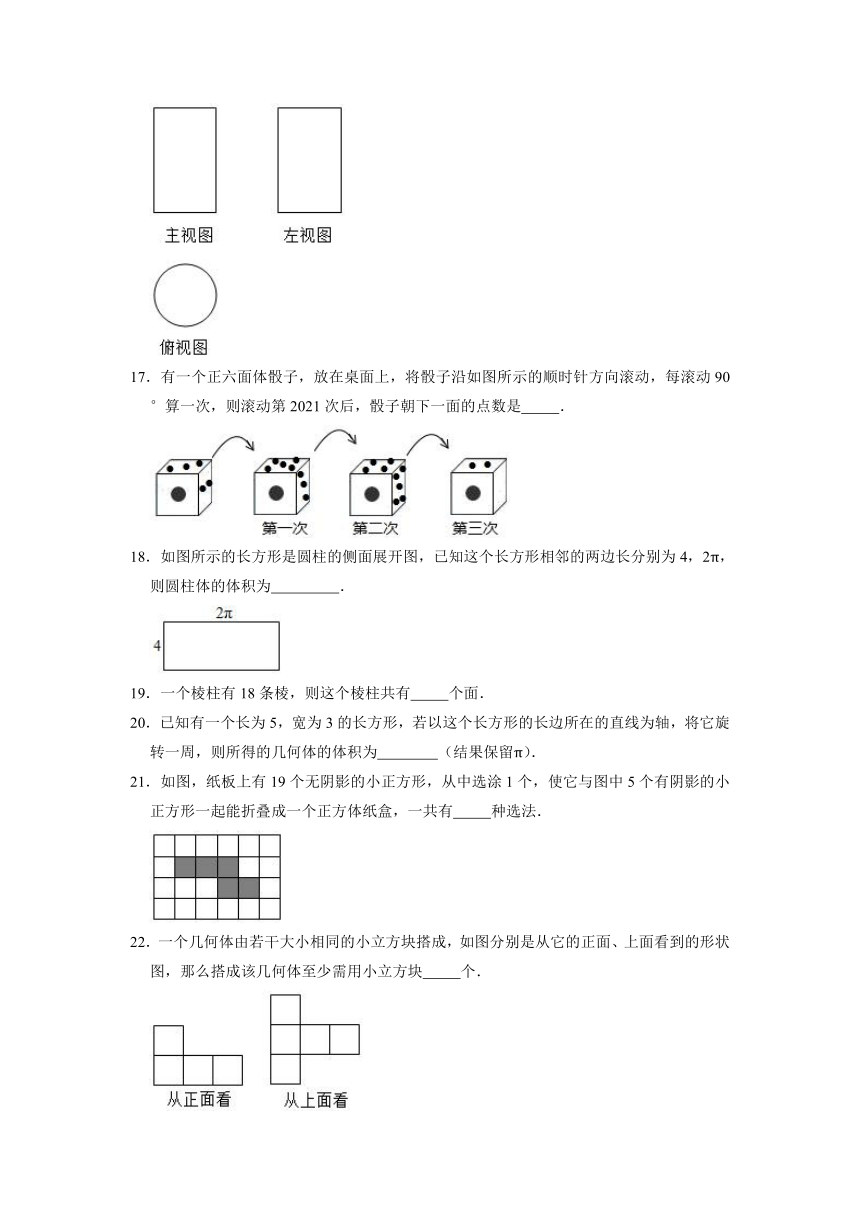
16.如图图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图).已知主视图和左视图是两个全等的矩形.若主视图的相邻两边长分别为2和3,俯视图是直径等于2的圆,则这个几何体的体积为
.
17.有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2021次后,骰子朝下一面的点数是
.
18.如图所示的长方形是圆柱的侧面展开图,已知这个长方形相邻的两边长分别为4,2π,则圆柱体的体积为
.
19.一个棱柱有18条棱,则这个棱柱共有
个面.
20.已知有一个长为5,宽为3的长方形,若以这个长方形的长边所在的直线为轴,将它旋转一周,则所得的几何体的体积为
(结果保留π).
21.如图,纸板上有19个无阴影的小正方形,从中选涂1个,使它与图中5个有阴影的小正方形一起能折叠成一个正方体纸盒,一共有
种选法.
22.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,那么搭成该几何体至少需用小立方块
个.
23.如图,将一个正方体截去一个角变成一个多面体,则这个多面体有
个顶点.
24.在一张桌子上摆放着一些碟子,从3个方向看到的3种视图如图所示,则这个桌子上的碟子共有
个.
25.如图,下列图形中,①能折叠成
,②能折叠成
,③能折叠成
.
26.如图,这是一个正方体的展开图,折叠后它们的相对两面的数字之和都相等,则x﹣y=
.
27.一个几何体从正面和上面看到的图形如图所示,若这个几何体最多有a个小正方体组成,最少有b个小正方体组成,则a+b=
.
28.有一个正方体的六个面上分别标有数字1、2、3、4、5、6,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字6的面所对面上的数字记为a,2的面所对面上数字记为b,那么2a+3b的值为
.
三、解答题
29.将一个长4cm,宽2cm的矩形绕它的一边所在的直线旋转一周,求所得几何体的侧面积.(结果中保留π)
30.如图,是一个几何体的表面展开图.
(1)该几何体是
.
A.正方体;B.长方体;C.三棱柱;D.四棱锥.
(2)依据图中数据求该几何体的体积.
31.把一根长1.5米的圆柱形钢材截成三段后,如图,表面积比原来增加8平方米,这根钢材原来的体积是多少?
32.如图是把一个圆柱纵向切开后的图形.
(1)图中有几个面?有几个平面和曲面?
(2)图中有几条线?它们是直线还是曲线?
(3)图中线与线之间一共交成多少个点?
33.如图是由若干个相同的正方体组成的一个立体图形从三个不同方向看到的形状图,根据形状图回答下列问题:
(1)原立体图形共有几层?(2)立体图形中共有多少个小正方体?
34.已知一个直棱柱有8个面,它的底面边长都是5cm,侧棱长都是4cm.
(1)它是几棱柱?它有多少个顶点?多少条棱?
(2)这个棱柱的所有侧面的面积之和是多少?
35.聪聪在学习了“展开与折叠”这一课后,明白了很多几何体都能展开成平面图形,于是他在家用剪刀把一个长方体纸盒(如图(1))剪开了,可是他一不小心多剪了一条棱,把纸盒剪成了两部分,即图(2)中的①和②.根据你所学的知识,回答下列问题:
(1)若这个长方体纸盒的长、宽、高分别是8cm,4cm,2cm,则该长方体纸盒的体积是多少?
(2)聪聪一共剪开了
条棱;
(3)现在聪聪想将剪掉的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪掉的②粘贴到①中的什么位置?请你帮助他在①上补全一种情况.
36.如图,是由6个大小相同的小立方体块搭建的几何体,其中每个小正方体的棱长为1厘米.
(1)直接写出这个几何体的表面积(包括底部):
;
(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
参考答案
1.解:由正方体四个侧面和上下两个底面的特征可知,A,C,D选项可以拼成一个正方体,而B选项,上底面不可能有两个,故不是正方体的展开图,
故选:B.
2.解:四个三角形和一个四边形,是四棱锥的组成,所以该立体图形的名称为四棱锥.
故选:A.
3.解:球、圆锥不可能得到长方形截面,
故能得到长方形截面的几何体有:圆柱、三棱柱,一共有2个.
故选:B.
4.解:A、把展开图折叠,当圆在前面时,角在上面且开口对着圆,等号在右面,故此选项符合题意;
B、把展开图折叠,当圆在前面时,角在左面且开口对着圆,等号在右面,故此选项不符合题意;
C、把展开图折叠,当圆在前面时,角在上面且开口不对着圆,等号在右面,故此选项不符合题意;
D、把展开图折叠,当圆在前面时,角在下面且开口不对着圆,等号在右面,故此选项不符合题意.
故选:A.
5.解:从上面看如图几何体得到的平面图形为:
故选:A.
6.解:根据正方体表面展开图的“相间、Z端是对面”可知,
“祝”与“成”是对面,
“你”与“试”是对面,
“考”与“功”是对面,
故选:C.
7.解:扇形和圆折叠后,能围成的几何体是圆锥.
故选:D.
8.解:A、B、C中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.D围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故D不能围成三棱柱.
故选:D.
9.解:∵甲、乙都是由5个大小相同的小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,
∴甲和乙的主视图均为3列,立方体的个数从左到右分别是1,2,1,
∴主视图相同,
甲的左视图是有两列,正方形的个数分别是2,1,
乙的左视图也是两列,但正方形的个数分别为1,2,
故主视图相同、左视图不同.
故选:D.
10.解:从左边看,底层是三个小正方形,上层的中间是一个小正方形,
故选:A.
11.解:由正方体图,得
A面、B面、C面是邻面,故B符合题意,
故选:B.
12.解:从上面看该几何体,能看见的轮廓线用实线表示,看不见的轮廓线用虚线表示,因此所看到的图形与选项A中的图形相同,
故选:A.
13.解:根据正方体的表面展开图,相对的面之间一定相隔一个正方形,
A与点数是1的对面,B与点数是2的对面,C与点数是4的对面,
∵骰子相对两面的点数之和为7,
∴A代表的点数是6,B代表的点数是5,C代表的点数是3.
故选:A.
14.解:由图可知:折叠后,该几何体的底面是五边形,
则该几何体为五棱锥,
故选:A.
15.解:一个棱柱中,一共有5个面,则有2个底面,3个侧面,因此此立体图形是三棱柱,则这个棱柱棱的条数有9条,有6个顶点.
故答案为:9;6.
16.解:由三视图知几何体为圆柱,
且底面圆的半径是1,高是3,
∴这个几何体的体积为:π×12×3=3π.
故答案为:3π.
17.解:观察图形知道点数三和点数四相对,点数二和点数五相对且滚动四次一循环,
∵2021÷4=505…1,
∴滚动第2021次后与第1次相同,
∴朝下的数字是5的对面2,
故答案为:2.
18.解:①以2π为底面周长,4为高,
此时圆柱体的底面半径为=1,
∴圆柱体的体积为π×12×4=4π,
②以4为圆柱体的底面周长,2π为高,
此时圆柱体的底面半径为,
∴圆柱体的体积为π×()2×2π=8,
故答案为:4π或8.
19.解:由n棱柱有3n条棱,
所以一个棱柱有18条棱,则它是18÷3=6,因此它是六棱柱,
而六棱柱有6+2=8个面,
故答案为:八.
20.解:长方形绕一边旋转一周,得圆柱,所得的几何体的体积为:π×32×5=45π.
故答案为:45π.
21.解:如图所示:共四种.
故答案为:4.
22.解:根据主视图可得,俯视图中第一列中至少一处有2层;
所以该几何体至少是用6个小立方块搭成的.
故答案为:6.
23.解:正方体有8个顶点,将这个正方体按照如图所示的方式截去一个角后,
所得到的多面体的顶点数为8﹣1+3=10,
故答案为:10.
24.解:易得三摞碟子数从左往右分别为5,4,3,
则这个桌子上共有5+4+3=12个碟子.
故答案为:12.
25.解:①能折叠成圆柱,②能折叠成棱柱,③能折叠成圆锥.
故答案为:圆柱,棱柱,圆锥.
26.解:根据正方体表面展开图的“相间、Z端是对面”可得,
“x”与“3x”的面是相对的,
“2”与“6”的面是相对的,
“y﹣1”与“5”的面是相对的,
又因为相对两面的数字之和都相等,
所以x+3x=2+6=y﹣1+5,
解得x=2,y=4,
所以x﹣y=2﹣4=﹣2,
故答案为:﹣2.
27.解:结合主视图和俯视图可知,左边后排最多有3个,左边前排最多有3个,右边只有一层,且只有1个,
所以图中的小正方体最多7块,
结合主视图和俯视图可知,左边后排最少有1个,左边前排最多有3个,右边只有一层,且只有1个,
所以图中的小正方体最少5块,
a+b=7+5=12.
故答案为:12.
28.解:由三个正方体上所标的数字可得,
“1”的邻面有“6,4,2,3”,因此“1”对“5”,
“3”的邻面有“1,2,4,5”,因此“3”对“6”,
于是“2”对“4”,
∵标有数字6的面所对面上的数字记为a,2的面所对面上数字记为b,
∴a=3,b=4,
∴2a+3b=6+12=18.
29.解:矩形绕它的一边所在的直线旋转一周,所得几何体为圆柱,
若以长边所在直线旋转一周,则形成的圆柱的底面半径为2cm,高为4cm,
∴该圆柱的侧面积为2π×2×4=16π,
若以宽边所在直线旋转一周,则形成的圆柱的底面半径为4cm,高为2cm,
∴该圆柱的侧面积为2π×4×2=16π,
∴所得几何体的侧面积为16π.
30.解:(1)由图得,这个几何体为长方体.
故答案为:B.
(2)3×2×1=6(米3),
答:该几何体的体积是6米3.
31.解:8÷4=2(平方米),
2×1.5=3(立方米).
答:这根钢材原来的体积为3立方米.
32.解:(1)图中有4个面,有3个平面,1个曲面;
(2)图中有6条线,它们是4条直线,2条曲线;
(3)图中线与线之间一共交成4个点.
33.解:(1)由三视图可得,原立体图形共有2层;
(2)该立体图形共有2摞小正方体组成,
由俯视图我们可知,第1摞有4个小正方体,
由主视图和左视图我们可知,第2摞有一个小正方体,
故这些相同的小正方体共有5个.
34.解:因为一个直棱柱有8个面,所以它是六棱柱,
所以有12个顶点,18条棱,
答:它是六棱柱,它有12个顶点,18条棱;
(2)因为六棱柱的底面边长都是5cm,侧棱长都是4cm.
所以侧面展开后是长为5×6=30cm,宽为4cm的长方形,
因此侧面积为30×4=120(cm2),
答:这个棱柱的所有侧面的面积之和是120cm2.
35.解:(1)8×4×2=64(cm3)
该长方体纸盒的体积是64cm3;
(2)聪聪一共剪开了8条棱.
故答案为:8;
(3)如图,就是所画的图形(答案不唯一,有以下四种情况供参考).
36.解:(1)(5+4+4)×2=26(cm2),
故答案为:26cm2;
(2)根据三视图的画法,画出相应的图形如下:
一、选择题
1.下列图形中不是正方体的表面展开图的是( )
A.
B.
C.
D.
2.某立体图形的表面展开图如图所示,这个立体图形是( )
A.
B.
C.
D.
3.用一个平面去截下列的几何体,可以得到长方形截面的几何体有( )
A.1个
B.2个
C.3个
D.4个
4.如图所示,将正方体纸盒的表面沿某些棱剪开,该正方体的展开图为( )
A.
B.
C.
D.
5.从上面看如图几何体得到的平面图形是( )
A.
B.
C.
D.
6.小明在一个正方体盒子的每个面上都写了一个字,正方体的平面展开图如图所示,那么在这个正方体盒子的表面与“祝”相对的面上所写的字是( )
A.考
B.试
C.成
D.功
7.某几何体的展开图如图所示,该几何体是( )
A.
B.
C.
D.
8.下列三棱柱展开图错误的是( )
A.
B.
C.
D.
9.甲和乙两个几何体都是由大小相同的小立方块搭成,它们的俯视图如图,小正方形中数字表示该位置上的小立方块个数,则下列说法中正确的是( )
A.甲和乙左视图相同,主视图相同
B.甲和乙左视图不相同,主视图不相同
C.甲和乙左视图相同,主视图不相同
D.甲和乙左视图不相同,主视图相同
10.如图所示的几何体是由5个大小相同的小正方体搭成的.其左视图是( )
A.
B.
C.
D.
11.下列四个正方体的展开图中,能折叠成如图所示的正方体的是( )
A.
B.
C.
D.
12.如图所示的几何体,其上半部有一个圆孔,则该几何体的俯视图是( )
A.
B.
C.
D.
13.一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )
A.A代表
B.B代表
C.C代表
D.B代表
14.把如图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )
A.五棱锥
B.五棱柱
C.六棱锥
D.六棱柱
二、填空题
15.在一个棱柱中,一共有5个面,则这个棱柱有
条棱,有
个顶点.
16.如图图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图).已知主视图和左视图是两个全等的矩形.若主视图的相邻两边长分别为2和3,俯视图是直径等于2的圆,则这个几何体的体积为
.
17.有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2021次后,骰子朝下一面的点数是
.
18.如图所示的长方形是圆柱的侧面展开图,已知这个长方形相邻的两边长分别为4,2π,则圆柱体的体积为
.
19.一个棱柱有18条棱,则这个棱柱共有
个面.
20.已知有一个长为5,宽为3的长方形,若以这个长方形的长边所在的直线为轴,将它旋转一周,则所得的几何体的体积为
(结果保留π).
21.如图,纸板上有19个无阴影的小正方形,从中选涂1个,使它与图中5个有阴影的小正方形一起能折叠成一个正方体纸盒,一共有
种选法.
22.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,那么搭成该几何体至少需用小立方块
个.
23.如图,将一个正方体截去一个角变成一个多面体,则这个多面体有
个顶点.
24.在一张桌子上摆放着一些碟子,从3个方向看到的3种视图如图所示,则这个桌子上的碟子共有
个.
25.如图,下列图形中,①能折叠成
,②能折叠成
,③能折叠成
.
26.如图,这是一个正方体的展开图,折叠后它们的相对两面的数字之和都相等,则x﹣y=
.
27.一个几何体从正面和上面看到的图形如图所示,若这个几何体最多有a个小正方体组成,最少有b个小正方体组成,则a+b=
.
28.有一个正方体的六个面上分别标有数字1、2、3、4、5、6,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字6的面所对面上的数字记为a,2的面所对面上数字记为b,那么2a+3b的值为
.
三、解答题
29.将一个长4cm,宽2cm的矩形绕它的一边所在的直线旋转一周,求所得几何体的侧面积.(结果中保留π)
30.如图,是一个几何体的表面展开图.
(1)该几何体是
.
A.正方体;B.长方体;C.三棱柱;D.四棱锥.
(2)依据图中数据求该几何体的体积.
31.把一根长1.5米的圆柱形钢材截成三段后,如图,表面积比原来增加8平方米,这根钢材原来的体积是多少?
32.如图是把一个圆柱纵向切开后的图形.
(1)图中有几个面?有几个平面和曲面?
(2)图中有几条线?它们是直线还是曲线?
(3)图中线与线之间一共交成多少个点?
33.如图是由若干个相同的正方体组成的一个立体图形从三个不同方向看到的形状图,根据形状图回答下列问题:
(1)原立体图形共有几层?(2)立体图形中共有多少个小正方体?
34.已知一个直棱柱有8个面,它的底面边长都是5cm,侧棱长都是4cm.
(1)它是几棱柱?它有多少个顶点?多少条棱?
(2)这个棱柱的所有侧面的面积之和是多少?
35.聪聪在学习了“展开与折叠”这一课后,明白了很多几何体都能展开成平面图形,于是他在家用剪刀把一个长方体纸盒(如图(1))剪开了,可是他一不小心多剪了一条棱,把纸盒剪成了两部分,即图(2)中的①和②.根据你所学的知识,回答下列问题:
(1)若这个长方体纸盒的长、宽、高分别是8cm,4cm,2cm,则该长方体纸盒的体积是多少?
(2)聪聪一共剪开了
条棱;
(3)现在聪聪想将剪掉的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪掉的②粘贴到①中的什么位置?请你帮助他在①上补全一种情况.
36.如图,是由6个大小相同的小立方体块搭建的几何体,其中每个小正方体的棱长为1厘米.
(1)直接写出这个几何体的表面积(包括底部):
;
(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
参考答案
1.解:由正方体四个侧面和上下两个底面的特征可知,A,C,D选项可以拼成一个正方体,而B选项,上底面不可能有两个,故不是正方体的展开图,
故选:B.
2.解:四个三角形和一个四边形,是四棱锥的组成,所以该立体图形的名称为四棱锥.
故选:A.
3.解:球、圆锥不可能得到长方形截面,
故能得到长方形截面的几何体有:圆柱、三棱柱,一共有2个.
故选:B.
4.解:A、把展开图折叠,当圆在前面时,角在上面且开口对着圆,等号在右面,故此选项符合题意;
B、把展开图折叠,当圆在前面时,角在左面且开口对着圆,等号在右面,故此选项不符合题意;
C、把展开图折叠,当圆在前面时,角在上面且开口不对着圆,等号在右面,故此选项不符合题意;
D、把展开图折叠,当圆在前面时,角在下面且开口不对着圆,等号在右面,故此选项不符合题意.
故选:A.
5.解:从上面看如图几何体得到的平面图形为:
故选:A.
6.解:根据正方体表面展开图的“相间、Z端是对面”可知,
“祝”与“成”是对面,
“你”与“试”是对面,
“考”与“功”是对面,
故选:C.
7.解:扇形和圆折叠后,能围成的几何体是圆锥.
故选:D.
8.解:A、B、C中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.D围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故D不能围成三棱柱.
故选:D.
9.解:∵甲、乙都是由5个大小相同的小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,
∴甲和乙的主视图均为3列,立方体的个数从左到右分别是1,2,1,
∴主视图相同,
甲的左视图是有两列,正方形的个数分别是2,1,
乙的左视图也是两列,但正方形的个数分别为1,2,
故主视图相同、左视图不同.
故选:D.
10.解:从左边看,底层是三个小正方形,上层的中间是一个小正方形,
故选:A.
11.解:由正方体图,得
A面、B面、C面是邻面,故B符合题意,
故选:B.
12.解:从上面看该几何体,能看见的轮廓线用实线表示,看不见的轮廓线用虚线表示,因此所看到的图形与选项A中的图形相同,
故选:A.
13.解:根据正方体的表面展开图,相对的面之间一定相隔一个正方形,
A与点数是1的对面,B与点数是2的对面,C与点数是4的对面,
∵骰子相对两面的点数之和为7,
∴A代表的点数是6,B代表的点数是5,C代表的点数是3.
故选:A.
14.解:由图可知:折叠后,该几何体的底面是五边形,
则该几何体为五棱锥,
故选:A.
15.解:一个棱柱中,一共有5个面,则有2个底面,3个侧面,因此此立体图形是三棱柱,则这个棱柱棱的条数有9条,有6个顶点.
故答案为:9;6.
16.解:由三视图知几何体为圆柱,
且底面圆的半径是1,高是3,
∴这个几何体的体积为:π×12×3=3π.
故答案为:3π.
17.解:观察图形知道点数三和点数四相对,点数二和点数五相对且滚动四次一循环,
∵2021÷4=505…1,
∴滚动第2021次后与第1次相同,
∴朝下的数字是5的对面2,
故答案为:2.
18.解:①以2π为底面周长,4为高,
此时圆柱体的底面半径为=1,
∴圆柱体的体积为π×12×4=4π,
②以4为圆柱体的底面周长,2π为高,
此时圆柱体的底面半径为,
∴圆柱体的体积为π×()2×2π=8,
故答案为:4π或8.
19.解:由n棱柱有3n条棱,
所以一个棱柱有18条棱,则它是18÷3=6,因此它是六棱柱,
而六棱柱有6+2=8个面,
故答案为:八.
20.解:长方形绕一边旋转一周,得圆柱,所得的几何体的体积为:π×32×5=45π.
故答案为:45π.
21.解:如图所示:共四种.
故答案为:4.
22.解:根据主视图可得,俯视图中第一列中至少一处有2层;
所以该几何体至少是用6个小立方块搭成的.
故答案为:6.
23.解:正方体有8个顶点,将这个正方体按照如图所示的方式截去一个角后,
所得到的多面体的顶点数为8﹣1+3=10,
故答案为:10.
24.解:易得三摞碟子数从左往右分别为5,4,3,
则这个桌子上共有5+4+3=12个碟子.
故答案为:12.
25.解:①能折叠成圆柱,②能折叠成棱柱,③能折叠成圆锥.
故答案为:圆柱,棱柱,圆锥.
26.解:根据正方体表面展开图的“相间、Z端是对面”可得,
“x”与“3x”的面是相对的,
“2”与“6”的面是相对的,
“y﹣1”与“5”的面是相对的,
又因为相对两面的数字之和都相等,
所以x+3x=2+6=y﹣1+5,
解得x=2,y=4,
所以x﹣y=2﹣4=﹣2,
故答案为:﹣2.
27.解:结合主视图和俯视图可知,左边后排最多有3个,左边前排最多有3个,右边只有一层,且只有1个,
所以图中的小正方体最多7块,
结合主视图和俯视图可知,左边后排最少有1个,左边前排最多有3个,右边只有一层,且只有1个,
所以图中的小正方体最少5块,
a+b=7+5=12.
故答案为:12.
28.解:由三个正方体上所标的数字可得,
“1”的邻面有“6,4,2,3”,因此“1”对“5”,
“3”的邻面有“1,2,4,5”,因此“3”对“6”,
于是“2”对“4”,
∵标有数字6的面所对面上的数字记为a,2的面所对面上数字记为b,
∴a=3,b=4,
∴2a+3b=6+12=18.
29.解:矩形绕它的一边所在的直线旋转一周,所得几何体为圆柱,
若以长边所在直线旋转一周,则形成的圆柱的底面半径为2cm,高为4cm,
∴该圆柱的侧面积为2π×2×4=16π,
若以宽边所在直线旋转一周,则形成的圆柱的底面半径为4cm,高为2cm,
∴该圆柱的侧面积为2π×4×2=16π,
∴所得几何体的侧面积为16π.
30.解:(1)由图得,这个几何体为长方体.
故答案为:B.
(2)3×2×1=6(米3),
答:该几何体的体积是6米3.
31.解:8÷4=2(平方米),
2×1.5=3(立方米).
答:这根钢材原来的体积为3立方米.
32.解:(1)图中有4个面,有3个平面,1个曲面;
(2)图中有6条线,它们是4条直线,2条曲线;
(3)图中线与线之间一共交成4个点.
33.解:(1)由三视图可得,原立体图形共有2层;
(2)该立体图形共有2摞小正方体组成,
由俯视图我们可知,第1摞有4个小正方体,
由主视图和左视图我们可知,第2摞有一个小正方体,
故这些相同的小正方体共有5个.
34.解:因为一个直棱柱有8个面,所以它是六棱柱,
所以有12个顶点,18条棱,
答:它是六棱柱,它有12个顶点,18条棱;
(2)因为六棱柱的底面边长都是5cm,侧棱长都是4cm.
所以侧面展开后是长为5×6=30cm,宽为4cm的长方形,
因此侧面积为30×4=120(cm2),
答:这个棱柱的所有侧面的面积之和是120cm2.
35.解:(1)8×4×2=64(cm3)
该长方体纸盒的体积是64cm3;
(2)聪聪一共剪开了8条棱.
故答案为:8;
(3)如图,就是所画的图形(答案不唯一,有以下四种情况供参考).
36.解:(1)(5+4+4)×2=26(cm2),
故答案为:26cm2;
(2)根据三视图的画法,画出相应的图形如下:
