八年级数学用函数图象解不等式

(共17张PPT)
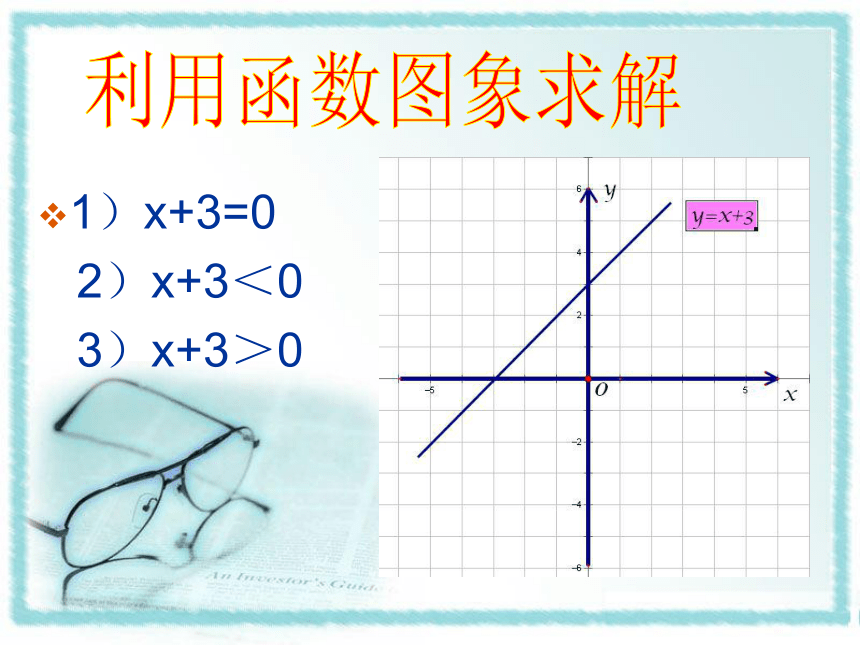
1）x+3=0
2）x+3＜0
3）x+3＞0
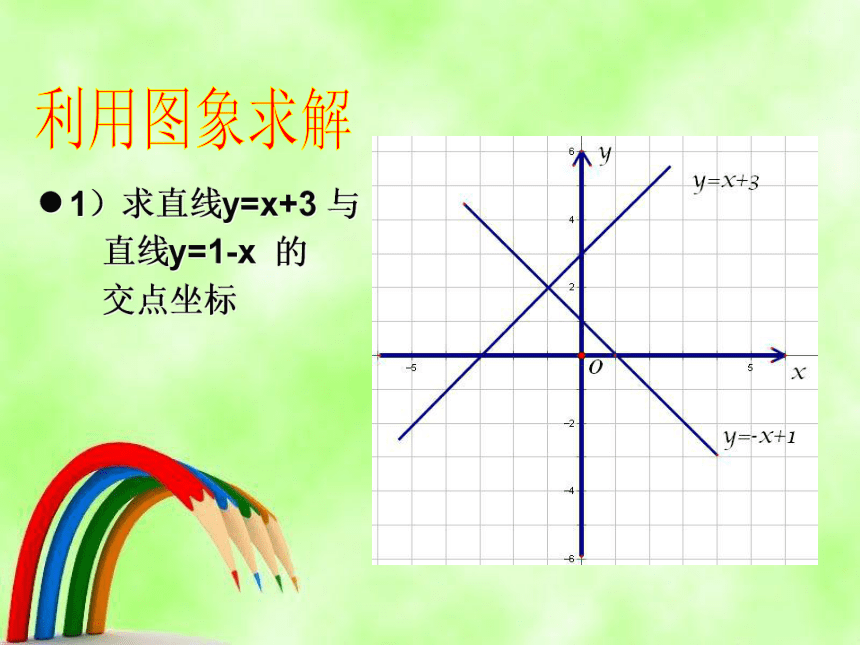
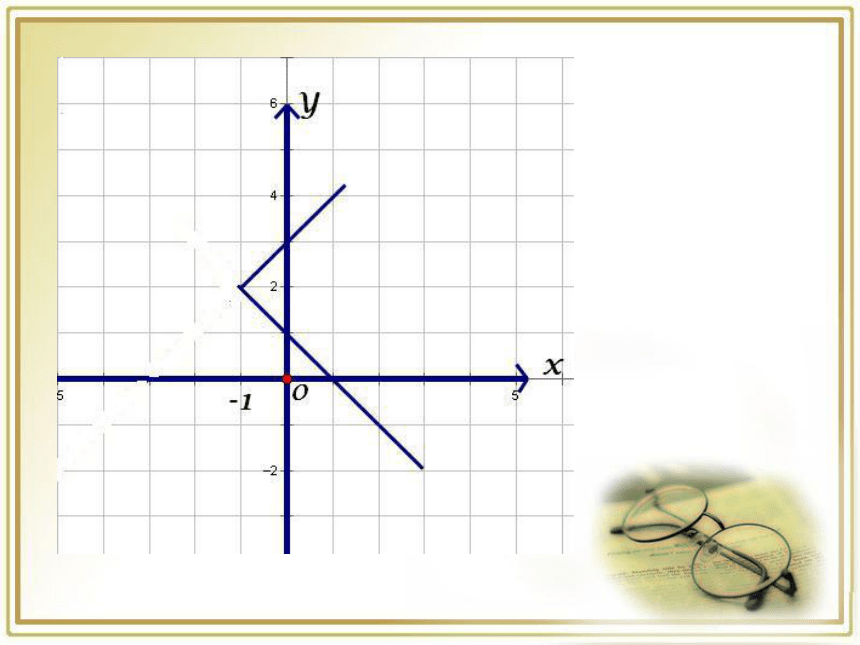
1）求直线y=x+3 与
直线y=1-x 的
交点坐标
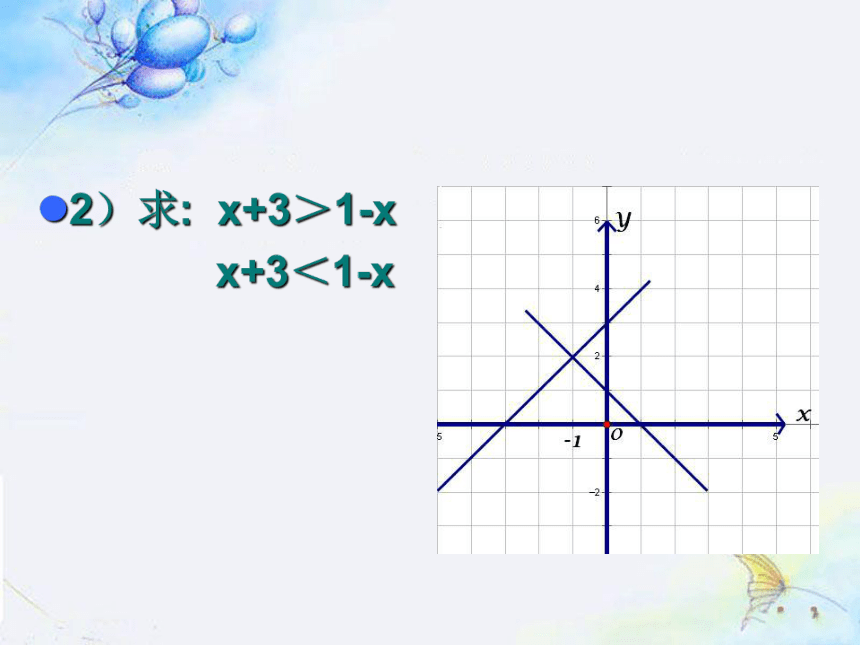
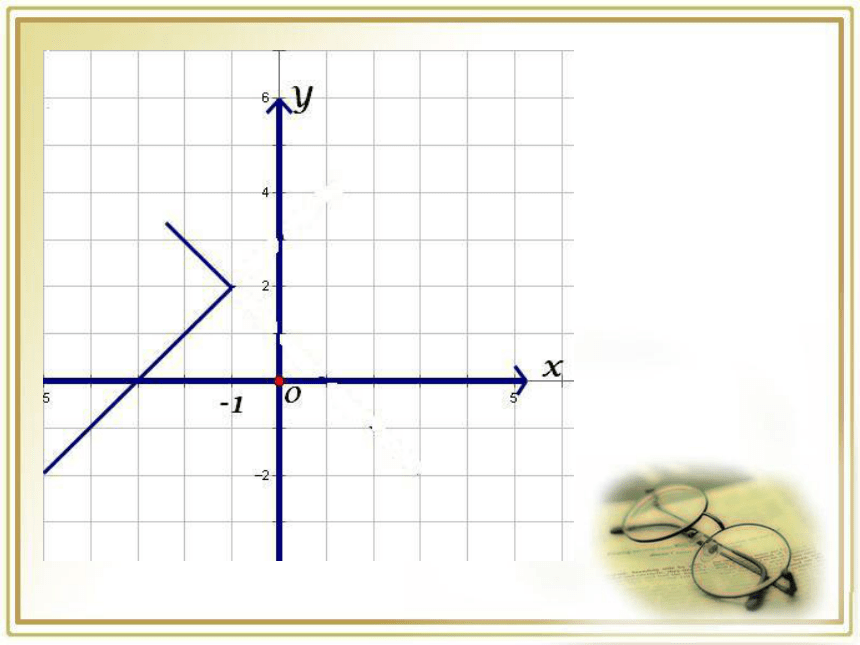
2）求: x+3＞1-x
x+3＜1-x
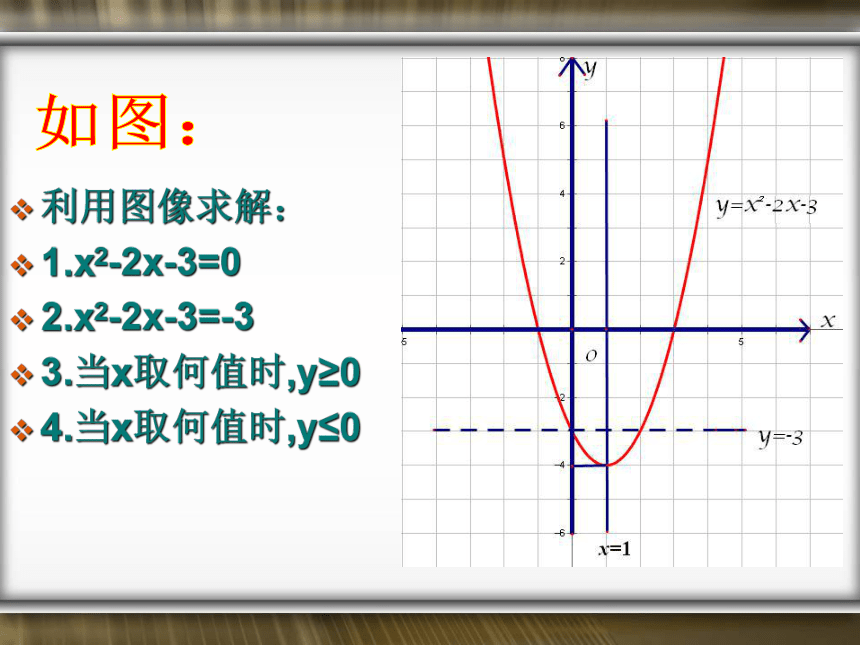
利用图像求解：
1.x2-2x-3=0
2.x2-2x-3=-3
3.当x取何值时,y≥0
4.当x取何值时,y≤0
应用解决：
利用一堵墙和10长的篱笆围成一矩形，如图：
1.如何围能使矩形的面积为12平方米？
2.如何围才能使矩形的面积最大？
3.如果墙的长度可用的只有4米，则为矩形最大面积是多少？
学以致用
1利用图像求解：
⑴直接写出方程4-2x=0的解
⑵当x____时，y1＞0
⑶当x＞1时，y1___y2
当x＜1时 4-2x____3-x
y
x
2）一家电信公司给顾客提供两种上网收费方式：方式A以每分0.1元的价格按上网所用时间计费；方式B除收月基本费20元外，再以每分0.05元的价格上网所用时间计费。若上网所用时间为x分，计费为 y分（如图所示），是在同一坐标系中，分别描述两种计费方式的函数的图像，你通过观察发现用哪种方式上网省钱？
3）观察图像。若
x2＜- x+3时，
则自变量x的取值范围是多少？
1.已知A(-4，n), B(2，-4)是一次函数y=kx+b与反比例
函数y= 的图像的两个交点，
⑴求反比例函数和一次函数的解析式。
⑵求方程kx+b- =0的解
⑶求不等式kx+b＜ 的解集
2、某校组织340名学生进行长途考察活动，带有行李170件，计划租用甲、乙两种型号的汽车共10辆，经过了解，甲车每辆最多能载40人和16件行李，乙车每辆最多能载30人和20件行李。
⑴请你帮学校设计所有可行的租车方案。
⑵如果甲车的租金为每辆2000元，乙车的租金为每辆1800元，问哪种可行方案租车费用最省？