苏科版七年级数学上册2.4 绝对值与相反数课件(42张PPT)
文档属性
| 名称 | 苏科版七年级数学上册2.4 绝对值与相反数课件(42张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 00:00:00 | ||
图片预览









文档简介
(共42张PPT)
绝对值与相反数
学校
小明家
小丽家
假如他们都步行上学,且速度相同,谁花的时间更少些呢?
3
km
2
km
小丽
学校
小明家
小丽家
3
km
2
km
A
B
数轴上表示一个数的点与原点的距离,叫做这个数的绝对值.
3
2
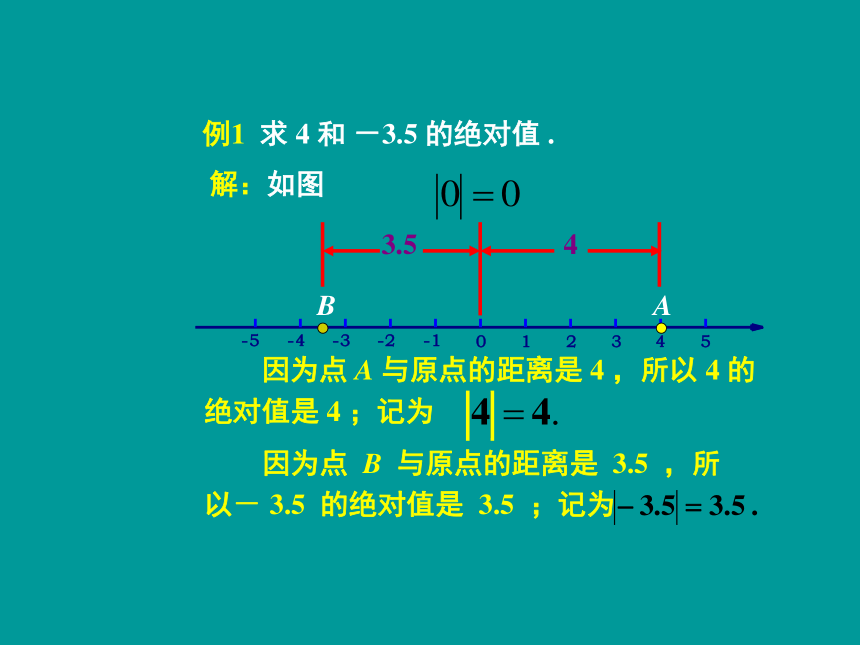
例1
求
4
和
-3.5
的绝对值
.
解:如图
A
B
4
3.5
因为点
A
与原点的距离是
4
,所以
4
的绝对值是
4
;记为
因为点
B
与原点的距离是
3.5
,所以-
3.5
的绝对值是
3.5
;记为
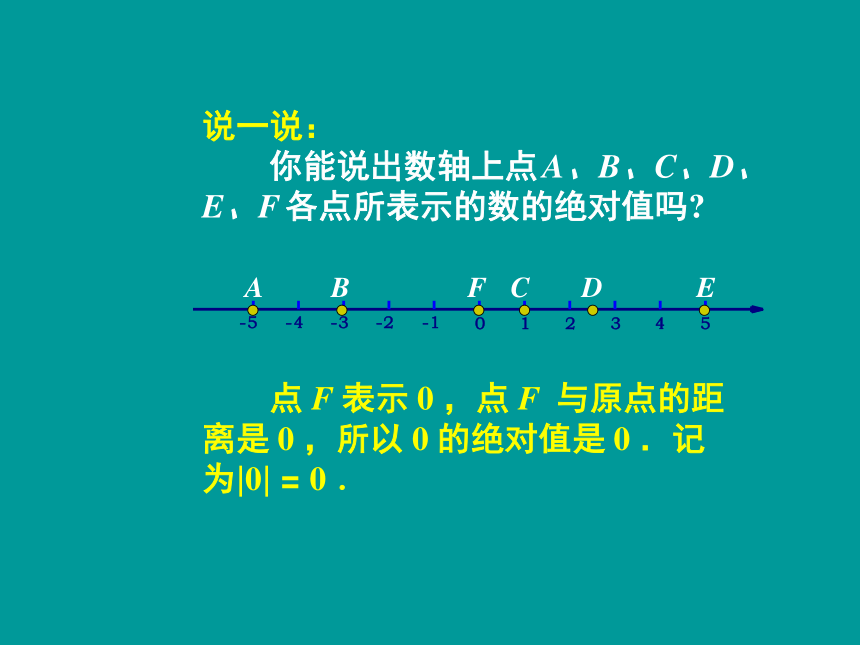
说一说:
你能说出数轴上点
A、B、C、D、E、F
各点所表示的数的绝对值吗?
点
A
表示
-5
,点
A
与原点的距离是
5
,所以
-5
的绝对值是
5
.记为|-5|
=
5.
B
F
E
D
C
A
点
B
表示
-3
,点
B
与原点的
距离是
3
,所以
-3
的绝对值是
3.
记为|-3|
=
3.
B
F
E
D
C
A
说一说:
你能说出数轴上点
A、B、C、D、E、F
各点所表示的数的绝对值吗?
点
C
表示
1
,点
C
与原点的距离是
1
,所以
1
的绝对值是
1.记为|1|
=
1.
B
F
E
D
C
A
说一说:
你能说出数轴上点
A、B、C、D、E、F
各点所表示的数的绝对值吗?
点
D
表示
2.5
,点
D
与原点的距离是
2.5
,所以
2.5
的绝对值是
2.5
.记为|2.5|
=
2.5.
B
F
E
D
C
A
说一说:
你能说出数轴上点
A、B、C、D、E、F
各点所表示的数的绝对值吗?
点
E
表示
5
,点
E
与原点的距
离是
5
,所以
5
的绝对值是
5.记为
|2.5|
=
2.5.
B
F
E
D
C
A
说一说:
你能说出数轴上点
A、B、C、D、E、F
各点所表示的数的绝对值吗?
点
F
表示
0
,点
F
与原点的距离是
0
,所以
0
的绝对值是
0
.记为|0|
=
0
.
B
F
E
D
C
A
说一说:
你能说出数轴上点
A、B、C、D、E、F
各点所表示的数的绝对值吗?
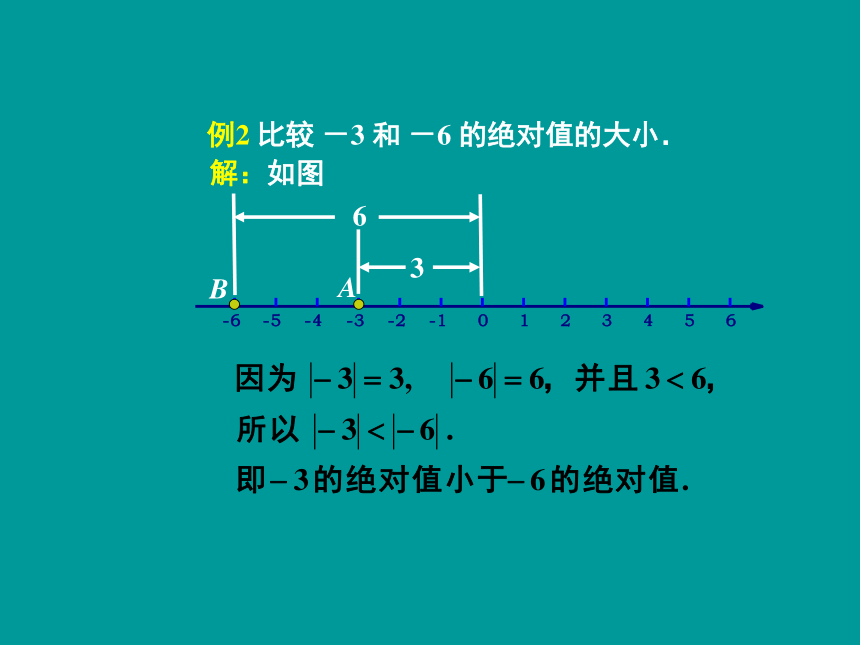
例2
比较
-3
和
-6
的绝对值的大小.
解:如图
A
B
3
6
先求出下列各式的值,再说出它们所表示的意义.
练一练
先求出下列各式的值,再说出它们所表示的意义.
练一练
你认为“任意有理数的绝对值都是正数”的说法正确吗?
任意一个有理数的绝对值是非负数.
比较下列各对数的大小:
练一练
动脑筋
有一天,甲、乙两个数在比谁
大.甲抢着说:“在数轴上我表示
的点到原点的距离比你表示的点到
原点的距离要大,看来我比你大”,
乙不甘示弱,紧接着说,“我是正
数,我大于零,也大于一切负数,
当然是我比你大”.你们说到底谁
大呢?
乙
甲
乙
甲
若甲是正数,由于甲表示的点到原点的距离比乙表示的点到原点的距离要大,所以甲比乙大;
若甲是负数,则显然乙比甲大.
B
D
C
A
C
、
D
两点到原点的距离相等,都等于3.
C
、
D
两点在原点的两侧,分别表示
-3
和
3
;
如图,观察数轴上
A、B
两点位置及其到原点的距离,你有什么发现?
5
5
3
3
A
、
B
两点在原点两侧,分别表示
-5
和
5
;
A
、
B
两点到原点的距离相等,都等于5.
D
C
A
B
E
F
G
H
例如:
E、F
两点分别表示
-2.5
和
2.5
;
5
5
与
3
3
2.5
2.5
-
与
与
与
观察下列
(+)
(+)
(+)
(+)
-
-
-
除
0
以外,任意一个有理数都由符号和绝对值两部分组成.
符号不同
绝对值相等
有理数,你有什么发现?
四对
-4.5
(
)
解:3的相反数是-3,
-4.5
的相反数是
4.5
,
例1
-
=
4.5
例2
解:
试一试:
化简―[―(+3.2)]
解:因为
+3.2
的相反数是
―3.2
,
所以
―(+3.2)=
―3.2
;
又因为
―3.2
的相反数是
3.2
,
所以
―[―(+3.2)]=
3.2
.
想一想:
请同学们仔细观察这五个等式,它们的符号变化有什么规律?
把一个数的多重符号化成单一符号时,若该数前面有奇数个“―”号,则化简的结果是负;
若该数前面有偶数个“―”号,则化简的结果是正.
-7
(1)-2的相反数是
,
3.75与
互为相反数,
相反数是其本身的数是
;
练一练:填空
(2)-(+7)=
,
-(-7)=
,
-[+(-7)]=
,
-[-(-7)]=
;
2
-3.75
0
-7
7
7
(3)判断下列语句,正确的是
.
①
―5
是相反数;
②
―5
与
+3
互为相反数;
③
―5
是
5
的相反数;
④
―5
和
5
互为相反数;
⑤
0
的相反数还是
0
.
③④⑤
(1)下列说法正确的是
(
)
A.正数的相反数是负数;
B.符号不同的两个数互为相反数;
C.π的相反数是
―3.14;
D.任何一个有理数都有相反数.
选择:
D
(2)一个数的相反数是非正数,那么这
个数一定是
(
)
A.正数
B.负数
C.零或正数
D.零
C
画一画:
在数轴上画出表示下列各数以及它们的相反数的点:
解:如图
A
B
C
D
A’
B’
(C’)
D’
如果改变有理数的符号,那么数轴上表示有理数的点的位置将会发生怎样的变化?
A
B
C
D
A’
B’
(C’)
D’
除
0
外,如果改变有理数的符号,那么数轴上表示有理数的点就从原点的一侧变到另一侧.
动脑筋:
如果数轴上两点
A、B
所表示的数互为相反数,点
A
在原点左侧,且
A、B
两点距离为
8
,你知道点
B
代表什么数吗?
答:点
B
代表
4
.
根据绝对值与相反数的意义填空:
(1)|2.3|=____,
|7/4|=_____,
|6|=_____
(2)|-5|=____,
|-10.5|=____,
|-7/4|=_____,
-5的相反数是___,-10.5的相反数是_____,
-7/4的相反数是_____,
(3)0的绝对值是____,0的相反数是_____
思考:一个数的绝对值与这个数本身、或与它的相反数之间有什么关系?你发现了什么?
2.3
7/4
10.5
5
5
6
7/4
0
10.5
7/4
0
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0
的绝对值是0.
归纳总结
符号表示
,
,
,
互为相反数的两个数的绝对值相等
互为相反数的两个数的绝对值有什么关系?
比较大小法则
两个正数,绝对值大的正数大;
两个负数,
绝对值小的负数反而大,
绝对值大的负数反而小。
a、b两个数在数轴上的位置如图所示:
两个负数,绝对值大的反而小
0
a
b
负数比
较大小
转
化
正数比
较大小
比较下列每组数的大小:
(1)
(2)
比较下列每组数的大小:
(1)
(2)
0
a
b
试比较-a与-b的大小。
-b
-a
a、b两个数在数轴上的位置如图所示:
0
a
b
试比较-a与-b的大小。
a、b两个数在数轴上的位置如图所示:
因为
a>b
所以
-a<-b
2、正数大于0大于负数;
两个负数,绝对值大的反而小。
1、利用数轴;
有理数比较大小的方法:
绝对值与相反数
学校
小明家
小丽家
假如他们都步行上学,且速度相同,谁花的时间更少些呢?
3
km
2
km
小丽
学校
小明家
小丽家
3
km
2
km
A
B
数轴上表示一个数的点与原点的距离,叫做这个数的绝对值.
3
2
例1
求
4
和
-3.5
的绝对值
.
解:如图
A
B
4
3.5
因为点
A
与原点的距离是
4
,所以
4
的绝对值是
4
;记为
因为点
B
与原点的距离是
3.5
,所以-
3.5
的绝对值是
3.5
;记为
说一说:
你能说出数轴上点
A、B、C、D、E、F
各点所表示的数的绝对值吗?
点
A
表示
-5
,点
A
与原点的距离是
5
,所以
-5
的绝对值是
5
.记为|-5|
=
5.
B
F
E
D
C
A
点
B
表示
-3
,点
B
与原点的
距离是
3
,所以
-3
的绝对值是
3.
记为|-3|
=
3.
B
F
E
D
C
A
说一说:
你能说出数轴上点
A、B、C、D、E、F
各点所表示的数的绝对值吗?
点
C
表示
1
,点
C
与原点的距离是
1
,所以
1
的绝对值是
1.记为|1|
=
1.
B
F
E
D
C
A
说一说:
你能说出数轴上点
A、B、C、D、E、F
各点所表示的数的绝对值吗?
点
D
表示
2.5
,点
D
与原点的距离是
2.5
,所以
2.5
的绝对值是
2.5
.记为|2.5|
=
2.5.
B
F
E
D
C
A
说一说:
你能说出数轴上点
A、B、C、D、E、F
各点所表示的数的绝对值吗?
点
E
表示
5
,点
E
与原点的距
离是
5
,所以
5
的绝对值是
5.记为
|2.5|
=
2.5.
B
F
E
D
C
A
说一说:
你能说出数轴上点
A、B、C、D、E、F
各点所表示的数的绝对值吗?
点
F
表示
0
,点
F
与原点的距离是
0
,所以
0
的绝对值是
0
.记为|0|
=
0
.
B
F
E
D
C
A
说一说:
你能说出数轴上点
A、B、C、D、E、F
各点所表示的数的绝对值吗?
例2
比较
-3
和
-6
的绝对值的大小.
解:如图
A
B
3
6
先求出下列各式的值,再说出它们所表示的意义.
练一练
先求出下列各式的值,再说出它们所表示的意义.
练一练
你认为“任意有理数的绝对值都是正数”的说法正确吗?
任意一个有理数的绝对值是非负数.
比较下列各对数的大小:
练一练
动脑筋
有一天,甲、乙两个数在比谁
大.甲抢着说:“在数轴上我表示
的点到原点的距离比你表示的点到
原点的距离要大,看来我比你大”,
乙不甘示弱,紧接着说,“我是正
数,我大于零,也大于一切负数,
当然是我比你大”.你们说到底谁
大呢?
乙
甲
乙
甲
若甲是正数,由于甲表示的点到原点的距离比乙表示的点到原点的距离要大,所以甲比乙大;
若甲是负数,则显然乙比甲大.
B
D
C
A
C
、
D
两点到原点的距离相等,都等于3.
C
、
D
两点在原点的两侧,分别表示
-3
和
3
;
如图,观察数轴上
A、B
两点位置及其到原点的距离,你有什么发现?
5
5
3
3
A
、
B
两点在原点两侧,分别表示
-5
和
5
;
A
、
B
两点到原点的距离相等,都等于5.
D
C
A
B
E
F
G
H
例如:
E、F
两点分别表示
-2.5
和
2.5
;
5
5
与
3
3
2.5
2.5
-
与
与
与
观察下列
(+)
(+)
(+)
(+)
-
-
-
除
0
以外,任意一个有理数都由符号和绝对值两部分组成.
符号不同
绝对值相等
有理数,你有什么发现?
四对
-4.5
(
)
解:3的相反数是-3,
-4.5
的相反数是
4.5
,
例1
-
=
4.5
例2
解:
试一试:
化简―[―(+3.2)]
解:因为
+3.2
的相反数是
―3.2
,
所以
―(+3.2)=
―3.2
;
又因为
―3.2
的相反数是
3.2
,
所以
―[―(+3.2)]=
3.2
.
想一想:
请同学们仔细观察这五个等式,它们的符号变化有什么规律?
把一个数的多重符号化成单一符号时,若该数前面有奇数个“―”号,则化简的结果是负;
若该数前面有偶数个“―”号,则化简的结果是正.
-7
(1)-2的相反数是
,
3.75与
互为相反数,
相反数是其本身的数是
;
练一练:填空
(2)-(+7)=
,
-(-7)=
,
-[+(-7)]=
,
-[-(-7)]=
;
2
-3.75
0
-7
7
7
(3)判断下列语句,正确的是
.
①
―5
是相反数;
②
―5
与
+3
互为相反数;
③
―5
是
5
的相反数;
④
―5
和
5
互为相反数;
⑤
0
的相反数还是
0
.
③④⑤
(1)下列说法正确的是
(
)
A.正数的相反数是负数;
B.符号不同的两个数互为相反数;
C.π的相反数是
―3.14;
D.任何一个有理数都有相反数.
选择:
D
(2)一个数的相反数是非正数,那么这
个数一定是
(
)
A.正数
B.负数
C.零或正数
D.零
C
画一画:
在数轴上画出表示下列各数以及它们的相反数的点:
解:如图
A
B
C
D
A’
B’
(C’)
D’
如果改变有理数的符号,那么数轴上表示有理数的点的位置将会发生怎样的变化?
A
B
C
D
A’
B’
(C’)
D’
除
0
外,如果改变有理数的符号,那么数轴上表示有理数的点就从原点的一侧变到另一侧.
动脑筋:
如果数轴上两点
A、B
所表示的数互为相反数,点
A
在原点左侧,且
A、B
两点距离为
8
,你知道点
B
代表什么数吗?
答:点
B
代表
4
.
根据绝对值与相反数的意义填空:
(1)|2.3|=____,
|7/4|=_____,
|6|=_____
(2)|-5|=____,
|-10.5|=____,
|-7/4|=_____,
-5的相反数是___,-10.5的相反数是_____,
-7/4的相反数是_____,
(3)0的绝对值是____,0的相反数是_____
思考:一个数的绝对值与这个数本身、或与它的相反数之间有什么关系?你发现了什么?
2.3
7/4
10.5
5
5
6
7/4
0
10.5
7/4
0
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0
的绝对值是0.
归纳总结
符号表示
,
,
,
互为相反数的两个数的绝对值相等
互为相反数的两个数的绝对值有什么关系?
比较大小法则
两个正数,绝对值大的正数大;
两个负数,
绝对值小的负数反而大,
绝对值大的负数反而小。
a、b两个数在数轴上的位置如图所示:
两个负数,绝对值大的反而小
0
a
b
负数比
较大小
转
化
正数比
较大小
比较下列每组数的大小:
(1)
(2)
比较下列每组数的大小:
(1)
(2)
0
a
b
试比较-a与-b的大小。
-b
-a
a、b两个数在数轴上的位置如图所示:
0
a
b
试比较-a与-b的大小。
a、b两个数在数轴上的位置如图所示:
因为
a>b
所以
-a<-b
2、正数大于0大于负数;
两个负数,绝对值大的反而小。
1、利用数轴;
有理数比较大小的方法:
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
