苏科版七年级数学上册5.3 展开与折叠 教案
文档属性
| 名称 | 苏科版七年级数学上册5.3 展开与折叠 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1001.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 00:00:00 | ||
图片预览


文档简介
5.3 展开与折叠(1)
教学目标:
1.
通过展开、折叠,感受立体图形与平面图形的关系.
2.
能正确判断展开图是哪个几何体的展开图,并能画出简单的几何体的表面展开图.
3.经历和体验图形的变化过程,发展空间观念,养成研究性学习的良好习惯.
教学重点:认识长方体、正方体等简单几何体的侧面展开图。
教学难点:认识长方体、正方体的侧面展开图,增强空间观念。
引入
生命
“展”翅高飞:
展开,只为更高、更远……
展开,才能探索更多未知……
生活
“展”露智慧:
展开,只为更小、更省……
展开,才能更好地适应环境…
生长
小明想做一个如图所示的圆柱形纸筒(有两个底面).需要准备怎样的平面图形?请你画一画;(教师手里拿一个纸板模型)
预设:学生回答“一个长方形和两个圆”(生画在黑板上)
教师:你怎么验证你的结论?
生:我将圆柱体剪开来(展开),学生操作,讲解怎样剪开;
师:请观察剪开的图形,它有几个部分组成?分别和圆柱的那个面(部分)对应?
生:三个部分,一个长方形和两个圆;其中的长方形和圆柱的侧面对应、两个圆与圆柱的两个底面对应;
师:根据刚才的图形对应,你能找到展开前后一些数量不变的量吗?
生:圆柱的底面圆的周长与长方形的长相等、圆柱的高与长方形的宽相等;
师:很好,我们要学会用数学的眼光从数、形不同的视角观察、研究立体图形的展开,这就是我们今天要研究的话题——展开与折叠(1)
(教师板书课题)
新授
1、问题:除了圆柱,我们还知道有很多的几何体存在,那么它们是否也都能展开成平面图形呢?
先看看几个简单的立体图形(板书:立体图形,给圆柱编号1)
2、将圆锥形冰激凌纸筒的侧面沿虚线剪开,得到什么平面图形?
追问:如果是有盖子的呢?
(1)怎样剪能得到平面图形?
(2)得到什么样的平面图形?
或设计:
如图是有盖子圆锥形纸筒,将其表面展开.
(1)怎样剪能得到平面图形?
(2)得到什么样的平面图形?(注意观察数、形的关联)
总结:圆锥的表面展开图
沿着圆锥的顶点与底面圆周上任一点的连线以及底面圆周把圆锥剪开,就得到圆锥的表面展开图.圆锥的表面展开图是一个圆和一个扇形,如图所示.
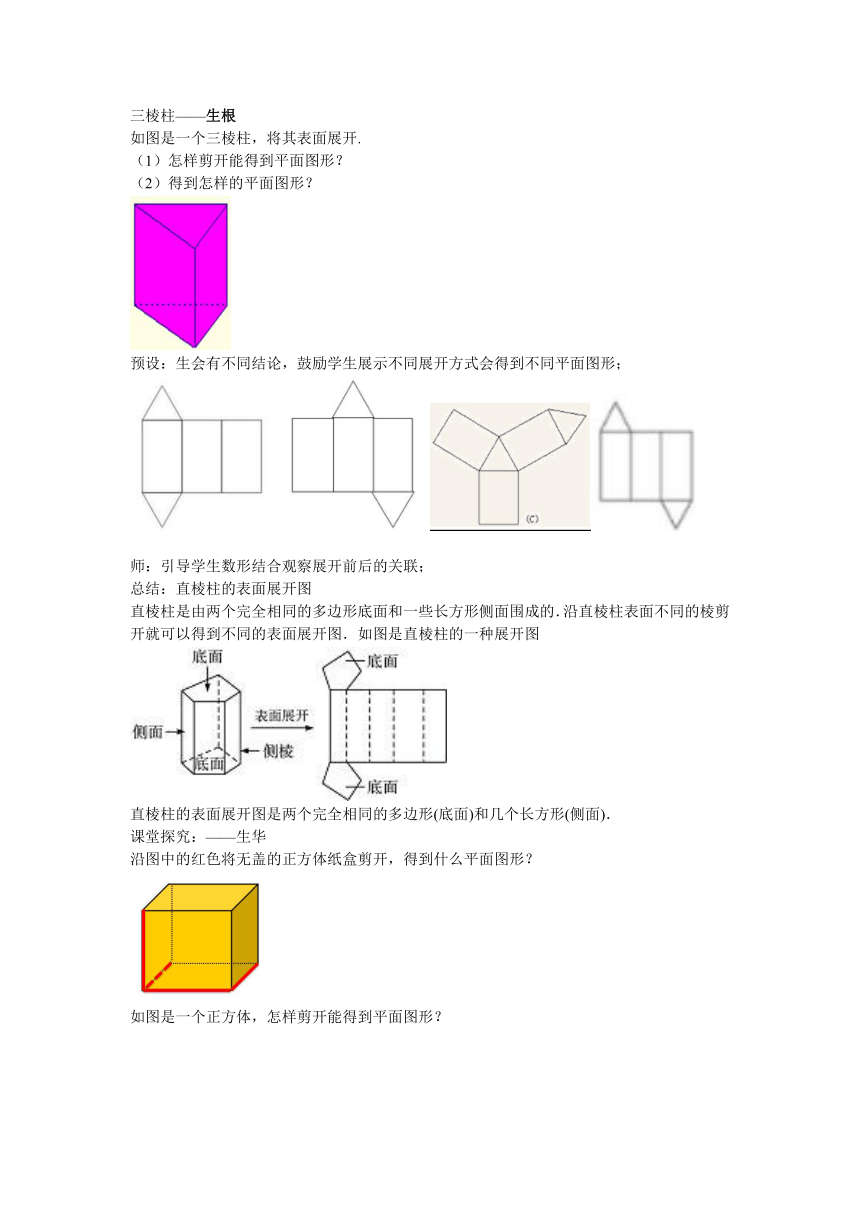
三棱柱——生根
如图是一个三棱柱,将其表面展开.
(1)怎样剪开能得到平面图形?
(2)得到怎样的平面图形?
预设:生会有不同结论,鼓励学生展示不同展开方式会得到不同平面图形;
师:引导学生数形结合观察展开前后的关联;
总结:直棱柱的表面展开图
直棱柱是由两个完全相同的多边形底面和一些长方形侧面围成的.沿直棱柱表面不同的棱剪开就可以得到不同的表面展开图.如图是直棱柱的一种展开图
直棱柱的表面展开图是两个完全相同的多边形(底面)和几个长方形(侧面).
课堂探究:——生华
沿图中的红色将无盖的正方体纸盒剪开,得到什么平面图形?
如图是一个正方体,怎样剪开能得到平面图形?
把一个正方体沿部分棱剪开展成一个平面图形.
把你得到的平面图形与同学交流:
(1)在你的操作过程中,剪开了几条棱?
(2)你们组汇总出了几种不同的表面展开图?
课后实践时间
请你将一个长方体纸盒沿部分棱剪开展开成平面图形,把你得到的平面图形与同学交流.
棱锥——生态
如图,将三棱锥的表面展开.
1、怎样剪能得到平面图形?
2、得到什么样的平面图形?
变式:换一个四个面都是等边三角形的棱锥试试.
追问:
如图,将一个四棱锥的表面展开.
1、怎样剪能得到平面图形?
2、得到什么样的平面图形?
预设:改为学生猜想,直接画图展示,有必要的后续再操作验证;
牛
刀
小
试
如图,哪一个是棱锥侧面展开图?
辩一辩
如图,上面的图形分别是下面哪个立体图形展开的形状?把它们用线连起来。
生疑——请你思考:球体能否剪开成为平面图形?以手中的乒乓球为例试试看.
生慧
如图:一只无盖圆桶的下方有一只壁虎,上方有一只蚊子,壁虎要想尽快吃到蚊子,应该走哪条路径?
小结
飞翔时,鸟儿展开翅膀,让自己飞得更远...
学习时,我们展开想象,让思维更加深入...
从立体到平面,让数学更有生命力...
课后练习:见课后练习案
教学目标:
1.
通过展开、折叠,感受立体图形与平面图形的关系.
2.
能正确判断展开图是哪个几何体的展开图,并能画出简单的几何体的表面展开图.
3.经历和体验图形的变化过程,发展空间观念,养成研究性学习的良好习惯.
教学重点:认识长方体、正方体等简单几何体的侧面展开图。
教学难点:认识长方体、正方体的侧面展开图,增强空间观念。
引入
生命
“展”翅高飞:
展开,只为更高、更远……
展开,才能探索更多未知……
生活
“展”露智慧:
展开,只为更小、更省……
展开,才能更好地适应环境…
生长
小明想做一个如图所示的圆柱形纸筒(有两个底面).需要准备怎样的平面图形?请你画一画;(教师手里拿一个纸板模型)
预设:学生回答“一个长方形和两个圆”(生画在黑板上)
教师:你怎么验证你的结论?
生:我将圆柱体剪开来(展开),学生操作,讲解怎样剪开;
师:请观察剪开的图形,它有几个部分组成?分别和圆柱的那个面(部分)对应?
生:三个部分,一个长方形和两个圆;其中的长方形和圆柱的侧面对应、两个圆与圆柱的两个底面对应;
师:根据刚才的图形对应,你能找到展开前后一些数量不变的量吗?
生:圆柱的底面圆的周长与长方形的长相等、圆柱的高与长方形的宽相等;
师:很好,我们要学会用数学的眼光从数、形不同的视角观察、研究立体图形的展开,这就是我们今天要研究的话题——展开与折叠(1)
(教师板书课题)
新授
1、问题:除了圆柱,我们还知道有很多的几何体存在,那么它们是否也都能展开成平面图形呢?
先看看几个简单的立体图形(板书:立体图形,给圆柱编号1)
2、将圆锥形冰激凌纸筒的侧面沿虚线剪开,得到什么平面图形?
追问:如果是有盖子的呢?
(1)怎样剪能得到平面图形?
(2)得到什么样的平面图形?
或设计:
如图是有盖子圆锥形纸筒,将其表面展开.
(1)怎样剪能得到平面图形?
(2)得到什么样的平面图形?(注意观察数、形的关联)
总结:圆锥的表面展开图
沿着圆锥的顶点与底面圆周上任一点的连线以及底面圆周把圆锥剪开,就得到圆锥的表面展开图.圆锥的表面展开图是一个圆和一个扇形,如图所示.
三棱柱——生根
如图是一个三棱柱,将其表面展开.
(1)怎样剪开能得到平面图形?
(2)得到怎样的平面图形?
预设:生会有不同结论,鼓励学生展示不同展开方式会得到不同平面图形;
师:引导学生数形结合观察展开前后的关联;
总结:直棱柱的表面展开图
直棱柱是由两个完全相同的多边形底面和一些长方形侧面围成的.沿直棱柱表面不同的棱剪开就可以得到不同的表面展开图.如图是直棱柱的一种展开图
直棱柱的表面展开图是两个完全相同的多边形(底面)和几个长方形(侧面).
课堂探究:——生华
沿图中的红色将无盖的正方体纸盒剪开,得到什么平面图形?
如图是一个正方体,怎样剪开能得到平面图形?
把一个正方体沿部分棱剪开展成一个平面图形.
把你得到的平面图形与同学交流:
(1)在你的操作过程中,剪开了几条棱?
(2)你们组汇总出了几种不同的表面展开图?
课后实践时间
请你将一个长方体纸盒沿部分棱剪开展开成平面图形,把你得到的平面图形与同学交流.
棱锥——生态
如图,将三棱锥的表面展开.
1、怎样剪能得到平面图形?
2、得到什么样的平面图形?
变式:换一个四个面都是等边三角形的棱锥试试.
追问:
如图,将一个四棱锥的表面展开.
1、怎样剪能得到平面图形?
2、得到什么样的平面图形?
预设:改为学生猜想,直接画图展示,有必要的后续再操作验证;
牛
刀
小
试
如图,哪一个是棱锥侧面展开图?
辩一辩
如图,上面的图形分别是下面哪个立体图形展开的形状?把它们用线连起来。
生疑——请你思考:球体能否剪开成为平面图形?以手中的乒乓球为例试试看.
生慧
如图:一只无盖圆桶的下方有一只壁虎,上方有一只蚊子,壁虎要想尽快吃到蚊子,应该走哪条路径?
小结
飞翔时,鸟儿展开翅膀,让自己飞得更远...
学习时,我们展开想象,让思维更加深入...
从立体到平面,让数学更有生命力...
课后练习:见课后练习案
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
