苏科版七年级数学上册3.2代数式课件(26张ppt)
文档属性
| 名称 | 苏科版七年级数学上册3.2代数式课件(26张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
代数式
练习:
1.某城市市区人口a万人,市区绿地面积m万,则平均每个人拥有绿地___
2.某城市5年前人均年收入为n元,预计今年人均收入是5年前的2倍多500元,那么今年人均收入将达___
_
元.
3.如图,这个长方体的体积是____,表面积是_____.
(2n+50)
abc
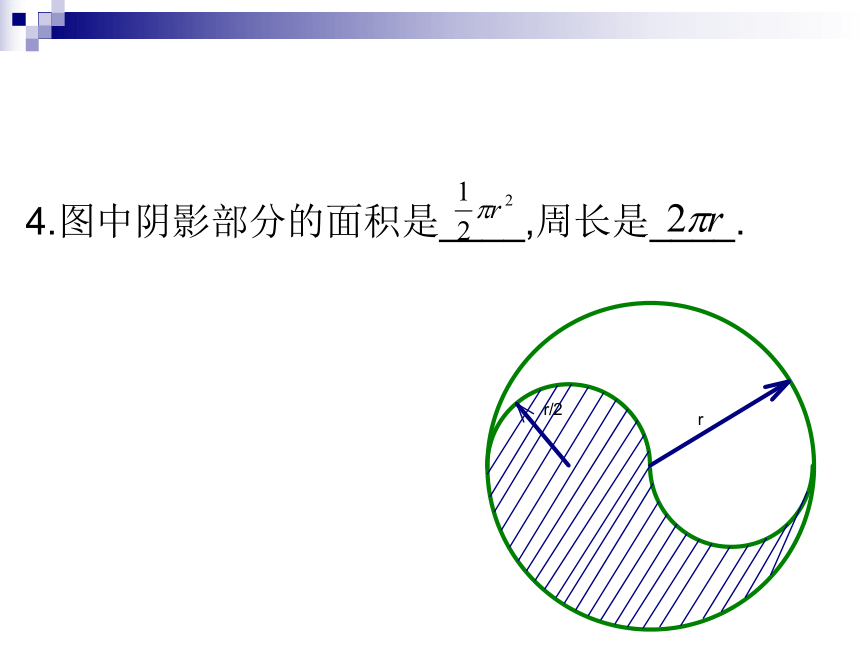
4.图中阴影部分的面积是____,周长是____.
单独一个数或一个字母也是代数式.
像
、2n+500、abc、
2(ab+bc+ac)
、
、
等式子都是
.
代数式
代数式是用基本运算符号把数或表示数的字母连接起来的式子。
1、代数式中除了含有数,字母和运算符号外,还可以含有括号。
2、
单独一个数或一个字母也是代数式。
3、式子不含“=”、“>”、“<”、“≤”、“≥”
(运算符号包括加、减、乘、除、乘方)
注意:
(3)数字与字母相乘,数字通常写在字母前面;
(1)
a×b
通常写作
a·b
或
ab
;
如:a×3通常写作3a
(4)带分数一般写成假分数.
如:
×a
通常写作
a
代数式的规范写法:
(5)数字与数字相乘,一般仍用“×”号,即“×”号不能省略
如1÷a
通常写作
;
(2)除法运算写成分数形式。
①0.9a
②x+5=9
③x>y
④a+b<4
⑤15×1.5℅m
⑥
⑦
⑧
⑨
a+b
是代数式的有:①⑤⑥⑦⑧⑨
练一练.
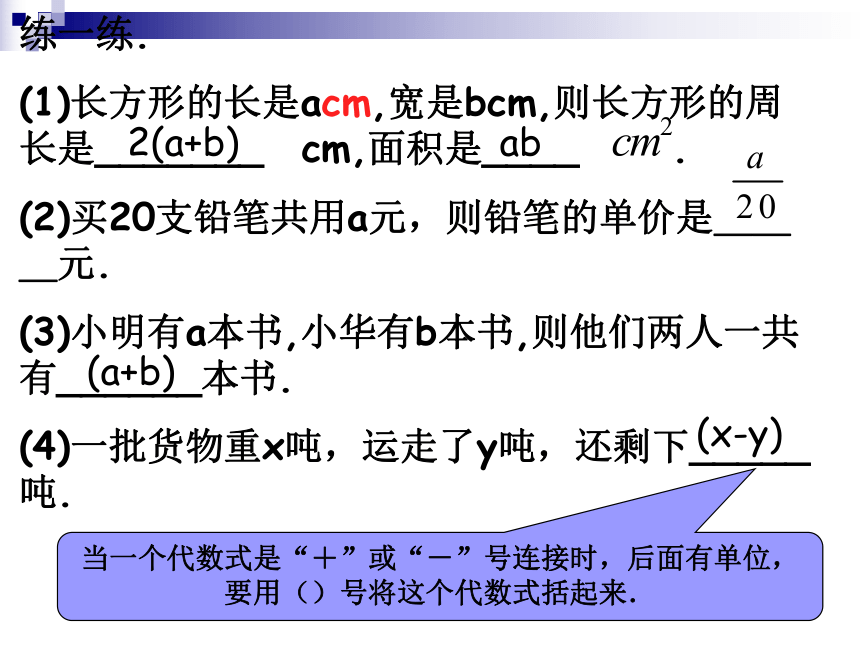
(1)长方形的长是acm,宽是bcm,则长方形的周长是_______ cm,面积是____
.
(2)买20支铅笔共用a元,则铅笔的单价是___元.
(3)小明有a本书,小华有b本书,则他们两人一共有______本书.
(4)一批货物重x吨,运走了y吨,还剩下_____吨.
2(a+b)
ab
(a+b)
(x-y)
当一个代数式是“+”或“-”号连接时,后面有单位,要用()号将这个代数式括起来.
做一做:
请同学们思考以下问题并填空:
某地区夏季高山上的温度从山脚处开始每升高100米降低0.7?C.如果山脚温度是28?C,那么山上300米处的温度为________.一般地,山上x米处的温度
为_____________.
25.9?C
?C
通过以上问题的解决,说明了为什么要学习列代数式。在解决一些实际问题时,往往先把问题中与数量有关的词语用代数式表示出来,即列出代数式,使问题变得更简洁,更具一般性。
例1:设某数为x,用代数式表示:
(1)
比某数的
大1的数;
(2)
比某数大10%的数;
(3)
某数与
的和的3倍;
(4)
某数的倒数与5的差.
解:
(1)
(2)(1+10%)x
(3)
(4)
例2.用代数式表示
(1)
a、b两数的平方和减去他们乘积的2倍;
(2)
a、b两数的和的平方减去他们的差的平方;
(3)
a、b两数的和与他们的差的乘积;
(4)
偶数、奇数.
解:
(1)
a?
+b?–2ab
(2)(
a+b)?
–(a–b)?
(3)(a+b)(a–b)
(4)2n,2n+1(n为整数)
一.课中巩固
1.小明买铅笔5支,买练习本4本,其中铅笔X元一支,练习本Y元一本,那么他应付给商店多少元?
应付给商店(5x+4y)元
2.某校梯形教室第一排有8个座位,第二排有10个座位,以后每排均比它前一排多2个座位
,那么第n排有多少个座位?
第n排有[8+2(n-1)]个
请用代数式表示下列问题
例3:3月12日嘉积中学校团委组织260
名学生
(其中女生b人)去市万泉河旁植树,每个男生植树x棵,每个女生植树y棵,你能用代数式表示共植树的棵数吗?
分析:因为女生为b人,所以男生有
人
(260-b)
男生共植树
棵
(260-b)x
女生植树
棵
by
共植树
棵
(260-b)x+by
例4,
(1)一个两位数的个位数a是,十位数是b,这个两位数是_______;
(2)一个三位数个位数为a,前两位为b,则该两位数可表示为_______;
(3)一个五位数,前三位为a,后两位为b,则该五位数可表示为_______;
10b+a
10b+a
100a+b
1.
用代数式表示:
(1)a与b的差的2倍;
(2)a与b的2倍的差;
(3)a与b、c两数之和的差(4)a、b两数之差与c的和.
2.
填空:
(1)连续三个整数,中间一个是n,则第一个和第三个整数分别是_______、______;
(2)连续三个偶数,中间一个是2n,则第一个和第三个偶数分别是__________、__________.
3.
琼海市出租车收费标准为:起步价3元,2千米后每千米价1.4元.则某人乘坐出租车x(x>2)千米的付费为___________元.
练习
n-1
n+1
2n-2
2n+2
[3+1.4(X-2)
]
(1)2(a-b);(2)a-2b;(3)a-(b+c);(4)a-b+c.
要正确写出代数式要注意
(1)审清题,弄懂一些术语
(2)抓住关键词,弄清运算顺序
(3)一般先读的先写
同时一个代数式可表示不同的意义。
在代数式中同一意义的量应用同一个字母表示,不同意义的量应用不同的字母表示。
(4)用代数式表示应用问题时,还弄清题中的数量关系。
单项式
注:单独一个数或一个字母也是单项式
单项式中的数字因数叫做这个单项式的系数
单项式中所有字母的指数的和叫做这个单项式的次数.
如果一个单项式只含有字母因数,它的系数就是1或者-1,
例如ab就是1·ab,系数是1
再如-n就是-1·n,系数是-1
单项式
8x
系数
次数
注:单项式的系数要
连同其前面的符号
8
-2
1
-1
1
4
3
2
2
2
1
定义:几个单项式的和叫做多项式
其中每个单项式叫做多项式的项
例:a+b这个多项式由两项组成,它的项是a,b
2x-3y这个多项式的项是2x,-3y
注:在说多项式的项的时候要连同前面的符号
次数最高项的次数,叫做这个多项式的次数.
单项式和多项式统称整式
下列代数式中哪些是单项式?
哪些是
多项式?如果是单项式,它的系数又是多少?
a+b+c
-3
-6+x
-xy
-1
a
多项式
多项式
多项式
单项式,系数-3
单项式,系数
单项式,系数1
单项式
单项式,系数-1
例题:
(1).小军100m赛跑时用了
t
s,那么小军跑完
100m的平均速度是多少?
解:小军跑完100m的平均速度是
m/s.
(2).长方形的周长为16㎝,一边长为a
㎝,这个
长方形的面积是多少?
解:这个长方形的面积是a(8-a)
列代数式时:
数字与字母、字母与字母相乘,乘号
通常用“
”表示或省略不写,并且把数
字写在字母的前面.
除法运算通常写成分数的形式.
1.下面各小题的代数式,书写是否符合规范,
符合的在(
)里打√,错的打×.
(1)
a·3
(
)
(2)
x+5(
)
(4)(t-4)
℃
(
)
(6)2·3·x·y
(
)
×
√
√
√
×
×
(
)
(
)
友情提醒
1.用字母表示数时,数与字母,字母与字母中的乘号可以省略不写;或用“·”表示.
例a×b记为ab.
2.字母和数字相乘时,省略乘号,并把数字放到字母前.例a×4记为4a.
3.出现除式时,用分数表示.例a÷2记为a/2.
4.结果含加减运算的,单位前加“(
)”.例“a+2岁”应为(a+2)岁.
5.系数是带分数时,带分数要化成假分数.
这节课的收获是……
我想说
代数式
练习:
1.某城市市区人口a万人,市区绿地面积m万,则平均每个人拥有绿地___
2.某城市5年前人均年收入为n元,预计今年人均收入是5年前的2倍多500元,那么今年人均收入将达___
_
元.
3.如图,这个长方体的体积是____,表面积是_____.
(2n+50)
abc
4.图中阴影部分的面积是____,周长是____.
单独一个数或一个字母也是代数式.
像
、2n+500、abc、
2(ab+bc+ac)
、
、
等式子都是
.
代数式
代数式是用基本运算符号把数或表示数的字母连接起来的式子。
1、代数式中除了含有数,字母和运算符号外,还可以含有括号。
2、
单独一个数或一个字母也是代数式。
3、式子不含“=”、“>”、“<”、“≤”、“≥”
(运算符号包括加、减、乘、除、乘方)
注意:
(3)数字与字母相乘,数字通常写在字母前面;
(1)
a×b
通常写作
a·b
或
ab
;
如:a×3通常写作3a
(4)带分数一般写成假分数.
如:
×a
通常写作
a
代数式的规范写法:
(5)数字与数字相乘,一般仍用“×”号,即“×”号不能省略
如1÷a
通常写作
;
(2)除法运算写成分数形式。
①0.9a
②x+5=9
③x>y
④a+b<4
⑤15×1.5℅m
⑥
⑦
⑧
⑨
a+b
是代数式的有:①⑤⑥⑦⑧⑨
练一练.
(1)长方形的长是acm,宽是bcm,则长方形的周长是_______ cm,面积是____
.
(2)买20支铅笔共用a元,则铅笔的单价是___元.
(3)小明有a本书,小华有b本书,则他们两人一共有______本书.
(4)一批货物重x吨,运走了y吨,还剩下_____吨.
2(a+b)
ab
(a+b)
(x-y)
当一个代数式是“+”或“-”号连接时,后面有单位,要用()号将这个代数式括起来.
做一做:
请同学们思考以下问题并填空:
某地区夏季高山上的温度从山脚处开始每升高100米降低0.7?C.如果山脚温度是28?C,那么山上300米处的温度为________.一般地,山上x米处的温度
为_____________.
25.9?C
?C
通过以上问题的解决,说明了为什么要学习列代数式。在解决一些实际问题时,往往先把问题中与数量有关的词语用代数式表示出来,即列出代数式,使问题变得更简洁,更具一般性。
例1:设某数为x,用代数式表示:
(1)
比某数的
大1的数;
(2)
比某数大10%的数;
(3)
某数与
的和的3倍;
(4)
某数的倒数与5的差.
解:
(1)
(2)(1+10%)x
(3)
(4)
例2.用代数式表示
(1)
a、b两数的平方和减去他们乘积的2倍;
(2)
a、b两数的和的平方减去他们的差的平方;
(3)
a、b两数的和与他们的差的乘积;
(4)
偶数、奇数.
解:
(1)
a?
+b?–2ab
(2)(
a+b)?
–(a–b)?
(3)(a+b)(a–b)
(4)2n,2n+1(n为整数)
一.课中巩固
1.小明买铅笔5支,买练习本4本,其中铅笔X元一支,练习本Y元一本,那么他应付给商店多少元?
应付给商店(5x+4y)元
2.某校梯形教室第一排有8个座位,第二排有10个座位,以后每排均比它前一排多2个座位
,那么第n排有多少个座位?
第n排有[8+2(n-1)]个
请用代数式表示下列问题
例3:3月12日嘉积中学校团委组织260
名学生
(其中女生b人)去市万泉河旁植树,每个男生植树x棵,每个女生植树y棵,你能用代数式表示共植树的棵数吗?
分析:因为女生为b人,所以男生有
人
(260-b)
男生共植树
棵
(260-b)x
女生植树
棵
by
共植树
棵
(260-b)x+by
例4,
(1)一个两位数的个位数a是,十位数是b,这个两位数是_______;
(2)一个三位数个位数为a,前两位为b,则该两位数可表示为_______;
(3)一个五位数,前三位为a,后两位为b,则该五位数可表示为_______;
10b+a
10b+a
100a+b
1.
用代数式表示:
(1)a与b的差的2倍;
(2)a与b的2倍的差;
(3)a与b、c两数之和的差(4)a、b两数之差与c的和.
2.
填空:
(1)连续三个整数,中间一个是n,则第一个和第三个整数分别是_______、______;
(2)连续三个偶数,中间一个是2n,则第一个和第三个偶数分别是__________、__________.
3.
琼海市出租车收费标准为:起步价3元,2千米后每千米价1.4元.则某人乘坐出租车x(x>2)千米的付费为___________元.
练习
n-1
n+1
2n-2
2n+2
[3+1.4(X-2)
]
(1)2(a-b);(2)a-2b;(3)a-(b+c);(4)a-b+c.
要正确写出代数式要注意
(1)审清题,弄懂一些术语
(2)抓住关键词,弄清运算顺序
(3)一般先读的先写
同时一个代数式可表示不同的意义。
在代数式中同一意义的量应用同一个字母表示,不同意义的量应用不同的字母表示。
(4)用代数式表示应用问题时,还弄清题中的数量关系。
单项式
注:单独一个数或一个字母也是单项式
单项式中的数字因数叫做这个单项式的系数
单项式中所有字母的指数的和叫做这个单项式的次数.
如果一个单项式只含有字母因数,它的系数就是1或者-1,
例如ab就是1·ab,系数是1
再如-n就是-1·n,系数是-1
单项式
8x
系数
次数
注:单项式的系数要
连同其前面的符号
8
-2
1
-1
1
4
3
2
2
2
1
定义:几个单项式的和叫做多项式
其中每个单项式叫做多项式的项
例:a+b这个多项式由两项组成,它的项是a,b
2x-3y这个多项式的项是2x,-3y
注:在说多项式的项的时候要连同前面的符号
次数最高项的次数,叫做这个多项式的次数.
单项式和多项式统称整式
下列代数式中哪些是单项式?
哪些是
多项式?如果是单项式,它的系数又是多少?
a+b+c
-3
-6+x
-xy
-1
a
多项式
多项式
多项式
单项式,系数-3
单项式,系数
单项式,系数1
单项式
单项式,系数-1
例题:
(1).小军100m赛跑时用了
t
s,那么小军跑完
100m的平均速度是多少?
解:小军跑完100m的平均速度是
m/s.
(2).长方形的周长为16㎝,一边长为a
㎝,这个
长方形的面积是多少?
解:这个长方形的面积是a(8-a)
列代数式时:
数字与字母、字母与字母相乘,乘号
通常用“
”表示或省略不写,并且把数
字写在字母的前面.
除法运算通常写成分数的形式.
1.下面各小题的代数式,书写是否符合规范,
符合的在(
)里打√,错的打×.
(1)
a·3
(
)
(2)
x+5(
)
(4)(t-4)
℃
(
)
(6)2·3·x·y
(
)
×
√
√
√
×
×
(
)
(
)
友情提醒
1.用字母表示数时,数与字母,字母与字母中的乘号可以省略不写;或用“·”表示.
例a×b记为ab.
2.字母和数字相乘时,省略乘号,并把数字放到字母前.例a×4记为4a.
3.出现除式时,用分数表示.例a÷2记为a/2.
4.结果含加减运算的,单位前加“(
)”.例“a+2岁”应为(a+2)岁.
5.系数是带分数时,带分数要化成假分数.
这节课的收获是……
我想说
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
