平面图形的周长和面积 复习教案
图片预览

文档简介
平面图形的周长和面积
教学目标
【知识教学点】
熟练掌握平面图形面积计算公式和周长计算公式及其应用。
【能力教学点】
渗透数学思想中的转化思想,提高学生的学习能力。
【德育教学点】
培养学生认真审题的良好学习习惯。
教学过程
第一环节:复习平面图形的基本概念。
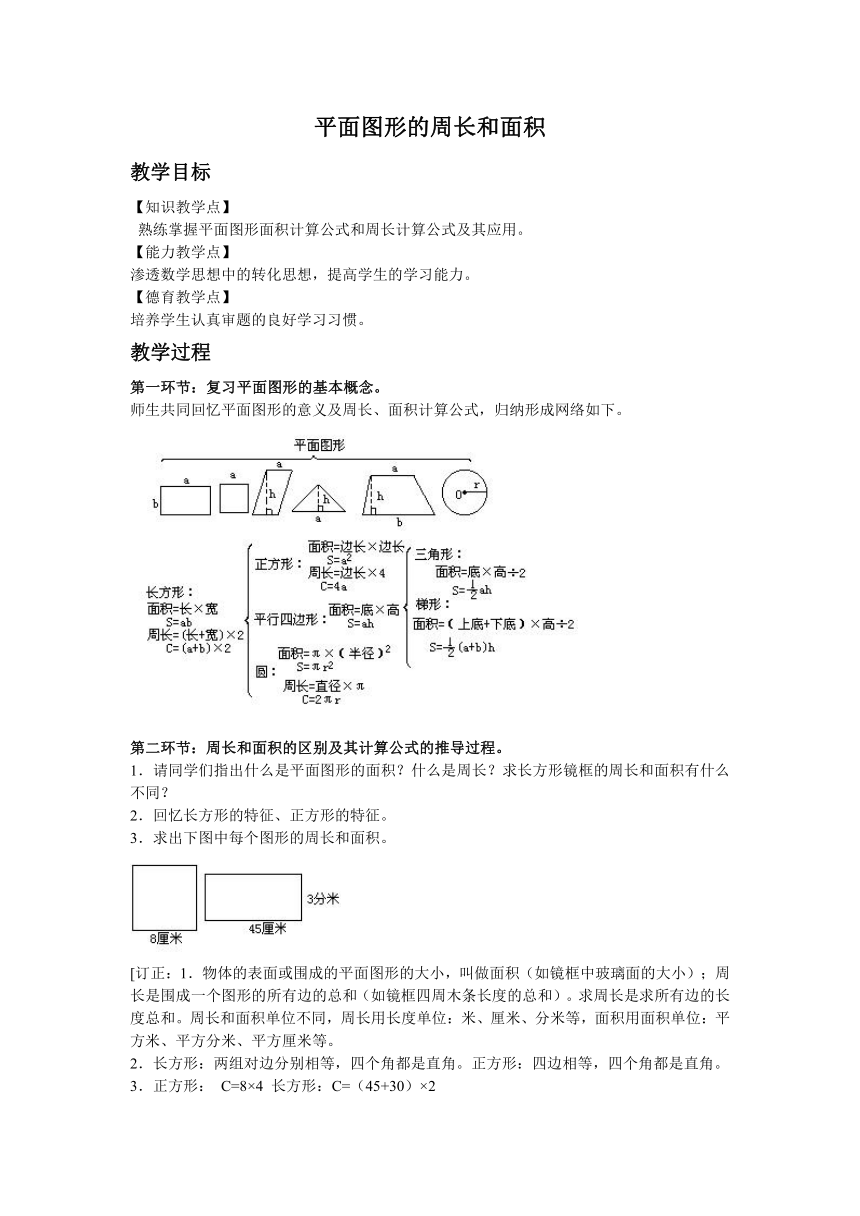
师生共同回忆平面图形的意义及周长、面积计算公式,归纳形成网络如下。
第二环节:周长和面积的区别及其计算公式的推导过程。
1.请同学们指出什么是平面图形的面积?什么是周长?求长方形镜框的周长和面积有什么不同?
2.回忆长方形的特征、正方形的特征。
3.求出下图中每个图形的周长和面积。
[订正:1.物体的表面或围成的平面图形的大小,叫做面积(如镜框中玻璃面的大小);周长是围成一个图形的所有边的总和(如镜框四周木条长度的总和)。求周长是求所有边的长度总和。周长和面积单位不同,周长用长度单位:米、厘米、分米等,面积用面积单位:平方米、平方分米、平方厘米等。
2.长方形:两组对边分别相等,四个角都是直角。正方形:四边相等,四个角都是直角。
3.正方形: C=8×4 长方形:C=(45+30)×2
=32(厘米) =150(厘米)
S=8×8 S=45×30
=64(平方厘米) =1350(平方厘米)]
4.回忆思考什么叫平行四边形?它的面积计算公式是怎样推导的?三角形面积计算公式是怎样推导的?
[订正:两组对边分别平行的四边形叫平行四边形。利用转化思想,采取割补平移,将平行四边形拼成长方形。
因为长方形面积=长×宽
所以平行四边形面积=底×高
由两个完全一样的三角形可以拼成一个平行四边形,三角形的底相当于平行四边形的底,三角形的高相当于平行四边形的高。
所以三角形面积=底×高÷2]
5.根据以上的公式,求出下面各图形的面积。(单位:厘米)
[订正:(1)12×5÷2=30(平方厘米)
(2)11×8÷2=44(平方厘米)
(3)26×9÷2=117(平方厘米)]
6.思考后回答,梯形的特征是什么?你能根据三角形面积公式的推导方法说出梯形面积公式是怎样推导的吗?求出下面各梯形的面积。(单位厘米)
[订正:只有一组对边平行的四边形叫梯形。用两个完全一样的梯形可以拼成一个平行四边形。
所以,梯形面积=(上底+下底)×高÷2
(1)150平方厘米(2)480平方厘米(3)390平方厘米]
7.想一想,圆与前面的几种图形的最大区别是什么?圆的周长和面积的计算公式是怎样推导的?求下面圆的面积。(单位:厘米)
[订正:圆是曲线围成的图形。圆的周长总是直径的3倍多一点,即圆周长和直径的比是一个固定不变的值,也就是π。
周长=直径×π C=πd
把圆分成若干个相等的扇形拼成近似的长方形,长方形的长是圆周长的一半,宽是半径。
圆面积=半径2×π S=πr2
(1)3.14×62=113.04(平方厘米)
(2)3.14×(12.56÷3.14÷2)2=12.56(平方厘米)]
第三环节:巩固练习
1.判断。
(1)边长4厘米的正方形的周长和面积是相等的。( )
(2)半圆的周长是圆周长的一半。( )
(3)两个面积相等的三角形一定可以拼成一个平行四边形。
( )
(4)两个完全一样的等腰直角三角形一定可以拼成正方形。
( )
(5)圆和正方形的周长相等时,圆的面积比正方形的面积大。
( )
(6)三角形的面积是平行四边形面积的一半。 ( )
(7)大圆的半径是小圆半径的2倍,则小圆的面积是大圆面积的一半。
( )
2.求出下面各图形的周长。(单位:分米)
3.求出下面各图形的面积。(单位:厘米,保留一位小数。)
4.一个长方形和一个圆的周长相等,已知长方形的长是8.4厘米,宽是4.16厘米,圆的面积是多少?
[订正:
1.(1)×(2)×(3)×(4)√(5)√(6)×(7)×
2.(1)13×4=52(分米)
(2)(40+15)×2=110(分米)
(3)3.14×(6×2)÷2+6×2=30.84(分米)
3.(1)(2+4)×1.8÷2=5.4(平方厘米)
(2)3.14×(4.5÷2)2÷2≈7.9(平方厘米)
(3)5.5×1÷2≈2.8(平方厘米)
(4)4.5×1.5≈6.8(平方厘米)]
第四环节:综合提高性练习。(供学有余力的学生解答)
1.求下图阴影部分面积。(单位:厘米)
[提示:(1)把②移到靠近①处,便组成一个正方形,而阴影部分则是一个小长方形。解:3×(5-3)=6(平方厘米)
(2)解:求大小正方形面积和:52+32=34(平方厘米)
求大正方形面积的一半:52÷2=12.5(平方厘米)
求三角形面积:(5+3)×3÷2=12(平方厘米)
求阴影面积:34-12.5-12=9.5(平方厘米)]
第五环节:布置作业。(略)
教学目标
【知识教学点】
熟练掌握平面图形面积计算公式和周长计算公式及其应用。
【能力教学点】
渗透数学思想中的转化思想,提高学生的学习能力。
【德育教学点】
培养学生认真审题的良好学习习惯。
教学过程
第一环节:复习平面图形的基本概念。
师生共同回忆平面图形的意义及周长、面积计算公式,归纳形成网络如下。
第二环节:周长和面积的区别及其计算公式的推导过程。
1.请同学们指出什么是平面图形的面积?什么是周长?求长方形镜框的周长和面积有什么不同?
2.回忆长方形的特征、正方形的特征。
3.求出下图中每个图形的周长和面积。
[订正:1.物体的表面或围成的平面图形的大小,叫做面积(如镜框中玻璃面的大小);周长是围成一个图形的所有边的总和(如镜框四周木条长度的总和)。求周长是求所有边的长度总和。周长和面积单位不同,周长用长度单位:米、厘米、分米等,面积用面积单位:平方米、平方分米、平方厘米等。
2.长方形:两组对边分别相等,四个角都是直角。正方形:四边相等,四个角都是直角。
3.正方形: C=8×4 长方形:C=(45+30)×2
=32(厘米) =150(厘米)
S=8×8 S=45×30
=64(平方厘米) =1350(平方厘米)]
4.回忆思考什么叫平行四边形?它的面积计算公式是怎样推导的?三角形面积计算公式是怎样推导的?
[订正:两组对边分别平行的四边形叫平行四边形。利用转化思想,采取割补平移,将平行四边形拼成长方形。
因为长方形面积=长×宽
所以平行四边形面积=底×高
由两个完全一样的三角形可以拼成一个平行四边形,三角形的底相当于平行四边形的底,三角形的高相当于平行四边形的高。
所以三角形面积=底×高÷2]
5.根据以上的公式,求出下面各图形的面积。(单位:厘米)
[订正:(1)12×5÷2=30(平方厘米)
(2)11×8÷2=44(平方厘米)
(3)26×9÷2=117(平方厘米)]
6.思考后回答,梯形的特征是什么?你能根据三角形面积公式的推导方法说出梯形面积公式是怎样推导的吗?求出下面各梯形的面积。(单位厘米)
[订正:只有一组对边平行的四边形叫梯形。用两个完全一样的梯形可以拼成一个平行四边形。
所以,梯形面积=(上底+下底)×高÷2
(1)150平方厘米(2)480平方厘米(3)390平方厘米]
7.想一想,圆与前面的几种图形的最大区别是什么?圆的周长和面积的计算公式是怎样推导的?求下面圆的面积。(单位:厘米)
[订正:圆是曲线围成的图形。圆的周长总是直径的3倍多一点,即圆周长和直径的比是一个固定不变的值,也就是π。
周长=直径×π C=πd
把圆分成若干个相等的扇形拼成近似的长方形,长方形的长是圆周长的一半,宽是半径。
圆面积=半径2×π S=πr2
(1)3.14×62=113.04(平方厘米)
(2)3.14×(12.56÷3.14÷2)2=12.56(平方厘米)]
第三环节:巩固练习
1.判断。
(1)边长4厘米的正方形的周长和面积是相等的。( )
(2)半圆的周长是圆周长的一半。( )
(3)两个面积相等的三角形一定可以拼成一个平行四边形。
( )
(4)两个完全一样的等腰直角三角形一定可以拼成正方形。
( )
(5)圆和正方形的周长相等时,圆的面积比正方形的面积大。
( )
(6)三角形的面积是平行四边形面积的一半。 ( )
(7)大圆的半径是小圆半径的2倍,则小圆的面积是大圆面积的一半。
( )
2.求出下面各图形的周长。(单位:分米)
3.求出下面各图形的面积。(单位:厘米,保留一位小数。)
4.一个长方形和一个圆的周长相等,已知长方形的长是8.4厘米,宽是4.16厘米,圆的面积是多少?
[订正:
1.(1)×(2)×(3)×(4)√(5)√(6)×(7)×
2.(1)13×4=52(分米)
(2)(40+15)×2=110(分米)
(3)3.14×(6×2)÷2+6×2=30.84(分米)
3.(1)(2+4)×1.8÷2=5.4(平方厘米)
(2)3.14×(4.5÷2)2÷2≈7.9(平方厘米)
(3)5.5×1÷2≈2.8(平方厘米)
(4)4.5×1.5≈6.8(平方厘米)]
第四环节:综合提高性练习。(供学有余力的学生解答)
1.求下图阴影部分面积。(单位:厘米)
[提示:(1)把②移到靠近①处,便组成一个正方形,而阴影部分则是一个小长方形。解:3×(5-3)=6(平方厘米)
(2)解:求大小正方形面积和:52+32=34(平方厘米)
求大正方形面积的一半:52÷2=12.5(平方厘米)
求三角形面积:(5+3)×3÷2=12(平方厘米)
求阴影面积:34-12.5-12=9.5(平方厘米)]
第五环节:布置作业。(略)
同课章节目录
