西藏昌都市第一重点高中2021-2022学年高二上学期第一次月考数学试题(Word版含答案)
文档属性
| 名称 | 西藏昌都市第一重点高中2021-2022学年高二上学期第一次月考数学试题(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 415.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览




文档简介
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
昌都一高2020-2021学年度高二数学上期第一次月考试卷
考试时间:120分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题
1.设全集为实数集,集含,,则(
)
A.
B.
C.
D.
2.若a=0.22,b=30.5,c=log0.53,则a,b,c的大小关系是(
)
A.aB.cC.bD.c3.某几何体的三视图如图所示,则该几何体是(
)
A.圆柱
B.三棱台
C.圆台
D.圆锥
4.在中,角A,B,C所对边分别为a,b,c,若,则b等于(
)
A.3
B.6
C.2
D.4
5.在等差数列中,若,则(
)
A.20
B.24
C.27
D.29
6.的内角A,B,C的对边分别为,,.若,则为(
)
A.等腰且直角三角形
B.等腰或直角三角形
C.等边三角形
D.等腰三角形
7.设等差数列的前项和为,若,,则(
)
A.20
B.10
C.40
D.30
8.等比数列中,,,则数列的前6项和为(
)
A.21
B.
C.
D.11
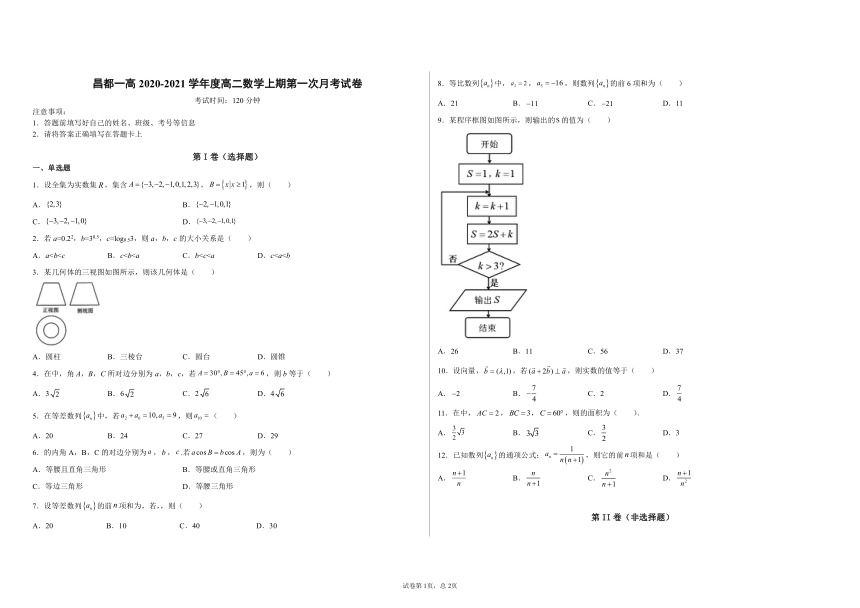
9.某程序框图如图所示,则输出的的值为(
)
A.26
B.11
C.56
D.37
10.设向量,,若,则实数的值等于(
)
A.
B.
C.2
D.
11.在中,,,,则的面积为(
).
A.
B.
C.
D.3
12.已知数列的通项公式:,则它的前项和是(
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题
13.中,,,则________.
14.设等差数列的前项和为,已知,,则_______.
15.等比数列2,6,…,的前10项和的值为______
16.已知等差数列中,,,那么等差数列的通项公式为___________.
三、解答题
17.已知等差数列{an}满足:a4=7,a10=19,其前n项和为Sn.求数列{an}的通项公式an及Sn.
18.已知函数y=
Asin(x+)(A>0,>0,||<)在一个周期上的图象如图所示.求这个函数的解析式.
19.在各项均为正数的等比数列{an}中,已知,求:
(1)a1与公比q的值;
(2)数列前6项的和S6
.
20.在正项等比数列中,,且,的等差中项为.
(1)求数列的通项公式;
(2)求数列的前项和为.
21.已知的内角,,的对边分别为,,,若.
(1)求角.
(2)若,求的面积.
22.我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照,…分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.
(3)估计居民月均用水量的中位数.
试卷第2页,总2页
试卷第1页,总1页
参考答案
1.C
【分析】
利用集合的交、补运算,求即可.
【详解】
由题设,,
∴.
故选:C
2.D
【分析】
利用指数函数、对数函数的单调性即可求解.
【详解】
,
,
,
所以.
故选:D
3.C
【分析】
由已知,得到几何体为旋转体,结合俯视图得到几何体是圆台.
【详解】
解:由俯视图得到几何体为圆台;
故选:C.
4.B
【分析】
直接利用正弦定理求解即可
【详解】
因为,
所以由正弦定理得,
,
所以,得,
故选:B
5.D
【分析】
求出基本量,即可求解.
【详解】
解:,所以,又,所以,
所以,
故选:D
6.C
【分析】
由等比数列的通项公式可得,即可解出答案.
【详解】
在等比数列,由
可得
解得
故选:C
7.D
【分析】
根据等差数列的性质可知,,构成等差数列,从而得到,进一步求出的值.
【详解】
解:由是等差数列,得,,构成等差数列,
所以,
所以,
解得.
故选:D.
8.A
【分析】
求出公比,再利用公式可求前6项的和.
【详解】
因为,故,故,
所以,故前6项和为.
故选:A.
9.A
【分析】
直接运行程序框图即可求解.
【详解】
由图知:初始值,
第一次循环,,,不成立,
第二次循环,,,不成立,
第三次循环,,,成立,
退出循环,输出的值为,
故选:A.
10.B
【分析】
由向量线性运算的坐标表示求的坐标,再由向量垂直的坐标表示求参数.
【详解】
由题设,,又,
∴,解得.
故选:B
11.A
【分析】
由已知利用三角形的面积公式即可求解.
【详解】
解:因为,,,
所以的面积.
故选:A.
12.B
【分析】
利用裂项相消法可求得结果.
【详解】
,
其前项和.
故选:B.
【点睛】
方法点睛:本题重点考查了裂项相消法求解数列的前项和的问题,裂项相消法适用于通项公式为形式的数列,即,进而前后相消求得结果.
13.6
【分析】
结合正弦定理求得正确结果.
【详解】
设的外接圆半径为,则.
则.
故答案为:
14.
【解析】
试题分析:根据等差数列的性质,可知成等差数列,即,解得.
考点:等差数列的性质.
15.59048
【分析】
根据给定条件算出等比数列公比,再用等比数列前n项和公式计算即得.
【详解】
依题意,给定等比数列首项为2,公比为3,
则前10项和为.
故答案为:59048
16.
【分析】
根据已知条件求得,由此求得.
【详解】
依题意.
故答案为:
17.,
【分析】
由已知可得,解方程组求出,从而可求得等差数列{an}的通项公式an及Sn.
【详解】
设等差数列的首项为,公差为,则,解得,,
∴.
18.
【分析】
通过图象的最高点或最低点可以直接求出,结合函数相邻零点求出(为函数的最小正周期),最后利用正弦型函数最小正周期公式求出,最后把其中一个点的坐标代入函数解析式中求出的值,最后写出正弦型函数的解析式.
【详解】
由图像知,.
设函数的最小正周期为,,,
,,
所以
把点代入解析式中有:
由,
,
所以函数的解析式为:.
19.(1);(2)63.
【分析】
(1)由已知得,解方程组可得;
(2)把所求与代入等比数列的求和公式化简可得.
【详解】
(1)由已知得,解得
(2)由求和公式可得
20.(1);(2).
【分析】
(1)设出公比,根据条件列方程组求解即可;
(2)分组,利用等差等比的求和公式求和.
【详解】
解(1)设正项等比数列的公比为,
由题意可得,解得.
数列的通项公式为;
(2).
【点睛】
本题考查等比数列的通项公式,考查等差,等比数列求和公式,是基础题.
21.(1);(2).
【分析】
(1)由正弦定理边角关系,结合三角形内角性质得,进而求角.
(2)由余弦定理得求b,再利用三角形面积公式求△的面积.
【详解】
(1)由正弦定理,,又,
,即,由,得.
(2)由余弦定理知:,
∴,解得,
.
22.(1);(2)万;(3).
【分析】
(1)由各组的频率和为1,列方程可求出的值,
(2)由频率分布直方图求出月均用水量不低于3吨的频率,再乘以总数可求得答案,
(3)由于前4组的频率小于,前5组的频率和大于,由此可得中位数在第5组,从而可求出中位数
【详解】
解:(1)∵,
整理可得:,∴解得:.
(2)由已知中的频率分布直方图可得月均用水量不低于3吨的频率为,又样本容量为30万,
则样本中月均用水量不低于3吨的户数为万.
(3)根据频率分布直方图,得;,,
∴中位数应在组内,设出未知数x,
令,
解得;∴中位数是.
答案第8页,总8页
答案第7页,总8页
昌都一高2020-2021学年度高二数学上期第一次月考试卷
考试时间:120分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题
1.设全集为实数集,集含,,则(
)
A.
B.
C.
D.
2.若a=0.22,b=30.5,c=log0.53,则a,b,c的大小关系是(
)
A.a
)
A.圆柱
B.三棱台
C.圆台
D.圆锥
4.在中,角A,B,C所对边分别为a,b,c,若,则b等于(
)
A.3
B.6
C.2
D.4
5.在等差数列中,若,则(
)
A.20
B.24
C.27
D.29
6.的内角A,B,C的对边分别为,,.若,则为(
)
A.等腰且直角三角形
B.等腰或直角三角形
C.等边三角形
D.等腰三角形
7.设等差数列的前项和为,若,,则(
)
A.20
B.10
C.40
D.30
8.等比数列中,,,则数列的前6项和为(
)
A.21
B.
C.
D.11
9.某程序框图如图所示,则输出的的值为(
)
A.26
B.11
C.56
D.37
10.设向量,,若,则实数的值等于(
)
A.
B.
C.2
D.
11.在中,,,,则的面积为(
).
A.
B.
C.
D.3
12.已知数列的通项公式:,则它的前项和是(
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题
13.中,,,则________.
14.设等差数列的前项和为,已知,,则_______.
15.等比数列2,6,…,的前10项和的值为______
16.已知等差数列中,,,那么等差数列的通项公式为___________.
三、解答题
17.已知等差数列{an}满足:a4=7,a10=19,其前n项和为Sn.求数列{an}的通项公式an及Sn.
18.已知函数y=
Asin(x+)(A>0,>0,||<)在一个周期上的图象如图所示.求这个函数的解析式.
19.在各项均为正数的等比数列{an}中,已知,求:
(1)a1与公比q的值;
(2)数列前6项的和S6
.
20.在正项等比数列中,,且,的等差中项为.
(1)求数列的通项公式;
(2)求数列的前项和为.
21.已知的内角,,的对边分别为,,,若.
(1)求角.
(2)若,求的面积.
22.我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照,…分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.
(3)估计居民月均用水量的中位数.
试卷第2页,总2页
试卷第1页,总1页
参考答案
1.C
【分析】
利用集合的交、补运算,求即可.
【详解】
由题设,,
∴.
故选:C
2.D
【分析】
利用指数函数、对数函数的单调性即可求解.
【详解】
,
,
,
所以.
故选:D
3.C
【分析】
由已知,得到几何体为旋转体,结合俯视图得到几何体是圆台.
【详解】
解:由俯视图得到几何体为圆台;
故选:C.
4.B
【分析】
直接利用正弦定理求解即可
【详解】
因为,
所以由正弦定理得,
,
所以,得,
故选:B
5.D
【分析】
求出基本量,即可求解.
【详解】
解:,所以,又,所以,
所以,
故选:D
6.C
【分析】
由等比数列的通项公式可得,即可解出答案.
【详解】
在等比数列,由
可得
解得
故选:C
7.D
【分析】
根据等差数列的性质可知,,构成等差数列,从而得到,进一步求出的值.
【详解】
解:由是等差数列,得,,构成等差数列,
所以,
所以,
解得.
故选:D.
8.A
【分析】
求出公比,再利用公式可求前6项的和.
【详解】
因为,故,故,
所以,故前6项和为.
故选:A.
9.A
【分析】
直接运行程序框图即可求解.
【详解】
由图知:初始值,
第一次循环,,,不成立,
第二次循环,,,不成立,
第三次循环,,,成立,
退出循环,输出的值为,
故选:A.
10.B
【分析】
由向量线性运算的坐标表示求的坐标,再由向量垂直的坐标表示求参数.
【详解】
由题设,,又,
∴,解得.
故选:B
11.A
【分析】
由已知利用三角形的面积公式即可求解.
【详解】
解:因为,,,
所以的面积.
故选:A.
12.B
【分析】
利用裂项相消法可求得结果.
【详解】
,
其前项和.
故选:B.
【点睛】
方法点睛:本题重点考查了裂项相消法求解数列的前项和的问题,裂项相消法适用于通项公式为形式的数列,即,进而前后相消求得结果.
13.6
【分析】
结合正弦定理求得正确结果.
【详解】
设的外接圆半径为,则.
则.
故答案为:
14.
【解析】
试题分析:根据等差数列的性质,可知成等差数列,即,解得.
考点:等差数列的性质.
15.59048
【分析】
根据给定条件算出等比数列公比,再用等比数列前n项和公式计算即得.
【详解】
依题意,给定等比数列首项为2,公比为3,
则前10项和为.
故答案为:59048
16.
【分析】
根据已知条件求得,由此求得.
【详解】
依题意.
故答案为:
17.,
【分析】
由已知可得,解方程组求出,从而可求得等差数列{an}的通项公式an及Sn.
【详解】
设等差数列的首项为,公差为,则,解得,,
∴.
18.
【分析】
通过图象的最高点或最低点可以直接求出,结合函数相邻零点求出(为函数的最小正周期),最后利用正弦型函数最小正周期公式求出,最后把其中一个点的坐标代入函数解析式中求出的值,最后写出正弦型函数的解析式.
【详解】
由图像知,.
设函数的最小正周期为,,,
,,
所以
把点代入解析式中有:
由,
,
所以函数的解析式为:.
19.(1);(2)63.
【分析】
(1)由已知得,解方程组可得;
(2)把所求与代入等比数列的求和公式化简可得.
【详解】
(1)由已知得,解得
(2)由求和公式可得
20.(1);(2).
【分析】
(1)设出公比,根据条件列方程组求解即可;
(2)分组,利用等差等比的求和公式求和.
【详解】
解(1)设正项等比数列的公比为,
由题意可得,解得.
数列的通项公式为;
(2).
【点睛】
本题考查等比数列的通项公式,考查等差,等比数列求和公式,是基础题.
21.(1);(2).
【分析】
(1)由正弦定理边角关系,结合三角形内角性质得,进而求角.
(2)由余弦定理得求b,再利用三角形面积公式求△的面积.
【详解】
(1)由正弦定理,,又,
,即,由,得.
(2)由余弦定理知:,
∴,解得,
.
22.(1);(2)万;(3).
【分析】
(1)由各组的频率和为1,列方程可求出的值,
(2)由频率分布直方图求出月均用水量不低于3吨的频率,再乘以总数可求得答案,
(3)由于前4组的频率小于,前5组的频率和大于,由此可得中位数在第5组,从而可求出中位数
【详解】
解:(1)∵,
整理可得:,∴解得:.
(2)由已知中的频率分布直方图可得月均用水量不低于3吨的频率为,又样本容量为30万,
则样本中月均用水量不低于3吨的户数为万.
(3)根据频率分布直方图,得;,,
∴中位数应在组内,设出未知数x,
令,
解得;∴中位数是.
答案第8页,总8页
答案第7页,总8页
同课章节目录
