23.2 中心对称同步课时训练 2021—2022学年人教版九年级数学上册 (Word版 含答案)
文档属性
| 名称 | 23.2 中心对称同步课时训练 2021—2022学年人教版九年级数学上册 (Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 696.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览





文档简介
人教版
九年级数学上册
23.2
中心对称
同步课时训练
一、选择题
1.
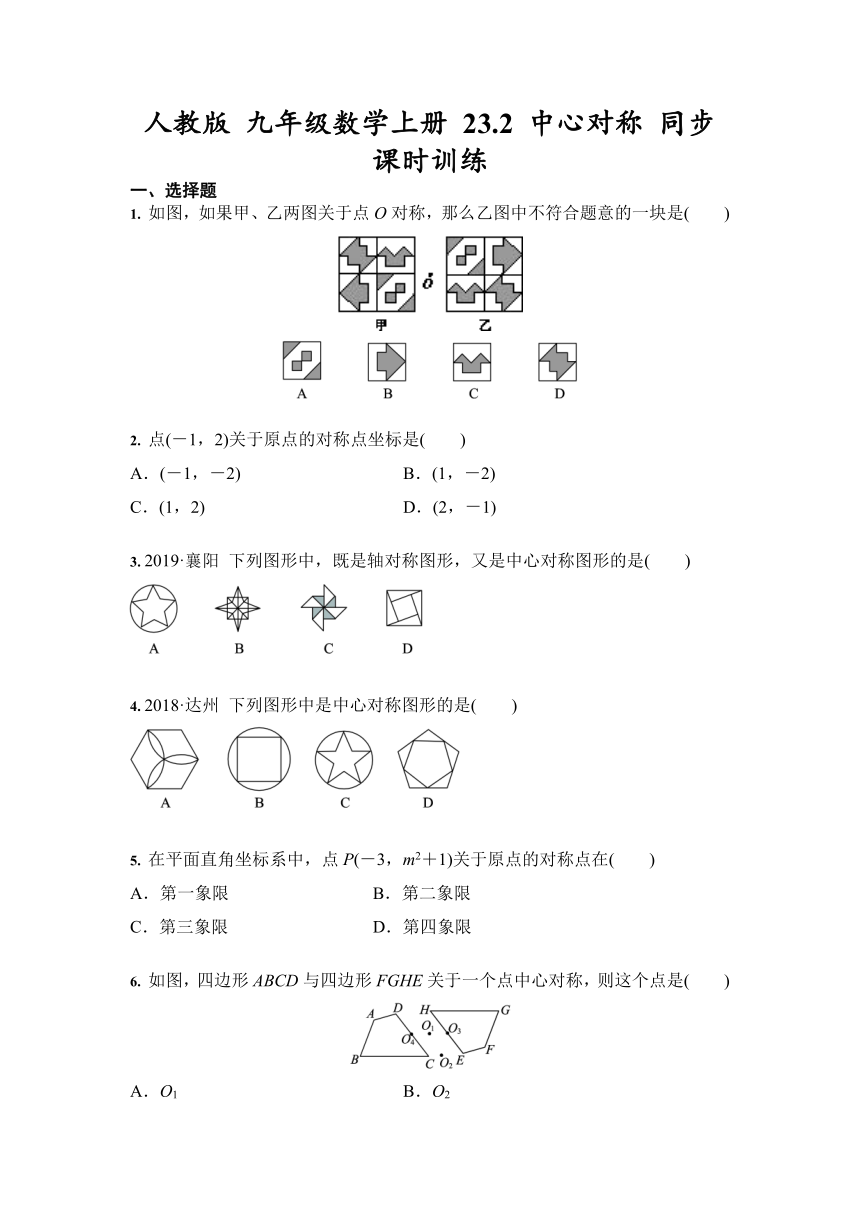
如图,如果甲、乙两图关于点O对称,那么乙图中不符合题意的一块是( )
2.
点(-1,2)关于原点的对称点坐标是( )
A.(-1,-2)
B.(1,-2)
C.(1,2)
D.(2,-1)
3.
2019·襄阳
下列图形中,既是轴对称图形,又是中心对称图形的是( )
4.
2018·达州
下列图形中是中心对称图形的是( )
5.
在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.
如图,四边形ABCD与四边形FGHE关于一个点中心对称,则这个点是( )
A.O1
B.O2
C.O3
D.O4
7.
在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1对称,再作△B2A3B3与△B2A2B1关于点B2对称……如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A.(4n-1,)
B.(2n-1,)
C.(4n+1,)
D.(2n+1,)
8.
2020·河北模拟
如图所示,A1(1,),A2(,),A3(2,),A4(3,0).作折线OA1A2A3A4关于点A4中心对称的图形,得折线A8A7A6A5A4,再作折线A8A7A6A5A4关于点A8中心对称的图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线以每秒1个单位长度的速度运动,设运动时间为t秒.当t=2020时,点P的坐标为( )
A.(1010,)
B.(2020,)
C.(2016,0)
D.(1010,)
二、填空题
9.
王老师、杨老师两家所在的位置关于学校对称.如果王老师家距学校2千米,那么他们两家相距________千米.
10.
如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,∠BAC≠90°.将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个四边形,则能拼出______个中心对称图形.
11.
如图所示,在△ABC中,已知∠ACB=90°,AC=BC=2.若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=________.
12.
若将等腰直角三角形AOB按图所示的方式放置,OB=2,则点A关于原点对称的点的坐标为________.
13.
已知?ABCD的顶点A在第三象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2.若点A的坐标为(a,b),则点D的坐标为________________.
14.
如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为________.
15.
2019·呼和浩特
已知正方形的对称中心在坐标原点,顶点A,B,C,D按逆时针依次排列,若点A的坐标为(2,),则点B与点D的坐标分别为( )
A.(-2,),(2,-)
B.(-,2),(,-2)
C.(-,2),(2,-)
D.(-,),(,-)
16.
如图,在平面直角坐标系中,对点P(1,0)作如下变换:先向上平移(后一次平移比前一次多1个单位长度),再作关于原点的对称点,即向上平移1个单位长度得到点P1,作点P1关于原点的对称点P2,向上平移2个单位长度得到点P3,作点P3关于原点的对称点P4……那么点P2020的坐标为____________.
三、作图题
17.
图①②都是由边长为1的小等边三角形构成的网格,每个网格中有5个小等边三角形已涂上阴影,请在余下的空白小等边三角形中,按下列要求选取一个涂上阴影:
(1)使得6个阴影小等边三角形组成一个轴对称图形;
(2)使得6个阴影小等边三角形组成一个中心对称图形.
(请将两个小题依次作答在图①②中,均只需画出符合条件的一种情形)
18.
探究题已知:如图①,四边形ABCD是中心对称图形,过对称中心O作直线EF分别交DC,AB于点E,F.
(1)如图①,四边形AFED与四边形CEFB的形状________,大小________;
(2)判断:经过中心对称图形的对称中心的任一条直线把这个图形分成面积相等的两个图形;( )
(3)你能否画一条直线,把图②中的平行四边形和圆同时分成形状相同、大小相等的两部分?
四、解答题
19.
如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称.已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
20.
如图,在正方形网格中,△ABC的三个顶点都在格点上,点A,B,C的坐标分别为(-2,4),(-2,0),(-4,1),结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC关于原点O对称的△A1B1C1;
(2)平移△ABC,使点A移动到点A2(0,2)的位置,画出平移后的△A2B2C2,并写出点B2,C2的坐标;
(3)在△ABC,△A1B1C1中,△A2B2C2与________成中心对称,其对称中心的坐标为________.
21.
2018·眉山
在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标;
(3)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
22.
[材料阅读]在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为.
[运用](1)已知点A(-2,1)和点B(4,-3),则线段AB的中点坐标是________;已知点M(2,3),线段MN的中点坐标是(-2,-1),则点N的坐标是________.
(2)已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6).直线y=mx-3m+2将四边形ABCD分成面积相等的两部分,则m的值为________.
(3)在平面直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D,可使以点A,B,C,D为顶点的四边形为平行四边形,求点D的坐标.
人教版
九年级数学上册
23.2
中心对称
同步课时训练-答案
一、选择题
1.
【答案】C [解析]
乙图中左下角的一块应为.
2.
【答案】B
3.
【答案】B
4.
【答案】B
5.
【答案】D
6.
【答案】A [解析]
如图,连接HC和DE交于点O1.
7.
【答案】C [解析]
A1(1,),A2(3,-),A3(5,),A4(7,-),…,
∴点An的坐标为
∵2n+1是奇数,∴点A2n+1的坐标是(4n+1,).故选C.
8.
【答案】A
二、填空题
9.
【答案】4 [解析]
∵王老师、杨老师两家所在的位置关于学校对称,
∴王老师、杨老师两家到学校的距离相等.
∵王老师家距学校2千米,
∴他们两家相距4千米.
故答案为4.
10.
【答案】3 [解析]
在这里具有中心对称图形特征的是平行四边形,所以两个三角形中对应相等的两
条边重合只能拼一个.因为三角形只有三条边,所以只有三种情况.
11.
【答案】2
[解析]
∵△ABC绕AC的中点O旋转了180°,
∴OB=OB′,∴BB′=2OB.
又∵OC=OA=AC=1,BC=2,
∴在Rt△OBC中,OB===,
∴BB′=2OB=2
.
12.
【答案】(-1,-1) [解析]
如图,过点A作AD⊥OB于点D.∵△AOB是等腰直角三角形,OB=2,∴OD=AD=1,∴A(1,1),∴点A关于原点对称的点的坐标为(-1,-1).
13.
【答案】(-2-a,-b)或(2-a,-b)
[解析]
如图①,∵点A的坐标为(a,b),AB与x轴平行,∴B(2+a,b).
∵点D与点B关于原点对称,∴D(-2-a,-b).
如图②,∵B(a-2,b),且点D与点B关于原点对称,∴D(2-a,-b).
14.
【答案】(0,1)
15.
【答案】B
16.
【答案】(1,-505)
[解析]
根据题意可列出下面的表格:
观察表格可知:这些点平均分布在四个象限中,序号除以4余1的点在第一象限,横坐标都是1,纵坐标为序号减1除以4的商加1;序号除以4余2的点是序号除以4余1的点关于原点的对称点;序号能被4整除的点在第四象限,横坐标为1,纵坐标为序号除以4的商的相反数;序号除以4余3的点在第二象限,是序号能被4整除的点关于原点的对称点.因为2020÷4=505,所以点P2020在第四象限,坐标为(1,-505).
三、作图题
17.
【答案】
解:(1)答案不唯一,画出下列其中一种即可.
(2)答案不唯一,画出下列其中一种即可.
18.
【答案】
(1)相同 相等 (2)√
(3)能.作经过平行四边形对角线交点和圆心O的直线即可,作图略.
四、解答题
19.
【答案】
解:(1)∵点D和点D1是对称点,
∴对称中心是线段DD1的中点,
∴对称中心的坐标是(0,).
(2)B(-2,4),C(-2,2),B1(2,1),C1(2,3).
20.
【答案】
解:(1)△ABC关于原点O对称的△A1B1C1如图所示.
(2)平移后的△A2B2C2如图所示,其中点B2的坐标为(0,-2),点C2的坐标为(-2,-1).
(3)△A1B1C1 (1,-1)
21.
【答案】
解:(1)如图,△A1B1C1为所作,C1(-1,2).
(2)如图,△A2B2C2为所作,C2(-3,-2).
(3)因为点A的坐标为(2,4),点A3的坐标为(-4,-2),
所以直线l的函数解析式为y=-x.
22.
【答案】
解:(1)(1,-1) (-6,-5)
(2)
(3)设点D的坐标为(x,y).
若以AB为对角线,AC,BC为邻边的四边形为平行四边形,则AB,CD的中点重合,
∴解得
若以BC为对角线,AB,AC为邻边的四边形为平行四边形,则AD,BC的中点重合,
∴
解得
若以AC为对角线,AB,BC为邻边的四边形为平行四边形,则BD,AC的中点重合,
∴
解得
综上可知,点D的坐标为(1,-1)或(5,3)或(-3,5).
九年级数学上册
23.2
中心对称
同步课时训练
一、选择题
1.
如图,如果甲、乙两图关于点O对称,那么乙图中不符合题意的一块是( )
2.
点(-1,2)关于原点的对称点坐标是( )
A.(-1,-2)
B.(1,-2)
C.(1,2)
D.(2,-1)
3.
2019·襄阳
下列图形中,既是轴对称图形,又是中心对称图形的是( )
4.
2018·达州
下列图形中是中心对称图形的是( )
5.
在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.
如图,四边形ABCD与四边形FGHE关于一个点中心对称,则这个点是( )
A.O1
B.O2
C.O3
D.O4
7.
在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1对称,再作△B2A3B3与△B2A2B1关于点B2对称……如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A.(4n-1,)
B.(2n-1,)
C.(4n+1,)
D.(2n+1,)
8.
2020·河北模拟
如图所示,A1(1,),A2(,),A3(2,),A4(3,0).作折线OA1A2A3A4关于点A4中心对称的图形,得折线A8A7A6A5A4,再作折线A8A7A6A5A4关于点A8中心对称的图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线以每秒1个单位长度的速度运动,设运动时间为t秒.当t=2020时,点P的坐标为( )
A.(1010,)
B.(2020,)
C.(2016,0)
D.(1010,)
二、填空题
9.
王老师、杨老师两家所在的位置关于学校对称.如果王老师家距学校2千米,那么他们两家相距________千米.
10.
如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,∠BAC≠90°.将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个四边形,则能拼出______个中心对称图形.
11.
如图所示,在△ABC中,已知∠ACB=90°,AC=BC=2.若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=________.
12.
若将等腰直角三角形AOB按图所示的方式放置,OB=2,则点A关于原点对称的点的坐标为________.
13.
已知?ABCD的顶点A在第三象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2.若点A的坐标为(a,b),则点D的坐标为________________.
14.
如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为________.
15.
2019·呼和浩特
已知正方形的对称中心在坐标原点,顶点A,B,C,D按逆时针依次排列,若点A的坐标为(2,),则点B与点D的坐标分别为( )
A.(-2,),(2,-)
B.(-,2),(,-2)
C.(-,2),(2,-)
D.(-,),(,-)
16.
如图,在平面直角坐标系中,对点P(1,0)作如下变换:先向上平移(后一次平移比前一次多1个单位长度),再作关于原点的对称点,即向上平移1个单位长度得到点P1,作点P1关于原点的对称点P2,向上平移2个单位长度得到点P3,作点P3关于原点的对称点P4……那么点P2020的坐标为____________.
三、作图题
17.
图①②都是由边长为1的小等边三角形构成的网格,每个网格中有5个小等边三角形已涂上阴影,请在余下的空白小等边三角形中,按下列要求选取一个涂上阴影:
(1)使得6个阴影小等边三角形组成一个轴对称图形;
(2)使得6个阴影小等边三角形组成一个中心对称图形.
(请将两个小题依次作答在图①②中,均只需画出符合条件的一种情形)
18.
探究题已知:如图①,四边形ABCD是中心对称图形,过对称中心O作直线EF分别交DC,AB于点E,F.
(1)如图①,四边形AFED与四边形CEFB的形状________,大小________;
(2)判断:经过中心对称图形的对称中心的任一条直线把这个图形分成面积相等的两个图形;( )
(3)你能否画一条直线,把图②中的平行四边形和圆同时分成形状相同、大小相等的两部分?
四、解答题
19.
如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称.已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
20.
如图,在正方形网格中,△ABC的三个顶点都在格点上,点A,B,C的坐标分别为(-2,4),(-2,0),(-4,1),结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC关于原点O对称的△A1B1C1;
(2)平移△ABC,使点A移动到点A2(0,2)的位置,画出平移后的△A2B2C2,并写出点B2,C2的坐标;
(3)在△ABC,△A1B1C1中,△A2B2C2与________成中心对称,其对称中心的坐标为________.
21.
2018·眉山
在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标;
(3)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
22.
[材料阅读]在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为.
[运用](1)已知点A(-2,1)和点B(4,-3),则线段AB的中点坐标是________;已知点M(2,3),线段MN的中点坐标是(-2,-1),则点N的坐标是________.
(2)已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6).直线y=mx-3m+2将四边形ABCD分成面积相等的两部分,则m的值为________.
(3)在平面直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D,可使以点A,B,C,D为顶点的四边形为平行四边形,求点D的坐标.
人教版
九年级数学上册
23.2
中心对称
同步课时训练-答案
一、选择题
1.
【答案】C [解析]
乙图中左下角的一块应为.
2.
【答案】B
3.
【答案】B
4.
【答案】B
5.
【答案】D
6.
【答案】A [解析]
如图,连接HC和DE交于点O1.
7.
【答案】C [解析]
A1(1,),A2(3,-),A3(5,),A4(7,-),…,
∴点An的坐标为
∵2n+1是奇数,∴点A2n+1的坐标是(4n+1,).故选C.
8.
【答案】A
二、填空题
9.
【答案】4 [解析]
∵王老师、杨老师两家所在的位置关于学校对称,
∴王老师、杨老师两家到学校的距离相等.
∵王老师家距学校2千米,
∴他们两家相距4千米.
故答案为4.
10.
【答案】3 [解析]
在这里具有中心对称图形特征的是平行四边形,所以两个三角形中对应相等的两
条边重合只能拼一个.因为三角形只有三条边,所以只有三种情况.
11.
【答案】2
[解析]
∵△ABC绕AC的中点O旋转了180°,
∴OB=OB′,∴BB′=2OB.
又∵OC=OA=AC=1,BC=2,
∴在Rt△OBC中,OB===,
∴BB′=2OB=2
.
12.
【答案】(-1,-1) [解析]
如图,过点A作AD⊥OB于点D.∵△AOB是等腰直角三角形,OB=2,∴OD=AD=1,∴A(1,1),∴点A关于原点对称的点的坐标为(-1,-1).
13.
【答案】(-2-a,-b)或(2-a,-b)
[解析]
如图①,∵点A的坐标为(a,b),AB与x轴平行,∴B(2+a,b).
∵点D与点B关于原点对称,∴D(-2-a,-b).
如图②,∵B(a-2,b),且点D与点B关于原点对称,∴D(2-a,-b).
14.
【答案】(0,1)
15.
【答案】B
16.
【答案】(1,-505)
[解析]
根据题意可列出下面的表格:
观察表格可知:这些点平均分布在四个象限中,序号除以4余1的点在第一象限,横坐标都是1,纵坐标为序号减1除以4的商加1;序号除以4余2的点是序号除以4余1的点关于原点的对称点;序号能被4整除的点在第四象限,横坐标为1,纵坐标为序号除以4的商的相反数;序号除以4余3的点在第二象限,是序号能被4整除的点关于原点的对称点.因为2020÷4=505,所以点P2020在第四象限,坐标为(1,-505).
三、作图题
17.
【答案】
解:(1)答案不唯一,画出下列其中一种即可.
(2)答案不唯一,画出下列其中一种即可.
18.
【答案】
(1)相同 相等 (2)√
(3)能.作经过平行四边形对角线交点和圆心O的直线即可,作图略.
四、解答题
19.
【答案】
解:(1)∵点D和点D1是对称点,
∴对称中心是线段DD1的中点,
∴对称中心的坐标是(0,).
(2)B(-2,4),C(-2,2),B1(2,1),C1(2,3).
20.
【答案】
解:(1)△ABC关于原点O对称的△A1B1C1如图所示.
(2)平移后的△A2B2C2如图所示,其中点B2的坐标为(0,-2),点C2的坐标为(-2,-1).
(3)△A1B1C1 (1,-1)
21.
【答案】
解:(1)如图,△A1B1C1为所作,C1(-1,2).
(2)如图,△A2B2C2为所作,C2(-3,-2).
(3)因为点A的坐标为(2,4),点A3的坐标为(-4,-2),
所以直线l的函数解析式为y=-x.
22.
【答案】
解:(1)(1,-1) (-6,-5)
(2)
(3)设点D的坐标为(x,y).
若以AB为对角线,AC,BC为邻边的四边形为平行四边形,则AB,CD的中点重合,
∴解得
若以BC为对角线,AB,AC为邻边的四边形为平行四边形,则AD,BC的中点重合,
∴
解得
若以AC为对角线,AB,BC为邻边的四边形为平行四边形,则BD,AC的中点重合,
∴
解得
综上可知,点D的坐标为(1,-1)或(5,3)或(-3,5).
同课章节目录
