人教版九年级数学下册 27.1 图形的相似复习试题(Word版 含答案)
文档属性
| 名称 | 人教版九年级数学下册 27.1 图形的相似复习试题(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 218.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览




文档简介
27.1
图形的相似
一、选择题
1.
如图,下面右边的四个图形中,与左边的图形形状相同的是(
)
2.
如图,在矩形ABCD中,AB)
A.1个
B.2个
C.3个
D.4个
3.
如图,已知△ABC∽△DEF,
AB∶DE=1∶2,则下列等式一定成立的是(
)
A.=
B.=
C.=
D.=
4.
如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4∶9,则OB′∶OB为(
)
A.2∶3
B.3∶2
C.4∶5
D.4∶9
5.
如果线段a,b,c满足=,且b的长为3,c的长为12,那么a的长为(
)
A.3
B.5
C.6
D.9
6.
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为(
)
A.1.25尺
B.57.5尺
C.6.25尺
D.56.5尺
7.
两地实际距离是500
m,画在图上的距离是25
cm,若在此图上量得A,B两地相距40
cm,则A,B两地的实际距离是(
)
A.800m
B.8000m
C.32250m
D.3225m
8.下列各组线段(单位:cm)中,成比例的是(
)
A.1,2,3,4
B.1,2,2,4
C.3,5,9,13
D.1,2,2,3
9.
四边形ABCD的四条边长分别是2,3,4,5,如果与其相似的四边形A′B′C′D′的最长边长为15,那么四边形A′B′C′D′的最短边长为(
)
A.6
B.5
C.4
D.3
10.如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连结EG交AC于点H,若点H是AC的中点,则的值为(
)
A.
4∶3
B.
4∶2
C.
4∶1
D.
3∶2
二、填空题
11.
已知=,则的值是________.
12.
如图所示的两个五边形相似,未知边a=______,b=______,c=______,d=______.
13.
一个铝质三角形框架三条边长分别为24
cm,30
cm,36
cm,要做一个与它相似的铝质三角形框架,现有长为27
cm,45
cm的两根铝材,要求以其中一根为一边,从另一根上截下两段(允许有余)作为另外两边,截法有_____种.
14.
如图所示的两个直角三角形相似因为它们的对应角___,对应边的比___.
15.
在比例尺为1∶10
000
000的地图上,量得甲、乙两地的距离是30
cm,z\则两地的实际距离为______
km.
16.
如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1∶3,则点B的对应点B′的坐标为____.
17.
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为____尺.
18.
一张桌面长a=1.25
m,宽b=0.75
m,那么长与宽的比是_____.
19.
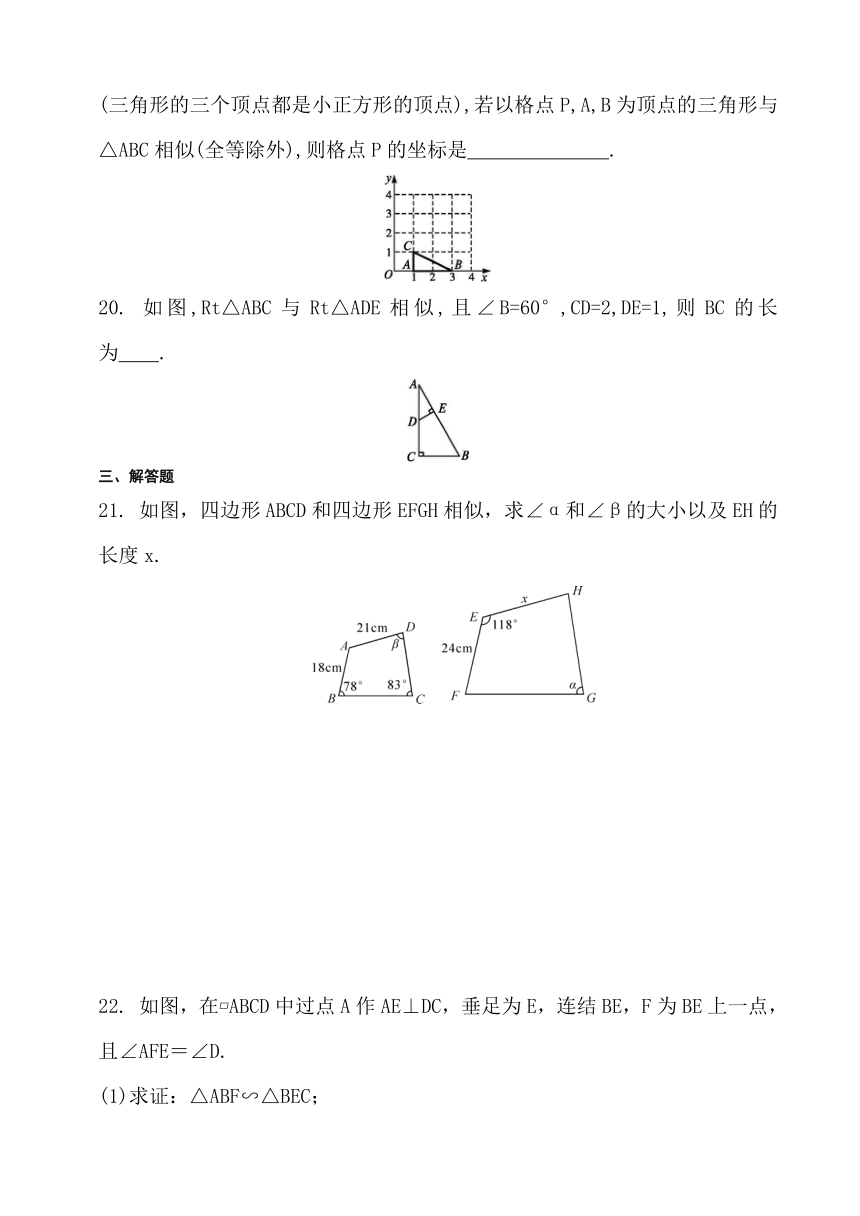
如图,在已建立直角坐标系的4×4正方形方格纸中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点),若以格点P,A,B为顶点的三角形与△ABC相似(全等除外),则格点P的坐标是
.
20.
如图,Rt△ABC与Rt△ADE相似,且∠B=60°,CD=2,DE=1,则BC的长为
.
三、解答题
21.
如图,四边形ABCD和四边形EFGH相似,求∠α和∠β的大小以及EH的长度x.
22.
如图,在?ABCD中过点A作AE⊥DC,垂足为E,连结BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=,求AF的长.
23.
如图,在矩形ABCD中,AB=2AD,线段EF=10,在EF上取一点M,分别以EM,MF为一边作矩形EMNH,MFGN,使矩形MFGN与矩形ABCD相似(MF与AB是对应边),令MN=x,当x为何值时,矩形EMNH的面积S有最大值?最大值是多少?
24.
如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是多少?
25.
.如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.求:
(1)AD的长;
(2)矩形DMNC与矩形ABCD的相似比.
26.
某矩形场地长20,宽16.
(1)
如图①,在场地中央建有一矩形草坪,沿草坪四周外围有宽为x的环形小路,小路内外边缘所成的矩形相似吗?
(2)
如果它们的位置变为图②中的位置,它们能相似吗?若能相似,求出x,y满足的关系.
27.
如图分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图①所示的图形,AF经过点C,连结DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连结BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图②,在(1)的前提下,当∠ABE=135°时,延长AD,EF交于点N,求的值;
(3)在(2)的条件下,若=k(k为大于的常数),直接用含k的代数式表示的值.
答案:
1---10
CBDAC
BABAA
11.
12.
3
4
6.
13.
1
14.
相等
相等
15.
3000
16.
(-8,-3)或(4,3)
17.
57.5
18.
19.
(1,4)或(3,4)
20.
21.
解:四边形ABCD和四边形EFGH相似,它们的对应角相等.由此可得
∠α=∠C=83°,∠A=∠E=118°,
在四边形ABCD中,
∠β=360°-(78°+83°+118°)
=81°.
四边形ABCD和四边形EFGH相似,它们的对应边成比例.由此可得
=,即=.
解得x=28cm.
22.
解:(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
AD=BC,∴∠D+∠C=180°,∠ABF=∠BEC,∵AFB+∠AFE=180°,
∴∠C=∠AFB,∴△ABF∽△BEC.
(2)∵AE⊥DC,AB∥DC,∴∠AED=∠BAE=90°.在Rt△ADE中,
AE=AD·sinD=5×=4,在Rt△ABE中,
根据勾股定理,得BE===4.
∵△ABF∽△BEC,=,即=,
解得AF=2.
23.
解:∵矩形MFGN和矩形ABCD相似,∴==2.
∵MN=x,∴MF=2x,∴EM=EF-MF=10-2x,
∴S=x(10-2x)=-2x2+10x=-2+.
∴当x=时,S有最大值.
24.
解:∵△ABC与△DEC的面积相等,∴△CDF与四边形AFEB的面积相等,
∵AB∥DE,∴△CEF∽△CBA,∵EF=9,AB=12,∴EF∶AB=9∶12=3∶4,
∴△CEF和△CBA的面积比=9∶16,
设△CEF的面积为9k,则四边形AFEB的面积=7k,
∵△CDF与四边形AFEB的面积相等,∴S△CDF=7k,
∵△CDF与△CEF是同高不同底的三角形,∴面积比等于底之比,
∴DF∶EF=7k∶9k,∴DF=7.
25.
解(1)由已知,得MN=AB=4,MD=AD.
∵矩形DMNC与矩形ABCD相似,∴,∴AD2=16,AD=4.
(2)由(1)知,DM=AD=2,则矩形DMNC与矩形ABCD的相似比为.
26.
解:(1)∵AB=CD=20,AD=BC=16,
∴EF=GH=20-2x,EH=FG=16-2x.
∴==1-,==1-.
∵≠,∴≠.
∴小路内外边缘所成的矩形不相似.
(2)图②中的两个矩形可以相似,相似时x,y满足的关系如下:
①=,解得y=x(0<x<20).
②=,解得y=x-9(7.2<x<20),
即当y=x(0<x<20)或y=x-9(7.2<x<20)时,两个矩形相似.
27.
解:(1)证明:∵四边形ABCD是菱形,∴AB=CD,AB∥CD,
∵四边形ABEF是平行四边形,∴AB=EF,AB∥EF,∴CD=EF,CD∥EF,
∴∠CDM=∠FEM,在△CDM和△FEM中,
∴△CDM≌△FEM,∴DM=EM,即点M是DE的中点.
(2)∵△CDM≌△FEM,∴CM=FM.设AD=a,CM=b.∵∠ABE=135°,
∴∠BAF=45°.∵四边形ABCD为菱形,∴∠NAF=45°,∴∠DAB=90°,
∴四边形ABCD为正方形,∴AC=AD=a.∵AB∥EF,
∴∠AFN=∠BAF=45°,∴△ANF为等腰直角三角形,
∴NF=AF=(a+b+b)=a+b,
∴NE=NF+EF=a+b+a=2a+b,
∴===.
(3)∵==+2·=k,∴=(k-),∴=,
∴==·+1=·+1=.
图形的相似
一、选择题
1.
如图,下面右边的四个图形中,与左边的图形形状相同的是(
)
2.
如图,在矩形ABCD中,AB
A.1个
B.2个
C.3个
D.4个
3.
如图,已知△ABC∽△DEF,
AB∶DE=1∶2,则下列等式一定成立的是(
)
A.=
B.=
C.=
D.=
4.
如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4∶9,则OB′∶OB为(
)
A.2∶3
B.3∶2
C.4∶5
D.4∶9
5.
如果线段a,b,c满足=,且b的长为3,c的长为12,那么a的长为(
)
A.3
B.5
C.6
D.9
6.
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为(
)
A.1.25尺
B.57.5尺
C.6.25尺
D.56.5尺
7.
两地实际距离是500
m,画在图上的距离是25
cm,若在此图上量得A,B两地相距40
cm,则A,B两地的实际距离是(
)
A.800m
B.8000m
C.32250m
D.3225m
8.下列各组线段(单位:cm)中,成比例的是(
)
A.1,2,3,4
B.1,2,2,4
C.3,5,9,13
D.1,2,2,3
9.
四边形ABCD的四条边长分别是2,3,4,5,如果与其相似的四边形A′B′C′D′的最长边长为15,那么四边形A′B′C′D′的最短边长为(
)
A.6
B.5
C.4
D.3
10.如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连结EG交AC于点H,若点H是AC的中点,则的值为(
)
A.
4∶3
B.
4∶2
C.
4∶1
D.
3∶2
二、填空题
11.
已知=,则的值是________.
12.
如图所示的两个五边形相似,未知边a=______,b=______,c=______,d=______.
13.
一个铝质三角形框架三条边长分别为24
cm,30
cm,36
cm,要做一个与它相似的铝质三角形框架,现有长为27
cm,45
cm的两根铝材,要求以其中一根为一边,从另一根上截下两段(允许有余)作为另外两边,截法有_____种.
14.
如图所示的两个直角三角形相似因为它们的对应角___,对应边的比___.
15.
在比例尺为1∶10
000
000的地图上,量得甲、乙两地的距离是30
cm,z\则两地的实际距离为______
km.
16.
如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1∶3,则点B的对应点B′的坐标为____.
17.
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为____尺.
18.
一张桌面长a=1.25
m,宽b=0.75
m,那么长与宽的比是_____.
19.
如图,在已建立直角坐标系的4×4正方形方格纸中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点),若以格点P,A,B为顶点的三角形与△ABC相似(全等除外),则格点P的坐标是
.
20.
如图,Rt△ABC与Rt△ADE相似,且∠B=60°,CD=2,DE=1,则BC的长为
.
三、解答题
21.
如图,四边形ABCD和四边形EFGH相似,求∠α和∠β的大小以及EH的长度x.
22.
如图,在?ABCD中过点A作AE⊥DC,垂足为E,连结BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=,求AF的长.
23.
如图,在矩形ABCD中,AB=2AD,线段EF=10,在EF上取一点M,分别以EM,MF为一边作矩形EMNH,MFGN,使矩形MFGN与矩形ABCD相似(MF与AB是对应边),令MN=x,当x为何值时,矩形EMNH的面积S有最大值?最大值是多少?
24.
如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是多少?
25.
.如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.求:
(1)AD的长;
(2)矩形DMNC与矩形ABCD的相似比.
26.
某矩形场地长20,宽16.
(1)
如图①,在场地中央建有一矩形草坪,沿草坪四周外围有宽为x的环形小路,小路内外边缘所成的矩形相似吗?
(2)
如果它们的位置变为图②中的位置,它们能相似吗?若能相似,求出x,y满足的关系.
27.
如图分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图①所示的图形,AF经过点C,连结DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连结BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图②,在(1)的前提下,当∠ABE=135°时,延长AD,EF交于点N,求的值;
(3)在(2)的条件下,若=k(k为大于的常数),直接用含k的代数式表示的值.
答案:
1---10
CBDAC
BABAA
11.
12.
3
4
6.
13.
1
14.
相等
相等
15.
3000
16.
(-8,-3)或(4,3)
17.
57.5
18.
19.
(1,4)或(3,4)
20.
21.
解:四边形ABCD和四边形EFGH相似,它们的对应角相等.由此可得
∠α=∠C=83°,∠A=∠E=118°,
在四边形ABCD中,
∠β=360°-(78°+83°+118°)
=81°.
四边形ABCD和四边形EFGH相似,它们的对应边成比例.由此可得
=,即=.
解得x=28cm.
22.
解:(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
AD=BC,∴∠D+∠C=180°,∠ABF=∠BEC,∵AFB+∠AFE=180°,
∴∠C=∠AFB,∴△ABF∽△BEC.
(2)∵AE⊥DC,AB∥DC,∴∠AED=∠BAE=90°.在Rt△ADE中,
AE=AD·sinD=5×=4,在Rt△ABE中,
根据勾股定理,得BE===4.
∵△ABF∽△BEC,=,即=,
解得AF=2.
23.
解:∵矩形MFGN和矩形ABCD相似,∴==2.
∵MN=x,∴MF=2x,∴EM=EF-MF=10-2x,
∴S=x(10-2x)=-2x2+10x=-2+.
∴当x=时,S有最大值.
24.
解:∵△ABC与△DEC的面积相等,∴△CDF与四边形AFEB的面积相等,
∵AB∥DE,∴△CEF∽△CBA,∵EF=9,AB=12,∴EF∶AB=9∶12=3∶4,
∴△CEF和△CBA的面积比=9∶16,
设△CEF的面积为9k,则四边形AFEB的面积=7k,
∵△CDF与四边形AFEB的面积相等,∴S△CDF=7k,
∵△CDF与△CEF是同高不同底的三角形,∴面积比等于底之比,
∴DF∶EF=7k∶9k,∴DF=7.
25.
解(1)由已知,得MN=AB=4,MD=AD.
∵矩形DMNC与矩形ABCD相似,∴,∴AD2=16,AD=4.
(2)由(1)知,DM=AD=2,则矩形DMNC与矩形ABCD的相似比为.
26.
解:(1)∵AB=CD=20,AD=BC=16,
∴EF=GH=20-2x,EH=FG=16-2x.
∴==1-,==1-.
∵≠,∴≠.
∴小路内外边缘所成的矩形不相似.
(2)图②中的两个矩形可以相似,相似时x,y满足的关系如下:
①=,解得y=x(0<x<20).
②=,解得y=x-9(7.2<x<20),
即当y=x(0<x<20)或y=x-9(7.2<x<20)时,两个矩形相似.
27.
解:(1)证明:∵四边形ABCD是菱形,∴AB=CD,AB∥CD,
∵四边形ABEF是平行四边形,∴AB=EF,AB∥EF,∴CD=EF,CD∥EF,
∴∠CDM=∠FEM,在△CDM和△FEM中,
∴△CDM≌△FEM,∴DM=EM,即点M是DE的中点.
(2)∵△CDM≌△FEM,∴CM=FM.设AD=a,CM=b.∵∠ABE=135°,
∴∠BAF=45°.∵四边形ABCD为菱形,∴∠NAF=45°,∴∠DAB=90°,
∴四边形ABCD为正方形,∴AC=AD=a.∵AB∥EF,
∴∠AFN=∠BAF=45°,∴△ANF为等腰直角三角形,
∴NF=AF=(a+b+b)=a+b,
∴NE=NF+EF=a+b+a=2a+b,
∴===.
(3)∵==+2·=k,∴=(k-),∴=,
∴==·+1=·+1=.
