2021-2022学年人教版数学八年级上册13.3.2 等边三角形 课件(22张)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册13.3.2 等边三角形 课件(22张) |
|
|
| 格式 | zip | ||
| 文件大小 | 207.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
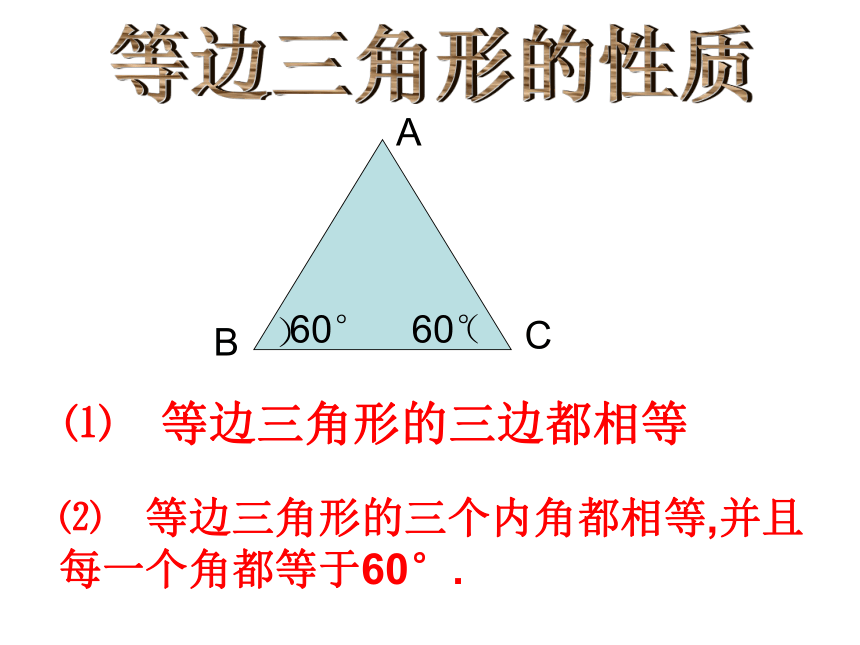
想想看,等边三角形
有什么性质?
A
B
C
⑴三边之间
AB_AC_BC
⑵三角之间
∠A_∠B_∠C
=
=
=
=
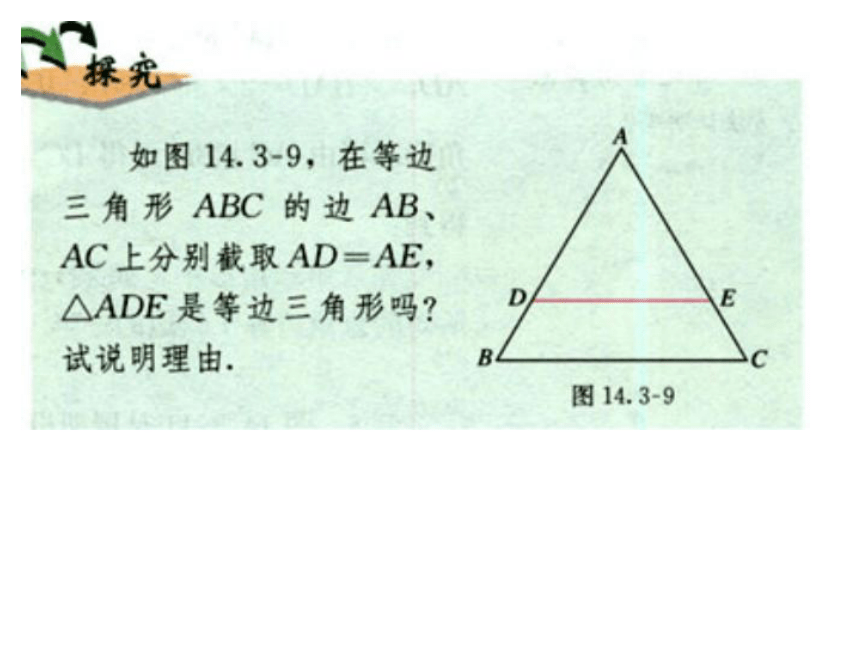
⑵ 等边三角形的三个内角都相等,并且
每一个角都等于60°.
等边三角形的性质
⑴ 等边三角形的三边都相等
A
B
C
)
(
60°
60°
思考题
?
一个三角形满足什么条件
就是等边三角形?
一般三角形
等边三角形
⒈
三个角都相等的三角形是等边三角形.
⒉
有一个角是60°的等腰三角形是等边
三角形.
等边三角形
等腰三角形
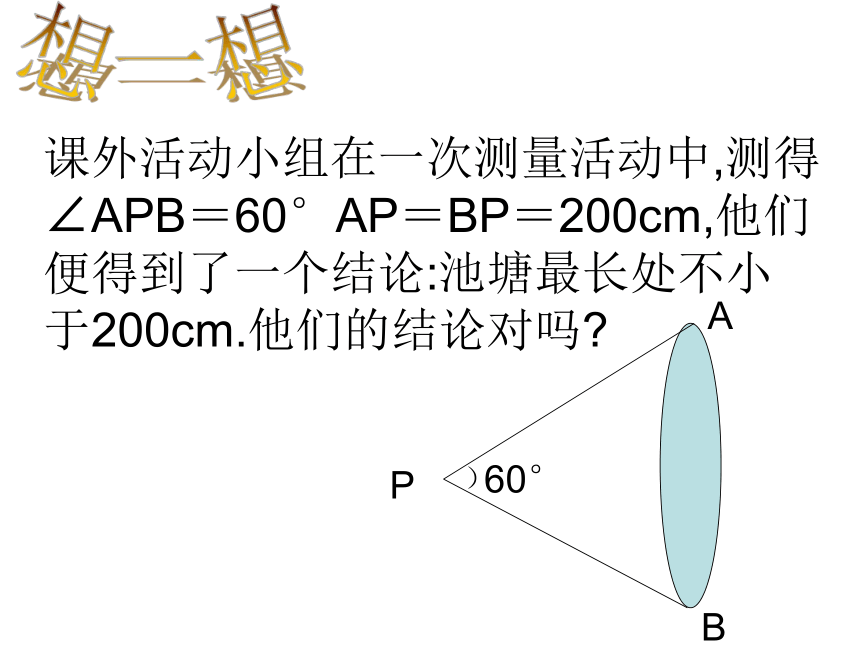
想一想
课外活动小组在一次测量活动中,测得
∠APB=60°AP=BP=200cm,他们
便得到了一个结论:池塘最长处不小
于200cm.他们的结论对吗?
)
60°
P
A
B
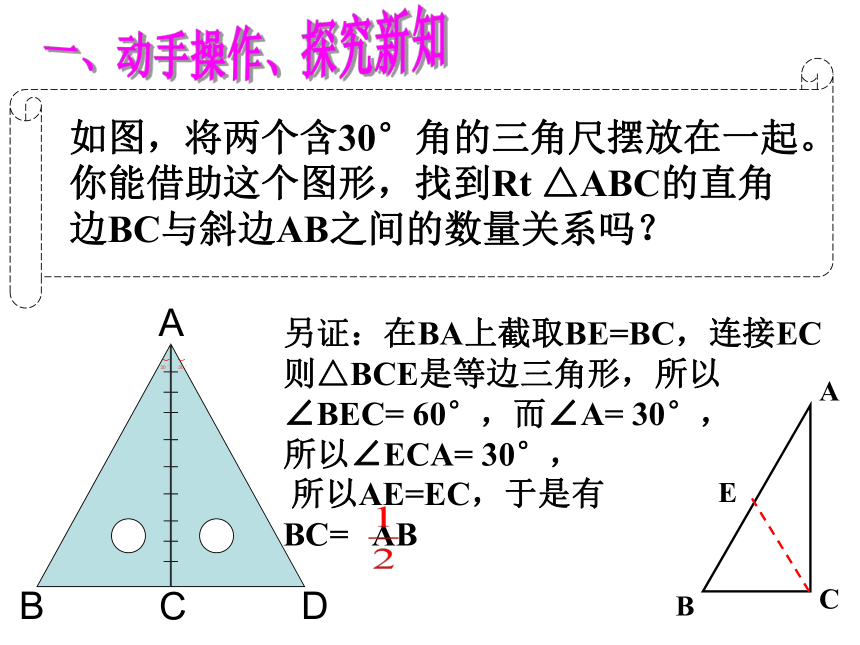
如图,将两个含30°角的三角尺摆放在一起。
你能借助这个图形,找到Rt
△ABC的直角
边BC与斜边AB之间的数量关系吗?
B
A
C
D
30
°
30
°
一、动手操作、探究新知
E
A
C
B
另证:在BA上截取BE=BC,连接EC
则△BCE是等边三角形,所以
∠BEC=
60°,而∠A=
30°,
所以∠ECA=
30°,
所以AE=EC,于是有
BC=
AB
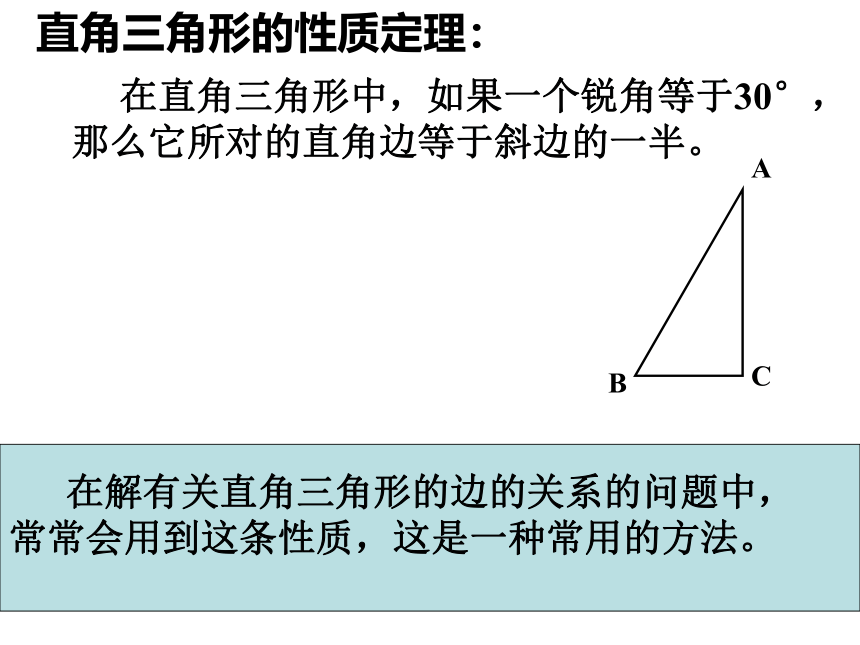
直角三角形的性质定理:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
A
C
B
在解有关直角三角形的边的关系的问题中,
常常会用到这条性质,这是一种常用的方法。
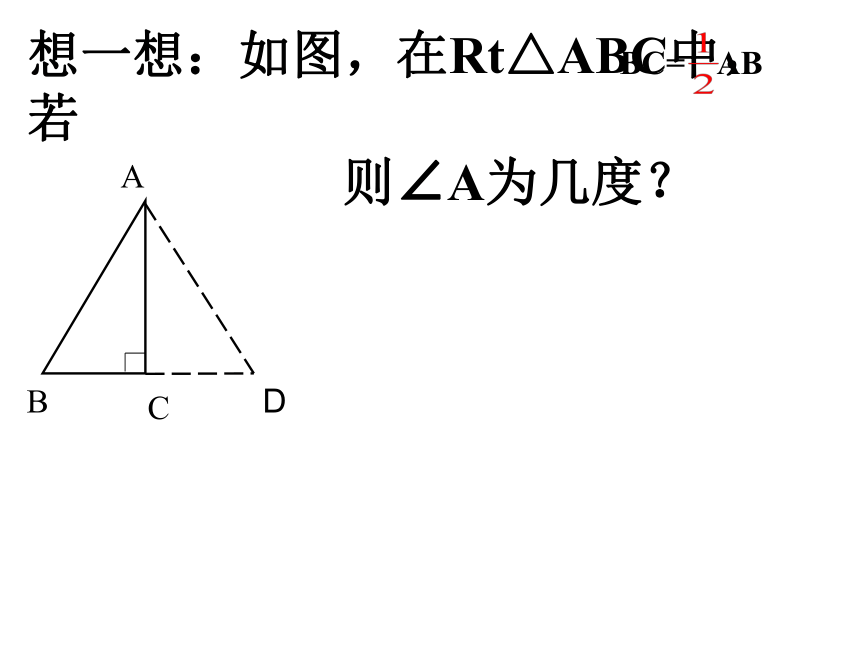
想一想:如图,在Rt△ABC中,若
则∠A为几度?
BC=
AB
A
C
B
D
下图是屋架设计图的一部分,点D是
斜梁AB的中点,立柱BC、
DE垂直于
横梁AC,AB=7.4m,∠A=30°立柱
BC
、
DE要多长?
A
B
D
E
C
解:∵DE⊥AC,
BC⊥AC,
∠A=30°
可得
2BC=AB,
2DE=AD
∴BC=1/2
×7.4=3.7m
又
AD=1/2
AB
∴DE=1/2
AD=1/2
×3.7=1.85m
答:立柱BC的长是3.7m,DE的长是
1.85m.
比一比:看
谁
算
的
快
1.如图:在Rt△ABC中
∠A=300,AB+BC=12cm
则AB=_____cm
C
B
A
300
8
2.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm, BD=___, BE=____
A
C
E
B
D
4cm
2cm
例题1.
如图在△ABC中,AB=AC=2a,∠ABC=∠ACB=150,CD是腰AB上的高,求CD的长
┏
D
C
B
A
解:∵∠ABC=∠ACB=150
∴∠DAC=∠ABC+∠ACB=300
∴CD=1/2AC=a
要把一块三角形的土地均匀分给甲
、
乙、丙三家农户去种植,如果∠C=90°∠B=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.
A
C
B
┓
请你分一分
A
B
C
D
如图,在△ABC中,∠BAC=90°,∠B=30°,AD⊥BC于D。求证:BC=4CD
如图,
∠AOB=
30°,P是角平分线上的点,
PM⊥OB于M,PN//OB交OA于N,若PM=1cm,
则PN=________.
2cm
A
N
M
P
B
O
E
一、回顾与反思
1、等边三角形三边
,三个角都等于
度.
2、等边三角开形是轴对称图形,有
条对称轴.
3、如图,已知△ABC和△BDE都是等边三角形,
求证:AE=CD
A
B
C
D
E
相等
60°
三
4、等腰三角形一腰上的高线等于腰长的一半,
则此三角形的三个角的度数分别是_________
____________________________________
30°、
75°、
75°或15°、15°、
150°
A
B
C
D
A
B
C
D
1.如图,在正△
ABC的边BC上任取一点D,以CD为边向外作正△
CDE,
求证:BE=AD。
A
B
C
D
E
如图乙,若P点在BC的延长线上,那么PD、PE和CF存在什么等式关系?写出你的猜想并加以证明.
乙
变式:
小结
我们这节课学习了哪些知识?
谈谈你的体会.
等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗?
概念
性
质
判
定
等
腰
三
角
形
等
边
三
角
形
有二条边相等
1等边对等角
2三线合一
3对称轴一条
1、等边对等角
2、三线合一
3、对称轴三条
有三条边相等
1、定义
2等角对等边
1定义
2两个角是600
3等腰三角形有一个角是600
想想看,等边三角形
有什么性质?
A
B
C
⑴三边之间
AB_AC_BC
⑵三角之间
∠A_∠B_∠C
=
=
=
=
⑵ 等边三角形的三个内角都相等,并且
每一个角都等于60°.
等边三角形的性质
⑴ 等边三角形的三边都相等
A
B
C
)
(
60°
60°
思考题
?
一个三角形满足什么条件
就是等边三角形?
一般三角形
等边三角形
⒈
三个角都相等的三角形是等边三角形.
⒉
有一个角是60°的等腰三角形是等边
三角形.
等边三角形
等腰三角形
想一想
课外活动小组在一次测量活动中,测得
∠APB=60°AP=BP=200cm,他们
便得到了一个结论:池塘最长处不小
于200cm.他们的结论对吗?
)
60°
P
A
B
如图,将两个含30°角的三角尺摆放在一起。
你能借助这个图形,找到Rt
△ABC的直角
边BC与斜边AB之间的数量关系吗?
B
A
C
D
30
°
30
°
一、动手操作、探究新知
E
A
C
B
另证:在BA上截取BE=BC,连接EC
则△BCE是等边三角形,所以
∠BEC=
60°,而∠A=
30°,
所以∠ECA=
30°,
所以AE=EC,于是有
BC=
AB
直角三角形的性质定理:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
A
C
B
在解有关直角三角形的边的关系的问题中,
常常会用到这条性质,这是一种常用的方法。
想一想:如图,在Rt△ABC中,若
则∠A为几度?
BC=
AB
A
C
B
D
下图是屋架设计图的一部分,点D是
斜梁AB的中点,立柱BC、
DE垂直于
横梁AC,AB=7.4m,∠A=30°立柱
BC
、
DE要多长?
A
B
D
E
C
解:∵DE⊥AC,
BC⊥AC,
∠A=30°
可得
2BC=AB,
2DE=AD
∴BC=1/2
×7.4=3.7m
又
AD=1/2
AB
∴DE=1/2
AD=1/2
×3.7=1.85m
答:立柱BC的长是3.7m,DE的长是
1.85m.
比一比:看
谁
算
的
快
1.如图:在Rt△ABC中
∠A=300,AB+BC=12cm
则AB=_____cm
C
B
A
300
8
2.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm, BD=___, BE=____
A
C
E
B
D
4cm
2cm
例题1.
如图在△ABC中,AB=AC=2a,∠ABC=∠ACB=150,CD是腰AB上的高,求CD的长
┏
D
C
B
A
解:∵∠ABC=∠ACB=150
∴∠DAC=∠ABC+∠ACB=300
∴CD=1/2AC=a
要把一块三角形的土地均匀分给甲
、
乙、丙三家农户去种植,如果∠C=90°∠B=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.
A
C
B
┓
请你分一分
A
B
C
D
如图,在△ABC中,∠BAC=90°,∠B=30°,AD⊥BC于D。求证:BC=4CD
如图,
∠AOB=
30°,P是角平分线上的点,
PM⊥OB于M,PN//OB交OA于N,若PM=1cm,
则PN=________.
2cm
A
N
M
P
B
O
E
一、回顾与反思
1、等边三角形三边
,三个角都等于
度.
2、等边三角开形是轴对称图形,有
条对称轴.
3、如图,已知△ABC和△BDE都是等边三角形,
求证:AE=CD
A
B
C
D
E
相等
60°
三
4、等腰三角形一腰上的高线等于腰长的一半,
则此三角形的三个角的度数分别是_________
____________________________________
30°、
75°、
75°或15°、15°、
150°
A
B
C
D
A
B
C
D
1.如图,在正△
ABC的边BC上任取一点D,以CD为边向外作正△
CDE,
求证:BE=AD。
A
B
C
D
E
如图乙,若P点在BC的延长线上,那么PD、PE和CF存在什么等式关系?写出你的猜想并加以证明.
乙
变式:
小结
我们这节课学习了哪些知识?
谈谈你的体会.
等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗?
概念
性
质
判
定
等
腰
三
角
形
等
边
三
角
形
有二条边相等
1等边对等角
2三线合一
3对称轴一条
1、等边对等角
2、三线合一
3、对称轴三条
有三条边相等
1、定义
2等角对等边
1定义
2两个角是600
3等腰三角形有一个角是600
